syi.hu/cse
Előszó
"Dr. Felix Smith, a Stanford Kutatóintézet Molekuláris Fizika Tanszékének vezetője mesélt egy fizikus barátjáról, aki Los Alamosban dolgozott a II. világháború után. Egy bonyolult probléma megoldása végett elment a híres magyar matematikushoz, Neumann Jánoshoz, aki Los Alamosban volt konzultáns.
A karakterisztikák módszerével egyszerűen meg lehet oldani. — mondta Neumann. —
Félek, nem értem a karakterisztikák módszerét. — felelte a fizikus. —
Fiatalember, — válaszolta Neumann — a matematikában az ember nem megérti a dolgokat, hanem megszokja."
[GaryZ]
☀
Több, mint két éven át írtam ezt a könyvet. Talán a legfontosabb célom az volt, hogy az érték, a norma, az érdek, a racionalitás, a racionális cselekvés fogalmait minél pontosabban definiálni, értelmezni tudjam. Azt gondoltam, hogy ezek azok az alapvető fogalmak, amelyekre támaszkodva a leginkább képesek lehetünk megmagyarázni a társadalmi cselekvések szabályszerűségeit. Mire a könyvem végére értem sok minden átértékelődött bennem e céllal kapcsolatban. Ma már úgy látom, hogy az embert leginkább az érzelmein és a szokásain keresztül érthetjük meg. Nem könnyű belátni, még nehezebb elfogadni, de én – ma már – úgy gondolom, hogy választásainkat az érzelmeink és szokásaink, illetve a mindezek mögött álló belső, nem tudatosan kezelt késztetéseink határozzák meg. Ha meg akarjuk érteni magunkat, döntéseinket, cselekvéseinket, akkor bizony mindezek kihagyhatatlanok, tehát módszeresen fel kell tárnunk az érzelmeink, késztetéseink működését, hatásmechanizmusait. De talán még ennél is fontosabb ténye az életünknek, hogy a cselekvéseink igen nagy részét (amit csak lehet) szokásokká, reflexekké alakítjuk (habituáljuk), és ezek után, illetve ezek alapján sok esetben "egyszerű" cselekvésautomataként működünk. Ingereket, inputokat kapunk, és ezekre reflexszerűen válaszolunk. Sokkoló élmény volt ráébredni arra, amire két híres ember, Neumann János és Alfred North Whitehead (☜) mondatai utalnak: még a racionális működésmódunk is – jelentős részben – megszokáson alapul. Az agyunk számára így gazdaságos, tehát metaszinten, evolúciós értelemben mindez racionálisnak mondható, de akkor is nehezen emészthető. Ez az elmozdulás még nem igazán érezhető a könyvemben. [♦] Amíg írtam, mindvégig az eredeti célok – ha tetszik, a racionalitás paradigma – mentén haladtam. Mindazt, amit itt megírtam, szükségesnek gondolom a társadalmi cselekvések szabályszerűségeinek magyarázatához. Szükségesnek, de messze nem elégségesnek. Ma már úgy látom, hogy sokkal kisebb – vagy legalábbis más – szerepe van az életünkben a racionalitásnak, a mérlegelésnek, a kalkulációnak, mint ahogy korábban hittük, hittem. De legalább van mit újragondolni, újraértelmezni, feltárni, megérteni.☁
Amikor szociológushallgatóként először kellett Max Weber munkáit olvasnom, bár éreztem, mennyire fontos szerző, sokáig nem igazán értettem. Sokat küzdöttem azért, hogy befogadjam a gondolatait. Volt, hogy oldalakon át szóról szóra leírtam egy papírra a meghatározásait, hogy jobban megérthessem azokat. Aztán szép lassan bigott Weber hívővé váltam. Úgy vélem, hogy a weberi kategóriatan a mai napig a legpontosabb fogalomkészletet nyújtja az emberi cselekvés értelmezéséhez. Van, ahol pontosítani érdemes, van, ahol ki kell egészíteni, de a szerkezet egésze ma is szilárdan áll [SyiWe] Mindez kiderül a könyvemből is, mégcsak figyelmes olvasónak sem kell lenni hozzá. Nem is akarom ezt letagadni. Könyvem egyfajta tisztelgés egy nagy ember munkássága előtt.☂
Amikor a könyvem témáihoz kerestem tanulmányokat, könyveket az elmúlt években, hol megdöbbenve, hol irigykedve, egyik ámulatból a másikba esve szembesültem azzal, hogy milyen fontos felismeréseket, eredményeket produkáltak a kognitív tudomány, biológia, agykutatás, pszichológia metszetében dolgozó kutatók. Ma már nem mernék belekezdeni a könyvembe anélkül, hogy ne építsem bele a mondandómba a lehető legnagyobb mértékben ezt a tudást. A társadalomtudományi gondolkodást legfontosabb kérdéseit illetően van, amit más megvilágításba helyez, van, amit megerősít és bizonyos értelemben megalapoz.☃
A könyv (különösen a könyv bizonyos részeinek) megírásakor egy nagyon is gyakorlati cél lebegett a szemem előtt. Kezdetektől fogva úgy gondoltam, hogy a formális imperszonális deontika kidolgozásától talán azt remélhetjük, hogy valamiféle kiindulási pontot, logikai alapot képes nyújtani egy jogi szemantika, jogi ontológia kidolgozásához, ami valamikor majd a normatív, elsősorban persze a jogi szövegek gépi feldolgozását teszi lehetővé. Idővel kiderült, hogy más fejezeteket is meg lehet úgy írni, hogy a természetes nyelvű szövegfolyamba beillesztem az alapfogalmak formális meghatározásait is, hogy egy valamikori gépi elemzés számára fogódzókat tudjak kínálni. Tudtam, hogy ezzel saját szövegem olvashatóságát nehezítem, de ezt kisebb veszteségnek éreztem a potenciális előnyökhöz képest. Arra is gondoltam, mi van, ha nem csak a társadalomtudományra, de a tudomány egészére igaz az idézett tézis, és egyetlen tudomány van. Nem előzetes tudatos döntés, inkább sodródó építkezés eredménye volt, hogy a könyvet a későbbi elemzéshez szükséges logikai alapok bemutatásával kezdem. Ahogy írtam az egyes fejezeteket, újabb és újabb logikai apparátus használatára volt szükségem, és ezek rövid összefoglalását mindig a könyv elejére tettem, míg egy önálló fejezet nem lett belőlük. Ebben a részben nem nagyon van újdonság, viszont az itt leírtak szükségesek a későbbi mondanivaló kifejtéséhez és befogadásához.☄
A könyv nagy részét a Normák, közös tudás, kooperáció című (OTKA K83887) kutatás során írtam meg. Köszönöm mindazok támogatását, akik bizalmat szavaztak a projektnek, és köszönöm azok segítségét is, akik velem együtt részt vettek ebben a kutatásban.Logikai alapok
" … » a matematika egyik fegfontosabb hozzájárulása a tudományos problémák megoldásához az lehet, hogy az adott problémával kapcsolatban a logikailag létező lehetőségek kimerítő elemzését adja«. Egy ilyen elemzés eredménye a logikailag létező lehetőségek halmazának felosztása egymást kölcsönösen kizáró, de együttesen kimerítő alternatívákra." (idézet Kemeny, Snell és Thompson könyvéből [LarsL]
Ebben a fejezetben bemutatom, értelmezem azokat a módszertani, logikai fogalmakat és elméleteket, amelyeket használni fogok a cselekvéselmélet felépítése során. Nem az a célom ezzel a fejezettel, hogy kimerítő és minden szempontból megalapozott logikai ismereteket adjak át az olvasónak. Csak azt szeretném, hogy egyfelől a könyvem gondolatmenete kellő mértékben megalapozott legyen, másfelől akik birtokában vannak az itt használt logikai apparátusoknak, azok tudják kötni ezeket a fogalmakat az általuk már ismert szerzőkhöz, diszciplinákhoz, akik számára pedig mindezek újdonságot jelentenek, azok tudják, hová kell fordulniuk, ha mélyebb tudásra vágynak. [♦] A logika eszköz ahhoz, hogy a gondolatainkat következetes és egyértelmű módon fejezhessük ki. Az egyértelműség és ezzel a – relatív – konzisztencia lehetősége abból fakad, hogy az elméleteink fogalmait valamilyen formális nyelven, formulák segítségével is reprezentálni tudjuk. Ez azonban nem jelenti azt, hogy csak formulákon keresztül fejtenénk ki mondanivalónkat. A tudományos kommunikációban lényegszerűen két nyelvet használunk. Az emberhez természetes nyelven szólunk, az elméleteinkhez használt formális nyelv(ek) mindig csak kiegészítik a természetes nyelvű kommunikációt. De ha szükséges, az egyértelműsítés kedvéért a formális nyelvekhez fordulhatunk. További előnye lehet még a logika (matematika) alkalmazásának az a "megnyugtató" érzés, amely akkor keletkezhet bennünk, amikor választ várunk arra a kérdésre, vajon az éppen adott elmélet építése közben lehetne-e más irányban továbbmenni, más fogalmakat használni, más téziseket keresni. A tudományos gondolkodás versenyében mondanak ezt, mondanak azt, és mindig ott lapul a kérdés, nem lehet-e még további fogalmakat, állításokat, elméleteket az addigiak mellé tenni. A fejezet mottájában idézett gondolat arról szól, hogy miután már elköteleztük magunkat bizonyos fogalmak, axiómák, tézisek, elméletek mellett, utána már gyakran kerülhetünk olyan helyzetbe, amikor a logika, matematika összefüggéseire támaszkodva mondhatunk olyat, hogy ennyi és ennyi, ez és ez a lehetőség van elméletileg, megvizsgálhatjuk az összeset, és abban az értelemben megnyugodhatunk, hogy azon a ponton további alternatívákat már nem kell, mert nem is lehet keresnünk. Az egyértelműség és a konzisztencia kialakításának és fenntartásának lehetőségén túl van még egy érv a logikai apparátus alkalmazása mellett. Egyfajta takarékossági, gazdaságossági szempontból is gondolhatunk a logikára, amikoris az elméletépítéseink során újra és újra alkalmazzuk a logika különböző következtetési szabályait, kalkulusait, szillogizmusait. A következtetési szabályok folyamatos alkalmazása (újrahasznosítása) nagyon fontos hozadéka a logikának. [♦] A gazdaságossági szempontokat azonban nem minden áron érdemes/lehet figyelembe venni. A rokonsági fogalmak (apja, anyja, fia, lánya, testvére, húga, nagyapja, ükapja, sógora, ángya stb.) többszáz tételből álló rendszerét kifejezhetnénk 5-6 alapfogalom segítségével, de nem tesszük ezt [♦] Terminológiai szempontból gazdaságos lenne, hiszen a többszáz helyett csak néhány terminust kellene felvenni a modellünkbe, viszont ennek az lenne az ára, hogy hosszú kifejezéseket kellene képeznünk az alapterminusainkból. 'Ükapád' helyett az 'apád apja apjának apja' alakot (formulát) kellene mondanunk. Ez se kimondani, se befogadni nem lenne jó. Állandóan dolgozni kellene azon, hogy az adott kifejezés mit is jelent. Nekünk, embereknek könnyebb sok terminust és kevesebb feldolgozási műveletet kezelnünk, mint fordítva. Érdemes hallgatnunk Whitehead fenti – az előszó mottójába foglalt – figyelmeztetésére. A logika egyfelől nagy hagyományokkal bíró, önálló tudományág. Ebben a minőségében behatárolható, közös vizsgálati tárggyal, sajátos elemzési szempontokkal, módszerekkel rendelkezik. Másfelől logikának mondhatunk minden formális nyelven kifejezett elméletet is. A kommunikálni kívánt fogalmakat az adott nyelvnek megfelelő terminusok (nevek és predikátumok) segítségével fejezzük ki, ezek révén kijelentéseket (mondatokat, formulákat) képzünk, melyekhez aztán igazságértékeket rendelünk, miközben figyelembe vesszük a nyelvhez kapcsolható szintaktikai szabályok összességét. Mindezt azért csináljuk, hogy a terminusainkkal, mondatainkkal szemantikalag (tehát jelentésüket tekintve) is megfelelő üzeneteket hozhassunk létre. Ebben az értelemben sokféle logikát hozhatunk létre, melyeket aztán különféle szempontok alapján természetesen tipizálhatunk, ezáltal "korlátozhatjuk" a használatba vehető logikák számosságát. Minden logika számára fontos a logikai kalkulus (röviden: kalkulus) fogalma. A kalkulus azon univerzális szabályok (kijelentések, formulák, tételek) összefüggő rendszere, amelyek mindig igaznak bizonyulnak, bármilyen, az adott logikai nyelvhez tartozó kijelentést (formulát), predikátumot vagy nevet helyettesítünk beléjük. A kalkulus olyan axiómarendszer, amely az adott logikai nyelv lehetséges formulái közül egyfelől leírja azokat a logikai igazságokat, amelyek tautológiák (mindig igazak), másfelől megadja azokat a szabályokat, amelyek segítségével további formulákat lehet levezetni az adott nyelven. E kettősséggel voltaképpen azt ígéri minden logika, hogy a kalkulusokra támaszkodva minden további állítást, formulát ki lehet fejezni (le lehet vezetni), ami másképp szólva azt jelenti, hogy ami az az adott nyelven "elmondható", kifejezhető, az elmondható, kifejezhető csak a kalkulusba tartozó axiómák használatával – legfeljebb nagyon bonyolult, nagyon hosszú kijelentések, formulák megfogalmazására lehet szükség. Mivel azonban ez a bonyolultság megnehezíti a nyelv – emberek általi – használatát, ezért az adott nyelven nemcsak lehet, de kívánatos is új és új formulák, terminusok bevezetése, ami logikai értelemben redundáns, praktikus szempontból viszont gazdaságos. Említettem már azt a köznapi példát, miszerint hivakozhatnánk valakire úgy is, mint az 'apám apjának az apjának az apja', illetve mint az 'ükapám', mindkétszer ugyanarra a személyre mutathatnánk rá (tekintsünk most el az apai és anyai vonal különbségétől). Ha az első megoldást választom, akkor hosszabban kell beszélnem és nehezebben lehet befogadni az üzenetet, viszont ezen a nyelven nem kell új terminust bevezetnem, megtanulnom és megtanítanom. A második megoldás gyorsabb és könnyebben folytatható kommunikációt kínál, aminek az az ára, hogy új terminust kell a nyelvbe felvenni. Ennek az a hátránya, hogy az ember számára nyilván korlátos a befogadható terminusok száma. [♦] Változik a helyzet akkor, amikor számítógépeket is bevonunk a kommunikációba, mert azok számára nem jelentkeznek ilyen feldolgozási problémák. A gépek számára sokszor elhagyható ez a terminológiai redundancia, bár azt mindig mérlegelni kell, hogy a gépek valamilyen ponton már emberekkel is kapcsolatba kerülnek is ilyenkor váltani kell az ember számára kényelmesebb, redundáns "beszédmódra". Minden logika fontos tulajdonsága a logika kifejező- vagy leíróereje, amivel azt fejezhetjük ki, hogy milyen típusú állításokat, fogalmakat tudunk megragadni az adott formális nyelv segítségével. Ez más szempontból azt jelenti, hogy a nyelv kifejezőereje attól függ, hogy az adott nyelven kifejezett elméletbe milyen ontológiai elköteleződések mentén veszünk fel új és új terminusokat (fogalmakat). Ha olyan logikánk van, amely csak mondatokat (kijelentéseket) tud kezelni, akkor tartalmilag nagyon keveset állíthatunk arról, mi van a világban, és természetesen nagyon keveset (gyakorlatilag semmit sem) tudunk elmondani arról, mit gondolunk a világról. Ha a rokonsági rendszerek világát akarjuk egy elméletben leírni, akkor fel kell vennünk pár alapfogalmat (gyereke, fiatalabb, férfi, házastársa), és ezek segítségével már minden ismert rokonsági fogalmat kifejezhetünk. Ám amíg nem vesszük be a modellünkbe a férfi kategóriáját (vagyis nem köteleződünk el az ember kettős szexuális minősége mellett), addig ugyan definiálni tudjuk a szülő, a testvér, a nagyszülő stb. fogalmait, de nem tudunk különbséget tenni az apa és anya, a fia és lánya, a húga és bátyja fogalmak között. Ez a problémakör kapcsolódik a logikai nyelv pontossága, finomsága, granularitása kérdéséhez, ami kijelöli a nyelv helyét az általánosság kontra specifikusság tengelyen. A formális nyelvekhez tartozik azok következtetési képessége: bizonyos állítások alapján a nyelv levezetési szabályai szerint további állításokat tehetünk pusztán logika eszközök segítségével. A következtető rendszer használhatóságát felülről korlátozza az igénybe vett nyelv kifejezőereje, a nyelv ontológiájának kiterjedtsége és felbontása, ami meghatározza, hogy az adott nyelv segítségével mennyire komplex összefüggések írhatóak le. Azonban minél nagyobb egy nyelv kifejezőereje, annál szűkebb az olyan kérdések köre, melyre (matematikailag) egyáltalán lehetséges a válaszadás. Így találni kell egy egészséges egyensúlyt, amelynél már kellően bonyolult összefüggéseket le tudunk írni, ugyanakkor a kérdések megválaszolhatósága még nem reménytelen. A formális nyelvek bonyolultsága, számíthatósága, eldönthetősége nagyon fontos problémakört alkot, a nyelvek használhatósága szempontjából is kiemelt kérdésnek számít, ám e könyv mondanivalója szempontjából elhagyhatónak tűnik, ezért nem tárgyalom. Az általam használni kívánt logikák egymásra épülését két dimenzióhoz igazodva lehet kifejezni. Figyelni lehet arra, hogy (i) hanyadrendű logikáról van szó, illetve (ii) extenzionális vagy intenzionális logikát vizsgálunk-e [Ruzsa] Az extenzionális logikákat úgy veszem sorba, hogy kezdem a nulladrendű propozicionális logikával, majd áttérek az elsőrendű predikátumlogikára, valamint az utóbbi alá sorolható kategoriális logika néhány kérdésére, végül röviden kifejtem, hogy hogyan lehet definálni a másodrendű (magasabbrendű) logikákat, és miért fontos figyelembe venni azt, hogy magasabbrendű logikákról (és fogalmakról) van-e szó. Az intenzionális logikák közül bemutatom a modális logikát általában, kitérek kicsit az episztemikus és doxasztikus logika, valamint a deontikus világára is, de ezeket csak azért és olyan mélységben tárgyalom, hogy érzékeltetni tudjam, milyen apparátusokat mozgatnak ezek a területek. A cselekvéselmélet tárgyalásához szükséges fogalmakat – ahol csak tudom – megpróbálom úgy bemutatni, hogy formális nyelven reprezentált terminusokkal fejezem ki a fogalom jelentését. Ezt úgy teszem, hogy megmutatom az új, éppen definiálandó fogalom helyét a már létező, addig már bemutatott fogalmi modell struktúrájában. Ezáltal – remélhetőleg – átláhatóbbá válik, hogy az éppen felvett új fogalomhoz milyen ontológiai elköteleződések szükségesek. Az egyes – jól elkülöníthető – elméleteket önálló logikákkal írom le. A cselekvéselmélet egész belül az alábbi logikákat (és a hozzájuk tartozó jelöléseket) fogom használni.| (AL.xx) | aggregációlogika (hun) | aggregation logic (eng) |
| (BA.xx) | preferenciális algebra (hun) | preferential algebra (eng) |
| (BL.xx) | preferencialogika (hun) | betterness logic (preference logic) (eng) |
| (DL.xx) | deontikus logika (hun) | deontic logic (eng) |
| (EL.xx) | episztemikus logika (hun) | epistemic logic (eng) |
| (FL.xx) | formális logika (hun) | formal logic (eng) |
| (GL.xx) | kategórialogika (hun) | category logic (eng) |
| (HL.xx) | halmazlogika (hun) | set logic (eng) |
| (IL.xx) | interakció logika (hun) | interaction logic (eng) |
| (ML.xx) | modális logika (hun) | modal logic (eng) |
| (PC.xx) | kijelentéskalkulus (hun) | propositional calculus (eng) |
| (PL.xx) | kijelentéslogika (hun) | propositional logic (eng) |
| (QL.xx) | predikátumlogika (hun) | predicate logic (eng) |
| (QC.xx) | predikátumkalkulus (hun) | predicate calculus (eng) |
| (RA.xx) | relációalgebra (hun) | relation algebra (eng) |
| (RL.xx) | relációlogika (hun) | relation logic (eng) |
| (ZL.xx) | intencionalitáslogika (hun) | intentionality logic (eng) |
Metafogalmak
A formális nyelveket mindig a természetes nyelvek analógiájára építjük fel abban az értelemben, hogy szavakat (kifejezéseket, terminusokat, fogalmakat) definálunk, amelyekkel a világban létező vagy létezőnek hitt dolgainak valamely halmazára mutatunk rá, illetve ezen szavak egymás mellé illesztésével (relációba állításával) mondatokat (kijelentéseket) állítunk elő azzal az igénnyel, hogy azokkal érvényes állításokat tegyünk a világról. [♦] Eközben észrevétlenül használunk olyan fogalmakat, amelyeket magától értetődőnek tekintünk, de nem – vagy csak ritkán – reflektálunk rá. A legfontosabbakat ezek közül bemutatom itt. A nyelvhasználat során – a dolgokat kissé elegyszerűsítve – kétfajta dolgot teszünk. Egyfelől szószerű nyelvi jeleket képzünk, hogy azokkal létező vagy tételezett dolgok halmazára rámutathassunk, referálhassunk rájuk, a dolgokat reprezentálhassuk a "szavakkal". Ezekkel a szószerű nyelvi jelekkel kevés dolgot fejezhetünk ki, amikor használjuk őket. Talán csak annyit, hogy az adott nyelvi jelet kibocsátva (leírva, kimondva) tételezzük a világ bizonyos dolgainak létezését – legalább annyira, hogy aztán kijelentéseket tehessünk róluk. Az ilyen megnyilatkozások érvényességét csak annyiban lehet vitatni, hogy magát a létezési feltételt támadhatjuk, semmi mást. Akkor tudunk tartalmasabb, mélyebb és szerteágazóbb érvényességvizsgálatba keveredni, ha mondatszerű nyelvi jeleket képzünk. Ezt úgy tehetjük meg, ha a szószerű nyelvi jeleket kapcsolatba állítjuk egymással. Ez a kapcsolatba állítás (valamilyen reláció képzése) az a művelet, amelynek révén szószerű jelekből állításokat keletkeztethetünk, ezért a reláció a mondatszerű megnyilatkozások kulcsa. Mivel a szószerű jelek egymáshoz illesztését rengetegféleképpen tehetjük meg, a mondatszerű megnyilatkozások szintjén megnő a kifejezés gazdagsága, mélysége, szélessége és vitathatósága egyaránt. Amikor egy elméletet építünk fel, akkor ezt a kettősséget kell mindvégig szem előtt tartani. A logika alapfogalma az állítás. Azt természetesen nem állítom, hogy ez a fogalom ne lenne reflektált a logika világában, de azt fontosnak tartom hangsúlyozni, hogy sokszor zavart okoz az a tény, hogy a logika nyelvek túlnyomó részében nincs önálló jele, reprezentációja ennek a fogalomnak. [♦]$\concept{PROPOSITION}\equiv A \;|\;B\;|\;C$
állítás (hun) – kijelentés (hun) – propozíció (hun) – ítélet (hun) – mondat (hun) – asszerció (hun) – affirmáció (hun) – formula (hun) – proposition (eng) – assertion (eng) – judgement (eng)
Az állítás igazságra vonatkozó érvényességigénnyel fellépő, adott nyelv szabályai szerint érvényes nyelvi megnyilatkozást kibocsátó aktus eredménye. A tényleges gyakorlatban az állítás fogalmának nincs külön jele. Az állítások logikai értéke igaz vagy hamis lehet, amit szöveges megjelenítésben 'igaz' vagy 'hamis' karakteres formák, táblázatokban a '0' és az '1' értékek feltüntetésével fejezhetünk ki. Minden nyelvben fontos a tagadás fogalma, amely az állítás "párja". Leggyakrabban olyan műveletként definálják, amely valamely állításhoz képest előállít egy újabb állítást úgy, hogy az eredeti és az új állítás logikai értéke ellentétes egymással.$\concept{NEGATION}\equiv\lnot\equiv \;\sim$
tagadás (hun) – negáció (hun) – negation (eng)
A tagadás az a logikai, nyelvi művelet, amely során valamely állítás logikai értékét ellentétére változtatjuk. A tagadás állításra irányul függetlenül attól, hogy egyszerű vagy összetett állításokról van-e szó. Az állítással, illetve annak tagadásával a mondatszerű nyelvi megnyilatkozásokat reprezentálhatjuk. Ahhoz, hogy a kijelentéseink belső tartalmát, tehát a szószerű jeleket is meg tudjuk ragadni, szükség van a terminus fogalmára. Minden szószerű nyelvi jelre, amelyekkel még nem tudunk állításokat kifejezni, ráhúzhatjuk a terminus kategóriáját. A terminussal a világ dolgaira mutatunk rá, és ezt a kapcsolatot (a terminusok és a világ között) egyfelől a terminus terjedelmébe sorolt dolgokkal, másfelől a terminus jelentésével jellemezhetjük.$\concept{TERM}\equiv a\;|\;b\;|\;c\;|\; x\;|\;y\;|\;z\;|\;\rel{P}\;|\;\rel{R}\;|\;\rel{Q}$
terminus (hun) – kifejezés (hun) – fogalom (hun) – konstrukció (hun) – term (eng) – concept (eng) – expression (eng) – construction (eng)
A terminus a világban adott vagy képzelt dolgokat vagy ilyen dolgokból álló halmazokat reprezentáló nyelvi megnyilatkozás. Ontológiai elkötelezettségeink alapvetően a terminusokkal, fogalmakkal leírt dolgokra vonatkoznak. Bár szigorú tárgyalásmód esetén a terminus, kifejezés, konstrukció kategóriáit mint a nyelvi szinthez, a fogalom kategóriáját mint a fogalmi szinthez tartozót el kell választanunk egymástól, itt megengedhetőnek tartom azt a pongyolaságot, hogy ezek együttesen mind a dolgokra irányuló kategóriára utalnak. A tagadás mellett használjuk gyakran a komplementálás fogalmát is, aminek szoros kapcsolata van ugyan a tagadás fogalmával, sokban hasonlít hozzá, de mégsem azonos vele.$\concept{COMPLEMENT}\equiv\lnot\equiv \;\sim$
komplementálás (hun) – complement (eng)
A komplementálás az a logikai művelet, amelynek során a terminus terjedelme alapján vesszük az univerzális halmazhoz képest komplementer terjedelemmel rendelkező terminust. A komplementaritás a halmazelmélet gyakran használt fogalma, és mivel valamely halmaznak az univerzumhoz képest vett kiegészítését jelenti, a komplementer halmaz képzése a tagadás műveletével mutat szoros rokonságot. Egy halmaz és annak komplementere úgy viszonyul egymáshoz, mint egy állítás a tagadásához. Előfordul, hogy a tagadás, negálás terminusait is a komplementálás értelmében alkalmazzák, és a komplementerképzés terminusa is szinoním a komplementálás terminusával, míg a komplementaritás fogalma az egész jelenségegyüttest írja le. A halmazelméletben a komplementer halmaznak (és így áttételesen a komplementálás műveletének) van saját jelölése, ez olykor felbukkan a formális nyelvekben is, de gyakrabban alkalmazzák a tagadás műveletét jelző szimbólumo(ka)t erre a műveletre. A halmazelméleti eredet és analógia rámutat arra, hogy ott lehet alkalmaznunk a komplementálás fogalmát, ahol elemekkel, előfordulásokkal, terjedelemmel van dolgunk, ez pedig a terminusok világa. A komplementálás művelete a terminusok terjedelmébe sorolt előfordulások univerzumhoz képest vett kiegészítése. A tagadás művelet viszont – elsősorban – kijelentésekre vonatkozik, ennyiben szemben áll a komplementálás fogalmával.Következtetések
Amikor egy nyelvi megnyilatkozásnak ismerjük valamilyen belső szerkezetét, akkor mindig felmerülhet az a kérdés, vajon értelmes-e, és ha igen, milyen eredményeket produkál az, ha a belső szerkezetét (vagyis az összetevők egymáshoz való viszonyát) megváltoztatjuk. A későbbi tárgyalandó elméletekben is elő-előkerülnek ilyen-olyan változtatási, transzformációs műveletek, úgyhogy röviden érdemes kitérni erre a kérdéskörre. Már csak azért is érdekesek ezek a szabályok, mert közülük több is a közvetlen következtetések vagyis az egyetlen állításból levonható következtetések körébe tartozik, és mint ilyenek a következtetési szabályok egyik fontos csoportját jelentik. Egy nyelvi megnyilatkozásnak kétféle értelemben lehet belső szerkezete. Egyfelől ha mondatszerű megnyilatkozásokat vizsgálunk, akkor a "mondatok" belső szerkezetét nem ismerhetjük, viszont elemezhetjük a mondatok összekapcsolását, amikoris az egyes mondatok mint összetevők már a megnyilatkozás mint egész részeiként, belső szerkezeti egységeiként értelmezhetők. Másfelől viszont tekinthetjük a mondatszerű megnyilatkozást (vagy csak annak egy részét) is olyan egységnek, amelynek a belső szerkezete érdekel minket, amikor a szószerű összetevőit és azok egymáshoz, illetve a mondategészhez (vagy csak a mondat egy részéhez) való viszonyát akarjuk megérteni.Jelölési konvenciók
A tudományos diskurzusban fogalmakat, tételeket, elméleteket gyártunk, és igyekszünk minél pontosabban kifejezni ezeket. Ebben nagy segítséget jelent minél több formalizmus alkalmazása. De még ha így teszünk, akkor is szavakkal kommunikálunk egymás felé, és ilyenkor mindig könnyen pongyolává válhatunk. Egyszerűen azért, mert amikor az esetleg egyértelműen formalizált fogalmainkat természetes nyelvi szinten fejezzük ki (terminusok, kifejezések, nyelvi konstrukciók alkalmazásával), folyamatosan belebonyolódunk a szinonimitás és homonimitás hálójába. Még a tudományos kommunikációban is tele vagyunk hononím és szinoním szavakkal, kifejezésekkel. Ezen a nehézségen azzal próbálok felülkerekedni, hogy amikor egy-egy új fogalmat vezetek be, akkor mindig megadom azt, hogy hogyan hivatkozom rá fogalomként, illetve hogyan hivatkoznak rá a különböző tudományterületek képviselői, a különböző szerzők természetes nyelvi konstrukciókkal. A magyar mellett igyekszem mindenhol angol nyelvű konstrukciókat is megadni. A fogalmakat kisebb méretű, verzál betűtípussal jelzem, és ilyenkor gyakran rövidítéseket vagy angol nyelvű terminusokatt használok. A fogalmi síkon megpróbálom teljesen kizárni a homonimitás lehetőségét, és bár ezen a szinten lehetségesnek vélem a szinonimitás jelenségét, de igyekszem ezeket is elkerülni. A természetes nyelvi konstrukciók, terminusok jelölésére – első és/vagy lényeges felbukkanásuk során – vastagított, talpatlan betűt használok. A konstrukciók szintjén mind a homonimitás, mind a szinonimitás jelensége gyakran előfordul. A logikai formalizmusokkal támogatott modellépítés egyik fontos célja pont az, hogy ahol csak lehetséges, meg lehessen találni az olyan helyzeteket, amelyekben a tudományos kommunikáció során szinoním vagy homoním terminusokat használunk. Amikor a terminusok, konstrukciók szintjén az egyértelműsítés miatt ez szükségesnek látszik, akkor zárójelben megadom, hogy az adott konstrukció melyik fogalomhoz kapcsolódik. Ezt természetesen akkor teszem csak meg, amikor egy-egy új terminust (fogalmat) bevezetek a modell tárgyalásakor, illetve amikor a szövegkörnyezetből nem derül ki egyértelműen, hogy az éppen használt kifejezés melyik jelentéséről van szó. Minden nyelvhez tartoznak központozást segítő jelek, amelyeket nem tüntetünk fel a nyelv definiálásakor, de mindvégig használjuk őket. Ilyenek a nyitó és csukó zárójelek ('(' és ')'), valamint az elemek felsorolását segítő vessző ',' jele. Ugyancsak "univerzálisan", azaz minden nyelvben használok két ekvivalenciajelet. Egyfelől egy-egy új fogalom bevezetésekor a definiálás jelzésére alkalmazom a '$\defi$', illetve a $\modefi$ definíciós ekvivalencia műveletjeleit attól függően, hogy tárgynyelven vagy a tárgynyelv és metanyelv közötti kapcsolatban bevezetett új elemtől van-e szó. Másfelől a terminusok szintjén létező szinonimitás kezelésére használom a '$\equiv$' terminológiai ekvivalencia művelet(jel)ét, amit megkülönböztetek a logikai ekvivalencia mondatkapcsoló operátortól. Előbbit mindig az egyazon fogalmat jelölő terminusok közti ekvivalencia, utóbbit a fogalmak definíciójában előforduló állítások közti logikai ekvivalencia jelzésére használom (tisztában vagyok vele, hogy ez megkülönböztetés logikailag kissé pongyola).Halmazelmélet
A halmazoknak, a halmazelméletnek kardinális szerepe van minden formális elméletben. Nincs szükség itt a halmazelmélet tárgyalására, de arra igen, hogy felsoroljam azokat a legfontosabb halmazelméleti fogalmakat (illetve ezek jeleit), amelyeket a könyvben mindvégig használni fogok.$\mathscr{L}_{HL}$($\mathbb{X}, \mathcal{P}(\mathbb{X}), \emptyset, \mathbb{U}, \mathbb{N}, \mathscr{R}, \{a,b,c\}, \in, =, |\mathbb{X}|, \cup, \cap, \overline{\mathbb{X}}, \setminus, \subset, \subseteq)$
| $\mathbb{X}$ | tetszőleges halmaz |
| $\mathcal{P}(\mathbb{X})$ | $\mathbb{X}$ hatványhalmaz ($\mathbb{X}$ részhalmazainak halmaza) |
| $\emptyset$ | üres halmaz |
| $\mathbb{U}$ | univerzális (teljes) halmaz |
| $\mathbb{N} (\mathbb{N}^{+})$ | természetes számok halmaza (nullával együtt vagy nulla nélkül) |
| $\mathscr{R}$ | valós számok halmaza |
| $\{a,b,c\}$ | halmaz elemei |
| $\in$ | eleme reláció |
| $=$ | egyenlőség reláció |
| $|\mathbb{X}|$ | halmaz számossága (kardinalitása) függvény |
| $\cup$ | unióképzés halmazművelet |
| $\cap$ | metszetképzés halmazművelet |
| $\overline{\mathbb{X}}$ | komplementerképzés halmazművelet |
| $\setminus$ | különbségképzés halmazművelet |
| $\subset$ | valódi részhalmaza reláció |
| $\subseteq$ | részhalmaza reláció |
$\concept{PARTITION}(\mathbb{X})\defi$ $[\forall i\in \mathbb{N}(\mathbb{S}_i\subset\mathbb{X}) \land \mathbb{S}_i\in\mathcal{P}(\mathbb{X}))] \land$ $[\emptyset \notin \mathcal{P}(\mathbb{X})] \land$ $[\bigcup\limits _{\mathbb{S}_i\in \mathcal{P}} \mathbb{S}_i = \mathbb{X}] \land$ $[\forall i\forall{j}((\mathbb{S}_i,\mathbb{S}_j\in\mathcal{P}(\mathbb{X}) \land \mathbb{S}_i\ne \mathbb{S}_j)\to \mathbb{S}_i\cap \mathbb{S}_j=\emptyset)]$
partíció (hun) – partition (eng)
A fenti formulák segítségével biztosíthatjuk, hogy az ($\mathbb{X}$) halmaz olyan részhalmazokra legyen felosztva, amelyek egymástól teljesen elkülönülnek, viszont együttesen kiadják az egész halmazt. Ez a fogalom azért fontos, mert a megfelelő particionálás a megalapozott fogalmi gondolkodás egyik legfontosabb biztosítéka (☜) A későbbiekben erre a kijelentésemre még visszatérek.Kijelentéslogika
A logikai elméletek közül elsőként a nulladrendű extenzionális logikát veszem elő [Ruzsa] A későbbiekben inkább kijelentéslogikaként fogok hivatkozni rá, de ebben a könyvben szinonímaként kezelem még az 'állításlogika', illetve a 'propozicionális logika' terminusokat is. A kijelentéslogika a mondatszerű nyelvi megnyilatkozásokra fókuszál azáltal, hogy a mondatokba foglalt elemi állítások egymáshoz fűzésének lehetőségeit, szabályait vizsgálja. Ebből következően a kijelentések belsejével, összetevőivel, vagyis a szószerű nyelvi megnyilatkozásokkal nem foglalkozik. A kijelentéslogika lényegét a kijelentéseket összekapcsoló logikai műveletek adják, ezért először ezeket kell felvenni a fogalmi modellünkbe. A következő fejezetben ezeket veszem sorba. Előtte azonban rögzítenem kell azt, milyen nyelvre van mindehhez szükség.$\mathscr{L}_{PL}(A,B,C, \lnot, \to)$
| $A,B,C$ | propozíció (formula) |
| $\lnot$ | tagadás logikai művelet |
| $\to$ | kondicionális logikai művelet |
Kijelentéslogikai műveletek
Amennyiben veszünk állításokat, és ezeket valamilyen művelet segítségével összekapcsoljuk, akkor egy újabb kijelentéshez jutunk. A kijelentéslogika azt vizsgálja, hogy ezeknek az új állításoknak milyen lesz az igazságértéke. A modellünkbe fel kell vennünk a logikai művelet fogalmát, [♦] (☜) ami kijelentések, állítások összekapcsolására vonatkozik. Mivel a fogalom nagyon széles körben használt, rengeteg szinonimája termelődött ki.logikai művelet (hun) – funktor (hun) – junktor (hun) – logikai kapcsoló (hun) – logikai konnektívum (hun) – konnektívum (hun) – mondatoperátor (hun) – propozicionális kapcsoló (hun) – mondatkapcsoló (hun) – propozicionális operátor (hun) – logical operation (eng) – logical connective (eng)
A kijelentéslogikában a műveletek változóit, összetevőit, operandusait az ítéletek alkotják. Ha nem okoz zavart, akkor az ítéletekre mint a műveletek változóira operandusként fogok hivatkozni. Ha a kijelentéslogikában igazából csak azt vizsgálhatjuk, hogy milyen módon lehet összekapcsolni a kijelentéseket, és ezekben az összekapcsolásokban milyen szabályszerűségeket találhatunk, akkor kiemelt kérdés, hogy hányféleképpen és hogyan kapcsolhatjuk össze a kijelentéseket egymással. A válasz részben függ attól, hogy milyen típusú műveletről is beszélünk. Nulláris, azaz nullaváltozós műveletből kettő, unáris, azaz (tisztán) egyváltozós műveletből négy, míg bináris, azaz (tisztán) kétváltozós műveletből tíz van (viszont mondhatjuk azt is, hogy a többargumentumú műveletek magukba foglalják a kevesebb számú változóval rendelkezőket, így hat unáris és tizenhat bináris művelet létezik). A két nulláris művelet, a tautológia és az ellentmondás jellemzője az, hogy igazságértékük független az általuk összekapcsolt állítások igazságértékeitől. A tautológia mindig igaz, az ellentmondás mindig hamis. Ezért is nevezzük nullaváltozós műveletnek őket, mivel "érzéketlenek" a bennük levő kijelentések mint változók értékeire. Az unáris műveletek értelmezésekor gyakran mondják azt, hogy a két nulláris művelet, a tautológia és az ellentmondás mellett ide tartozik még az állítás, a tagadás. A tagadásról természetesen lehet azt mondani, hogy az egy unáris művelet, aminek a bemenete egy állítás, és a kimenete egy – az állítással ellentétes igazságértékű – másik állítás. Mindig szem előtt kell azonban tartanunk azt a tényt, hogy a tagadás műveletét tetszőleges – tehát bármilyen összetettségű – állításra lehet vonatkoztatni. Beszélhetünk műveletek által előállított, összetett kijelentések tagadásáról is. A tagadás mindig egyváltozós művelet, de ettől még lehet többargumentumú. Ugyanaz igaz az állításra is természetesen, csak sokkal kevésbé tűnik intuitívnek azt mondani, hogy az állítás maga unáris művelet. Emiatt a fogalmi "kavarodás" miatt én ezen a ponton a 'projekció', illetve ennek tagadásaként a kontraprojekció fogalmát alkalmazom. A projekció olyan kétargumentumú, de egyváltozós művelet, amely a két argumentum közül csak az egyik értékeit veszi figyelembe, tehát csak attól az egy – projektált – változótól függ. A műveletek jellemzésekor bemutatom azokat a logikai jeleket, amelyeket valami-lyen formális logikai nyelvben elterjedt módon használnak, azokat a – magyar – természetes nyelvű szavakat, kifejezéseket, amelyeket a fontosabb elméletekben gyakrabban felbukkantak, megmutatom az adott művelet ellentétét, valamint megadok néhányat a műveletet jelző szimbólumok közül. Végül minden leírás mellett feltüntetek egy ábrát, ami a műveleti igazságtábla geometriai reprezentációjának tekinthető Minden művelet esetében igaz, hogy a különböző logikai nyelveken olykor más műveleti jeleket alkalmaztak, ezért még itt is, a formális nyelvek világában is létezik a szinonimitás jelensége (sőt, a homonimitás is megfigyelhető, mert elő-előfordul, hogy ugyanazokat a logikai jelekkel más műveleteket reprezentálnak). Még gyakoribb azonban a szinonimitás (és homonimitás) előfordulása a formális elméleteket körbevevő, azokat interpretáló természetes nyelvek területén (főként, ha ide soroljuk a különböző természetes nyelvek által használt terminusrétegeket is). A különböző kontextusokban kitermelődő alternativitás, illetve stilisztikai kényszerek miatt igencsak kiterjedt szinonimitással (homonimitással) kell együtt élnünk. A műveletekre vonatkozóan sokféle megnevezés verseng egymással, különböző kontextusokban más és más terminusokat használnak ugyanarra a műveletre. Amikor döntenem kellett, ezek közül melyiket válasszam magam számára, akkor azt a szempontot vettem figyelembe, hogy a megnevezések önmagukban is minél jobban utaljanak a köztük levő kapcsolatokra. Ezért – ahol csak lehetett – az egymásból származtatható műveletek esetében azokat a neveket válaszottam, amelyek utaltak két művelet közti konverziós kapcsolatra vagy a köztük levő tagadási viszonyra. Előbbit a 'retro', utóbbit a 'kontra' előtag használata jelzi. Nem lehettem azonban teljesen következetes ezen a téren, mert bizonyos relációk esetében a széles körben használt terminusokat nem lehetett nem figyelembe venni. Ilyen esetekben "önkényesen" választottam a versengő nevek közül. A tizenhat bináris logikai műveletet úgy mutatom be egymás után, hogy megadom a cselekvéselméleti modellben használt nevüket, a gyakran használt megnevezéseiket, valamit adok egy rövid szöveges jellemzést is rájuk. Megmutatom azt is, hogy miként lehet őket definálni más műveletek segítségével, de itt nem törekszem arra, hogy ugyanazt a logikai definíciót adjam meg, amivel a kijelentéskalkulusban meghatározhatjuk őket. A cél itt az, hogy értelmezni lehessen az egyes műveleteket. Akkor hát, vegyük sorba őket!$\concept{CONTRADICTION}\equiv\bot \defi A \land \lnot A$
ellentmondás (hun) – kontradikció (hun) – sosem igaz (hun) – falsum (lat) – contradiction (eng)
Az ellentmondás művelete egyfajta konzisztenciát biztosít a kijelentéseinknek abban az értelemben, hogy létével jelzi és kizárja az egymást tagadó kijelentések együttes fennállását. Mondhatjuk azt is, hogy 'Esik az eső.' és azt is, hogy 'Nem esik az eső.', de ha a kettőt egyszerre állítjuk, akkor ellentmondáshoz jutunk. Az ellentmondás művelete mint két – egymást tagadó – állítás összekapcsolása sosem lehet igaz. Ez a művelet nulláris, konstans.$\concept{CONEGATION}\equiv \;\not\lor \;\equiv \;\downarrow \;\equiv \;\nabla \;\equiv \;\mid\mid\;\defi\lnot A \land \lnot B$
konnegáció (hun) – sem-sem (hun) – NOR (log) – not OR (log) – Webb-művelet (hun) – egyesített tagadás (hun) – conegation (eng) – Webb-operation (eng)
A konnegáció a diszjunkció tagadása. Ha a hétköznapi nyelvben is használatos 'sem-sem' formulát nézzük (Sem utóda, sem boldog őse.), ezen az alakon látszik csak igazán, hogy ez a művelet "közel áll" az ellentmondáshoz, hiszen igazságtáblázataik csak egyetlen esetben térnek el egymástól: amikor mindkét operandus hamis, akkor a konnegáció igaz, míg a kontradikció hamis. Ez egyfajta szimmetricitást kölcsönöz a műveletnek. Az ellentmondáshoz való "közelség" azonban kicsit látszólagos – abban az értelemben legalábbis, hogy a művelet két összetevőjének együttes hamissága a logikai univerzum jóval nagyobb részét fedi le, mint az összes többi opció.$\concept{RETROSUBTRACTION}\equiv \;\nleftarrow\;\defi\lnot A \land B$
retroszubtrakció (hun) – konverz szubtrakció (hun) – konverz nem-implikáció (hun) – retrosubtraction (eng) – converse subtraction (eng)
Ez a művelet a szubtrakció megfordítása, konverze. A művelet jellemzésére ugyanazok mondhatók el, mint a szubtrakció esetében, a különbség csak a két operandus közti viszony irányultságában van.$\concept{CONTRAPROJECTION}\equiv \;\not\triangleleft \; \defi\lnot A$
kontraprojekció (hun) – contraprojection (eng)
Ez a művelet a projekció ellentéte, tartamilag megegyezik az A operandusba foglalt kijelentés tagadásával. Azért nevezem kontraprojekciónak, mert a kontra előtaggal valaminek az ellentétét szokás kifejezni, és ebben az esetben pont erről, a projekció tagadásáról van szó.$\concept{SUBTRACTION}\equiv\; \nrightarrow\;\defi A \land \lnot B$
szubtrakció (hun) – kivonás (hun) – nem-kondicionális (hun) – abjunkció (hun) – subtraction (eng) – abjunction (eng) – non-conditional (eng)
A szubtrakció a kondicionális művelet tagadása, amely csak akkor igaz, amikor A "önmagában" igaz, vagyis amikor B nem igaz, de A igaz. Ez utóbbi összefüggés magyarázza a "kivonás" megnevezést, hiszen a művelet igazságtartományát úgy kapjuk meg, ha A igazságtartományából kivonjuk B igazságtartományát.$\concept{CONTRA-RETROPROJECTION}\equiv \;\not\triangleright\;\defi\lnot B$
kontra-retroprojekció (hun) – contra-retroprojection (eng)
Ez a művelet a retroprojekció ellentéte, tartamilag megegyezik a B operandus tagadásával.$\concept{BISUBTRACTION}\equiv\; \nleftrightarrow\;\equiv\; \oplus\;\equiv \veebar\defi\lnot(A \leftrightarrow B)\equiv(A \land \lnot B) \lor (\lnot A \land B)$
biszubtrakció (hun) – exkluzív diszjunkció (hun) – kizáró diszjunkció (hun) – erős diszjunkció (hun) – exkluzív OR (log) – XOR (log) – vagy-vagy (hun) – kizáró vagy (hun) – kontravalencia (hun) – antivalencia (hun) – kontradiktórius (hun) – bisubtraction (eng) – strong disjunction (eng) – contravalence (eng) – antivalence (eng)
A biszubtrakció művelete a bikondicionális tagadása, de tartalmilag kapcsolatba hozható a diszjunkció műveletével is, amit félreérthetetlenül jelez több névváltozata is. Tételezhető még a szubtrakció és annak konverze, a retroszubtrakció diszjunkciójaként is. A művelet legfontosabb tulajdonsága az, hogy csak akkor igaz, ha a két operandus közül valamelyik igaz, de úgy, hogy egyszerre sosem lehetnek igazak. Ezt fejezi ki a kizáró vagy exkluzív diszjukció megnevezés. A mindennapi beszédben is gyakran használjuk ezt a műveletet. Gondoljunk csak a "csak egy maradhat", a "pénzt vagy életet" vagy a "mindent vagy semmit" szófordulatok felbukkanására. A művelet költői leírása pedig: Vagy bolondok vagyunk s elveszünk egy szálig, vagy ez a mi hitünk valóságra válik.$\concept{EXCLUSION}\equiv \;\not\land\;\equiv\; \uparrow\;\equiv\; \mid\;\equiv\; \mid\mid\;\defi\lnot A \lor \lnot B$
exklúzió (hun) – kizárás (hun) – NAND (log) – not AND (log) – nem-és (hun) – Sheffer-művelet (hun) – vagylagos tagadás (hun) – alternatív tagadás (hun) – kontrárius (hun) – exclusion (eng) – Sheffer-operation (eng)
Az exklúzió a konjunkció tagadása. Bizonyos értelemben ez a művelet van legközelebb a tautológiához, hiszen csak a két operandus egyidejű igazsága esetén hamis, minden más esetben igaz. A két összetevő, A és B együttes fennállása erős feltételt jelent, és amikor ez nem teljesül, tehát az esetek nagyobb részében, a művelet igaz. Lehet valami barna, lehet zöld, lehet egyik sem, de egyszerre nem lehet barna is, zöld is.$\concept{CONJUNCTION}\equiv\;\land \;\equiv\; \& \;\defi A \land B$
konjunkció (hun) – AND (log) – és (hun) – conjunction (eng)
A konjunkció abban az értelemben erős állítás (legalábbis a diszjunkcióhoz képest), hogy a művelet igazsága egyszerre függ a két operandus igazságától, vagyis ha fennáll a konjunkció igazsága, akkor tudhatjuk azt is, hogy ez annak "köszönhető", hogy mindkét operandus egyszerre igaz. A művelet által lefedett esetek tartománya kisebb, de az így kifejezett tudásunk "tartalmasabb", hiszen kér dolgot is tudunk (A és B igazságát). Ez az operáció is a széleskörben használt műveletek közé tartozik.$\concept{BICONDITIONAL}\equiv\; \leftrightarrow\;\equiv\; \Leftrightarrow\;\equiv{`}\equiv{'} \defi A \leftrightarrow B\equiv(A \land \lnot B) \lor (\lnot A \land B)$
bikondicionális (hun) – ekvivalencia (hun) – materiális ekvivalencia (hun) – biimplikáció (hun) – XNOR (log) – akkor és csak akkor (hun) – csakkor (hun) – a.cs.a (hun) – iff (log) – biconditional (eng) – equivalence (eng) – material equivalence (eng) – biimplication (eng)
A bikondicionális művelete a kondicionális és annak konverze, a retrokondicionális egyidejű fennállását jelenti, azaz az implikatív jelleg mindkét irányban érvényes. Fontos művelet a tudományos gondolkodás számára, de a hétköznapi kommunikációban is gyakran előfordul. Példa lehet rá a következő idézet: "A garancia akkor és csak akkor érvényes, amennyiben a terméket az adott termékre vonatkozóan jóváhagyott és a használati útmutatóban feltüntetett környezetben használják."$\concept{RETROPROJECTION}\equiv \triangleright\defi B$
retroprojekció (hun) – második projekció (hun) – jobb projekció (hun) – right projection (eng)
A retroprojekció csak annyiban tér el a projekciótól, hogy a két operandus közül nem a bal-, hanem a "jobboldalit" emeli ki, vagyis A és B közül B-t tételezi, míg A "állításától" eltekint. Ebben az értelemben a két műveletet egymás konverzeiként értelmezhetjük. A 'retroprojekció' megnevezés analóg a retrokondicionális név képzésével: a 'retro' és a 'kondicionális' szavak összetételében az előtaggal a megfordítást, a konverzitást fejezzük ki, amit – értelemszerűen – az utótagra vonatkoztatunk. A retroprojekció tartalmilag megegyezik a jobboldali operandus (vagyis B) "egyedüli" állításával.$\concept{CONDITIONAL}\equiv \;\rightarrow\;\equiv\; \supset\;\equiv\; \Rightarrow\;\defi\lnot A \lor B$
kondicionális (hun) – materiális kondicionális (hun) – implikáció (hun) – materiális implikáció (hun) – ha, akkor (hun) – szubaltern (hun) – conditional (eng) – implication (eng) – material implication (eng) – if, then (eng)
A kondicionális a hétköznapi kommunikáció talán legfontosabb művelete. Az indoklásainkban, magyarázatainkban gyakran használjuk ezt a műveletet, amely a hipotetikus állítások mintázatát adja. A hétköznapi praxis nem igazán reflektál arra a filozófiai problémára, amely abból fakad, hogy A hamissága esetén a művelet mindig igaz eredményt ad.$\concept{PROJECTION}\equiv \triangleleft\defi A$
projekció (hun) – első projekció (hun) – balprojekció (hun) – projection (eng) – left projection(eng)
Ritkán szokták a projekció műveletét ebben a kontextusban használni, helyette valamelyik operandus mint állítás tételezését alkalmazzák – miközben ezt a tételezést unáris műveletként értelmezik. Ez természetesen sok szempontból elfogadható, azonban bináris műveletek teljeskörű bemutatásakor jobbnak tartom azt a megoldást, amikor nem emelünk be unáris műveleteket az elemzésünkbe, csak bináris műveletekkel foglalkozunk. A projekció az a művelet, amely két operandus közül kiemeli az egyiket úgy, hogy a művelet igazságértékei minden ponton megegyeznek a kiemelt állítás igazságértékeivel. Ez természetesen azt is jelenti, hogy a másik operandust ilyenkor nem vesszük figyelembe, úgy tételezzük, mintha nem is létezne, nem is állítanánk. [♦] (☜) Amennyiben a bal oldali állítást (tehát A-t) projektáljuk, akkor "egyszerű" projekcióról beszélünk. Ez tartalmilag megegyezik a bal oldali propozíció tételezésével.$\concept{RETROCONDITIONAL}\equiv \;\leftarrow\;\equiv\; \subset\;\equiv\; \Leftarrow\;\defi A \lor \lnot B$
retrokondicionális (hun) – konverz kondicionális (hun) – konverz implikáció (hun) – retroconditional (eng) – converse conditional (eng) – converse implication (eng)
Ez a kondicionális művelet konverze. Tartamilag, formailag mindenben hasonlatos a kondicionálisra, csak éppen minden fordítva, "jobbról-balra van". A megszokás (vélhetőleg a balról-jobbra olvasás dominanciája) miatt a kondicionálist érezzük természetesnek. Enek ellenére a hétköznapi beszédben is előfordul. Példa rá a következő két kifejezés: Kétszer ad, ki gyorsan ad., illetve Akkor szép az erdő, mikor zöld.$\concept{DISJUNCTION}\equiv \lor \defi A \lor B$
diszjunkció (hun) – OR (log) – vagy (hun) – alternáció (hun) – megengedő vagy (hun) – gyenge diszjunkció (hun) – inkluzív diszjunkció (hun) – disjunction (eng) – alternation (eng) – inclusive disjunction (eng)s
A diszjunkció "gyenge" művelet, amely két állítást úgy kapcsol össze, hogy a művelet igazsága fennállásához "elegendőnek tartja" az egyik operandus igazságát. Abban az értelemben kell ezt gyengének tartanunk, hogy a művelet eredményeként nem tudjuk, hogy a világról szóló igaz tudásunk mennyiben köszönhető a két operandus által kifejezhető igaz tudásnak. Kicsit másként: ha csak a diszjunkció igazságát ismerjük, nem tudhatjuk, hogy ez A vagy B, esetleg mindkettő egyifejű igazságának köszönhető-e. A diszjunkció a hétköznapi kommunikáció során leggyakrabban használt műveletek közé tartozik.$\concept{TAUTOLOGY}\equiv \top \defi A \lor \lnot A$
tautológia (hun) – mindig igaz (hun) – tautology (eng)
A tautológia az a művelet, amely úgy kapcsol össze két állítást, hogy azok együttese mindig igaz legyen. Ebben a minőségében a kontradikció ellentéte. Ha azt mondjuk, Esik az eső, vagy nem esik az eső., akkor ez mindképpen igaz. Persze, kérdés, hogy mi az értelme vagy inkább mi a haszna az ilyen műveletnek. A példamondat alapján nem igazán érezni, pedig igenis nagy jelentősége van a tautológiáknak: a logikai következtetési szabályaink nagy részét ezek adják. A művelet nulláris, konstans.★
A tizenhat bináris művelet áttekintése után érdemes őket egy táblázatban egyszerre felsorolni (az ellentéteikkel és igazságtáblázataikkal együtt).| művelet | jele | formula | 11 | 10 | 01 | 00 | ellentéte | |||||||
| ellentmondás | $\bot$ | $A \land \lnot A$ | 0 | 0 | 0 | 0 | tautológia | |||||||
| konnegáció | $\not\lor, \downarrow, \nabla, \mid\mid$ | $\lnot A \land \lnot B$ | 0 | 0 | 0 | 1 | diszjunkció | |||||||
| retroszubtrakció | $\nleftarrow$ | $\lnot A \land B$ | 0 | 0 | 1 | 0 | retrokondicionális | |||||||
| kontraprojekció | $\not\triangleleft$ | $\lnot A $ | 0 | 0 | 1 | 1 | projekció | |||||||
| szubtrakció | $\nrightarrow$ | $A \land \lnot B$ | 0 | 1 | 0 | 0 | kondicionális | |||||||
| kontra-retroprojekció | $\not\triangleright$ | $\lnot B$ | 0 | 1 | 0 | 1 | retroprojekció | |||||||
| biszubtrakció | $\nleftrightarrow, \oplus, \veebar$ | $(A \land \lnot B) \lor (\lnot A \land B)$ | 0 | 1 | 1 | 0 | bikondicionális | |||||||
| exklúzió | $\not\land, \uparrow, \mid, \mid\mid$ | $\lnot A \lor \lnot B$ | 0 | 1 | 1 | 1 | konjunkció | |||||||
| konjunkció | $\land$, & | $A \land B$ | 1 | 0 | 0 | 0 | exklúzió | |||||||
| bikondicionális | $\leftrightarrow, \Leftrightarrow, \equiv$ | $ (\lnot A \lor B) \land (A \lor \lnot B)$ | 1 | 0 | 0 | 1 | biszubtrakció | |||||||
| retroprojekció | $\triangleright$ | $B$ | 1 | 0 | 1 | 0 | kontra-retroprojekció | |||||||
| kondicionális | $\rightarrow, \supset, \Rightarrow$ | $\lnot A \lor B$ | 1 | 0 | 1 | 1 | szubtrakció | |||||||
| projekció | $\triangleleft$ | $A$ | 1 | 1 | 0 | 0 | kontraprojekció | |||||||
| retrokondicionális | $\leftarrow, \subset, \Leftarrow$ | $A \lor \lnot B$ | 1 | 1 | 0 | 1 | retroszubtrakció | |||||||
| diszjunkció | $\lor$, v | $A \lor B$ | 1 | 1 | 1 | 0 | konnegáció | |||||||
| tautológia | $\top, \models$ | $A \lor \lnot A$ | 1 | 1 | 1 | 1 | ellentmondás | |||||||
Kijelentéskalkulus
A kijelentéslogika a propozíciók és a köztük levő logikai műveletek, logikai kapcsolók struktúrájával foglalkozik. E struktúra alapját a kijelentéskalkulus (Propositional Calculus, PC) adja. A propozícionális kalkulus axiómakészletének definiálásához nyilván kevesebb elemre van szükség, ezért a PC nyelve szűkebb a kijelentéslogika nyelvénél. A PC logikája a következő nyelvi alapelemekre építhető fel.$\mathscr{L}_{PC}(A,B,C, \lnot, \to)$
| $A,B,C$ | formula (propozíció) |
| $\lnot$ | tagadás logikai művelet |
| $\to$ | kondicionális logikai művelet |
$A \to (B \to A)$
$(A \to B) \to ((A \to (B \to C)) \to(A \to C))$
$(\lnot A \to \lnot B) \to (B \to A)$
$\concept{LOGICAL\_CONSEQUENCE\_RELATION}\equiv\Rightarrow\veebar\Leftarrow\veebar\Leftrightarrow$
logikai következmény relációk (hun) – logical consequence relations (eng)
A három szimbólumot értelemszerűen az egyik, a másik vagy a mindkét irányból vett következmény fennállásának jelzésére használjuk. A logikai következmény reláció nem az adott nyelvhez tartozik, a nyelvhez képest metanyelvi relációnak kell tartanunk. A (PC) következtetési szabálya a modus ponens (MP), ami ami szűkebb értelemben véve nem tartozik a kalkulushoz, de ettől még nélkülözhetetlen.$\concept{(MP)} \defi \{A, (A \to B)\} \Rightarrow B$
modus ponens következtetési szabály (hun) – modus ponens inference rule (eng)
A modus ponens úgy értelmezhetjük, hogy ha egy A kijelentés és a belőle vont bármely B utótagú (A$\to$B) implikáció része igaz az adott nyelven, akkor a kondicionális B utótagja is igaz. Vannak más következtetési szabályok is, de ezek mind levezethetők a sémaaxiómák és a modus ponens szabály formulái alapján. Ezekre támaszkodva az összes ismert összefüggést, következtetési sémát le lehet vezetni. [♦] Csak a szemléltetés kedvéért álljon itt pár további következtetési szabály.$A \lor B \defi \lnot(\lnot A \land \lnot B)$
diszjunkció definiálása (hun) – definition of conjuction (eng)
$A \land B \Rightarrow A$
$A \land B \Rightarrow B$
konjunkció eliminálása (hun) – elimination of conjuction (eng)
$A \Rightarrow A \lor B$
$B \Rightarrow A \lor B$
diszjunkció bevezetése (hun) – introduction of disjunction (eng)
$\{\lnot B, (A \to b)\} \Rightarrow \lnot A $
modus tollens következtetési szabály (hun) – modus tollens inference rule (eng)
kettős tagadás törvénye (hun) – double negation law (eng)
$(A \to B) \Rightarrow (\lnot B \to \lnot A)$
kondicionális kontrapozíció törvénye (hun) – law of conditional contraposition (eng)
$(A \leftrightarrow B) \Rightarrow (A \to B)$
$(A \leftrightarrow B) \Rightarrow (B \to A)$
bikondicionális eliminálása (hun) – elimination of biconditional (eng)
$A \leftarrow B \defi B \rightarrow A$
retrokondicionális definiálása (hun) – kondicionális konverzió (hun) – implikációs konverzió (hun) – definition of retroconditional (hun) – conditinal conversion (eng)
Megállapíthatunk még egy további fontos szabályszerűséget: a nulladrendű kijelentéslogika zárt a logikai operátorokra, ami azt jelenti, hogy minden művelet eredménye propozíció, vagyis a műveletekkel képzett új állítások a logika érvényességi körén belül maradnak. Logikai szempontból még tovább lehetne egyszerűsíteni a kijelentéslogika nyelvét, ha ki akarnánk használni azt a tényt, hogy mind az exklúzió ($\mid$), mind a konnegáció ($\mid\mid$) azzal az egyedi tulajdonsággal rendelkezik, hogy segítségével az összes többi logikai művelet kifejezhető. A tagadás – például – az exklúzió segítségével a következőképpen írható fel.$\lnot A \Leftrightarrow A \mid A$
Ez azt jelenti, hogy a propozicionális logika minden művelete átalakítható lenne, és minden formulája felírható lenne e két logikai operátor valamelyikével. A következő táblában bemutatom, hogy az exklúzióra támaszkodva hogyan lehet reprezentálni a tizenhat logikai kapcsoló műveletét.
| művelet | formula ($\mid$) | |||||||||||||
| ellentmondás | $(A \mid (A \mid A))\mid(A \mid (A \mid A))$ | |||||||||||||
| konnegáció | $((A \mid A)\mid(B \mid B))\mid((A \mid A)\mid(B \mid B))$ | |||||||||||||
| retroszubtrakció | $((A \mid B)\mid B)\mid((A \mid B)\mid B)$ | |||||||||||||
| kontraprojekció | $A \mid A$ | |||||||||||||
| szubtrakció | $(A\mid(A\mid B))\mid(A\mid(A\mid B))$ | |||||||||||||
| kontra-retroprojekció | $B \mid B$ | |||||||||||||
| biszubtrakció | $((A\mid(A\mid B)) \mid( (B\mid(A \mid B)))$ | |||||||||||||
| exklúzió | $A \mid B$ | |||||||||||||
| konjunkció | $(A \mid B)\mid(A \mid B)$ | |||||||||||||
| bikondicionális | $((A\mid(A\mid B)) \mid ((A \mid B)\mid B))\mid((A\mid(A\mid B)) \mid ((A \mid B)\mid B))$ | |||||||||||||
| retroprojekció | $B$ | |||||||||||||
| kondicionális | $A\mid(A\mid B)$ | |||||||||||||
| projekció | $A$ | |||||||||||||
| retrokondicionális | $(A \mid B)\mid B$ | |||||||||||||
| diszjunkció | $(A \mid A)\mid(B \mid B)$ | |||||||||||||
| tautológia | $(A \mid A)\mid((A\mid A) \mid (A \mid A))$ | |||||||||||||
Predikátumlogika
A nulladrendű logika a kijelentések, a mondatok szintjén keresi a szabályszerűségeket. A mondat, az állítás ilyenkor bonthatatlan egészet alkot, nem tudjuk, nem tudhatjuk, mi van a propozíciók belsejében. Csak az számít, hogy igaz vagy hamis-e az állítás. Ezen a szinten a logika csak "tudomásul veszi", de érdemben nem boncolgatja a logikai igazság/hamisság kérdését. Az állításlogikában ezért a logikai elemzés fókusza a mondatok közti műveletek vizsgálatára irányul. A logikai apparátus leíróerejét azáltal lehet növelni, ha a logikai elemzés hatókörét kiterjesztjük úgy, hogy a kijelentések "belsejét" is vizsgálni tudjuk. Ehhez az kell, hogy "felbontsuk" a mondatot, megengedjük a kijelentések összetevőkre bontását és azok vizsgálatát. Amikor ezt tesszük, akkor lépünk át az elsőrendű vagy predikátumlogika világába. Ennek leírásához használhatjuk a következő predikátumlogikai nyelvet.$\mathscr{L}_{QL}(\mathscr{L}_{PL}, m,n,o, t,s,r, \forall, \exists, =)$
| $m,n,o$ | változó |
| $t,s,r$ | konstans |
| $\forall$ | univerzális kvantor |
| $\exists$ | egzisztenciális kvantor |
| $=$ | egyenlőség |
$\concept{CONSTANT} \equiv t \;|\; s \;|\; r $
konstans (hun) – név (hun) – constant (eng) – name (eng)
$\concept{PREDICATE}\equiv A\;|\;B \;|\; C \;|\; P \;|\; R$
predikátum (hun) – logikai függvény (hun) – funktor (hun) – reláció (hun) – függvény (hun) – predicate (eng) – logical function (eng) – relation (eng) – function (eng) – functor (eng)
Az elsőrendű logika segítségével mondhatunk olyan mondatokat, amelyekben valamely reláció konkrét előfordulására vonatkozóan teszünk egy állítást úgy, mint a következő példában (tekintsünk most el attól, hogy a 'szürke' minősítést pontosan hogyan is kell érteni, kezelni logikailag):Ráró szürke. (= A Ráró nevű ló szürke.)
Az ilyen mondatok azonban kevéssé érdekesek a logika számára. Ha csak konstansok és relációk lennének ebben a formális nyelvben, akkor ezt a logikát kevéssé lehetne használni, mert így gyenge általánosítóerővel rendelkezne. Azzal léphetünk nagyot az általánosíthatóság, az absztrakció irányában, ha az individuumokat jelző konstansok (konkrét nevek) helyett változókat alkalmazunk. Általánosíthatjuk a mondatainkat, ha a relációkba változókat írunk:Az x ló szürke. (= ló(x) szürke)
Ekkor viszont nem tudjuk egyértelműen, mire (itt: melyik lóra) vonatkozik az állítás. Az ilyen kijelentés nem tartalmas, nem egyértelmű. Azt mondjuk rá, hogy nyitott mondat. Az az izgalmas a logika számára, ha olyan általános kijelentéseket fogalmazhat meg, amelyek tartalmasak, zártak. Ilyen mondatok képzésére valók a kvantorok, amelyekkel "le lehet zárni" és ezzel egyértelművé lehet tenni a nyitott logikai mondatokat. Két kvantort használunk. Az egyik az univerzális kvantor (jelentése: 'minden x-re igaz, hogy', jele: $\forall$), a másik az egzisztenciális kvantor (jelentése: 'van olyan x, amire igaz, hogy', jele: $\exists$). A kvantorokkal "leköthetjük" a szabad változókat, ami azt is jelenti egyben, hogy általános (és tartalmas, zárt) állításokat nyerhetünk az alkalmazásukkal. Ha azt mondjuk, hogy:'minden ló szürke' – $\forall m$ ló(x) szürke 'létezik ló, ami szürke' – $\exists x$ ló(x) szürke
akkor olyan állításokhoz jutunk, amelyek már logikailag értékelhetőek (és az első kijelentést hamisnak minősíthetjük, hiszen vannak nem szürke lovak is, a másodikat állítást viszont igaznak tarthatjuk, hiszen láttunk szürke lovat). Az elsőrendű logika nyelvét ki kell egészítenünk a fent bemutatott új kategóriákkal. Szükség van (i) a változó fogalmára, ami a logikai kifejezésekben valamely halmaz elemeit mint lehetséges értékhordozókat helyettesítő nyelvi jel, illetve szükség van két – a kategóriák terjedelmét jelentő előfordulásokra vonatkozó – új operátorrra is. Az egyik (ii) az egzisztenciális kvantor, amely legalább egy előfordulás létezését tételezi a logikai kifejezésben, a másik (iii) az univerzális kvantor, amely az összes előfordulás létezését fejezi ki a logikai kifejezésben.$\concept{VARIABLE}\equiv m\;|\; n \;|\; o \;|\; p $
változó (hun) – variable (eng)
$\concept{EXISTENTIAL\_QUANTIFIER} \equiv \exists $
egisztenciális kvantor (hun) – existential quantifier (eng)
$\concept{UNIVERSAL\_QUANTIFIER} \equiv \forall$
univerzális kvantor (hun) – universal quantifier (eng)
A két kvantor közül elég csak az egyiket felvenni a nyelvbe alapkategóriaként, a másik már definálható a segítségével. A predikátumkalkulusban így is teszünk majd. A következő fejezetben mutatom meg, hogyan.Predikátumkalkulus
Természetesen a predikátumlogikának is van kalkulusa, a predikátumkalkulus (Predicate Calculus – QC). A QC-kalkulust sem elemzem itt alaposabban, elégnek tartom bemutatni az axiómsémáit. A predikátumkalkulus a predikátumlogika nyelvének azon legszűkebb része, amelyre támaszkodva minden predikátumlogikai formulát ki lehet fejezni valahogyan. A predikátumkalkulusnak egyszerűbb nyelv is elégséges, amit a következőféleképpen lehet definiálni.$\mathscr{L}_{QC}(A,B,C, m,n,o, t, \forall, \lnot, \to, =)$
| $A,B,C$ | formula |
| $m,n,o$ | változó |
| $t,s,r$ | konstans |
| $\forall$ | univerzális kvantor |
| $\lnot$ | tagadás logikai művelet |
| $\to$ | kondicionális logikai művelet |
| $=$ | egyenlőség |
$A \to (B \to A)$
$(A \to(B \to C)) \to ((A \to B) \to (A \to C))$
$(\lnot A \to \lnot B) \to (B \to A)$
$\forall o (A \to A^{t/o})$
$\forall o(A \to B) \to (\forall o(A) \to \forall o(B)))$
$A \to \forall o(A)$
$o=o$
$(m=n) \to (A^{m/o} \to A^{n/o})$
$\concept{EXISTENTIAL\_QUANTIFIER}(m)\equiv\exists m \defi\lnot\forall\lnot m$
egzisztenciális kvantor(hun) – existential quantifier (eng)
A (QC) levezetési szabálya a (MP) modus ponens, de természetesen minden más állításlogikai következtetési szabályt alkalmazhatunk. A későbbiekben szükségünk lehet arra, hogy amikor az egzisztenciális kvantort alkalmazzuk, akkor mondhassuk azt, hogy abból az individuumból, aminek a létezését állítjuk az egzisztenciális kvantor segítségével, abból csak egyetlen egy van. Ezt a következő formulával fejezhetjük ki.$\concept{UNIQUENESS\_QUANTIFIER}(m)\equiv\exists! \equiv\exists! m\equiv\exists! m(\rel{P}(m)) \defi\exists m\forall n(\rel{P}(n)\leftrightarrow m=n)$
unicitás kvantor (hun) – uniqueness quantifier (eng) – unique existential quantifier (eng)
A módosított kvantort (operátort) úgy kell értelmezni, hogy 'létezik egy és csak egy', és mindig mellé kell képzelni egy predikátumot, amire vonatkoztatjuk a kvantort (aminek az egyeleműségét állítjuk). Mivel az operátor segítségével az egyelemű predikátumokat tudjuk kifejezni, és a fenti formulát szokás unicitássémának is nevezni [Ruzsa] ezért használhatjuk az unicitás kvantor (vagy unicitás operátor) megnevezést.Relációelmélet
A formális nyelvek által definiált fogalmak valamilyen struktúrát alkotnak, a struktúrák vázát pedig mindig az adott nyelvbe felvett relációk adják. Bármilyen relációs struktúrát építünk is fel, minden esetben szükség van arra, hogy a relációkat magukat is jellemezni tudjuk. A relációelmélet ezt a feladatot végzi el. Három fogalom van az elmélet központjában: a reláció, a függvény és a művelet. Ezek mindegyikét különféle tulajdonságokkal jellemezhetjük, műveletek értelmezhetünk közöttük, és mindegyik levezethető a másikból, tehát bármelyiket megtehetnénk egy formális elmélet alapfogalmául. Én azt a megközelítést fogadom el, amely szerint a reláció fogalmából kell kiindulni, és ebből lehet levezetni előbb a függvény, majd a művelet fogalmát.Relációelméleti alapfogalmak
A relációelméleti fogalmak rövid bemutatását a relációhoz kapcsolódó fogalomcsokor tárgyalásával kezdem. Első lépésként sorba veszem a relációt leíró tulajdonság- és műveletfogalmakat. Ezután módszertanilag annak kéne következnie, hogy bemutassam a reláció fogalmára építhető kalkulust, de ezt addig nem lehet megtenni, amíg be nem vezettük a művelet fogalmát. Ezért a relációs tulajdonságfogalmak bemutatása után rátérek a függvény és a művelet fogalmainak tárgyalására, és csak miután ezekkel végeztem, azután vázolom fel röviden a relációelmélet kalkulusát, a relációalgebrát. A reláció fogalmával kettő vagy több dolog közti kapcsolatot ragadhatjuk meg. Ez azt jelenti, hogy mindig meg kell tudnunk adni, hogy milyen dolgok közötti viszonyt írunk le az adott reláció segítségével. Ehhez meg kell adnunk egy (vagy több) halmazt, amely(ek)nek elemeit összekapcsolhatjuk egymással a reláció keretében. Az összekapcsolt elemeket relátumoknak nevezzük. Az összekapcsolt elemeket adjuk meg a reláció argumentumában, és attól függően, hogy hány elemet kapcsolunk össze beszélhetünk a reláció argumentumszámáról. A relációk jellemzéséhez kiindulhatunk az alábbi nyelvből.$\mathscr{L}_{RL}$($ \mathscr{L}_{QL}, \rel{R}, \rel{F}, \rel{O}, \langle m,n,o\rangle, \mathbb{X}\times\mathbb{X}, \mathbb{Dom}, \mathbb{Im})$
| $\langle m,n,o\rangle$ | rendezett n-s |
| $\rel{R},\rel{P},\rel{Q}$ | reláció |
| $\rel{F}$ | függvény |
| $\rel{O}$ | művelet |
| $\mathbb{X}\times \mathbb{X}$ | Descartes szorzat |
| $\mathbb{Dom}$ | értelmezési tartomány |
| $\mathbb{Im}$ | képtartomány |
$\concept{RELATION}(m,n)\equiv\langle m,n\rangle \equiv (m,n)\in \rel{R}\subset\mathbb{X}\times\mathbb{X}\equiv \rel{R}(m,n)\defi \{\{m\},\{m,n\}\}$
reláció (hun) – relation (eng)
A relációkhoz (függvényekhez) kapcsolódik két fontos osztályfogalom, az értelmezési tartomány és értékkészlet. Ezeket a következő módon emelhetjük be a modellünkbe.$\concept{DOMAIN}\equiv\mathbb{Dom}(\rel{R}(m,n))\equiv\mathbb{Dom}(\rel{R})\equiv\mathbb{Dom}\equiv\mathbb{D}\defi \{m: \exists n(\rel{R}(m,n))\}$
értelmezési tartomány (hun) – domain (eng)
$\concept{IMAGE}\equiv\mathbb{Im}(\rel{R}(m,n))\equiv\mathbb{Im}(\rel{R})\equiv\mathbb{Im}\equiv\mathbb{I}\defi \{n: \exists m(\rel{R}(m,n))\}$
képtartomány (hun) – kép (hun) – értékkészlet (hun) – image (eng) – range (eng) – co-domain (eng)
A relációk egyik legáltalánosabb tipizálási lehetőségét az adja, ha arra figyeljük, hogy a reláció által összekapcsolt dolgok homogének-e vagy sem, azaz ugyanabból a halmazból vesszük-e őket vagy sem. Ha igen, akkor homogén (homogeneous), ha nem, akkor heterogén (heterogeneous) relációról beszélünk. Még mindig a legáltalánosabb szinten maradva definiálhatunk négy nevezetes relációt, amelyekre később még szükségünk lesz.$\concept{UNIVERSAL\_RELATION}(m,n)\equiv\underline{\rel{U}}(m,n)\equiv\underline{\rel{U}}\equiv\underline{\rel{F}}(m,n)\equiv\underline{\rel{F}}\defi\forall m\forall n(\rel{R}(m,n))$
teljes reláció (hun) – univerzális reláció (hun) – universal relation (eng) – full relation (eng)
$\concept{IDENTITY\_RELATION}(m,n)\equiv\underline{\rel{I}}(m,n)\equiv\underline{\rel{I}}\defi\forall m \forall n (\rel{R}(m,n) \leftrightarrow m=n)$
azonosság (reláció) (hun) – egység reláció (hun) – diagonál(is) reláció (hun) – egyenlőség(i reláció) (hun) – identitás (reláció) (hun) – identity (relation) (eng) – diagonal (relation) (eng)
$\concept{EMPTY\_RELATION}(m,n)\equiv\underline{\rel{E}}(m,n)\equiv\underline{\rel{E}}\defi\forall m\forall n(\lnot \rel{R}(m,n))$
üres reláció (hun) – null reláció (hun) – empty relation (eng) – null relation (eng)
$\concept{DIVERSITY\_RELATION}(m,n)\equiv\underline{\rel{D}}(m,n)\equiv\underline{\rel{D}}\defi\forall m \forall n (\rel{R}(m,n) \leftrightarrow m \ne n)$
különbözőség (reláció) (hun) – egyenlőtlenség(i reláció) (hun) – antidiagonális (reláció) (hun) – differencia (reláció) (hun) – inkompatibilitás(i reláció) (hun) – diverzitás(i reláció) (hun) – difference (eng) – incompatibility (relation) (eng) – antidiagonal (relation) (eng) – diversity (relation) (eng)
Mivel a fenti négy relációtípus fontos szerepet tölt be a relációelméletben, ezért saját nevet kapott, nem pedig a rá jellemző tulajdonság alapján lehet hivatkozni rájuk. A következő blokkban azokat a relációtulajdonságokat mutatom be, amelyek önmagukban "csak" tulajdonságok, de a relációfogalomhoz kapcsolva őket egy sor nevezetes, gyakran használt relációt azonosíthatunk velük. A különböző korok, diszciplinák, megközelítések, emberek ugyanarra a problémára sokszor nagyon hasonló, de bizonyos pontokon így vagy úgy eltérő tulajdonságokat tartottak fontosnak bevezetni, ezért az egymáshoz közeli fogalmakat csoportokba rendezve mutatom be. A reflexivitással kapcsolatos tulajdonságok azt a minőséget próbálják megragadni, hogy az elemek között tételezett reláció vonatkoztatható-e az elemekre önmagukra is, vagyis összeköthetők-e az elemek önmagukkal vagy sem. Ezt fejezi ki a reflexivitás tulajdonsága. Hétköznapi példa lehetne a reflexivitásra a szereti reláció, hiszen valaki szerethet másokat, de szeretheti magát is, ám ez példa kevés lehet a reflexivitás fennállásához, hiszen nem minden esetben érvényesül. Vannak ugyanis olyan emberek, akik nem szeretik önmagukat. Márpedig a reflexivitás minőségét csak akkor érdemes egy relációhoz kötni, ha az minden elemre vonatkoztatható. Ebben az értelemben elfogadható példa lehet az egyidős reláció, hiszen egy ember egyidős lehet valaki mással, de mindig egyidős önmagával. Olyan eset is előfordulhat, amikor a reflexivitás sosem érvényesül. Például a szülője vagy a testvére relációra hivatkozhatunk, amikoris mondhatjuk, hogy senki sem lehet önmaga szülője vagy testvére.$\concept{REFLEXIVE}(\rel{R}(m,n))\defi\forall m(\rel{R}(m,m))$
reflexív (hun) – reflexive (eng) – erősen reflexív (hun) – strongly reflexive (eng)
$\concept{IRREFLEXIVE}(\rel{R}(m,n))\defi\forall m(\lnot \rel{R}(m,m))$
irreflexív (hun) – antireflexív (hun) – irreflexive (eng) – antireflexive (eng)
$\concept{NON-REFLEXIVE}(\rel{R}(m,n))\defi\exists m(\lnot \rel{R}(m,m))$
nem-reflexív (hun) – non-reflexive (eng)
$\concept{SECONDARILY\_REFLEXIVE}(\rel{R}(m,n))\defi\forall m\forall n(\rel{R}(m,n) \to \rel{R}(n,n))$
másodlagosan reflexív (hun) – szekunder reflexív (hun) – secondarily reflexive (eng) – shift reflexive (eng)
$\concept{INVERSE\_SECONDARILY\_REFLEXIVE}(\rel{R}(m,n))\defi\forall m\forall n(\rel{R}(m,n) \to \rel{R}(m,m))$
fordítottan másodlagosan reflexív (hun) – feltételesen reflexív (hun) – conditional reflexive (eng) – inverse secondarily reflexive (eng)
$\concept{COREFLEXIVE}(\rel{R}(m,n))\defi\forall m\forall n(\rel{R}(m,n) \to m=n)$
koreflexív (hun) – üres (hun) – vacuous (eng) – coreflexive (eng)
A relációtulajdonságok másik csoportjába tartoznak a szimmetricitással kapcsolatos tulajdonságok. Ekkor arra kérdezünk rá, hogy ha a reláció két elem között fennáll, akkor vajon fennáll-e a fordított irányban is, vagy másként: ha a reláció igaz, akkor igaz-e a konverze. Szimmetrikus a testvére reláció, hiszen ha A testvére B-nek, akkor ez fordítva is igaz, vagyis B testvére A-nak. Léteznek azonban olyan relációk is, amelyekre minden esetben kizárhatjuk a szimmetricitást. Ilyen például az idősebb reláció: ha A idősebb B-nél, akkor B nem lehet sosem idősebb A-nál.$\concept{SYMMETRIC}(\rel{R}(m,n))\defi\forall m\forall n(\rel{R}(m,n) \to \rel{R}(n,m))$
szimmetrikus (hun) – symmetric (eng)
$\concept{ASYMMETRIC}(\rel{R}(m,n))\defi\forall m\forall n(\rel{R}(m,n) \to \lnot \rel{R}(n,m))$
aszimmetrikus (hun) – antiszimmetrikus (hun) – szigorúan antiszimmetrikus (hun) – asymmetric (eng) – antisymmetric (eng)
$\concept{ANTISYMMETRIC}(\rel{R}(m,n))\defi\forall m\forall n((\rel{R}(m,n) \land \rel{R}(n,m)) \to m=n)$
antiszimmetrikus (hun) – identitív (hun) – antisymmetric (eng) – identitive (eng)
$\concept{NON-SYMMETRIC}(\rel{R}(m,n))\defi\rel{R}(m,n) \land \lnot \rel{R}(n,m))$
nem-szimmetrikus (hun) – non-symmetric (eng)
Fontos csoportot képeznek azok a tulajdonságok, amelyek a teljességgel, összehasonlíthatósággal, összekapcsoltsággal, egyértelműséggel kapcsolatosak. Mindig jó tudnunk egy relációval kapcsolatban, hogy a reláció tartóhalmazának minden elemére kiterjed-e a reláció érvénye vagy sem. Különösen fontos kérdés ez az összehasonlíthatóság miatt. A ismeri relációt például nem tarthatjuk teljesnek, mert egy csoporton belül nem mindenki ismerheti egymást, ezért a csoport tagjai között nem állíthatunk fel egy teljes ismertségi hálót. Az egyértelműség kérdése pedig azért lehet fontos, mert sokszor akarhatjuk azt, hogy egy reláció fennállásához egyértelmű következményeket rendelhessünk. Ennek "kiderítésére" is érdemes tulajdonságokat definiálni.$\concept{WEAKLY\_CONNECTED}(\rel{R}(m,n))\defi\forall m \forall n \forall o (\rel{R}(m,n) \land \rel{R}(m,o) \to (n = o \lor \rel{R}(n,o) \lor \rel{R}(o,n)))$
gyengén összefüggő (hun) – weakly connected (eng) – weakly connex (eng) – összehasonlítható (hun) – comparable (eng)
$\concept{CONNECTED}(\rel{R}(m,n))\defi\forall m\forall n(m\ne n\to (\rel{R}(m,n) \lor \rel{R}(n,m)))$
összefüggő (hun) – konnex (hun) – connex (eng) – connected (eng) – lineáris (hun) – teljes (hun) – complete (eng) – totális (hun) – total (eng) – összehasonlítható (hun) – comparable (eng)
$\concept{STRONGLY\_CONNECTED}(\rel{R}(m,n))\defi\forall m\forall n(\rel{R}(m,n) \lor \rel{R}(n,m))$
erősen összefüggő (hun) – strongly connex (eng) – strongly connected (eng) – totally connected (eng) – totálisan összefüggő (hun) – teljes (hun) – complete (eng) – totális (hun) – total (eng) – összehasonlítható (hun) – comparable (eng)
$\concept{DICHOTOME}(\rel{R}(m,n))\defi\forall m\forall n(m\ne n\to (\rel{R}(m,n) \land \lnot \rel{R}(n,m)) \lor (\lnot \rel{R}(m,n) \land \rel{R}(n,m)))$
dichotóm (hun) – összehasonlítható (hun) – comparable (eng) – totális (hun) – teljes (hun) – total (eng) – dichotomous (eng) – complete (eng)
$\concept{TRICHOTOME}(\rel{R}(m,n))\defi\forall m\forall n((\rel{R}(m,n) \land \lnot \rel{R}(n,m) \land m\ne n) \lor (\lnot \rel{R}(m,n) \land \rel{R}(n,m) \land m\ne n) \lor m=n)$
trichotóm (hun) – lineáris (hun) – trichotomous (eng)
$\concept{COMPARABLE}(\rel{R}(m,n))\defi\forall m\forall n \forall o (\rel{R}(m,n) \to (\rel{R}(m,o) \lor \rel{R}(o,n)))$
összehasonlítható (hun) – comparable (eng)
$\concept{INDIFFERENT}(\rel{R}(m,n))\defi \forall m \forall n(\rel{R}(m,n)\land \rel{R}(n,m))$
indifferens (hun) – erősen indifferens (hun) – erősen közömbös (hun) – strongly indifferent (eng) – indifferent (eng) – egyenlő értékű (hun) – equal in value (eng) – ugyanolyan, mint (hun) – same as (eng)
$\concept{INCOMPARABLE}(\rel{R}(m,n))\defi \forall m \forall n(\lnot\rel{R}(m,n)\land \lnot\rel{R}(n,m))$
összehasonlíthatatlan (hun) – gyengén közömbös (hun) – gyengén indifferens (hun) – incomparable (eng) – weakly indifferent (eng) – ugyanolyan értékes, mint (hun) – same value as (eng)
$\concept{LEFT-TOTAL}(\rel{R}(m,n))\defi\forall m\exists n(\rel{R}(m,n))$
balról totális (hun) – totális (hun) – sorozatos (hun) – szeriális (hun) – serial (eng) – sorozat (hun) – left-total (eng) – extendable (eng)
$\concept{RIGHT-TOTAL}(\rel{R}(m,n))\defi\forall n\exists m(\rel{R}(m\rel{R}(m,n))$
jobbról totális (hun) – right-total (eng)
$\concept{LEFT-UNIQUE}(\rel{R}(m,n))\defi\forall m \forall n \forall o ((\rel{R}(m,o) \land \rel{R}(n,o)) \to m=n)$
balról egyértelmű (hun) – inverz-funkcionális (hun) – inverse functional (eng)
$\concept{RIGHT-UNIQUE}(\rel{R}(m,n))\defi\forall m \forall n \forall o ((\rel{R}(m,n) \land \rel{R}(m,o)) \to n=o)$
jobbról egyértelmű (hun) – funkcionális (hun) – parciális függvény (hun) – partial function (eng) – functional relation (eng) – right-unique (eng) – univalent (eng)
$\concept{DENSE}(\rel{R}(m,n)) \defi \forall m\forall o(\rel{R}(m,o) \to \exists n(\rel{R}(m,n) \land \rel{R}(n,o)))$
sűrű (hun) – dense (eng) – gyengén sűrű (hun) – weakly dense (eng)
$\concept{CONVERGENT}(\rel{R}(m,n)) \defi \forall m\forall n\forall o\exists p((\rel{R}(o,m) \land \rel{R}(o,n)) \to ( \rel{R}(m,p) \land \rel{R}(n,p)))$
konvergens (hun) – convergent (eng)
A későbbiekben talán a legtöbbet azzal a tulajdonságcsoporttal foglalkozunk majd, amely a tranzitivitással, ciklikussággal, aciklikussággal kapcsolatos. A relációk segítségével való következtetéseinket támogathatja az, ha tudjuk, hogy ha az adott reláció fennáll bizonyos elemek között, akkor ebből következtethetünk arra tényre, hogy minden más elem közt is érvényes. Példaként hivatkozhatunk a idősebb relációra: ha A idősebb B-nél, és B idősebb C-nél, akkor már – mivel ez a reláció tranzitív – következtethetünk arra, hogy A idősebb C-nél. A későbbiekben a tranzitivitás tulajdonsága a preferencia fogalmával kapcsolatban fog gyakran előkerülni. Nem könnyíti meg a fogalom értelmezését az a tény, hogy fontossága miatt sokféle módon próbálták meg kifejezni a tranzitivitás minőségét, így sok versengő, egymásra hasonlító definíció született e téren.$\concept{TRANSITIVE}(\rel{R}(m,n))\defi\forall m \forall n \forall o ((\rel{R}(m,n) \land \rel{R}(n,o)) \to \rel{R}(m,o))$
tranzitív (hun) – transitive relation (eng)
$\concept{INTRANSITIVE}(\rel{R}(m,n))\defi\forall m \forall n \forall o ((\rel{R}(m,n) \land \rel{R}(n,o)) \to \lnot \rel{R}(m,o))$
intranzitív (hun) – atranzitív (hun) – antitranzitív (hun) – intransitive (eng) – atransitive (eng) – antitransitive (eng)
$\concept{QUASI-TRANSITIVE}(\rel{R}(m,n))\defi\forall m \forall n \forall o ((\rel{R}(m,n) \land \rel{R}(n,o) \land m \ne o) \to \rel{R}(m,o))$
kvázitranzitív (hun) – quasi-transitive (eng)
$\concept{ALIO-TRANSITIVE}(\rel{R}(m,n))\defi\forall m \forall n \forall o ((\rel{R}(m,n) \land \rel{R}(n,o)) \to (\rel{R}(m,o) \lor m=o))$
aliotranzitív (hun) – alio-transitive (eng)
$\concept{SEMI-TRANSITIVE}(\rel{R}(m,n))\defi\forall m \forall n \forall o \forall p ((\rel{R}(m,n) \land \rel{R}(n,o)) \to (\rel{R}(m,p) \lor \rel{R}(p,o)))$
szemitranzitív (hun) – semi-transitive (eng)
$\concept{FERRERS\_PROPERTY}(\rel{R}(m,n))\defi\forall m \forall n \forall o \forall p ((\rel{R}(m,n) \land \rel{R}(o,p)) \to \\(\rel{R}(m,p) \lor \rel{R}(o,n)))$
Ferrers tulajdonság (hun) – Ferrers property (eng)
$\concept{NEGATIVELY\_TRANSITIVE}(\rel{R}(m,n))\defi\forall m \forall n \forall o ((\rel{R}(m,n) \to (\rel{R}(m,o)) \lor \rel{R}(o,n)))$
negatívan tranzitív (hun) – negatively transitive relation (eng)
$\concept{NON-TRANSITIVE}(\rel{R}(m,n))\defi\exists x \exists n \exists z((\rel{R}(m,n) \land \rel{R}(n,o)) \land \lnot \rel{R}(m,o))$
nem-tranzitív (hun) – atranzitív (hun) – intranzitív (hun) – non-transitive (eng) – intransitive (eng) – atransitive (eng)
$\concept{CIRCULAR}(\rel{R}(m,n))\defi\forall m \forall n \forall o ((\rel{R}(m,n) \land \rel{R}(n,o)) \to \rel{R}(o,m))$
cirkuláris (hun) – circular (eng)
$\concept{ACIRCULAR}(\rel{R}(m,n))\defi\forall m \forall n \forall o ((\rel{R}(m,n) \land \rel{R}(n,o)) \to \lnot \rel{R}(o,m))$
acirkuláris (hun) – acircular (eng)
$\concept{EUCLIDEAN}(\rel{R}(m,n))\defi\forall m \forall n \forall o ((\rel{R}(m,n) \land \rel{R}(m,o)) \to \rel{R}(n,o))$
euklideszi (hun) – euclidean (eng)
$\concept{ANEUCLIDEAN}(\rel{R}(m,n))\defi\forall m \forall n \forall o ((\rel{R}(m,n) \land \rel{R}(m,o)) \to ( \lnot \rel{R}(n,o) \land \lnot \rel{R}(o,n)))$
aneuklideszi (hun) – antieuclidean (eng) – aneuclidean (eng) – ineuclidean (eng) – antitransitive (eng)
$\concept{CATENARY}(\rel{R}(m,n))\defi\forall m \forall n \exists o (\rel{R}(m,n) \to ((\rel{R}(n,o) \lor \rel{R}(o,m)))$
katenáris (hun) – láncolt reláció (hun) – nem bipoláris (hun) – catenary (eng) – non-bipolar (eng)
$\concept{ACATENARY}(\rel{R}(m,n))\defi\forall m \forall n \forall o (\rel{R}(m,n) \to ( \lnot \rel{R}(n,o) \land \lnot \rel{R}(o,m)))$
akatenáris (hun) – nem-láncolt (hun) – bipoláris (hun) – non-catenary (eng) – acatenary (eng) – bipolar (eng)
$\concept{CONFLUENT}(\rel{R}(m,n))\defi\forall m \forall n \forall o \exists p((\rel{R}(m,n) \land \rel{R}(m,o)) \to (\rel{R}(n,p) \land \rel{R}(o,p)))$
konfluens (hun) – confluent (eng) – directed (eng) – incesztuális reláció (hun) – incestual relation (eng)
$\concept{ACONFLUENT}(\rel{R}(m,n))\defi\forall m \forall n \forall o \exists p(\rel{R}(m,n) \land \rel{R}(m,o)) \to \lnot (\rel{R}(n,p) \land \rel{R}(o,p)))$
akonfluens (hun) – aconfluent (eng)
Ahhoz, hogy további fontos relációtulajdonságokat tudjunk definiálni, szükség van arra, hogy bevezessünk olyan új fogalmakat, amelyek elkülönítik a reláció valamely részét adott tulajdonság mentén, és csak az így lehatárolt részre vonatkoznak.$\concept{SYMMETRIC\_PART\_OF\_}\rel{R}(m,n)\equiv \rel{I(R)}\defi\{(m,n)\in \mathbb{X}\times\mathbb{X} | (m,n)\in \rel{R}\land (n,m)\in \rel{R}\}$
$\rel{R}$ szimmetrikus része (hun) – symmetric part of $\rel{R}$ (eng) – $\rel{R}$ szimmetrikus faktora (hun) – symmetric factor of $\rel{R}$ (eng)
$\concept{ASYMMETRIC\_PART\_OF\_}\rel{R}(m,n)\equiv \rel{P(R)}\defi\{(m,n)\in \mathbb{X}\times\mathbb{X} | (m,n)\in \rel{R}\land (n,m)\notin \rel{R}\}$
$\rel{R}$ aszimmetrikus része (hun) – asymmetric part of $\rel{R}$ (eng) – $\rel{R}$ aszimmetrikus faktora (hun) – asymmetric factor of $\rel{R}$ (eng)
A későbbiekben még definiálni fogunk további származtatott relációkat (☜) A fenti relációrész-fogalmak segítségével bevezethetünk itt olyan tulajdonságokat, amelyekre támaszkodnunk majd a későbbiekben a racionalitás problémájának tárgyalásakor. Adottnak veszünk egy relációt, és annak egy részére írunk elő követelményeket.$\concept{TRIPLE\_ACYCLIC}(\rel{R}(m,n))\defi\forall m\forall n\forall o((m,n)\in \rel{P(R)}\land (n,o)\in \rel{P(R)}\to (o,m)\notin \rel{P(R)})$
hármas aciklusos (hun) – triple acyclic relation (eng)
$\concept{ACYCLIC}(\rel{R}(m,n))\defi\forall t \in \mathbb{N}^+, \forall m^1, m^ 2, \dots, m^t \in \mathbb{X}(\forall \tau \in \{1,2, \dots, t- 1\}(m^t,m^{t+ 1})\\\in \rel{P(R)})\to (m^t,m^1)\notin \rel{P(R)}$
aciklusos (hun) – acyclic relation (eng)
$\concept{CONSISTENT}(\rel{R}(m,n))\defi\forall t \in \mathbb{N}^+, \forall m^1, m^ 2, \dots, m^t \in \mathbb{X}((m^1,m^2)\in \rel{P(R)}\land\forall \tau\in\{2,3,\dots,t - 1\}\\((m^\tau,m^{\tau + 1})\in\rel{R}))\to (m^t,m^1)\in \rel{R}$
(Suzumura) konzisztens (hun) – (Suzumura) consistent relation (eng)
A konzisztencia fogalmára később bemutatok másfajta definíciókat is (☜) Mivel a tranzitivitás tulajdonsága sok cselekvéselméleti fogalomhoz kapcsolódik, a gazdasági cselekvések területén pedig a legfontosabb fogalmak közé tartozik, a tranzitivitás tulajdonságára támaszkodva további fogalmakat határozhatunk meg. Ha van egy $\rel{R}(m,n)$ tranzitív relációnk, akkor definiálhatjuk a következő tulajdonságokat [Amart]$\concept{PP-TRANSITIVE}(\rel{R}(m,n))\defi \forall m \forall n \forall o(((\rel{R}(m,n)\land \lnot\rel{R}(n,m)) \land (\rel{R}(n,o) \land \lnot\rel{R}(o,n))) \to \\(\rel{R}(m,o) \land \lnot \rel{R}(o,m)))$
PP-tranzitív (hun) – PP-transitive (eng) – kvázitranzitív (hun) – quasi-transitive (eng)
$\concept{IP-TRANSITIVE}(\rel{R}(m,n))\defi \forall m \forall n \forall o(((\rel{R}(m,n)\land \rel{R}(n,m))\land (\rel{R}(n,o) \land \lnot\rel{R}(o,n)))\to \\(\rel{R}(m,o)\land \lnot\rel{R}(m,o))$
IP-tranzitív (hun) – IP-transitive (eng)
$\concept{PI-TRANSITIVE}(\rel{R}(m,n))\defi \forall m \forall n \forall o(((\rel{R}(m,n) \land \lnot\rel{R}(n,m)) \land (\rel{R}(n,o)\land \rel{R}(o,n)))\to \\\rel{R}(m,o) \land \lnot\rel{R}(o,m)))$
PI-tranzitív (hun) – PI-transitive (eng)
$\concept{II-TRANSITIVE}(\rel{R}(m,n))\defi \forall m \forall n \forall o(((\rel{R}(m,n)\land \rel{R}(n,m)) \land (\rel{R}(n,o) \land \rel{R}(o,n))) \to \\(\rel{R}(m,o) \land \rel{R}(o,m)))$
II-tranzitív (hun) – II-transitive (eng)
Az így definiált tulajdonságok között fontos összefüggések állapíthatók meg, de ezeket nem mutatom be formális módon, csak megemlítek párat közülük [Amart] [SvenO] Igaz például az, hogy ha egy reláció tranzitív (jelöljük ezt itt T-vel), akkor fennáll mind a négy belőle levezethető PP-, II-, IP- és PI-tranzititás tulajdonság is, de fontos tézis az is, miszerint a PP- és PI-, illetve a PP- és II-tulajdonságok együttes fennállásából következik a T tranzitivitás létezése. Ezeket a kapcsolatokat szemléltethetjük egy ábra segítségével.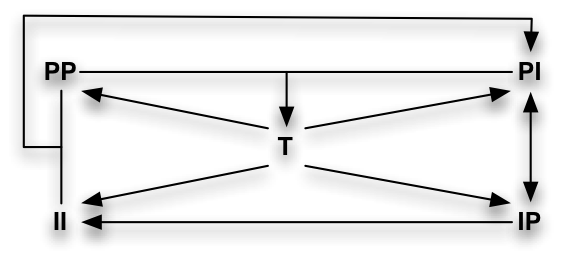
A preferencia fogalmának tárgyalásakor még visszatérünk ezekre az összefüggésekre, és ott további relációk megnevezésével egyszerűsítünk az itt bevezetett tranzitivitási tulajdonságok formuláin (☜) Akkor lehet majd rámutatni arra, hogy honnan származnak a most definiált tulajdonságok megnevezései. Az eddig definiált relációtulajdonságok között természetesen nem teljesen függetlenek egymástól, rengeteg összefüggés van közöttük. Itt csak azokat mutatom be, amelyekre a későbbiekben szükség lesz [Kotar] [♦]
$\concept{ASYMMETRIC}\to \concept{IRREFLEXIVE}$
$\concept{STRONGLY\_CONNECTED}\to \concept{IRREFLEXIVE}$
$\concept{TRANSITIVE}\to \concept{CONSISTENT}$
$\concept{TRANSITIVE}\to \concept{QUASY\_TRANSITIVE}$
$\concept{CONSISTENT}\to \concept{ACYCLIC}$
$\concept{QUASY\_TRANSITIVE}\to \concept{ACYCLIC}$
$\concept{ACYCLIC}\to \concept{TRIPLE\_ACYCLIC}$
Nevezetes relációk
A legelemibb rendezésfogalmakat a különféle relációtulajdonságok segítségével lehet elkülöníteni egymástól. Sajnos, a rendezési fogalmak világában sincs terminológiai tisztaság, gyakran találkozhatunk mind a homonimitás, mind a szinonimitás jelenségével. Ebben a könyven leginkább a rendezési relációkat fogom használni, de fontosnak tartom megemlíteni itt a többi nevezetes relációt is.$\concept{TOLERANCE} \defi\concept{REFLEXIVE} \land \concept{SYMMETRIC}$
tolerancia reláció (hun) – kompatibilitási reláció (hun) – hasonlósági reláció (hun) – compatibility relation (eng) – similarity relation (eng) – tolerance relation (eng)
$\concept{PARTIAL\_EQUIVALENCE}\defi\concept{TRANSITIVE} \land \concept{SYMMETRIC}$
részleges ekvivalencia reláció (hun) – partial equivalence relation (eng) – per (eng)
$\concept{EQUIVALENCE}\defi\concept{REFLEXIVE} \land \concept{SYMMETRIC} \land \concept{TRANSITIVE}$
ekvivalenciareláció (hun) – ekvivalencia (hun) – equivalence (eng)
$\concept{PARTIAL\_ORDER}\defi\concept{REFLEXIVE} \land \concept{ANTISYMMETRIC} \land \concept{TRANSITIVE}$
részben rendezés (hun) – parciális rendezés (hun) – részleges rendezés (hun) – gyenge rendezés (hun) – gyenge részben rendezés (hun) – nem szigorú rendezés (hun) – weak order (eng) – weak partial order (eng) – partial order (eng)
$\concept{WEAK\_ORDER}\defi\concept{COMPLETE} \land \concept{TRANSITIVE}$
gyenge rendezés (hun) – weak order (eng)
$\concept{LINEAR\_ORDER}\defi\concept{COMPLETE} \land \concept{ANTISYMMETRIC} \land \concept{TRANSITIVE}$
lineáris rendezés (hun) – linear order (eng)
$\concept{STRICT\_ORDER}\defi\concept{IRREFLEXIVE} \land \concept{TRANSITIVE}$
szigorú rendezés (hun) – szigorú rendezési reláció (hun) – erős részben rendezés (hun) – irreflexív rendezés (hun) – strict order (eng) – strict weak order (eng) – strong order (eng) – strong weak order (eng)
$\concept{LINEAR\_PARTIAL\_ORDER}\defi\concept{REFLEXIVE} \land \concept{ANTISYMMETRIC} \land \concept{TRANSITIVE} \land \concept{DICHOTOMOUS}$
nem szigorú elrendezés reláció (hun) – teljes parciális rendezés (hun) – lineáris parciális rendezés (hun) – totális parciális rendezés (hun) – total partial order (eng) – linear partial order (eng)
$\concept{LINEAR\_STRICT\_ORDER}\defi\concept{IRREFLEXIVE} \land \concept{TRANSITIVE} \land \concept{DICHOTOMOUS}$
szigorú elrendezés (hun) – teljes szigorú rendezés (hun) – lineáris szigorú rendezés (hun) – totális szigorú rendezés (hun) – total strict order (eng) – linear strict order (eng) – total strong order (eng) – linear strong order (eng)
$\concept{PREORDER}\defi\concept{REFLEXIVE} \land \concept{TRANSITIVE}$
előrendezés (hun) – kvázirendezés (hun) – preorder (eng) – quasi order (eng)
$\concept{WEAK\_ORDER}\defi\concept{REFLEXIVE} \land \concept{TRANSITIVE} \land \concept{DICHOTOMOUS}$
gyenge rendezés (hun) – lineáris előrendezés (hun) – weak order (eng) – linear preorder (eng) – total preorder (eng)
$\concept{WEAK\_PARTIAL\_ORDER}\defi\concept{ANTISYMMETRIC} \land \concept{TRANSITIVE}$
gyenge részben rendezés (hun) – partial order (eng) – weak partial order (eng)
$\concept{LINEAR\_WEAK\_PARTIAL\_ORDER}\defi\concept{ANTISYMMETRIC} \land \concept{TRANSITIVE} \land \concept{DICHOTOMOUS}$
részben elrendezés (hun) – teljes gyenge részben rendezés (hun) – total weak partial order (eng) – linear weak partial order (eng)
$\concept{TOURNAMENT} \defi \concept{TRANSITIVE} \land \concept{DICHOTOMOUS}$
turnament (hun) – tournament (eng)
A relációról szóló könyvében a rendezési fogalmakról Jurij A. Srejder készített egy érdekes áttekintő ábrát (jelölve a relációk egymáshoz való viszonyát is) [Srejd] amit korábban további relációkkal egészítettem ki [Szaka] Érdemesnek tartom ezt az ábrát itt is bemutatni.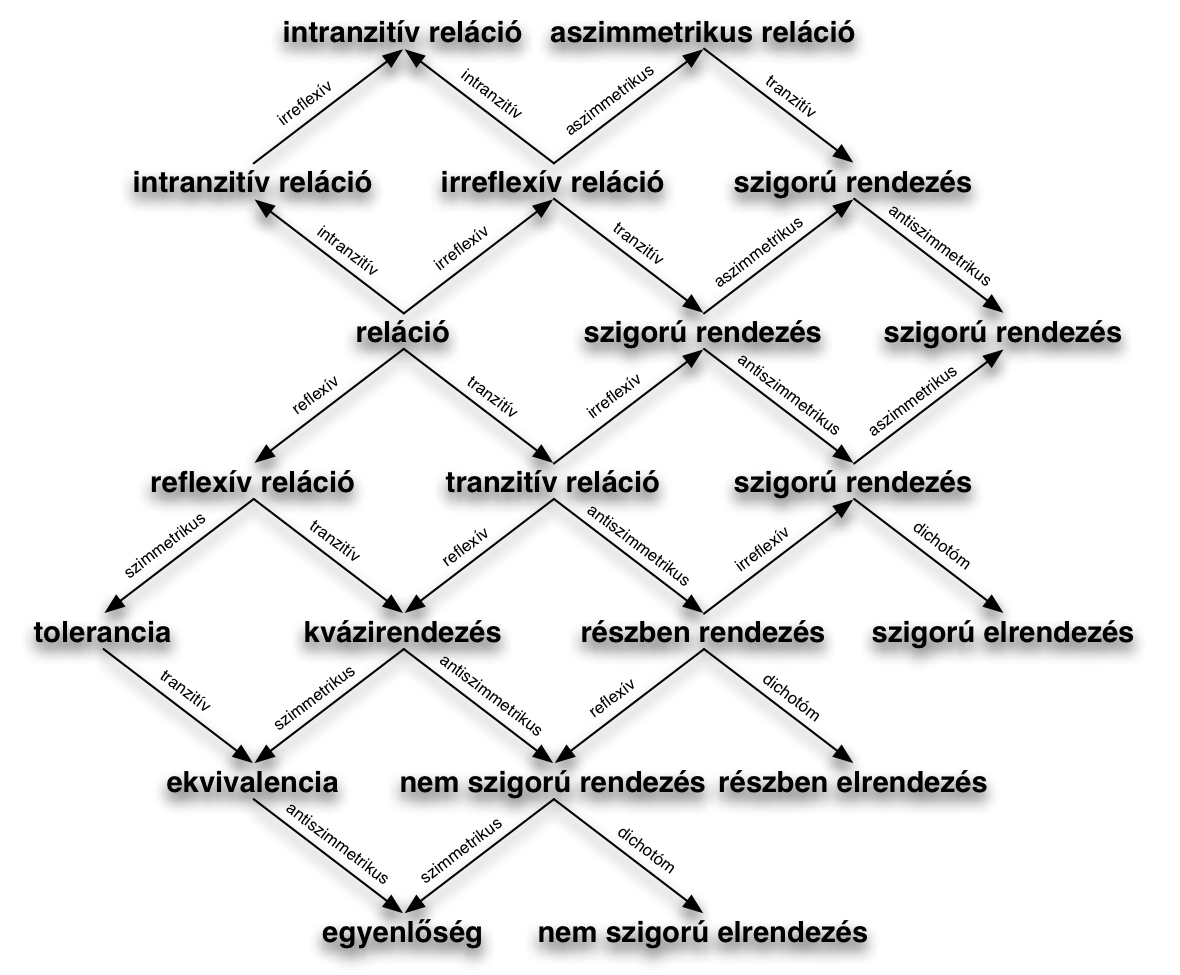
A relációkat mindig a hozzájuk tartozó (tartó)halmazon defináljuk. Ha veszünk egy halmazt és definiálunk rajta egy vagy több relációt, akkor már reláció struktúráról beszélhetünk. A struktúra fogalmának tehát nagyon egyszerű (mert nagyon általános) meghatározása van: egy halmazból és egy (vagy több) reláció együttese.
$\concept{STRUCTURE}\equiv \mathfrak{S}\equiv \mathfrak{F}\equiv \mathfrak{T} \defi (\mathbb{T},\{\rel{R}_i\}_{i\in\mathbb{N}^{+}})$
struktúra (eng) – structure (eng) – relációs struktúra (eng) – relation structure (eng) – modell (hun) – model (eng) – algebra (hun) – algebra (eng)
Az eddig tárgyalt rendezési fogalmak is felfoghatók valamilyen struktúrának, de persze nemcsak rendezési fogalmak léteznek. Definiálhatunk egy nagyon fontos relációs struktúrát (ami még mindig rendezési fogalom). A neve fa vagy fastruktúra [Patri] de nevezhetjük hierarchiának is [Szaka] Ezt a struktúrát mind a tudományban, mind a hétköznapi életben rengeteget használjuk, a szervezési, szerveződési technikák egyik legfontosabb típusa. A fa(struktúra) definícióját a következőképpen adhatjuk meg.$\concept{TREE}(m,n)\defi$ $ \;\;\forall n \exists! r \exists! m (\rel{R}^{\ast}(r,n)$ $\land (m\ne r \to \rel{R}(m,n))$ $\land \lnot \rel{R}^{+}(n,n))$
fa (hun) – tree (eng) – monohierarchia (hun) – mono-hierarchy (eng)
Az első részformula azt határozza meg, hogy a fának egy és csak egy csúcspontja (root) van, a formula második összetevője pedig azt definálja, hogy a csúcselemen kívül minden más elemhez egy és csak egy közvetlenül megelőző elem (predecessor) tartozik. [♦] (☜) A harmadik formula az aciklikusságot mondja ki a reláció $\rel{R}^{+}$ tranzitív lezártja (☜) segítségével – más formában, mint az aciklikusságra adott korábbi definíció (☜) Be kell itt vezetnem két olyan további rendezésfogalmat, amelyekre a későbbiekben még hivatkozni szeretnék. Ha van két részben rendezett halmazunk (A és B), a két halmazon értelmezett $A\times B$ Descartes-szorzatán kétféle rendezést definiálhatunk: a sorrendezést és a lexikografikus rendezést. Ezeket a következőképpen határozhatjuk meg.$\concept{ARCHIMEDEAN\_ORDER}((a_1,b_1),(a_2,b_2))\equiv(a_1,b_1) \le (a_2,b_2) \defi a_1 \le^{\ast} a_2 \land b_1\le^{'} b_2$
sorrendezés (hun) – product order (eng) – arkhimédeszi rendezés (hun) – archimedean order (eng)
$\concept{LEXICOGRAPHIC\_ORDER}((a_1,b_1),(a_2,b_2))\equiv(a_1,b_1) \le (a_2,b_2) \defi a_1 <^{\ast} a_2 \lor (a_1 = a_2 \land b_1 \le^{'} b_2)$
lexikografikus rendezés (hun) – alfabetikus rendezés (hun) – ábécé szerinti rendezés (hun) – lexicographic order (eng) – dictionary order (eng)
Mindkét rendezés nagyon fontos. A sorrendezés példaként hivatkozhatunk arra, ahogyan sorba rakjuk a természetes számokat, míg a lexikografikus rendezés legismertebb példája a természetes nyelv szavainak szótári (ábécé szerinti) rendezése.Függvény
A reláció egyik típusának fogható fel a függvény fogalma, de – ahogy azt már említettem – a függvényt is lehetne alapkategóriának tekinteni és le lehetne vezetni belőle a reláció fogalmát. A reláció kategóriatanát azzal folytatom, hogy előbb veszem a függvény mint speciális reláció fogalmát, majd bemutatom, hogy milyen fontosabb függvénytulajdonságok vannak.$\concept{FUNCTION}(m,n)\equiv\rel{F}(m,n)\equiv\rel{F}(m)=n\equiv\rel{F}\equiv\rel{F}:\mathbb{Dom}\mapsto \mathbb{Cod}\defi\concept{LEFT-TOTAL}(\rel{F}) \land $ $\concept{RIGHT-UNIQUE}(\rel{F})$
függvény (hun) – leképezés (hun) – function (eng)
$\concept{INVERSE\_FUNCTION}(m,n)\equiv\rel{F}^{- 1}(m,n)\defi\concept{RIGHT-TOTAL}(\rel{F}) \land \concept{LEFT-UNIQUE}(\rel{F})$
inverz függvény (hun) – inverz leképezés (hun) – inverse function (eng)
$\concept{BIUNIQUE}(\rel{F}(m,n))\defi \concept{LEFT-UNIQUE}(\rel{F}) \land \concept{RIGHT-UNIQUE}(\rel{F})$
egy-egyértelmű (hun) – egyértelmű (hun) – biunique (eng) – unique (eng)
$\concept{BITOTAL}(\rel{F}(m,n))\defi\concept{LEFT-TOTAL}(\rel{F}) \land \concept{RIGHT-TOTAL}(\rel{F})$
bitotális (hun) – 1:1-es reláció (hun) – bitotal (eng) – bitotal relation (eng) – 1-1 relation (eng)
$\concept{INJECTIVE}(\rel{F}(m,n))\defi\concept{FUNCTION}(\rel{F}) \land \concept{LEFT-UNIQUE}(\rel{F})$
injektív (hun) – egyrétű (hun) – injective (eng)
$\concept{SURJECTIVE}(\rel{F}(m,n))\defi\concept{FUNCTION}(\rel{F}) \land \concept{RIGHT-TOTAL}(\rel{F})$
szürjektív (hun) – ráképzés (hun) – szuperjektív (hun) – lefedő (hun) – surjective (eng)
$\concept{BIJECTIVE}(\rel{F}(m,n))\defi\concept{INJECTIVE}(\rel{F}) \land \concept{SURJECTIVE}(\rel{F})$
bijektív (hun) – egyrétűen lefedő (hun) – bijective (eng)
$\concept{SERIES}(\rel{F}(m,n))\defi\concept{FUNCTION}(\rel{F}) \land \mathbb{D}=\mathbb{N}$
sorozat (hun) – series (eng)
Ha speciális relációstruktúraként értelmezünk olyan struktúrát, amelyben ugyanazon a halmazon értelmezünk egy rendezési relációt és egy függvényt, akkor további fontos tulajdonságokat definiálhatunk. Többször lehet fontos az a kérdés, vajon egy rendezés által kialakított sorrend megőrződik-e akkor, ha definiálunk egy függvényt ugyanazon a halmazon. Ezt írhatjuk le a monotonicitás körébe tartozó tulajdonságokkal.$\concept{MONOTONE}(\rel{F}(m,n))\defi \forall m \forall n(m\le n \to \rel{F}(m)\preceq \rel{F}(n))$
monoton (hun) – monoton növekvő (hun) – monotone (eng) – monotonic (eng) – monotonically increasing (eng) – isotone (eng) – order-preserving (eng)
$\concept{ANTITONE}(\rel{F}(m,n))\defi \forall m \forall n(m\le n \to \rel{F}(n)\preceq \rel{F}(m))$
antiton (hun) – komonoton (hun) – monoton csökkenő (hun) – co-monotone (eng) – monotonically decreasing (eng) – antitone (eng) – anti-monotone (eng) – order-reserving (eng)
Művelet
A műveletek (operációk) speciális függvényként értelmezhetők, de természetesen fordítva is igaz, és definiálható lenne a függvény a művelet fogalmára támaszkodva. A műveletre gyakran használják még az operáció kifejezést is, ez magyarázza azt a tényt, hogy a műveletek argumentumaira, változóira operandusként hivatkozunk. A műveletek esetében szinte kizárólagos az ún. infix reprezentációs mód, amikor a művelettel összekapcsolt változókat (operandusokat) a műveleti jel két oldalára írjuk. A következő blokkban bemutatom a művelet és a legfontosabb művelettulajdonságok definícióit.$\concept{OPERATION}(m,n)\equiv \rel{O}(m,n)\equiv m\rel{O}n\defi\concept{FUNCTION}(m,n) \land \mathbb{Dom}=\mathbb{Cod}$
művelet (hun) – operáció (hun) – belső összekapcsolás (hun) – operation (eng)
$\concept{ASSOCIATIVE}(\rel{O}(m,n))\defi\forall m \forall n \forall o (m \rel{O} (n \rel{O} o)=(m \rel{O} n) \rel{O} o)$
asszociatív (hun) – társítható (hun) – csoportosítható (hun) – associative (eng)
$\concept{COMMUTATIVE}(\rel{O}(m,n))\defi\forall m \forall n (m \rel{O} n=n \rel{O} m)$
kommutatív (hun) – felcserélhető (hun) – commutative (eng)
$\concept{DISTRIBUTIVE}(\rel{O}(m,n)|\rel{Q})\defi\forall m \forall n \forall o ((m \rel{O} (n \rel{Q} o)=(m \rel{O} n) \rel{Q} (m \rel{O} o))$
$\rel{O}$ disztributív $\rel{Q}$-ra (hun)) – szétosztható (hun) – széttagolható (hun) – distributive (eng)
$\concept{DISTRIBUTIVE}(\rel{Q}(m,n)|\rel{O})\defi\forall m \forall n \forall o ((n \rel{Q} o) \rel{O} m=(n \rel{O} m) \rel{Q} (o \rel{O} m))$
$\rel{Q}$ disztributív $\rel{O}$-ra (hun) – szétosztható (hun) – széttagolható (hun) – distributive (eng)
$\concept{IDEMPOTENT}(\rel{O}(m,n))\defi\forall m (m \rel{O} m=m)$
idempotens (hun) – önhatványozó (hun) – azonos hatványú (hun) – idempotent (eng)
$\concept{ABSORPTIVE}(\rel{O}(m,n)|\rel{Q})\defi\forall m \forall n (m \rel{Q} (m \rel{O} n)=m)$
$\rel{O}$ abszorbtív $\rel{Q}$-ra (hun) – elnyelő (hun) – adjunktív (hun) – absorptive (eng)
$\concept{ABSORPTIVE}(\rel{Q}(m,n)|\rel{O})\defi\forall m \forall n (n \rel{O} (m \rel{Q} n)=m)$
$\rel{Q}$ abszorbtív $\rel{O}$-ra (hun) – elnyelő (hun) – adjunktív (hun) – absorptive (eng)
Relációműveletek
Miután már ismerjük a műveletek tulajdonságait, típusait, visszatérhetünk annak a kérdésnek a tisztázásához, hogy milyen műveletek definiálhatók a relációk között. A relációműveletek azért fontosak, mert ha relációkat kapcsolunk össze relációkkal (műveletek mint speciális relációk segítségével), akkor valamilyen halmazon (a relációk halmazán) értelmezett reláció(k)ról, művelet(ek)ről van szó, vagyis ilyen módon is valamilyen struktúrát állítunk elő. A műveletek között unáris és bináris műveletet definiálunk.$\concept{R-CONVERSION}\equiv\rel{R}^{- 1}(m,n)\equiv \rel{R}^{- c}(m,n)\equiv\rel{R}^{- 1}\equiv\rel{R}^{- c}\defi\forall n \forall n (\rel{R}^{- 1}(m,n) \leftrightarrow \rel{R}(n,m))$
relációkonvertálás (hun) – konverzképzés (hun) – inverzképzés (hun) – megfordítás (hun) – relation conversion operation (eng) – relation converse operation (eng) – relation inverse operation (eng)
Ha van egy $\rel{R}(m,n)$ relációnk, akkor annak a konverze (vagyis a konverzreláció) úgy állítható elő, hogy a relációba kapcsolt elemek, a relátumok sorrendjét felcseréljük egymással. A relációkonvertálást a köznyelvben sokszor új terminus bevezetésével oldjuk meg. Például a gyereke(Béla,Pál) reláció konverze a gyereke$^{- 1}$(Béla,Pál), de nem ezt alkalmazzuk, hanem inkább egy új kifejezést alkotunk és a szülője(Pál,Béla) relációt használjuk. A definícióból adódik, hogy ha a konverziót kétszer egymás után alkalmazzuk, akkor az eredeti relációhoz jutunk vissza. A konverzreláció a megfordított reláció, a konverzió maga a megfordítási művelet. A konverzió műveletét mind a mondatszerű, mind a szószerű megnyilatkozások szintjén értelmezhetjük. Amikor az összekapcsolt mondatok belső struktúráját vizsgáljuk, akkor kondicionális konverzióról beszélünk (☜) amikor a mondatokon belüli összetevők szerkezetét, akkor kategoriális konverzióról (☜) Az első esetben a művelet értelmezési tartománya a propozíciókból, a második esetben a kategoriális propozíciók alkotórészeiből, predikátumokból, kategóriákból áll. [♦] Timothy Williamson egy tanulmányában kifejtette, hogy a konverzreláció nem tekinthető önálló relációnak, sőt, voltaképpen teljesen megegyezik az alaprelációval [Timot] vagyis nem tekinthető másnak, mint a szokásostól eltérő, alternatív jelölési konvenciónak. Ahogy a formális nyelvekben ugyanazt a relációt is többféleképpen jelölhetjük (például $\rel{R}mn$, $m\rel{R}n$ vagy $\rel{R}(m,n)$), úgy mutatunk ugyanarra a tartalomra az alapreláció $\rel{R}(m,n)$, illetve a konverzreláció $\rel{R}(n,m)$ vagy $\rel{R}^{- 1}(m,n)$ jeleivel, csak éppen más sorrendben rögzítjük a relátumokat – ami csak megállapodás kérdése, semmi más. Ebben az értelemben a konverzrelációt jelző terminusok mind szinonímái az alapreláció terminusainak, tehát a gyereke relációnak szinonímája a szülője reláció, mivel tartalmilag teljesen ugyanazt jelentik. Ez természetesen csak logikai szempontból igaz. A hétköznapi nyelvhasználatban ezt az összefüggést nem is érzékeljük, nem is érvényesítjük. Sok helyen, sokan szinonimaként használják az inverz és konverz terminusokat, és vannak, akik megkülönböztetik őket egymástól. Én is így különbséget teszek köztük, de kiderül majd az is, hogy vannak helyzetek, amikor valóban megegyezik a két művelet eredménye (tehát bizonyos feltételek esetén valóban kezelhetjük őket szinonimaként).$\concept{R-INVERSION}\equiv\rel{R}^{- i}(m,n)\equiv\rel{R}^{- i}\defi\forall m \forall n(\rel{R}^{- i}(m,n) \leftrightarrow \rel{R}(\neg m,\neg n))$
relációinvertálás (hun) – inverzképzés (hun) – relation inverse operation (eng)
Ha van egy $\rel{R}(m,n)$ relációnk, akkor annak az inverze úgy állítható elő, hogy a relációba kapcsolt elemek, a relátumok komlementereit (tagadásait) kapcsoljuk össze. A definíció alapján könnyű belátni, hogy két egymás utáni inverzió visszaadja magát az eredeti relációt. Transzformációs művelet még az obverzió (átalakítás) is, de ezt csak később tudom bemutatni és definiálni (☜) mivel tágyalásához szükség van még további fogalmak ismeretére. Itt elemzem viszont az általános kontrapozíció műveletét, hogy aztán a későbbi fejezetekben kitérjek majd a további típusaira is.$\concept{R-CONTRAPOSITION}\equiv\rel{R}^{- p}(m,n)\equiv\rel{R}^{- p}\defi\forall m \forall n(\rel{R}^{- p}(m,n) \leftrightarrow \rel{R}(\neg n,\neg m))$
kontrapozíció (hun) – transzpozíció (hun) – contraposition (eng) – transposition (eng)
Ha van egy $\rel{R}(m,n)$ relációnk, akkor annak a kontrapozíciója (vagyis a reláció kontraponáltja) úgy állítható elő, hogy a relációba kapcsolt elemek, a relátumok komplementereit fordított sorrendben kapcsoljuk össze. A kontrapozíciót is értelmezhetjük mind a mondatszerű, mind a szószerű megnyilatkozások szintjén. Összekapcsolt mondatok szerkezetének átalakításakor kondicionális kontrapozícióról (☜) mondatokon belüli összetevők átstrukturálásakor kategoriális kontrapozícióról (☜) beszélünk. A kontrapozíció definíciójából az is látszik, hogy a kontrapozíció nem más, mint a konverzió inverze, illetve az inverzió konverze. [♦]$\concept{R-CONTRAPOSITION}\leftrightarrow \concept{R-CONVERSION}(\concept{R-INVERSION})\leftrightarrow \concept{R-INVERSION}(\concept{R-CONVERSION})$
Két további fontos unáris relációműveletet a reláció halmazelméleti kötődése alapján határozhatunk meg. Ha a relációt speciális halmazként fogjuk fel, akkor alkalmazható rá a halmazokon értelmezett komplementálás művelete, ami az univerzális halmazra vonatkoztatva a reláció tagadásaként is felfogható.$\concept{R-COMPLEMENTATION}\equiv\rel{R}^{- t}(m,n)\equiv\rel{R}^{- t}\equiv\overline{\rel{R}}(m,n))\equiv\overline{\rel{R}}\defi\forall m\forall n (\overline{\rel{R}}(m,n) \leftrightarrow \lnot \rel{R}(m,n)$
relációkomplementálás (hun) – relation complementation (eng) – relation transzpozíció (hun) – relation transposition (eng)
Ha pedig egymás után alkalmazzuk a reláció konvertálásának és komplementálásának (tagadásának) műveletét, akkor a reláció duális párjához jutunk. [♦]$\concept{R-DUAL}\equiv\rel{R}^{- d}(m,n))\equiv\rel{R}^{- d}\defi\forall m\forall n (\rel{R}^{- d}(m,n) \leftrightarrow \lnot \rel{R}(n,m)\equiv\overline{\rel{R}^{- c}}(m,n)$
duálreláció (hun) – duális (reláció) (hun) – dual relation (eng)
A relációk között bináris műveleteket is értelmezhetünk. A két halmazelméleti művelet (az únió- és metszetképzés), valamint a két aritmetikai művelet (a szorzás és összeadás) mintájára bevezethetjük a következőket.
$\concept{R-INTERSECTION}\equiv\times(\rel{R}(m,n),\rel{Q}(m,n))\equiv \times(\rel{R},\rel{Q})\equiv \rel{R}\times\rel{Q}\defi\forall m\forall n (\rel{R} \times \rel{Q}(m,n) \leftrightarrow (\rel{R}(m,n) \land $
$\rel{Q}(m,n))$
relációmetszés (hun) – relation intersection (eng)
$\concept{R-UNION}\equiv+(\rel{R}(m,n),\rel{Q}(m,n))\equiv +(\rel{R},\rel{Q})\equiv \rel{R}+\rel{Q}\defi\forall m \forall n (\rel{R}+ \rel{Q}(m,n) \leftrightarrow (\rel{R}(m,n) \lor \rel{Q}(m,n))$
relációegyesítés (hun) – relációúnió (hun) – relációegyesítés (hun) – relation union (eng)
$\concept{R-COMPOSITION}\equiv\divideontimes(\rel{R}(m,n),\rel{Q}(m,n))\equiv\divideontimes(\rel{R},\rel{Q})\equiv\rel{R}\divideontimes\rel{Q}\defi\forall m \forall n (\rel{R} \divideontimes \rel{Q}(m,n)) \leftrightarrow (\rel{R}(m,o) \land $
$\rel{Q}(o,n))$
relációszorzás (hun) – relatív szorzat (hun) – kompozíció (hun) – multiplikáció (hun) – szuperpozíció (hun) – relációkompozíció (hun) – relation product (eng) – relative multiplication (eng) – relative product (eng) – superposition (eng) – composition (eng)
$\concept{R-ADDITION}\equiv\dagger(\rel{R}(m,n),\rel{Q}(m,n))\equiv\dagger(\rel{R},\rel{Q})\equiv\rel{R}\dagger\rel{Q}\defi\forall m\forall n (\rel{R} \dagger \rel{Q}(m,n)) \leftrightarrow (\rel{R}(m,o)\\ \lor \rel{Q}(o,n))$
relációösszeadás (hun) – összeadás (hun) – relatív összeadás (hun) – relative addition (eng) – relative sum (eng)
Bár a fenti bináris relációműveletek mindegyike szerepet kap a relációalgebra struktúrájában, közülük is "kiemelkedik" a relációszorzat vagy másik gyakori nevén a relációkompozíció művelete. A mindennapi fogalmi készletünkben is előfordulnak olyan fogalmak, amelyek ezt a műveletet használják. Egyszerű példát lehet hozni erre a rokonsági fogalmak köréből. Vegyük a gyereke relációt, amivel összeköthetjük Pétert és Katalint (gyereke(Péter,Katalin)). Ezután vegyük a testvére relációt, amivel összekapcsolhatjuk Máriát és Pétert (testvére(Mária,Péter)). A két relációt összekomponálva a következő eredményt kapjuk: A relációműveletek segítsévégel további származtatott relációkat definiálhatunk, amelyek fontosak lesznek a későbbiekben. Az itt definiált tranzitív lezártja reláció voltaképp ugyanúgy relációművelet, mint a fentiek, csak épp itt végtelen sorozat segítségével tudjuk a pontos meghatározást megadni.$\concept{TRANSITIVE\_CLOSURE}(\rel{R})\equiv \rel{R}^{+} \defi (\rel{R}^1=\rel{R} \land (i >1 \to \rel{R}^{i+ 1}=\rel{R}\divideontimes\rel{R}^i))\to\bigcup \limits_{i\in\mathbb{N}^{+}}\rel{R}^i$
tranzitív lezártja (hun) – transitive closure (eng)
$\concept{REFLEXIVE\_TRANSITIVE\_CLOSURE}(\rel{R}) \equiv \rel{R}^{\ast}\defi a$
reflexív tranzitív lezártja (hun) – reflexive transitive closure (eng)
Ha egy reláció megegyezik a tranzitív lezártjával, akkor a reláció egyben tranzitív, de a legtöbbször nem ez a helyzet, és a reláció, illetve a tranzitív lezártja különbözik egymástól. A reláció tranzitív lezártja fogalom segítségével a korábbinál jóval egyszerűbben is definiálhatjuk a – racionalitás leírásában fontossá váló – konzisztencia fogalmát (☜) Ehhez a reláció tranzitívját, illetve aszimmetrikus részét kell összekapcsolni egymással [Bosse]$\concept{CONCISTENT\_RELATION}\defi \forall m \forall n(\rel{R}^{+}(m,n) \to \lnot\rel{P(R)}(n,m))$
konzisztens reláció (hun) – consistent relation (eng)
A formula egyszerűen értelmezhető: egy reláció konzisztens, ha tetszőleges két elemet, m-t és n-t a reláció tranzitív lezártjával összekötünk, akkor a két elem inverz viszonyban (tehát n és m) nem tartozik bele a reláció aszimmetrikus részébe. Ennek alapján Suzumura társaival javasolta bevezetni a reláció konzisztens lezártja reláció fogalmát [Bosse]$\concept{CONCISTENT\_CLOSURE}\equiv \rel{R}^{\times}(m,n) \defi \forall m\forall n(\rel{R}(m,n) \lor (\rel{R}^{+}(m,n) \land \rel{R}(n,m)))$
reláció konzisztens lezártja (hun) – consistent closure relation (eng)
Az $\rel{R}^{\times}(m,n)$ relációra támaszkodva már kimondható és bizonyítható a tétel, miszerint egy reláció akkor konzisztens, ha megegyezik a konzisztens lezártjával.Relációalgebra
Minden formális elmélet számára kiemelten fontosak a relációs fogalmak, hiszen a relációk mint predikátumok adják a kijelentéseink általánosítható ismétlődéseit, ezek biztosítják kijelentéseink univerzális jellegét, ezek az állításaink "igéi". A struktúra, a strukturáltság fogalma is a relációra épül rá. Egy ilyen központi fogalom esetében is keresni lehet további absztrakciós lehetőségeket. Felmerül a kérdés: lehet-e a relációk és műveleteik között valamilyen ismert matematikai struktúrát találni? A válasz igenlő, van egy ilyen absztrakt stuktúra, amit relációalgebrának neveznek. A reláció és a köztük végezhető műveletek fogalmaira támaszkodva definiálták ezt a struktúrát. Ez azért fontos, mert az algebra egy alaposan leírt és nagyon erős tulajdonságokkal rendelkező matematikai struktúra. A matematika nagyon sok mindent tud egy struktúrára nézve mondani, ha kiderül, hogy az algebra. Vigyázni kell azonban, hogy ne tévesszük össze a relációs algebrával, ami a relációs adatbázis-kezelés matematikai alapjait biztosító elmélet. A relációalgebra felépítéséhez a következő relációs fogalmakból álló nyelvre van szükségünk.$\mathscr{L}_{RA}$($\rel{R,P,Q}, \rel{U}, \rel{E}, \rel{I}, \rel{D}, \lnot, \land, \to, =, \rel{R}^{- 1}, \overline{\rel{R}}, \times, +, \divideontimes, \dagger)$
| $\rel{R,P,Q}$ | relációk |
| $\underline{\rel{F}}$ | teljes reláció |
| $\underline{\rel{E}}$ | üres reláció |
| $\underline{\rel{I}}$ | azonosság reláció |
| $\underline{\rel{D}}$ | különbözőség reláció |
| $\lnot$ | tagadás logikai művelet |
| $\land$ | konjunkció logikai művelet |
| $\to$ | kondicionális logikai művelet |
| = | egyenlőség reláció |
| $\rel{R}^{- 1}$ | relációkonvertálás művelet |
| $\overline{\rel{R}}$ | relációkomplementálás művelet |
| $\times$ | relációmetszés művelet |
| $+$ | relációegyesítés művelet |
| $\divideontimes$ | relációszorzás művelet |
| $\dagger$ | relációösszeadás művelet |
$(\rel{R}=\rel{P} \land \rel{R}=\rel{Q}) \to \rel{P}=\rel{Q}$
$\rel{R}=\rel{P} \to (\rel{R}+ \rel{Q}=\rel{P}+ \rel{Q} \land \rel{R} \times \rel{Q}=\rel{P} \times \rel{Q})$
$\rel{R}+ \rel{Q}=\rel{Q}+ \rel{R} \land \rel{R} \times \rel{Q}=\rel{Q} \times \rel{R}$
$(\rel{R}+ \rel{P}) \times \rel{Q}=\rel{R}\times \rel{Q}+ \rel{P} \times \rel{Q} \land (\rel{R} \times \rel{P})+ \rel{Q}=(\rel{R}+ \rel{Q}) \times (\rel{P}+ \rel{Q})$
$\rel{R}+ \underline{\rel{E}} =\rel{R} \land \rel{R} \times \underline{\rel{F}}=\rel{R}$
$(\rel{R}+ \overline{\rel{R}}= \underline{\rel{F}}) \land (\rel{R} \times \overline{\rel{R}}=\underline{\rel{E}})$
$\lnot \underline{\rel{F}} = \underline{\rel{E}} \;\land\;$
$\underline{\rel{F}}= \lnot \underline{\rel{E}}$
$(\rel{R}^{- 1})^{- 1}=\rel{R}$
$(\rel{R} \divideontimes \rel{Q})^{- 1}=\rel{R}^{- 1} \divideontimes \rel{Q}^{- 1}$
$\rel{R} \divideontimes (\rel{P} \divideontimes \rel{Q})=(\rel{R} \divideontimes \rel{P}) \divideontimes \rel{Q}$
$\rel{R} \divideontimes \underline{\rel{I}}=\rel{R}$
$\rel{R} \divideontimes \underline{\rel{F}}=\underline{\rel{F}} \;\land\;$
$\underline{\rel{F}} \divideontimes \overline{\rel{R}}= \underline{\rel{F}}$
$((\rel{R} \divideontimes \rel{P}) \times \rel{Q}^{- 1}= \underline{\rel{E}}) \to ((\rel{P} \divideontimes \rel{Q}) \times \rel{R}^{- 1}=\underline{\rel{E}})$
$\underline{\rel{D}} = \overline{\underline{\rel{I}}}$
$\rel{R} \dagger \rel{Q}=\overline{\overline{\rel{R}} \divideontimes \overline{\rel{Q}}}$
Kategoriális logika
A kategoriális logika részben a predikátumlogika egyfajta előzményének, részben a predikátumlogikával párhuzamosan fejlődő, azzal részleges átfedésben levő logikai diszciplinának tekinthetjük. A kategoriális logika a kategorikus ítéletek logikai összefüggéseivel foglalkozik. Arisztotelész dolgozta ki az alapjait. A logika két fő kategóriája a szubjektum és a predikátum. Mivel ezek a terminusok más kontextusokban – legalább részben – más jelentéssel bírnak, ezért itt minősítő jelzőket kapcsolok hozzájuk, és a kategoriális szubjektum és a kategoriális predikátum fogalmát fogom definiálni. A meghatározások előtt azonban tisztázni kell azt a kérdést, mi a kategoriális logika viszonya a predikátumlogikához. A predikátumlogika az általánosabb, mivel bármilyen predikátum használatát megengedi, ezért a kijelentések belső szerkezete is tetszőleges lehet. Vehetünk egy három-argumentumú predikátumot, amit három individuumnév behelyettesítésével lehet megítélhető állítássá formálni.elad(x,y,v,w) + 'Laci', 'Zoli', 'BMW' – 'Laci eladta Zolinak a BMW-jét.'
A kategoriális logika speciálisabb, mert nem enged meg bármilyen mondatstruktúrát. Ahogy már említettem, kétféle kategóriát enged meg, a szubjektumot és a predikátumot, és ezeket csak speciális állításszerkezetekbe engedi 'beletenni". Például:Minden veréb van madár.
Ez egy lehetséges kategoriális állítás, és az egyik legfontosabb minősége az, ami a magyar nyelvben "láthatatlan": két kategória közti kopulával (a magyar nyelvben elhagyott 'van'-nal) azt fejezzük ki, hogy a két kategória (illetve azok terjedelmébe eső előfordulások) között valamilyen ontológiai kapcsolat van. A kategoriális szubjektumról állítjuk azt, hogy annak valamilyen köze van a kategoriális predikátumhoz. A kategoriális logikában két kategóriát kapcsolatára mondunk valamit úgy, hogy valamilyen módon (mennyiségileg vagy minőségileg) módosítani lehet a kategóriákat, de a két kategóriát mindenképpen a kopulával kapcsoljuk össze.$\concept{CATEGORICAL\_SUBJECT}\equiv\concept{LOGICAL\_CONSTANT}\equiv\concept{INDIVIDUAL\_NAME}\equiv\rel{S}$
kategoriális szubjektum (hun) – categorical subject (eng)
$\concept{CATEGORICAL\_PREDICATE}\equiv\concept{RELATION}\equiv\concept{FUNCTION}\equiv\rel{P}$
kategoriális predikátum (hun) – categorical predicate (eng)
A kategoriális szubjektum az, amire a kategoriális kijelentés szerkezetén belüli másik kategória, a kategoriális predikátum vonatkozik, a kategoriális predikátum pedig az, amivel a kategoriális kijelentés szerkezetén belüli másik kategóriára, a kategoriális szubjektumra vonatkozóan állítunk valamit. Az nyilvánvaló, hogy a kategoriális predikátum a predikátumlogikai értelemben felfogott predikátum fogalma alá sorolható, a kérdés az, hogy mit mondhatunk a kategoriális szubjektumra vonatkozóan. A válaszhoz tudnunk kell, hogy ilyen szerkezeti feltételek tehetünk szinguláris állításokat, amikor a szubjektum egy individuum neve, illetve általános állításokat, amikor a szubjektum valamilyen predikátumlogikai értelemben vett predikátum. Rögzítenünk kell tehát, hogy mind a kategoriális szubjektum, mind a kategoriális predikátum lehet "hagyományos" predikátum. A kategoriális logika kidolgozásakor és továbbépítésekor azonban nem ez a kérdés foglalkoztatta a logikusokat. Kezdetekben két szempont szerint osztották fel a kategoriális kijelentéseket, és ez alapján tettek meg fontos – évezredeken át fenntartott – állításokat. Egyfelől figyeltek arra, hogy partikuláris vagy univerzális állításról van-e szó, a másik szempont szerint pedig azt nézték, hogy az állításba az adott kategóriákat állító vagy tagadó módban vették-e föl. Az univerzális kijelentések a kategória terjedelmébe sorolt minden előfordulásra vonatkoztak, míg a partikuláris kijelentések hatóköre csak néhány ilyen elemre irányult. Az állító, pozitív vagy megerősítő kijelentésekben a kopula szerepelt a kategóriák között, míg a tagadó, negatív kijelentésekben a negált, tagadott kopula. A négyféle kijelentést az alábbi táblázatba rendezhetjük:| kijelentéstípus | jele | latin mondat | magyar mondat | |||||||||||
| egyetemes állító | $\rel{(A)}$ | Omne S est P. | Minden S [van] P. | |||||||||||
| egyetemes tagadó | $\rel{(E)}$ | Nullum S est P. | Egyetlen S sem P. | |||||||||||
| partikuláris állító | $\rel{(I)}$ | Quoddam S est P. | Néhány S [van] P. | |||||||||||
| partikuláris tagadó | $\rel{(O)}$ | Quoddam S non est P. | Néhány S nem P. | |||||||||||
$\concept{UNIVERSAL\_AFFIRMATIVE\_PROPOSITION}\equiv\rel{S}\rel{(A)}\rel{P}\equiv\rel{(A)}\defi\forall m (\rel{S}(m)\to \rel{P}(m))$
egyetemes állító kijelentés (hun) – universal affirmative proposition (eng)
$\concept{UNIVERSAL\_NEGATIVE\_PROPOSITION}\equiv\rel{S}\rel{(E)}\rel{P}\equiv\rel{(E)}\defi\forall m (\rel{S}(m)\to \lnot\rel{P}(m))$
egyetemes tagadó kijelentés (hun) – universal negative proposition (eng)
$\concept{PARTICULAR\_AFFIRMATIVE\_PROPOSITION}\equiv\rel{S}\rel{(I)}\rel{P}\equiv\rel{(I)}\defi\exists m (\rel{S}(m)\to \rel{P}(m))$
partikuláris állító kijelentés (hun) – particular affirmative proposition (eng)
$\concept{PARTICULAR\_NEGATIVE\_PROPOSITION}\equiv\rel{S}\rel{(O)}\rel{P}\equiv\rel{(O)}\defi\exists m (\rel{S}(m)\to \lnot\rel{P}(m))$
partikuláris tagadó kijelentés (hun) – particular negative proposition (eng)
Logikai négyszög
A kategoriális logika alapjait Arisztotelész fektette le, de ő még nem rajzolt ábrákat. Pár évszázad múlva Apuleius, majd Boethius volt az, aki a négyféle kijelentés közti kapcsolatokat ábrában kezdte mutatni. Az ilyen az ábrákat szokták Apuleius négyszögének vagy Boetius-féle négyzetnek is nevezni, de ezeken túl gyakran használják még a logikai négyszög, a logikai négyzet, valamint az ellentétek négyszöge vagy az oppozíciós négyszög kifejezéseket is [Jean-] [Aless] [♦] Az ábra így néz ki: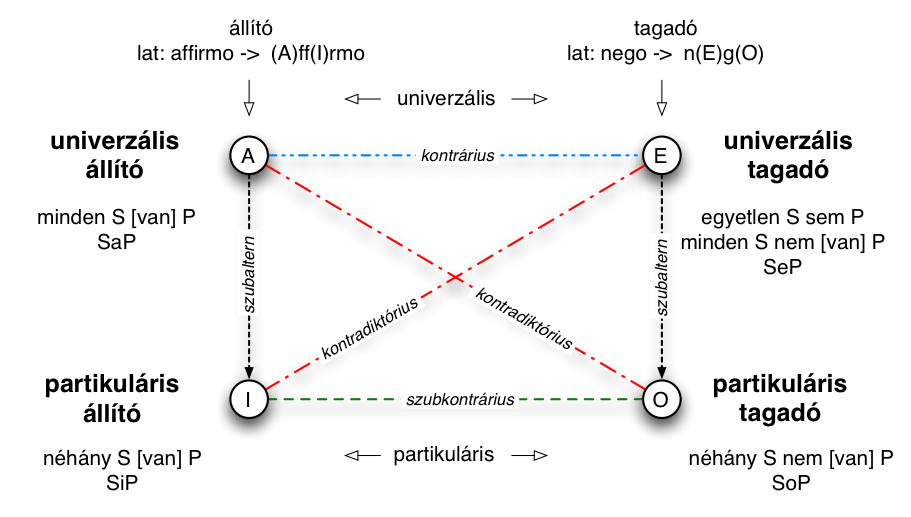
A négyszög négy sarokpontját elnevezték ($\rel{(A)}$-, $\rel{(E)}$-, $\rel{(I)}$-, $\rel{(O)}$-pontoknak), és így hivatkoznak rájuk a mai napig. Az ábrán már feltüntettem, de az eddigiekből még nem derült ki, miért is nevezték ellentétek négyszögének ezt az alakzatot. Ugyan Arisztotelész nem használta még ezt a fenti vizuális megjelenítést, azonban ő volt az, aki alaposan leírta a kijelentések közti viszonyrendszert, és kiderült, a kijelentéstípusok közti kapcsolatok majd mindegyike valamifajta ellentétet fejez ki. A logikai négyzet elemei közt évszázadokon keresztül három ellentétes viszonyt tételeztek: (i) a kontradiktórius (ellentmondó), (ii) a kontrárius (ellentétes), valamint (iii) a szubkontrárius (alárendelt ellentétes) kapcsolatot. Ezeken felül rögzítettek még egy alárendeltségi viszonyt kifejező szubaltern (alárendelt), szuperaltern (fölérendelt) kapcsolatpárt is. Ezen kapcsolatokat, illetve modernkori megfelelőiket az alábbi táblázat mutatja.
| ellentét | formulája | logikai művelet neve | jele | |||||||||||
| szubkontrárius | $\lnot(\lnot A\land\lnot B)$ | diszjunkció | $A\lor B$ | |||||||||||
| kontradiktórius | $\lnot(A \land B) \land \lnot(\lnot A \land \lnot B)$ | biszubtrakció | $A \not\leftrightarrow B$ | |||||||||||
| kontrárius | $\lnot(A \land B)$ | exklúzió | $A \not\land B$ | |||||||||||
| szubaltern | $A \rightarrow B$ | implikáció | $A \rightarrow B$ | |||||||||||
| $\rel{(A)}$ | $\rel{(E)}$ | $\rel{(I)}$ | $\rel{(O)}$ | |||||||||||
| alethikus logika | szükségszerű | lehetetlen | lehetséges | nem-szükségszerű | ||||||||||
| deontikus logika | kötelező | tilos | megengedett | nem-kötelező | ||||||||||
Logikai hatszög
A logikai négyzettel kapcsolatban felmerültek másfajta problémák is, ezek azonban sokkal inkább a továbbfejlesztési lehetőségek keresésére ösztönözték a kutatókat, mint a négyszög-gondolat feladására. A négyszög hatszögesítését Augustin Sesmat és Robert Blanché egymástól függetlenül, közel egyidőben végezte el az 1950-es években, de közel ötven éven keresztül eredményeiknek nem volt jelentős hatása a tudományos gondolkozásra. Csak a 2000-es években változott ez a helyzet [Jean-] Kiderült, hogy a logikai négyzet négy sarokpontja egyszerre volt kevés is és sok is a tényleges összefüggések pontos megragadására. Zavaró volt, hogy a hétköznapi és a tudományos-logikai nyelvhasználat több ponton eltért egymástól. Az $\rel{(I)}$-sarokba tartozó kategóriákat sokszor az $\rel{(A)}$-sarokba tartozó kategóriákkal ellentétesnek érezzük, szemben a logikai négyzet "állításával", mely szerint a két pont állításai között szubaltern viszony létezik, ami egyáltalán nem számít ellentétes kapcsolatnak (a megengedett vagy a lehetséges fogalmát sokszor sokkal inkább érezzük ellentétesnek, mint alárendeltnek a kötelező vagy a szükségszerű fogalmához képest). Magyarázatra szorult az a furcsa tény is, hogy az $\rel{(O)}$-pontba került kategóriáknak szinte sosem volt megfelelő hétköznapi terminusa. A modális logikában például a nem-szükségszerű, nem-kötelező "mesterséges" terminusokat kellett használni a hiányzó természetes szavak hiányában. Az ilyen és ehhez hasonló problémák feloldhatónak látszottak azáltal, hogy két új pólust veszünk fel a négyzethez, és ezáltal olyan logikai hatszöghöz jutunk, amely két háromszögből áll. Első lépésként az "eredeti" logikai négyszög helyett érdemesebb egy olyan logikai háromszöget képezni, amelyben megmarad az $\rel{(A)}$- és az $\rel{(E)}$-sarok, és ezek mellé kell egy új pólust felvenni. Ezt az új pólust – Blanché után – $\rel{'Y'}$ karakterrel kezdték el jelölni. Az az új logikai háromszög nagyon hasznosnak ígérkezett. Egyre több olyan fogalomhármast kezdtek felfedezni a gondolkodás, a kategóriaképzés legkülönfélébb területein, amelyek mind egyidejű igazságukat kölcsönösen kizáró, tehát kontrárius háromszöget alkottak egymással. Íme néhány példa.| $\rel{(A)}$ | $\rel{(E)}$ | $\rel{(Y)}$ | ||||||||||||
| kvantifikáció | minden | semmi | valami | |||||||||||
| tér | mindenhol | sehol | valahol | |||||||||||
| idő | mindig | soha | valamikor (néha) | |||||||||||
| alethikus modaitás | szükségszerű | lehetetlen | kontingens | |||||||||||
| deontikus modalitás | kötelező | tiltott | megengedett | |||||||||||
$\concept{UNIVERSAL\_PROPOSITION}\equiv\rel{S}\rel{(U)}\rel{P}\equiv\rel{(U)}\defi\rel{(A)}\lor \rel{(E)}$
egyetemes kijelentés (hun) – universal proposition (eng)
$\concept{PARTICULAR\_PROPOSITION}\equiv\rel{S}\rel{(Y)}\rel{P}\equiv\rel{(Y)}\defi\rel{(I)} \land \rel{(O)} $
partikuláris kijelentés (hun) – particular proposition (eng)
Az új elemek felvétele után felvetődik a kérdés, vajon milyen összefüggések léteznek az új (és régi) kategóriák között. Kiderült, hogy a már jelzett kapcsolatokon túl a szubaltern relációk még több sarokpont között behúzhatóak, ahogy az a következő ábra mutatja.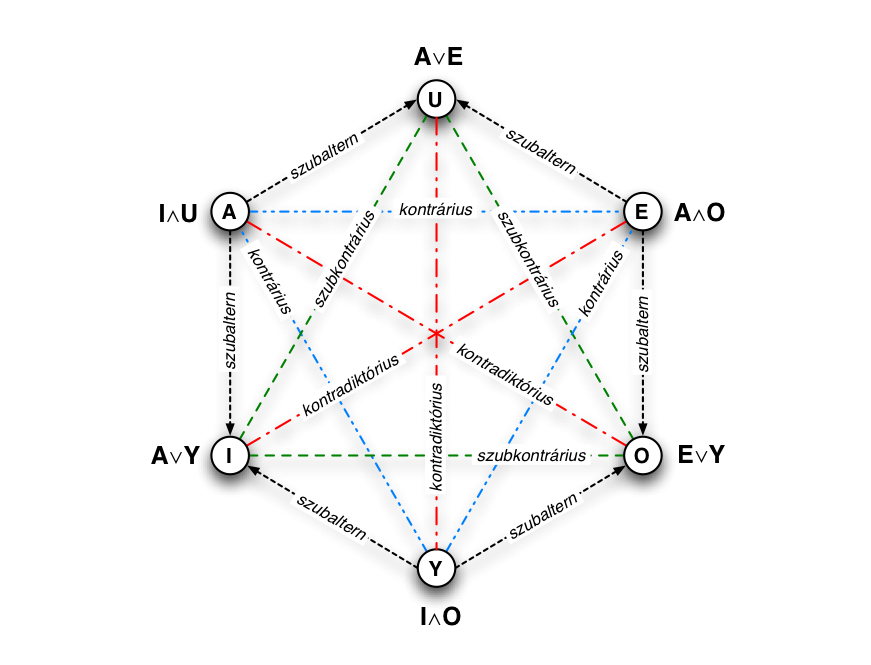
A hatszög kapcsolatrendszerét felvázolva észrevehetünk még egy további rejtett összefüggést is. A hatszögbe nemcsak egy, hanem összesen három négyszög van "elrejtve", és a két "új" négyszög ugyanolyan belső szerkezettel rendelkezik, mint az "eredeti" logikai négyszög. Az ellentétes pólusaikban kontradiktórius, a szomszédos sarokpontok közt kontrárius vagy szubkontrárius, valamint szubaltern viszonyokat találhatunk. A három négyszöget kiemeltem a hatszögből és eredeti helyzetüket megtartva mutatom be őket.
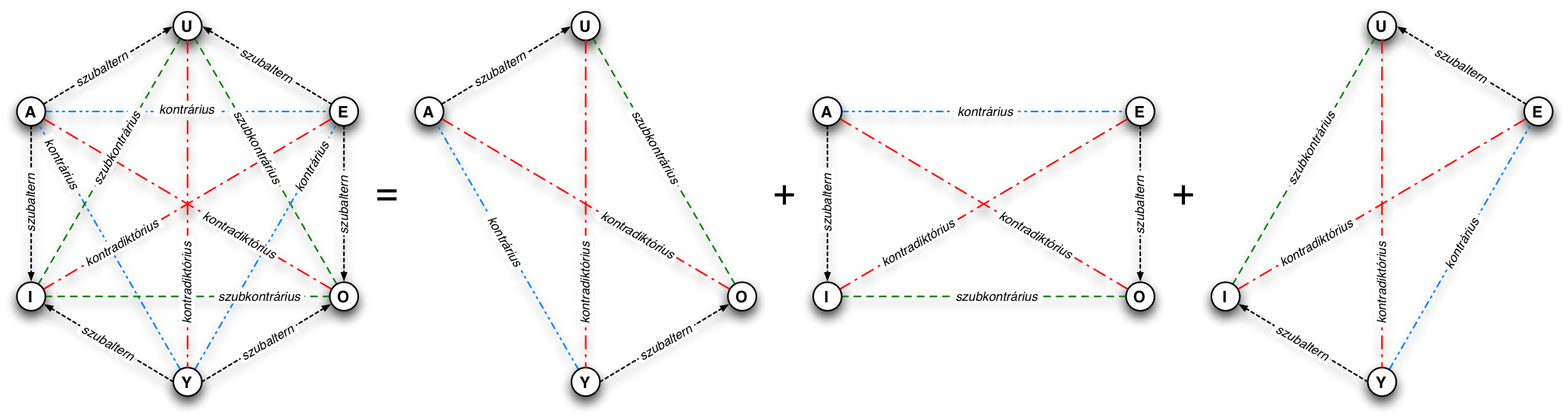
Idővel kiderült, hogy a logikai hatszög sok területen használható. A logikai operátorokat vizsgálva Blanché rájött arra, hogy a tíz legfontosabb operátor ábrázolható két logikai hatszög segítségével. A nullad- és az elsőrendű operátorok (a tautológia és ellentmondás, valamint a négyféle projekciós művelet) nélkül marad tíz műveletünk, ezek a "tisztán" másodrendű logikai operátorok, és ezeket rendezte Blanché egy összefüggő szerkezetbe.
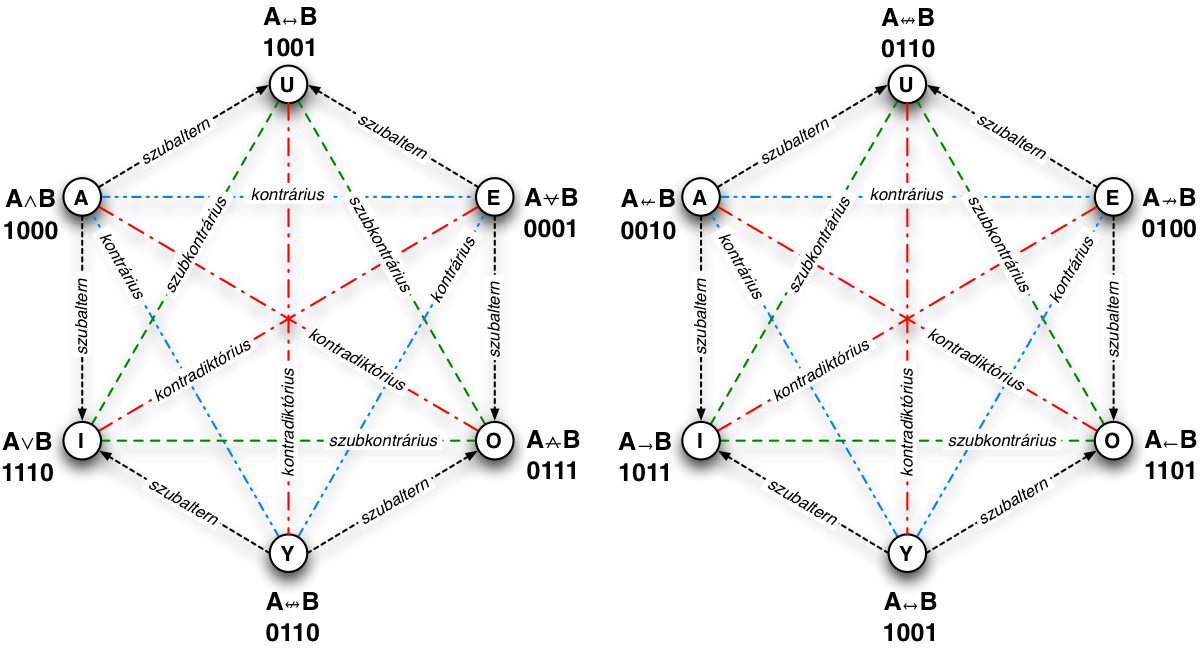
A geometriai szemlélet érvényesítését, további hasznosítását azonban itt már nem lehetett leállítani. [♦] Amíg a logikai operátorok egymáshoz való viszonyát Blanché még úgy fejezte ki, hogy az operátorok közül tizet két hatszögbe foglalt bele, addig Sauriol már mind a tizenhat operátort egyetlen alakzatban tudta "megmutatni" egy tetrahexahedron segítségével. A tetrahexahedron egy kockából és hat darab piramisból álló geometriai forma, aminek a drótváza hat darab hatszögből is összeállítható. Ezt meg lehet jeleníteni háromdimenziós formában, és hogy könnyebben felismerhetők legyenek a benne "rejtőző" hatszögek, egyenként kiemelve őket megmutatom a helyzetüket is a tetrahexahedronon belül.
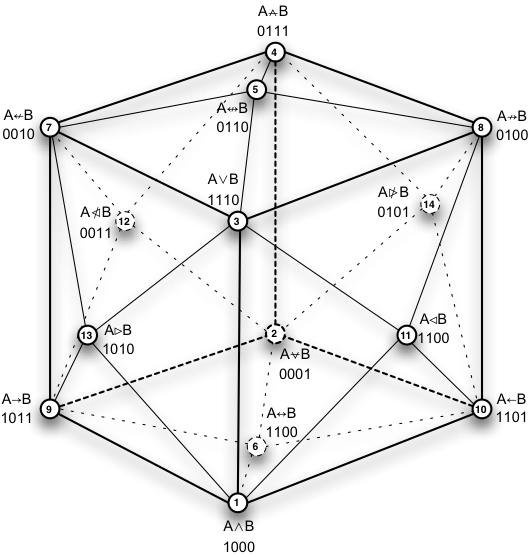
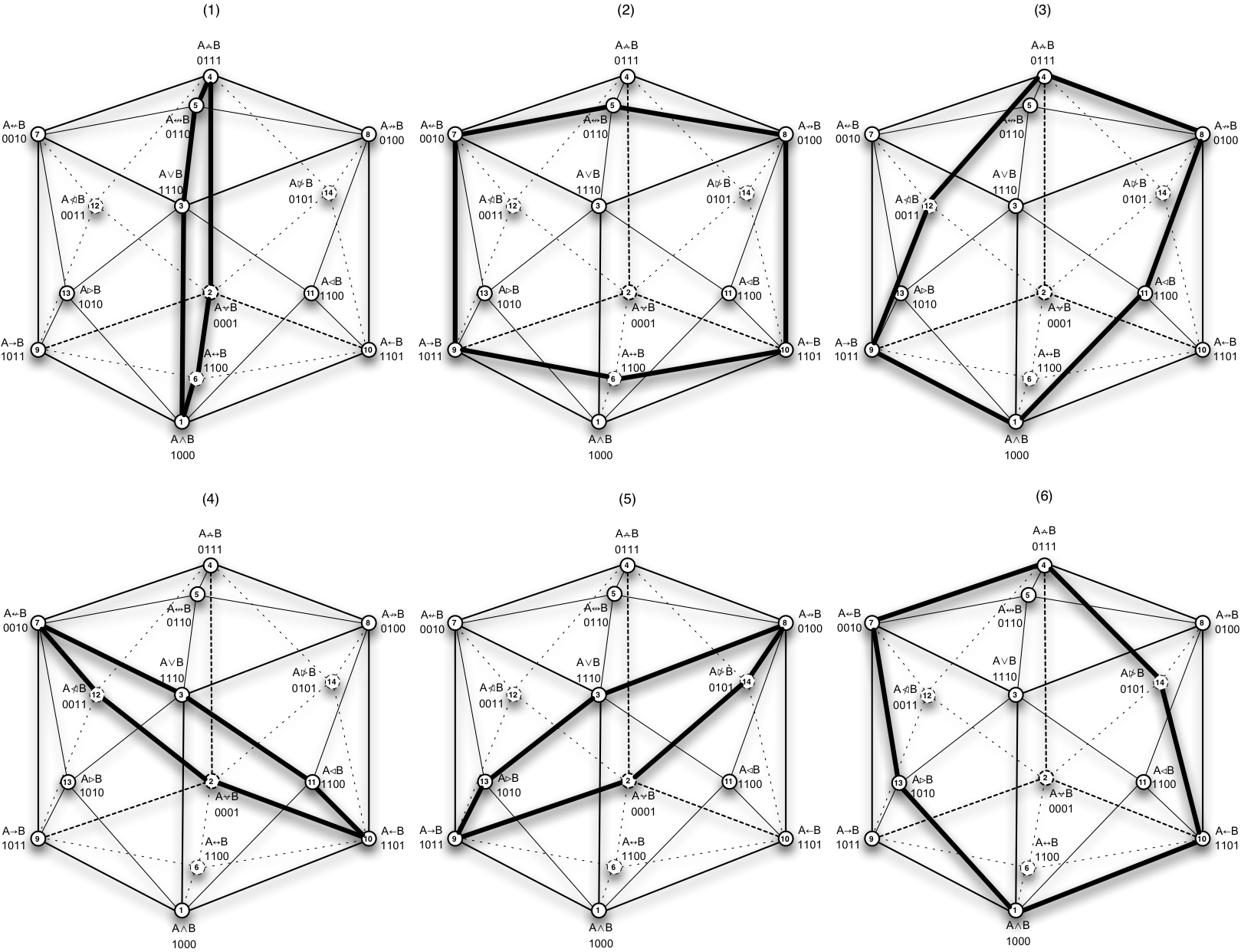
A logikai hatszögek, majd a további geometriai formák alkalmazhatósága sikere bizonyos értelemben "kijelölte" a továbblépési lehetőségeket a geometriai általánosítás irányába, és megjelentek azok a cikkek, amelyek logikai n-szögekről és a problémakör geometrizálásáról szóltak [Aless] [Aless] Ezekkel azonban itt nem foglalkozom.
Közvetlen következtetések, átalakítási műveletek kategoriális kijelentések esetén
A logika négyszög kapcsán is sokat foglalkoztak a kategoriális kijelentések átalakítási lehetőségeivel. Azért volt mindez fontos, mert ezek olykor közvetlen következtetési szabályként is működtek [Rober] Előre fontos hangsúlyozni, hogy ezek az átalakítási szabályok nem mindig eredményeznek igaz állításból igaz állítást, tehát nem minden esetben működnek következtetési szabályként. Ahhoz, hogy mind a négy kategorikus állítástípusra egyszerre megfogalmazhassuk majd az átalakítási szabályokat, illetve az érvényes következtetési formulákat, érdemes bevezetni a $\rel{(C)}$ általános kategorikus propozíció fogalmát. Ebből persze egyből kettőt kell definiálnunk, hogy – szükség esetén – jelezni tudjuk, melyik esetről teszünk állítást, négy vagy hat típusról, a logikai négyszög vagy a logikai hatszög elemeiről beszélünk.$\concept{GENERAL\_C-PROPOSITION}\equiv\rel{S}\rel{(C)}_4\rel{P}\equiv\rel{(C)}_4\defi \rel{(A)}\veebar\rel{(E)}\veebar\rel{(O)}\veebar\rel{(I)}$ $\concept{GENERAL\_C-PROPOSITION}\equiv\rel{S}\rel{(C)}_6\rel{P}\equiv\rel{(C)}_6\defi \rel{(A)}\veebar\rel{(E)}\veebar\rel{(O)}\veebar\rel{(I)}\veebar\rel{(U)}\veebar\rel{(Y)}$
Az új fogalom bevezetésének csak annyi értelme van, hogy segítségével egyszerűsíthetünk a későbbi definíciókon. A fogalomnak önálló szemantikája nincs, csak egy belső mintázattal rendelkező változóként érdemes felfogni. A korábban már bevezetett átalakítási műveleteket itt – igaz, új értelmezési tartományon – újraértelmezhetjük. A konverzió meghatározásában a korábbiakhoz képest (☜) csak annyi változásra van itt szükség, hogy az értelmezési tartományt le kell szűkíteni a kategoriális kijelentések halmazára. A műveletet az általános kategoriális propozícióváltozó segítségével definiálhatjuk.$\concept{C-CONVERSION}\equiv\rel{S}\rel{(C)}_4^{- 1}\rel{P}\equiv\rel{(C)}_4^{- 1}\defi\forall m(\rel{S}\rel{(C)}_4^{- 1}\rel{P}\leftrightarrow \rel{P}\rel{(C)}_4\rel{S})$
kategoriális konverzió (hun) – category conversion (eng)
A kategoriális konverzió olyan konverzió, amelynek értelmezési tartománya a kategoriális kijelentések halmaza. A kategoriális konverzió praktikusan annyit tesz, hogy a kijelentésben felcseréljük a szubjektumot és a predikátumot. Ha a tradicionális oppozíciós négyzet $\rel{(E)}$-propozíciója ('Egyetlen S sem P.') igaz, akkor annak megfordítása ('Egyetlen P sem S.') is igaz, tehát ez a konverzió közvetlen következtetési szabályként is alkalmazható. Ugyanúgy elmondható ez az $\rel{(I)}$-propozícióra is ('Néhány S [van] P.'), mert annak a megfordítása ('Néhány P [van] S.') megintcsak igaz. A négyzet másik két állítása is megfordítható, de ezekben az esetekben nem áll fenn a konverz kijelentések igazsága. Az átalakítási műveletek korábbi tárgyalásakor nem mutattam be az obverzió műveletét, mert ez igazából csak a kategoriális kijelentések esetében értelmezhető. Az új művelet bevezetéséhez szükség van a kategóriák (relációk) komplementumaira is, és a kategoriális predikátum tagadására.$\concept{OBVERSION}\equiv\rel{S}\rel{(C)}_4^{- o}\rel{P}\equiv\rel{(C)}_4^{- o}\defi \forall m(\rel{S}\rel{(C)}_4^{- o}\rel{P}\leftrightarrow\overline{\rel{S}}\rel{(C)}_4\lnot \overline{\rel{P}})$
obverzió (hun) – átalakítás (hun) – category obversion (eng)
Az obverzió olyan átalakítási művelet, [♦] ami megtartja a szubjektum és predikátum sorrendjét, de kicseréli őket a komplementumaira, valamint a predikátum komplementumát tagadva állítja. A propozicionális logikában az obverzió műveletét nem használják. Vélhetőleg azért nem, mert az állításlogikában hiányzik a pozitív és negatív (állító és tagadó) kijelentések megkülönböztetése, ami viszont a kategoriális logikában adott. A kategoriális kijelentések színterén is értelemezhető a kontrapozíció művelete, ami itt kifejezhető a konverzió és obverzió segítségével is. Ezt azonban akkor lehet jól szemléltetni, ha használjuk a részleges kontrapozíció műveletét.$\concept{PARTIAL\_C-CONTRAPOSITION}\equiv\rel{S}\rel{(C)}_4^{- r}\rel{P}\equiv\rel{(C)}_4^{- r}\defi \forall m(\rel{S}\rel{(C)}_4^{- r}\rel{P}\leftrightarrow\lnot\overline{\rel{P}}\rel{(C)}_4\overline{\rel{S}})$
részleges kategoriális kontrapozíció (hun) – partial category contraposition (eng)
A részleges kategoriális kontrapozíció az a művelet, amely egyszer-egyszer alkalmazza az obverzió és a konverzió műveletét. A művelet "képlete" tehát egyszerű: részleges kontrapozíció = átalakítás + megfordítás.$\concept{C-CONTRAPOSITION}\equiv\rel{S}\rel{(C)}_4^{- p}\rel{P}\equiv\rel{(C)}_4^{- p}\defi \forall m(\rel{S}\rel{(C)}_4^{- p}\rel{P}\leftrightarrow\lnot\rel{P}\rel{(C)}_4\lnot\rel{S})$
teljes kategoriális kontrapozíció (hun) – kategoriális kontrapozíció (hun) – categoric contraposition (eng)
A teljes kategoriális kontrapozíció olyan kontrapozíció, amelynek az értelmezési tartománya a kategoriális kijelentések halmaza. A kategoriális kontrapozíció praktikusan annyit tesz, hogy megcseréli a kijelentés szubjektumának és predikátumának komplementumait. A művelet felírható a következő alakban is: kategoriális kontrapozíció = átalakítás + megfordítás + átalakítás.$(\rel{(C)}_4=\rel{(A)}\veebar\rel{(C)}_4=\rel{(O)})\to(\concept{C-CONTRAPOSITION}\leftrightarrow \concept{OBVERSION}(\concept{C-CONVERSION}(\concept{OBVERSION})))$
A kondicionális alak azt jelzi, hogy a fenti formula nem minden esetben igaz: a négyből csak két esetben. Ha az $\rel{(A)}$-propozíció igaz, akkor annak kategoriális kontraponáltja is igaz, tehát ez az átalakítás használható közvetlen következtetési szabályként. Ugyanez áll az $\rel{(O)}$-propozícióra is, hiszen a kontraponáltja igaz. A relációműveletek között szerepelt az inverzió is. Ezt is definiálhatjuk itt, bár a jelentősége, hasznossága kisebb a többi átalakítási szabályhoz képest. A definíciót így adhatjuk meg:$\concept{C-INVERSION}\equiv\rel{S}\rel{(C)}_4^{- i}\rel{P}\equiv\rel{(C)}_4^{- i}\defi \forall m(\rel{S}\rel{(C)}_4^{- i}\rel{P}\leftrightarrow\overline{\rel{S}}\rel{(C)}_4\overline{\rel{P}})$
kategoriális inverzió (hun) – category inversion (eng)
A kategoriális inverzió az a művelet, amelynek az értelmezési tartománya a kategoriális kijelentések halmaza. A kategoriális inverzió kicseréli a kijelentés két kategóriáját azok komplementjeire, de megtartja a sorrendjüket. Az inverziónak nincs direkt következtetési potenciálja.JEPD-elv
Amikor elméleti modellt építünk, akkor a generikus alárendeltje reláció segítségével képzünk új fogalmakat úgy, hogy egy már definiált fogalom alá egy tulajdonságnyaláb segítségével szűkebb terjedelmű, viszont bővebb jelentésű alosztályfogalmakat rendelünk. Az alosztály (altípus, faj) fogalmak képzésekor sokdszor érdemes törekednünk arra, hogy igazodjunk a JEPD-elv elvárásaihoz [Thoma] Ez az elv azt rögzíti, hogy egy fogalom alá rendelt fogalmak együttesen kimerítőek legyenek és kölcsönösen kizárják egymást (JEPD – Jointly Exhaustive and Pairwise Disjoint). [♦] A generikus struktúra konzisztenciájához nélkülözhetetlen vagy legalábbis fontos, hogy az azonos fogalmi szinten egymás mellett levő, egy közös fölérendelt kategóriához tartozó fogalmak tartalma kölcsönösen kizáró és együttesen kimerítő legyen. Ezáltal elégíthetjük ki azt az elvárást, hogy egy adott fogalom alá kidolgozott fogalmak együttesen a fogalom terjedelmébe tartozó minden előfordulást egyértelműen lefedjenek. A matematika világából a JEPD-elvnek megfeleltethető egy osztály alatt létrehozott alosztályokból történő partíció képzése. Ebben az esetben is az az elvárás, hogy az alosztályok egyetlen példányt tekintve se fedjék át egymást (vagyis az alosztályok partíciók legyenek), illetve az alosztályok terjedelmükkel teljes mértékben lefedjék a fölöttes osztályfogalom (szülőosztály) terjedelmét (vagyis a partíció teljes legyen). Ez ugyanazt jelenti, mint amit a halmazelméletben a partíció (partition) fogalma a halmaz és részhalmazai közti viszonyban (☜) Ha egy fogalom alá olyan generikusan alárendelt fogalmakat hozunk létre, amelyek kielégítik a JEPD-elv elvárásait, akkor azt mondhatjuk, hogy a fogalmat particináltuk, partíciókra bontottuk fel. A JPED-elv érvényesül például a logikai hatszög azon kategóriái között, amelyek kontrárius viszonyban állnak egymással, vagyis az $\rel{(A)}$, az $\rel{(E)}$ és az $\rel{(Y)}$ kategóriák között. Nem teljesül viszont a logikai négyszög elemeire.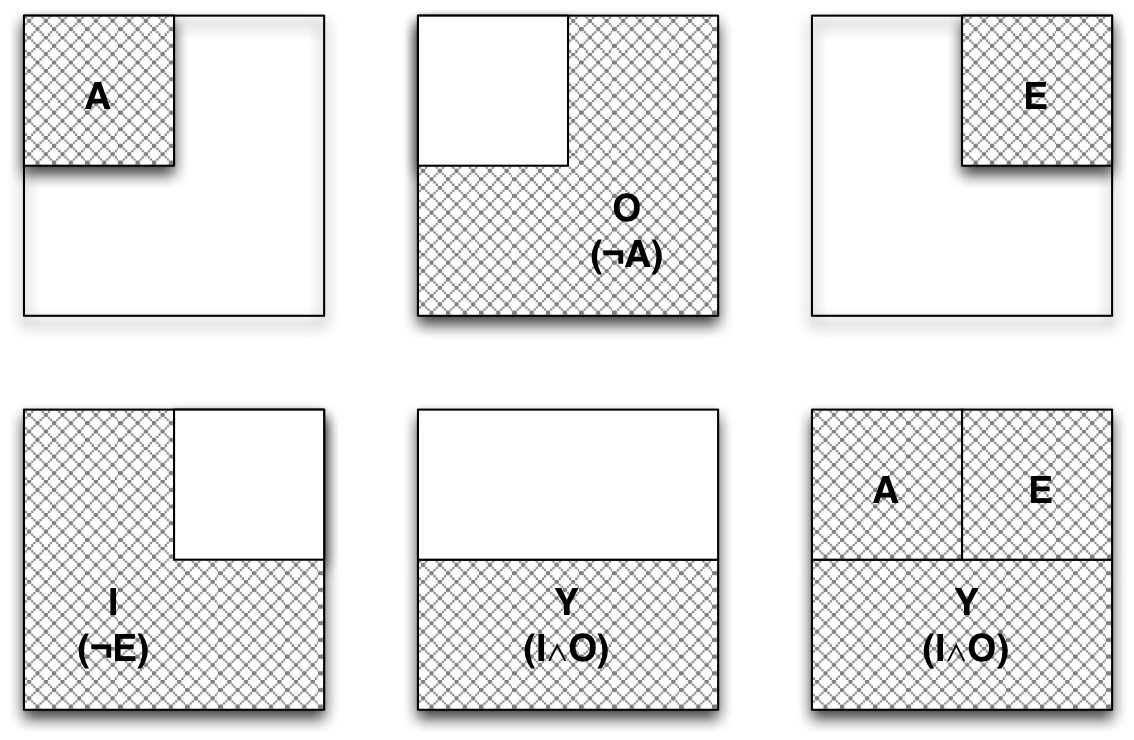
A logikai hatszög bevezetése ezért is fontos, mert ezáltal olyan kategóriafelosztáshoz juthatunk, amely partíciónak minősül, vagyis érvényes rá a JEPD-elv. A későbbiek során, amikor csak lehet, alkalmazni fogom a JEPD-elvet. Az elméleti építkezés során mindig fontos annak tisztázása, vajon a fogalmi modell bővítésekor mindent figyelembe vettünk-e. Ha ilyenkor az új fogalmakra vonatkozóan állítani lehet a JEPD-elv teljesülését, akkor az éppen adott szempont szerint teljesnek mondható az elméleti keret bővítése.
Reifikáció
Az egyértelműséggel és konzisztenciával kapcsolatos elvárások miatt említést kell tennem még egy nagyon fontos jelenségről. A relációk a világ dolgai közti kapcsolatokat fejezik ki. Ez az jelenti, hogy – bináris relációk esetén – egy relációt jelző terminussal mindig két dolog, két relátum közti viszonyt ragadunk meg. A relációfogalmak bevezetése után azonban a fogalom (terminus) használata során előfordulhat, hogy ezt a viszonyfogalmat "tárgyiasítjuk" és valamelyik relátummal megragadott "dologra" vonatkoztatjuk a fogalmat (terminust). Egy hétköznapi példával szemléltetem ezt a jelenséget. Vegyük az 'apja' relációt (terminust), ami egy közvetlen biológiai leszármazási viszonyt ír le két ember között, amikor az "örökítő" pozícióban levő egyed hímnenű. Az 'apja' tehát viszonyt fejez ki. A kommunikáció során azonban nagyon gyakran úgy használjuk ezt a fogalmat, hogy sokkal inkább arra a dologra, arra az emberre gondolunk, aki a kapcsolat egyik felét testesíti meg. Magyarul ekkor az 'apa' terminust használjuk. Amikor így teszünk, akkor reifikáljuk a relációfogalmat, a relációból kiemeljük az egyik relátumot és csak erre hivatkozunk. Természetesen nincs semmi probléma ezzel a jelenséggel, csak arra kell figyelni, hogy mindig tudjuk, éppen a relációfogalmat magát vagy épp annak származtatott változatát, a reifikátumát használjuk. Azt következményt viszont fontos figyelembe venni, hogy amikor reifikálunk egy relációt, akkor információt vesztünk, hiszen a reifikátum már nem mond semmit a reláció másik relátumáról. A reláció másik relátumát általában a reláció inverze segítségével tudjuk könnyen reifikálni.| állítás | reláció | reifikátum | inverz reláció | inverz reifikátum | ||||||||||
| Laci apja Katinak. | $apja(Laci,Kati)$ | $apa(Laci)$ | $gyereke(Kati,Laci)$ | $gyerek(Kati)$ | ||||||||||
| Laci apja Lilinek. | $apja(Laci,Lili)$ | $apa(Laci)$ | $gyereke(Lili,Laci)$ | $gyerek(Lili)$ | ||||||||||
| Zoli apja Petinek. | $apja(Zoli,Peti)$ | $apa(Zoli)$ | $gyereke(Peti,Zoli)$ | $gyerek(Zoli)$ | ||||||||||
$\concept{LEFT-REIFICATION}\equiv\concept{REIFICATION}\equiv `\rel{R}(m,n)\equiv`\rel{R}\equiv\rel{R}' \defi \forall m \forall n(`\rel{R}(m,n) \leftrightarrow \rel{R}(m))$
bal-reifikáció (hun) – reifikáció (hun) – reification (eng)
$\concept{RIGHT-REIFICATION}\equiv\concept{REIFICATION}\equiv\rel{R}'(m,n)\equiv\rel{R}' \defi \forall m \forall n(\rel{R}'(m,n) \leftrightarrow \rel{R}(n))$
jobb-reifikáció (hun) – reifikáció (hun) – reification (eng)
A reifikáció művelete – a dolgokat absztraktan szemlélve – hasonlít a propozicionális logika projekció műveleteihez (☜) hiszen itt is, ott is arról van szó, hogy két valamilyen módon összekapcsolt elem közül a művelet végrehajtása során (eredményeként) csak az egyiket vesszük figyelembe. A reifikáció műveletét még tovább absztrahálhatjuk, és tetszőleges absztrakt individuumokat létrehozhatunk, ami a tudásreprezentáció számára nagyon praktikus előnyökkel szolgálhat [Ronal] Donald Davidson az események logikai reprezentálhatóságát keresve tett egy javaslatot arra, hogy miként lehetne az eseményeket megfelelő módon logikai formulákkal leírni [Donal] A davidsoni megoldásnak van egy reifikációs vonzata is, ami az események, illetve az arra építhető cselekvések logikai leírásában nagyon jól hasznosítható. Jerry Hobbs 'Ontológiai promiszkuitás' címen írott cikkében olyan reifikációs leíró nyelvre tett javaslatot, ami Davidson ötletét vitte tovább, de annál nagyobb rugalmasságot, jobb kezelhetőséget biztosított a jelenségek logikai leírása számára [Hobbs] A davidsoni-hobbsi ajánlásokat én is megpróbálom figyelembe venni az elemzett jelenségek formális leírása során. Azt viszont jeleznem kell, hogy a reifikáció fogalmának itteni értelmezése nagyon eltér az olyan társadalomtudományi megközelítésektől, mint a Berger-Luckman-féle reifikációfelfogás vagy a Marx-féle tárgyiasulás/tárgyiasítás elméletben megtestesülő interpretáció.Másodrendű logika
Abban a pillanatban, hogy a logikai nyelvünkbe felvesszük a változókat és kvantorokat, lehetővé válik, hogy egy új szempont szerint különíthessünk el különböző logikákat, logikai szinteket. Nem véletlenül nevezik a kijelentéslogikát nulladrendű extenzionális logikának, a predikátumlogikát pedig elsőrendű logikának [Ruzsa] Mivel a kvantálás, a kvantorok alkalmazásának lehetősége a predikátumlogikában jelenik meg először, ezért ez a logikát (és ezt a logikai szintet) nevezzük elsőrendűnek. Elsőrendű logikákban a kvantorokat az individuumok valamely csoportját jelölő változókra lehet alkalmazni, semmi másra. Ha egyáltalán nem használhatunk kvantorokat (mert az adott logikában ez nincs is implementálva), akkor nulladrendű nyelvről beszélhetünk. Az ítéletlogikában nincsenek kvantorok, ezért az a logika nulladrendű. A másodrendű logikák felé úgy lehet elmozdulni, hogy kiterjesztjük a változók, illetve a kvantorok hatókörét. Ezt úgy tehetünk meg, hogy egyfelől megengedjük, hogy változókat ne csak individuumokra, hanem predikátumokra (relációkra, függvényekre) vonatkozóan is lehessen képezni, másfelől megengedjük azt is, hogy a kvantorokat az individuumváltozókon túl a predikátumokra irányuló változókra is lehessen alkalmazni [Feren] [Ruzsa] A formulák szintjén ez úgy ismerhető fel, hogy az individuumváltozók mellett a predikátumváltozókra is érvényesítjük a formulában használt kvantorokat, valahogy így: $\forall m \forall P \forall Q(P(x) \rightarrow Q(x))$ Ez a formula a generikus alárendeltje (generic subordinate) relációt definiálja, amely a predikátumok, fogalmak közti alá-fölérendeltségi viszonyt (vagy másként a faja-neme, ISA relációt) írja le. Ha a másodrendű logikában megengedett, hogy a predikátumokra, kategóriákra is alkalmazzuk a változókat és kvantorokat, akkor ez azt is jelenti egyben, hogy a fogalmi szinten is képezhetünk másodrendű fogalmakat. Ezek formálisan úgy jeleníthetők meg, hogy az adott predikátum (fogalom) változóhelyeire, a predikátum paraméterei közé olyan predikátumot (fogalmat) írunk be, amely szerepel az elsőrendű predikátumok (fogalmak) között. Ez a beágyazás egyértelműen jelzi a predikátum (fogalom) másodrendű minőségét. Ha vesszük a 'tudja, hogy' predikátumot, aminek két változóhelyet tartunk fent, amelyekkel jelölni akarjuk, hogy 'ki az, aki tud valamit', illetve 'mit tud az a valaki'. Ezt a predikátumot így definiálhatjuk.tud$(X,P)$ – X tudja, hogy P
Előfordulhat azonban az is, hogy a P paraméterre újra a 'tudja hogy' predikátumot alkalmazzuk, amikor például azt mondjuk, hogy:$P$ = tud$(Y,Q)$ – Y tudja, hogy Q
Ha a P tudásra vonatkozó második mondatunkat behelyettesítjük az első mondatba, akkor ilyen formulát kapunk:tud(X,P) = tud(X,tud(Y,Q)) – X tudja, hogy Y tudja, hogy Q
Ezen a ponton szépen látszik a predikátum önmagába való beágyazottsága. Amikor ilyet tapasztalunk, akkor mindig másodrendű fogalomról van szó, aminek leírásához már másodrendű logikára van szükség. Ilyen esetekben ugyanis ha általános kijelentéseket akarunk tenni (az univerzális kvantor használatával), akkor meg kell engednünk, hogy a változókat és kvantorokat predikátumra is lehessen alkalmazni. A hétköznapi kommunikációban és a társadalomtudományi diskurzusban egyaránt rengeteg másodrendű fogalmat használunk, igaz, reflektálatlanul. A későbbiekben mindig jelezni fogom, amikor másodrendű fogalmakhoz jutunk valamely téma tárgyalása során. Teszem ezt egyfelől a fogalmi egzaktság érdekében, de másfelől teszem ezt azért is, mert a másodrendű fogalmak használata könnyen paradoxonhoz vezet. Ha már beszélünk másodrendű logikáról, akkor természetesen beszélhetünk magasabbrendű (harmadrendű, negyedrendű stb.) logikáról is. Ezeket a másodrendű logikához hasonlóan lehet képezni. Minél magasabbrendű fogalmat képzünk, annál inkább egyre mélyebben egymásba ágyazott fogalmakhoz jutunk. A cselekvéselméleten belül gyakran kell másodrendű fogalmakat használnunk, jóval ritkábban, de azért felbukkannak harmadrendű fogalmak, viszont harmadrendnél magasabb szintre már nem nagyon kell felmennünk. A végtelen egymásba ágyazás, a tetszőlegesen magasabb rendű fogalmak elvi lehetőségét nem használjuk ki a tényleges fogalomhasználati gyakorlatunkban.Modális logika
A társadalmi cselekvés modelljének felépítése során több alkalommal is szükségünk lesz olyan elméletekre, amelyek a deontikus logika területéhez sorolhatók (már a cselekvés fogalmának értelmezéséhez is szükségünk van erre a diszciplinára). A deontikus logikát a modális logika egyik ágaként kezeljük. A modális logika nem elsősorban a kijelentések igazságának kérdéseivel, hanem inkább a kijelentések igazságának modalitásával (minőségével, "erősségével", megalapozottságával) foglalkozik. Szükségszerű-e egy kijelentés igazsága; mindig fent kell-e tartanunk a kijelentés igazságát vagy azt csak bizonyos feltételek, adott világ, világállapot létezéséhez tudjuk kötni; van-e olyan kijelentés, ami sosem lehet igaz, tehát lehetetlen; melyek azok a kijelentések, amelyek lehetségesen igazak, de nem szükségszerűek; ha valami szükségszerűen igaz, akkor igaz is-e egyben – ilyen és ezekhez hasonló kérdésekre próbál meg válaszokat találni a modális logika. [♦] Mivel sokféleképpen módosíthatjuk az állításainkat, sokféle modalitást kezelhetünk. Egy A kijelentés kapcsán mondhatjuk azt, hogy ' tudom, hogy A', 'azt hiszem, hogy A', 'gyakran A', 'biztos, hogy A', 'tilos A', 'szükségszerű, hogy A' stb. Ilyen esetekben az állításunkat (A-t) valamilyen modalitásértékkel "kiegészítjük", módosítjuk, amit úgy is kifejezhetünk, hogy az állításhoz egy modális operátort kapcsolunk hozzá. Amikor az állításaink szükségszerűségét vizsgáljuk, akkor alethikus modalitásról van szó. A normativitás, a konstruált kötelezőség világát a deontikus, a kijelentések időbeliségét a temporális, a hitek logikáját a doxasztikus, a tudásokét az episztemikus modalitással próbáljuk megragadni. A modális logika nyelvébe fel kell vennünk a modális operátorokat és egy olyan relációt, amely a lehetséges világok közti elérhetőségi kapcsolatot képezi le. A különböző modális logikákat azon az alapon különíthetjük meg egymástól, hogy feltételezzük, sokféle világ létezhet, melyek közül némelyikben igazak bizonyos állítások, másokban viszont hamisak, megint más állítások minden lehetséges világban fennállnak, míg vannak olyanok is, amelyek sehol sem igazak. Az elérhetőségi reláció azt a tényt fejezi ki, hogy adott világból szemlélve mely más világok érhetők el (aminek inverze írja le azt, hogy melyek nem). Ennek az elérhetőségi relációnak fontos szerepe van a modális logika tipizálásában. A lehetséges világok közti elérhetőségi relációra vonatkozóan különböző relációtulajdonságokat lehet megállapítani, és ezek a tulajdonságok egyben jellemzik a különböző modális logikákat is. Egy-egy ilyen relációtulajdonsággal egy-egy kalkulust definiálhatunk, amely az adott modális logika 'szükségszerű' ('erős modálisan igaz'), illetve 'lehetséges' ('gyenge modálisan igaz') fogalmára vonatkozik. A reflexivitás tulajdonságával például az ún. (T) kalkulust határozhatjuk meg, amelyre a következő formula írható fel.A (T) formulát úgy interpretálhatjuk, hogy 'ami szükségszerűen igaz, az igaz'. Első "nekifutásra" ez kijelentés magától értetődőnek tűnhet, pedig könnyen lehet olyan értelmezést találni, amikor ez az állítás nem igaz. Jobban meg lehet érteni mindezt, ha az előző mondatot átfogalmazzuk a következő alakra: 'ez így van, mert így kell lennie'. Ha a 'kell' fogalmát egy természettörvényre hivatkozva értelmezzük, akkor a "kellés" (szükségszerűség) valóban maga után vonja az állítás igazságát is: ha feldobunk egy követ, akkor annak – a tömegvonzás törvénye miatt – le kell esnie, és, valóban, a földobott kő le is esik a földre. Ha azonban a 'kellés' fogalma alatt a kötelezőséget értjük, akkor közel sem annyira magától értetődő, hogy ami kell (kötelező), annak meg is kell valósulnia, hiszen rengeteg esetet ismerünk, amikor valamilyen kötelező parancsba foglalt állítás a valóságban nem teljesült. Egy közlekedési példával szemléltetve ezt a különbséget tegyük fel, hogy éppen azt meséljük egy barátunknak, hogy egy közös ismerősünket az úttesten elütötte egy jobbról érkező autó, amire a barátunk ennyit mond:
Jobbról nem is jöhetett autó azon a helyen.
Ez a mondat kétféleképpen is értelmezhető. Nem jöhetett jobbról autó, mert (i) a gázolás egy éles kanyarban történt, és a baleset színhelyétől jobbra házfalak meredeznek, vagy (ii) egy egyenes, ám – balról jobbra – egyirányú utcában jobbról nem érkezhetett semmi a kötelező haladási iránnyal szemben. Kicsit másként: nem jöhetett jobbról az autó, mert az fizikailag lehetetlen lett volna, illetve nem jöhetett jobbról az autó, mert a tiltó jogszabály miatt nem lett volna szabad. A fenti megnyilatkozást átfogalmazhatjuk a következő formába:Nem lehetséges, hogy az adott helyen jobbról jöjjön az autó.
Ebben az esetben ugyanúgy fennáll a kettős jelentés lehetősége, csak ekkor a 'nem lehetséges' kifejezésnek adhatunk kétféle értelmezést: (i) 'nem lehetséges, mert fizikailag lehetetlen', illetve (ii) 'nem lehetséges, mert nem megengedett'. A 'lehetséges' kétféle interpretációja teljesen eltérő magyarázósémákat és különböző modális logikákat eredményez. Mielőtt bemutatnám, hogy miként is határozhatjuk meg a legfontosabb modális kalkulusokat (modális logikákat), át kell tekintenem a modális logika nyelvnek elemeit.A modális logikai nyelv elemei
Szükség van tehát egy modális logikai nyelvre, ami a következőből áll [Patri]$\mathscr{L}_{ML}$($p,q,r, A,B,C, \bot, \lnot, \lor, \Diamond)$
| $p,q,r \in \Phi$ | propozíció |
| $A,B,C$ | formula |
| $\bot$ | sosem igaz (ellentmondás) |
| $\lnot$ | tagadás logikai művelet |
| $\lor$ | diszjunkció logikai művelet |
| $\Diamond$ | lehetséges modális logikai operátor |
$A\defi p \;|\; \bot \;|\; \lnot B \;|\; B \lor C \;|\; \Diamond B$
jól-formált formula (hun) – well-formed formula (eng)
A felsorolást úgy kell értelmezni, hogy (i) jól formált formula bármely propozíció vagy az (ii) ellentmondás; (iii) ha van egy jól-formált formulánk, akkor jól-formált marad, ha tagadjuk; (iv) ha van két jól-formált formulánk, akkor ezek diszjunkciója is jól-formált; (v) ha egy jól-formált formulát összekapcsoljuk a lehetséges operátorral, akkor jól-formált formulához jutunk. Ezeket formulákat természetesen tetszőleges formában és mértékben egymásba ágyazhatjuk, így a többi ismert logikai műveletet is bevezethetjük a nyelvbe. A modális logika nyelvében két modális operátort használunk, hogy kifejezhessük velük a szükségszerűség és lehetségesség fogalmait. A két új operátor között természetesen szigorú összefüggés létezik, egyik a másikból levezethető. A különböző iskolák, szerzők különböznek abban, hogy melyik kategóriát veszik fel definiálatlan alapfogalomként (és ebből következően melyiket vezetik be a másik segítségével). Én a 'lehetséges' kategóriáját vettem fel alapként, a szükségszerű fogalmát a fent ismertetett módszer segítségével már definiálni lehet.$\concept{POSSIBLE}(A)\equiv\Diamond(A)\equiv\Diamond A $
lehetséges (hun) – gyenge modálisan igaz (hun) – gyémánt (hun) – possible (eng) – diamond (eng)
$\concept{NECESSARY}(A)\equiv\Box(A)\equiv\Box A $
szükségszerű (hun) – erős modálisan igaz (hun) – necessary (eng) – box (eng)
$\concept{(DUAL)} \defi \Box A \leftrightarrow \lnot\Diamond \lnot A$
(Dual)-séma (hun) – (Dual)-schema (eng)
A modális logika következő fontos fogalma a relációs struktúra (☜) amit azonban itt másként, keretnek neveznek. A keret segítségével léphetünk tovább következő fontos modális kategóriára, a modell fogalmára. Ez felfogható egy másodrendű relációstruktúrának, amiben egy keret és egy reláció van definiálva. A modellhez szükséges reláció egy $\rel{V}$ értékelési (valuation) függvény, amely a $A\in\Phi$ propozíciókat rendeli hozzá a $\mathbb{W}$ halmaz elemeihez. Ezt a három új fogalmat fel kell vennünk az elméletünkbe.$\concept{FRAME}\equiv \mathfrak{F}\defi(\mathbb{W},\rel{R})$
keret (hun) – frame (eng)
$\concept{VALUATION}\defi \rel{V}: \Phi \mapsto\rel{V}(A)\subseteq \mathbb{W}, p\in\Phi$
értékelés(i függvény) (hun) – valuation (function) (eng)
$\concept{MODEL}\equiv \mathfrak{M}\defi(\mathfrak{F},\rel{V})$
modell (hun) – model (eng)
A modell kategóriája azért (is) fontos, mert vele lehet az igazság vagy kielégíthetőség fogalmait értelmezni, a keret pedig az érvényesség meghatározásához szükséges. Nézzük meg előbb, hogy lehet az igazság fogalmát meghatározni. Feltételezzük, hogy $\phi,\psi$ tetszőleges formulák, $A\in\Phi$ adott propozíció, $w,u\in\mathbb{W}$ adott állapotok ($\mathbb{W}$ elemei). Ekkor az $\phi,\psi$ formulák igazságát induktív felsorolással lehet meghatározni az alábbi módon. [♦]
$\concept{SATISFIED} \equiv\;\;\models\;\; \defi$
$1)\;\;\;\;\mathfrak{M},w\models A \modefi w\in\rel{V}(A), p\in\Phi$
$2)\;\;\;\;\mathfrak{M},w\deflnot\models \bot$
$3)\;\;\;\;\mathfrak{M},w\models \lnot \phi\modefi \mathfrak{M},w\deflnot\models \phi$
$4)\;\;\;\;\mathfrak{M},w\models \phi \lor \psi \modefi \mathfrak{M},w\models \phi \deflor \mathfrak{M},w\models \psi$
$5)\;\;\;\;\mathfrak{M},w\models \Diamond \phi \modefi \;\defexists{v}\in\mathbb{W}(\rel{R}(w,v)) \defland\mathfrak{M},v\models \phi$
kielégítő (hun) – satisfied (eng) – igaz (hun) – true (eng) – szemantikai következmény (hun) – semantic consequence (eng)
A feltételeket meglepően egyszerű értelmezni. Mind az öt feltételt az adott \mathfrak{M} modellre és az adott $w$ állapotra kell értelmezni. Az első feltétel azt mondja ki, hogy az A propozícióra vonatkozóan a modell akkor (és csak akkor) elégíti ki az igazságfeltételt az adott $w$ állapotban, ha az állapot benne van a $\rel{V}$ értékelési függvény értékkészletében. A második feltétel szerint az ellentmondás nem igaz az adott modell szerint az adott $w$ állapotban. A harmadik formula azt mondja ki, hogy ha egy $\phi$ formula igaz (kielégíti az adott modellt, az adott $w$ állapotban), akkor (és csak akkor) a tagadása nem igaz. A negyedik feltétel két formula diszjunkciójára mondja ki, hogy annak igazsága a komponensformulák vagylagos igazságától függ az adott $w$ állapotban. Végül az ötödik formula rögzíti azt, hogy az adott modell szerint egy $\phi$ formula akkor lehetséges a $w$ állapotban, ha van egy másik v állapot, amely $\rel{R}$-relációban van a $w$ állapottal, és amelyben a formula igaz. Ezekkel a kielégíthetőségi feltételekkel már tetszőleges formuláról eldönthetjük, hogy igaz-e az adott modell szerint a $w$ állapotban. Azért pedig, hogy kifejezhessük azt is, ha valami nem kielégíthető, vagyis hamis, érdemes bevezetni a szemantikai következmény reláció tagadását.$\concept{FALSIFIED}\equiv\;\not{\models}\;\defi\lnot \models$
nem kielégítő (hun) – hamis (hun) – false (eng) – falsified (eng) – refuted (eng)
Ha ismerjük már a lehetséges operátor használatát, akkor nézzük meg, hogyan lehet a szükségszerű operátort alkalmazni. Az eddigiekből következik, hogy a definícióban a korábbi egzisztenciális kvantifikációt ki kell cserélni univerzálisra.$\concept{LOCALLY\_NECESSARY}\defi \mathfrak{M},w\models \Box A \modefi \;\defforall{v}\in\mathbb{W}(\rel{R}(w,v)) \defland\mathfrak{M},v\models A$
lokálisan szükségszerű (hun) – locally necessary (eng)
Ezek lokálisan érvényes kijelentések. Globálisan vagy univerzálisan igaz formula definíciója.$\concept{UNIVERSALLY\_TRUE}\defi$
univerzálisan igaz (hun) – globálisan igaz (hun) – universally true (eng) – globally true (eng)
Az értelmezést megkönnyítendő bemutatok egy példát [Patri] Vegyük a következő öt-elemű $\mathbb{W}$-halmazt, amelynek elemei közti relációt a nyilak jelzik. Az elérhetőségi reláció legyen: $\rel{R}(w_i,w_j)\leftrightarrow j=i+ 1$. Ekkor a keretünk így néz ki: $\mathfrak{F}=(\{ w_1,w_2,w_3,w_4,w_5\},\rel{R})$. Az állapotok közti kapcsolatot az alábbi grafikonnal lehet szemléltetni.
Az elérhetőségi reláció itt azt jelenti, hogy $w_1$-ből csak $w_2$, $w_2$-ből csak $w_3$, $w_3$-ból csak $w_4$ és $w_4$-ből csak $w_5$ állapot érhető el, utóbbiból pedig semmi sem. Ezen a kereten vegyük a következő értékelési függvényt: $\rel{V}(A)=\{ w_2,w_3\}, \rel{V}(B)=\{ w_1,w_2,w_3,w_4,w_5\}$, illetve $\rel{V}(C)=\emptyset$. Ekkor a $\mathfrak{M}=(\mathfrak{F}$,$\rel{R}$) modellen a következő formulák kielégítőek (igazak).
$1)\;\;\;\mathfrak{M},w_1\models \Diamond\Box A$
$2)\;\;\;\mathfrak{M},w_1\not{\models} \Diamond\Box A \to A$
$3)\;\;\;\mathfrak{M},w_2\models \Diamond (A \land \lnot C)$
$4)\;\;\;\mathfrak{M},w_1\models B \land \Diamond(B \land \Diamond(B \land \Diamond(B\land\Diamond B)))$
$5)\;\;\;\mathfrak{M}\models \Box B$
Az első formula megértéséhez elsőként meg kell állapítanunk, hogy a $\Box A$ formula igaz a $w_1$ és $w_2$ állapotban, mivel mindkettőre igaz, hogy belőlük elérhető a $w_2$, illetve $w_3$ állapot, és ezekben az A propozíció igaz. Mivel $w_1$-ból és $w_2$-ből más állapotok nem érhető el, ezért igaz az az állítás, hogy a belőlük elérhető összes állapotban fennáll az A propozíció, ez pedig $w_1$-r és $w_2$-re is $\Box A$ igazságát jelenti. Ezek után nézzük meg a $\Diamond\Box A $ formula kielégíthetőségét $w_1$-ben! Jelöljük a formulánkat így: $\Diamond(D) $. Ez akkor igaz, ha van olyan $w_1$-ből elérhető állapot, ahol a D igaz. Ilyen pedig van: mivel $w_1$-ből csak a $w_2$ állapot érhető el, és ott a $D(=\Box A)$ igaz (ahogy az előbb megállapítottuk). Az első formula tehát igaz. A második sor azt fejezi ki, hogy a $\Diamond\Box A \to A$ formula nem kielégíthető az adott modellen, a $w_1$ pontban. Ez a formula azért nem igaz, mert a kondicionális előtagja igaz (ezt az előbb néztük át), viszont a kondicionális utótagja (maga az A propozíció) nem igaz, hiszen a $\rel{V}$ értékelési függvény az A propozíciót csak a $w_2$ és $W_3$ állapotokban adja meg igaznak. Emiatt a vizsgált formulánk (kondicionálisunk) nem lehet igaz. A harmadik formula azt fejezi ki, hogy a $w_2$ állapotból elérhető egy olyan állapot (ez a $w_3$), amelyben igaz az A propozíció és nem igaz a C. Ez így is van, hiszen $w_3$-ban a $\rel{V}(A)$ igaz, a $\rel{V}(C)$ nem igaz (mivel utóbbi sehol sem igaz). A negyedik formula értelmezéséhez azt kell figyelembe vennünk, hogy az értékelési függvény szerint a B propozíció minden állapotban igaz. A vizsgált – kielégíthető – formula azt fejezi ki, hogy a $w_1$ állapotban a B propozíció igaz, és van olyan belőle elérhető állapot, amelyben a B propozíció igaz (ez a $w_2$ állapot), és van olyan állapot, amelyben a $w_2$-ből elérhető és ott a B igaz és így tovább addig, amíg az utolső állapotig el nem érünk. Az ötödik formula tartogat egy "meglepetést". A formula ugyanis azt állítja, hogy a B propozíció univerzálisan igaz, vagyis minden állapotban van egy olyan elérhető másik állapot, ahol a propozíció fennáll. Ez triviális az első négy állapotra, hiszen a belőlük elérhető szomszédos állapotokban igaz a B. Az utolsó $w_5$ állapotból azonban egyetlen más állapot sem érhető el. Erre viszont azt mondhatjuk, hogy a lokális kieléígíthetőséghez csak azt a feltételt kell kielégíteni, hogy az adott állapotból elérhető minden más állapotban igaznak kell lenni a propozíciónak. Mivel egy állapot sem érhető el a $w_5$-ből, ezért e feltétel üresen (vacuously) teljesül, és emiatt a vizsgált teljes formula igazsága is fennáll. Érdemes megnéznünk egy másik példát is [Patri] hogy még közelebb kerülhessünk az eddigi fogalmainhoz. Legyen a halmazunk $\mathbb{W}=\{1,2,3,4,6,8,12,24\}$ és az $\rel{R}(m,n)$ legyen az 'n osztható m-mel' reláció ($m\ne n$). Ekkor az 1.-ből elérhető minden más állapot, tehát {2,3,4,6,8,12,24}, a 2.-ből elérhető a {4,6,8,12,24} állapot, a 3.-ból a {6,12,24} állapot, a 4.-ből a {8,12,24} állapot, a 6.-ból a {12,24} állapot, a 8.-ból a {24} állapot, a 12.-ből a {24} állapot, és a 24.-ből nem érhető el semmi. Ezt a következő ábrával szemléltethetjük.
Legyen az értékelési függvényünk a következő: $\rel{V}(A)=\{{4,8,12,24}\}$ és $\rel{V}(B)=\{{6}\}$ (triviális értelmezésként mondhatjuk, hogy A a 4-gyel, B a 6-tal való oszthatóságot jelenti). Ekkor az adott modellünkön az alábbi formulák elégíthetők ki.
$1)\;\;\;\mathfrak{M},4\models \Box A$
$2)\;\;\;\mathfrak{M},6\models \Box A$
$3)\;\;\;\mathfrak{M},2\not{\models} \Box A$
$4)\;\;\;\mathfrak{M},2\models \Diamond(B\land \Box A)\land \Diamond(\lnot B \land \Box A)$
Nézzük meg, miért. Az 1) formula azt fejezi ki, hogy a 4. állapotból elérhető a 8., a 12. és a 24. állapot, és ezekben az értékelési függvény szerint az A formula igaz, vagyis minden olyan világállapotban, amely a 4.-ből elérhető, az A formula kielégítő. Ez pedig pont megfelel annak, hogy a $\Box A$ formula kielégíti a modellünket. A 2) sor szerint a 6. állapotból látszik a 12. és 24. állapot, és ezek mindegyikében igaz az A formula, amiből következően a 6. állapotban igaz lesz a $\Box A$ formula is. A 3) formula értelmezése: a 2. állapotból elérhető {4,6,8,12,24}, amelyek közül a 6. esetében nem teljesül az A propozíció igazsága, ezért a 2. állapotra nézve nem áll fent a $\Box A$ formula igazsága. Az utolsó formula pedig azt fejezi ki, hogy egyszerre igaz két állítás. Egyfelől a 2. állapotból elérhető legalább egy olyan világ, amelyben B is és $\Box A$ is igaz (ilyen a 6. állapot, hiszen ott a B igaz az értékelési függvény alapján, a $\Box A$ formula pedig igaz a fenti 2. formula alapján). Másfelől van legalább egy olyan állapot is, amelyben $\lnot B$ és $\Box A$ egyszerre igaz (ilyen a 4. állapot, hiszen ott B nem igaz az értékelési függvényalapjá, viszont $\Box A$ fennáll a fenti 1. formula szerint). Végül nézzünk át egy olyan példát, amit talán jobban köthetünk a mindennapi életünkhöz, mint az előző kettőt. Vegyünk pár országot: Németország (GER), Ausztria (AUT), Svájc (SUI), Olaszország (ITA), Franciaország (FRA), Magyarország (HUN), Kanada (CAN) és Egyesült Államok (USA). Nézzük meg, hogy ezekben az országokban milyen hivatalos nyelvek vannak: német (N), olasz (O), francia (F), magyar (M), angol (A). Ha az elérhetőségi reláción azt értjük, hogy két ország közt beszélnek-e közös nyelven az emberek, akkor a következő kapcsolatokat kapjuk: $\rel{R}$(HUN,$\emptyset$), $\rel{R}$(AUT,{GER, SUI}), $\rel{R}$(GBR,{USA, CAN}), $\rel{R}$(USA,{CAN, GBR}), $\rel{R}$(GER,{AUT, SUI}), $\rel{R}$(CAN,{FRA, SUI}), $\rel{R}$(ITA,{SUI}), $\rel{R}$(SUI,{GER, AUT, ITA, FRA, CAN}), $\rel{R}$(FRA,{CAN, SUI}). Tételezzük fel azt, hogy az értékelési függvényünkkel azt írjuk le, hogy a különböző országokban (világokban) hivatalos-e az adott nyelv vagy sem. Vagyis: $\rel{V}(N)=${GER, SUI, AUT} , $\rel{V}(O)=${SUI, ITA}, $\rel{V}(F)$={SUI, FRA, CAN}, $\rel{V}(M)=${HUN}. Az elérhetőségi reláció az alábbi módon kapcsolja össze a világokat.
Ebben a modellben – sok egyéb mellett – az alábbi formulák kielégíthetőek.
$1)\;\;\;\mathfrak{M},\rm HUN\models \Box M \land \Box A \land \Box N \land \Box O \land \Box F$
$2)\;\;\;\mathfrak{M}, \rm SUI\models \Box (O \lor F \lor N)$
$3)\;\;\;\mathfrak{M}, \rm USA\models \Box A$
$4)\;\;\;\mathfrak{M},\rm CAN\not{\models} \Box A$
$5)\;\;\;\mathfrak{M},\rm ITA,FRA,GER,GBR,SUI,AUT,CAN,USA \not{\models} \Diamond M$
Az 1) formula azt írja le, hogy a minden \begin{smalll}HUN-világból elérhető más világban szükségszerűen beszélik az összes nyelvet. Ez a logikai igazság azonban üres abban az értelemben. hogy csak azért igaz, mert nincs egyetlen olyan másik világ, amely elérhető lenne ebből az állapotból. Tartalmas jelentése van a 2) formulának, ez ugyanis azt takarja, hogy a Svájból elérhető világokban szükségszerűen beszélnek a német, a francia vagy az olasz nyelv valamelyikén. A 3) sorban az szerepel, hogy az Egyesült Államokból elérhető országokban szükségszerűen (mindenhol) beszélnek angolul. A 4) formula tanulsága szerint azonban ez nem igaz Kanada esetén (mivel van olyan ország, ahol az angol nem hivatalos nyelv, például Svájc). Végül az 5) sor azt a tényt reprezentálja, hogy nincs olyan ország, amelyből elérhető lenne egy olyan világ, ahol a magyart beszélik (azaz a magyar nyelv szigetként működik). A bemutatott példákból kiderül az is, hogy az $\rel{R}$ elérhetőségi relációnak tetszőleges jelentést tulajdoníthatunk. Sokféle kontextus, sokféle feltételrendszer képzelhető el, amelyeken belül más és más értelmezéseket adhatunk az elérhetőségi relációnak, és ezáltal persze másként lehet az ezekre építhető modelleket is interpretálni.
Modális sémák, kalkulusok
Ahogy korábban már láttuk, a logikai rendszerekhez axiómákat, sémákat definiálhatunk, amelyek alapján a logikai rendszer fogalmai, tételei mind levezethetőek. Ezt megtehetjük a modális logikában is, vagyis modális sémákat definiálhatunk, amelyek alapján modális kalkulusok építhethetünk fel. Egymás után definálhatunk újabb és újabb sémaaxiómákat, amelyek a korábbi axiómákkal együtt egy-egy modális kalkulust alkotnak majd – miközben mind átveszik a kijelentéskalkulus három axiómáját (☜) Az axiómasémákat pedig jellemezhetjük az elérhetőségi relációra vonatkozóan különböző tulajdonságokkal is. A következőkben sorban bemutatom a (K), a (D), a (T), a (B), az (S4) és az (S5) modális axiómasémák definícióit.$\concept{(K)} \defi \Box (A \rightarrow B) \rightarrow (\Box A \rightarrow \Box B)$
(K) (log) – disztribúciós axióma (hun) – distribution axiom (eng)
A (K)-séma jelentése annyi, hogy ha egy $A\to B$ kondicionális szükségszerűen igaz, akkor a kondicionális két tagjának szükségszerűségét is összekapcsolhatjuk a kondicionálissal. Ez tétel a modális operátorra vonatkozó disztributivitás (☜) tulajdonságát is kimondja egyben (a kondicionális műveletre nézve).$\concept{(D)} \defi \Box A \rightarrow \Diamond A$
(D) (log) – szeriális axióma (hun) – seriality axiom (eng)
A (D)-séma azt jelenti, hogy ha valami szükségszerű(en igaz), akkor az lehetséges(en igaz). Első pillantásra egy kicsit intuícióellenesnek bizonyulhat sokak számára ez a tétel, hiszen 'miért ne lenne igaz, ami szüksészerű'. Pedig ez a séma biztosítja a deontikus séma és a deontikus logika speciális minőségét. A (D)-sémában az a lényeg, ami csak implicit módon van benne: azokban a világokban, amelyek erre sémára támaszkodnak, ha valami szükségszerű (kötelező), az nem feltétlenül igaz egyben. Vagyis, ami szükségszerű (kötelező), az nem szükségszeűen teljesül, csak a lehetősége van meg ennek. Ez a séma összakapcsolható az elérhetőségi relációra vonatkozó szerialitás tulajdonságával (☜)$\concept{(T)} \defi \Box A \rightarrow A$
(T) (log) – (M) (log) – reflexivitási axióma (hun) – reflexivity axiom (eng)
Ami a (D)-sémában nem teljesül, azt mondja ki a (K)-axiómaséma: ha valami szükségszerű(en igaz), akkor az igaz. Azokra a világokra tehát, amelyeket ez a séma jellemez, teljesül az a – mint láthattuk, nem teljesen megalapozott – intuíciónk, hogy valami akkor lehet szükszerűen igaz, ha igaz is egyben. Ezt a tulajdonságot az elérhetőségi reláció reflexivitásával hozhatjuk párhuzamba (☜) Ez annyit tesz, hogy a (K)-szükségszerűség fennállása esetén nemcsak az aktuális világból elérhető más világokra vonatkozó elvárásokat az aktuális világra is ki kell terjeszteni.$\concept{(B)} \defi A \rightarrow \Box\Diamond A$
(B) (log) – szimmetricitási axióma (hun) – symmetricity axiom (eng)
A (B)-séma jelentése az, hogy ha valami igaz, akkor szükségszerű(en igaz), hogy lehetséges(en igaz). Ebben az esetben az elérhetőségi reláció szimmetrikus (☜) Első értelmezésre elfogadhatónak látszik a tétel, hiszen ha egyszer valami már fennáll, akkor ennek a lehetőségét szükségesnek érezzük, de a helyzet mégsem ilyen egyszerű. Tekintsük ugyanis a következő levezetést.
$1)\;\;\; A \rightarrow \Box\Diamond A$
$2)\;\;\; \lnot \Box\Diamond A \to \lnot A$
$3)\;\;\; \lnot(\lnot\Diamond\lnot)\Diamond A \to \lnot A$
$4)\;\;\; \Diamond\lnot\Diamond A \to \lnot A$
$5)\;\;\; \Diamond\lnot\Diamond (\lnot\lnot A) \to (\lnot A)$
$6)\;\;\;\Diamond\Box (\lnot A) \to (\lnot A)$
$7)\;\;\;\Diamond\Box B \to B$
A levezetés tanulsága az, hogy a kondicionális kontrapozíció, a kettős tagadás, a zárójelezési, a behelyettesítési és a (Dual)-szabályok segítségével a (B)-sémából levezethető a hetedik sorban látható tétel, amit már közel sem érzünk triviálisnak, sőt inkább intuícióellenesnek tartunk. A tétel ugyanis azt állítja, hogy ha valami lehet, hogy szükségszerű, akkor az igaz. Ennek az igazsága egyáltalán nem nyilvánvaló. A (B) séma elfogadása ezért mégsem annyira magától értetődő, mint az az első látásra feltételezhető lenne. Sokkal inkább elfogadható a következő axiómaséma, bár bizonyos modalitásértelmezések esetén ennek fennállását is meg lehet kérdőjelezni.
$\concept{(S4)} \defi \Box A \rightarrow \Box\Box A$
(S4) (log) – (4) (log) – tranzititási axióma (hun) – transitivity axiom (eng)
A séma azt rögzíti, hogy ha valami szükségszerű(en igaz), akkor szükségszerű(en igaz), hogy szükségszerű(en igaz). Ez az elérhetőségi reláció tranzitivitását is jelenti egyben (☜) ami abban nyilvánul meg, hogy ha valami szükségszerű egy aktuális világban, akkor nemcsak belőle elérhető szomszédos világokban, de az azokból elérhető "másodszomszédos" világokban is szükségszerű lesz. Az erre a sémára épülő S4-kalkulusban interpretáljuk úgy – Gödel nyomán – a $\Box A$ formulát, hogy annak az 'A bizonyított állítás' jelentést tulajdonítjuk. Ezzel az értelmezéssel az S4 kalkulus a bizonyítottság [♦] (vagy bizonyíthatóság) logikájának tekinthető [Ruzsa]$\concept{(S5)} \defi \Diamond A \rightarrow \Box\Diamond A$
(S5) (log) – (E) (log) – euklideszi axióma (hun) – euclidean axiom (eng)
A legerősebb S5-kalkulus alapsémája az (S5), amelynek jelentése: ha valami lehetséges(en igaz), akkor szükségszerű(en igaz), hogy lehetséges(en igaz). Ez az értelmezés a sémát az elérhetőségi reláció euklideszi tulajdonságával kapcsolja össze (☜) Ebben a kalkulusban adhatjuk azt az értelemzést a $\Box A$ formulának, hogy 'analitikusan igaz, hogy A'. Ha így teszünk, akkor a kalkulussal az analicitás, vagyis az analitikus állítások logikáját kapjuk [Ruzsa] Vigyázni kell azonban ezzel az értelmezéssel, mert nem jelent minden esetben egyértelmű segítséget akkor, amikor el akarjuk dönteni egy állításról, hogy analitikus-e vagy sem. [♦] Fontosnak tartom újra hangsúlyozni, hogy a fenti definíciók csak egy-egy axiómasémát határoznak meg, és csak úgy jutunk kalkulusokhoz a segítségükkel, ha az "alattuk levő" többi axiómát is beemeljük az adott kalkulusba (vagy ha nem is mindet, de legalábbis a legtöbbet). És az axiómák mellé szükség van még levezetési szabályokra is. Egyfelől minden modális kalkulus átveszi a modus ponens szabályt (☜) illetve a behelyettesíthetőségre is kimondanak egy szabályt, de ezzel itt nem foglalkozom. A modális kalkulusokhoz azonban kell még egy további levezetési szabály is, amit többféleképpen is neveznek, de persze a definíció minden esetben ugyanaz.$\concept{(NEC)}\;\defi\; \vdash A \;\Rightarrow\; \vdash \Box A$
szükségességi szabály (hun) – modális generalizálás szabálya (hun) – Necessitation Rule (eng) – Modal Generalization rule (eng) – (Nec) – (log) – (Gen) – (log)
Ez a levezetési szabály tehát olyan, mint a modus ponens, ami szükséges az axiómákból és tételekből való következtetések levonásához. Az értelmezése egyszerű: ha egy A formula(osztály) eleme egy logikai nyelvnek, akkor a $\Box A$ formula is eleme lesz. A fent bemutatott sémát (és kalkulusok) közül a továbbiakban a (D) séma és a hozzá tartozó modális logika a deontikus logikában (☜) és a doxasztikus logikában (☜) lesz különösen fontos, a (K), (T), (B), (S4) és (S5) sémákat pedig az episztemikus (☜) és a preferencialogikában (☜) fogjuk majd alkalmazni. A modális logikai fejezet lezárásaként ki kell mégtérnem a modális logika és a logikai négyszög kapcsolatára. Utóbbit ugyanis alkalmazhatjuk a modális logikai operátorokra is. Sőt, a modális operátorokra nemcsak a négyszögbe, de a hatszögbe rendezés is értelmes. Ha a legáltalánosabb modális logikai hatszöget akarjuk felrajzolni, akkor a szükségszerűség és lehetségesség terminusai helyett az erős és gyenge modális operátorokat használva felrajzolhatunk egy újabb logikai hatszöget bemutató ábrát.
Hasonló ábrát lehetne felrajzolni az alethikus logikára, ami a szükségszerűség és a hozzá kapcsolódó fogalmak összefüggéseit mutatná, és a többi modális logika esetében is ugyanúgy érvényesnek bizonyulna a logikai hatszög az operátorok közti összefüggések vizuális szemléltetésére [Bziau] [Jean-] [Aless]
Episztemikus és doxasztikus logika
Az episztemikus logika, illetve a doxasztikus logika a modális logikának az az ága, amely a vélekedés, tudás, ismeret, hit logikai leírásának lehetőségeivel foglalkozik. Azonnal képet kaphatunk, mire lehet jó ez a diszciplina, ha felidézünk egy arab közmondást. Ez az ősrégi bölcselet olyasvalamit állít az ember és tudás viszonyáról, ami – időben sokkal később – bekerült az episztemikus logikai diskurzusba is. Így szól.
"Négyféle ember van.
Aki nem tudja, és nem tudja, hogy nem tudja: a balga – kerüld őt;
Aki nem tudja, de tudja, hogy nem tudja: az egyszerű – tanítsd őt;
Aki tudja, de nem tudja, hogy tudja: alszik még – ébreszd fel őt;
Aki tudja, és tudja, hogy tudja: ő a bölcs – őt kövesd."
[Reaso]
Episztemikus logika
Az episztemikus logikát úgy építhetjük fel, hog először átértelmezzük a modális logika (K)-kalkulusát, majd azt további axiómákkal bővítve egyre erősebb nyelvhez jutunk [Reaso] Induljunk ki tehát a (K)-kalkulus nyelvéből.$\mathscr{L}_{EL}$($\mathscr{L}_{(K)C}, \modop{K})$
| $\mathscr{L}_{(K)C}$ | (K)-kalkulus |
| $\modop{K}_i$ | tudja |
$\concept{TUDJA} \equiv \modop{K}_i(\phi) \equiv \modop{K}_i\phi \;\defi \forall i(\Box_i \phi), i\in\mathbb{N}^{+}$
tudja (hun) – tudja, hogy (hun) – knows (eng) – knows that (eng)
A modális logika (K)-kalkulusát (☜) itt úgy vehetjük át, hogy a szükségszerűség operátort a fentiek szerint átértelmezzük. A különböző szerzők többféle alakban is kifejezik az axiómát, amelyek természetesen teljesen ekvivalensek egymással. Kettőt bemutatok közülük: elsőként a modális (K)-kalkulus alakhű átértelmezését, majd utána egy átalakított formulát [Reaso] Az episztemikus disztribúciós szabályt tehát – kétféle formában – a következőképpen rögzíthetjük.$\concept{(K')}\defi \modop{K}_i(\phi \to \psi) \to (\modop{K}_i\psi \land \modop{K}_i\psi)$ $\concept{(K'')}\defi (\modop{K}_i\phi \land \modop{K}_i(\phi \to \psi)) \to \modop{K}_i\psi$
episztemikus disztribúciós axióma (hun) – epistemic distribution axiom (eng)
A disztibúciós axiómát úgy is interpretálhatjuk, hogy a tudás zárt a logikai következményre (implikációra), azaz ha valaki tuda, hogy $\psi$ állítás a $\phi$-nek következménye, és még azt is tudja, hogy $\phi$ fennáll, akkor tudnia kell azt is, hogy a következmény, vagyis $\psi$-nak is fenn kell állnia. Természetesen az episztemikus kalkulushoz is következtetési szabály(oka)t kell rendelnünk. Itt is érvényesnek tarthatjuk a modus ponens szabályt (☜) a modális generalizálás szabályát (☜) pedig át kell értelmezzük a \modop{K} tudásoperátorra vonatkozóan.$\concept{(MP)} \defi \{A, (A \to B)\} \Rightarrow B$
modus ponens következtetési szabály (hun) – modus ponens inference rule (eng)
$\concept{(NEC)}\defi\;\vdash \phi \;\Rightarrow\; \vdash \modop{K}_i \phi$
tudásgeneralizáció szabálya (hun) – (Nec) (log) – (Gen) (log) – Knowledge Generalization rule (eng)
Növelni lehet az episztemikus logika erősségét, ha további modális sémákat veszünk fel a kalkulusba. Első lépésként felvehetjük a modális (T)-sémát (☜) az axiómák közé (természetesen episztemikus módon interpretálva). Ennek az lesz az eredménye, hogy a tudás fogalma összekapcsolódik az igazságéval. További hozadéka lesz még a (T)-séma alkalmazásának az a tény, hogy ennek segítségével meg tudjuk különböztetni a tudás és a vélekedés fogalmát egymástól, amikor pont a (T)-axiómához való eltérő viszonyulás alapján definiáljuk a vélekedés fogalmát, s ezzel magát a doxasztikus logikát (☜) A modális (T)-séma episztemikus átértelmezése eredményeként az alábbi formulához jutunk.$\concept{(T)} \defi \modop{K}_i \phi \rightarrow \phi$
tudás axióma (hun) – knowledge axiom (eng) – igazság axióma (hun) – truth axiom (eng) – episztemikus (T)-séma (hun) – epistemic (T)-schema (eng)
Nagyon fontos minőséget jelent ez tétel a tudás fogalmának értelmezésekor. Ha azt mondjuk, hogy tudunk valamit, akkor annak igaznak kell lennie. Nagyon erős állítás ez – különösen a vélekedés, hit definíciójával szembeállítva. Tovább bővítjük az episztemikus kalkulust, ha felvesszük az axiómák közé a \modop{K} tudás-operátorra vonatkozó (S4) modális sémát (☜) Ennek a lépésnek az lehet az értelme, hogy ezáltal az ágens saját tudásának tudásáról, vagyis introspekcióról, egyfajta reflektáltságról beszélhetünk. A formulában természetesen ebben az esetben is ki kell cserélnünk a modális operátorok szimbólumait.$\concept{(S4-PIK)} \defi \modop{K}_i \phi \to \modop{K}_i \modop{K}_i \phi$
pozitív introspekciós axióma (hun) – positive introspection axiom (eng) – (S4) (log) – (KK) (log) – reflektált pozitív tudás (hun) – reflected positive knowledge (eng)
Az axiómát úgy interpretálhatjuk, hogy ha az i ágens tud valamit, akkor tudja azt is, hogy tudja azt a valamit. Ez abban az értelemben erős tudás, hogy reflektált. A fejezetet elején mottóként közölt versrészlet szereplői közül az – utolsóként megénekelt – bölcsre illik ez a jellemzés. Az ősi versben dramaturgiai szerepe van, ahogy követik egymást az egyre inkább reflektált tudással bíró szereplők, így lehet eljutni a teljesen (reflektálatlanul) tudatlan embertől a reflektáltan tudó bölcsig. Az episztemikus logika másként "működik". Ha az episztemikus kalkulusba felvesszük az (S5) modális sémát is (☜) akkor olyan tudásoperátorhoz (tudástípushoz) jutunk, amit a köznapi gondolkodás még nem sokra tart. Ennek az új episztemikus sémának a jelentését és értelmét csak akkor érthetjük meg igazán, ha átalakítjuk az (S5)-sémát az $A=\lnot \phi$ egyenlőség, illetve a (Dual)-séma (☜) alapján.
$1)\;\;\;\Diamond A \rightarrow \Box\Diamond A$
$2)\;\;\; \lnot \Box \lnot A \rightarrow \Box\lnot\Box \lnot A$
$3)\;\;\; \lnot \Box \phi \rightarrow \Box\lnot\Box \phi$
$\concept{(S5-NIK)} \defi \lnot \modop{K}_i \phi \to \modop{K}_i \lnot\modop{K}_i \phi $
negatív introspekciós axióma (hun) – negative introspection axiom (eng) – (S5) (log) – reflektált negatív tudás (hun) – reflected negative knowledge (eng)
Az axióma értelmezése az lehet, hogy ha az i ágens nem tud valamit, akkor tudja, hogy nem tudja. Logikai szempontból ez az – átalakított (S5)-sémával kiegészített – kalkulus a legerősebb. Eszerint az igazi bölcs az, aki egyaránt tudja azt, hogy mit tud, és azt is, hogy mit nem. Definiálhatunk még további levezetési szabályokat is, például a monotonitás vagy a kongruencia szabályait. Ezeket azért mondhatjuk levezetési szabályoknak, mert a nyelv zártságát definiálják a kongruencia és monotonitás tulajdonságaira nézve.$\concept{(MON)}\defi \;\vdash (\phi\to \psi)\Rightarrow \;\vdash (\modop{K}_i \phi \to \modop{K}_i \psi)$
monotonitási szabály (hun) – monotony rule (eng) – (Mon) (log)
$\concept{(CGR)}\defi \;\vdash (\phi\leftrightarrow \psi)\Rightarrow\;\vdash (\modop{K}_i \phi \leftrightarrow \modop{K}_i \psi)$
kongruencia szabály (hun) – congruence rule (eng) – (Cgr) (log)
Ezeket a szabályokat úgy is értelmezhetjük, hogy ezek azt fejezik ki, hogy a tudással rendelkező ágensek képesek tudássá formálni a logikai állításokat, vagyis ha egy adott episztemikus modellben érvényes egy kondicionális vagy egy bikondicionális művelet, akkor az összetevőkre vonatkozó tudások köztött is fennáll ugyanaz a művelet. Lehetne még további szabályokat definálni, amelyek mind az ágensek logikai következtető képességét fejeznék ki más és más logikai műveletekre fókuszálva, de ezt a képességet kifejezhetjük egy még általánosabb formában is. Rögzíthetünk ugyanis egy nagyon erős, és ezért sokak által vitatott következtetési szabályt is, ami azt írja le, hogy ha a logika szabályai szerint egy adott formális elméletből (mondhatjuk így is: formulák valamilyen konjunkciójából) levezethető egy tétel, akkor az elmélet minden formulája (vagyis a konjunkciók elemi komponensei és a konjunkcióból következő "új" formula egyaránt) ismert az adott ágens számára. Formálisan kifejezve ezt a következő képletet kapjuk.$\concept{(RK)}\defi \;\vdash (\phi_1 \land \phi_2 \land \dots \land \phi_n \to \psi)\Rightarrow \;\vdash (\modop{K}_i \phi_1 \land \modop{K}_i \phi_2 \land \dots \land \modop{K}_i \phi_n \to \modop{K}_i \psi), n\in\mathbb{N}$
logikai mindentudás szabálya (hun) – knowledge logical omniscience rule (eng) – (RK) (log)
Akik ezt a szabályt "bevezették", érvényesnek tartották, azt abból a megfontolásból tették, hogy ennek segítségével lehet az episztemikus képességekkel rendelkező ágensek viselkedését minél jobban lemodelezni, számítógépes szimulációját minél jobban megvalósítani. Tették ezt abban a – jogos – meggyőződésben, hogy az ágenseik mindig megbízhatóan képesek a logikai szabályok figyelembe vételével helyes következtetéseket levonni. Ez a számítógépes modellezés során teljesen elfogadható. Akik viszont ezt a szabályt támadják, azok arra hivatkoznak, hogy az emberek esetében sokszor nem teljesen megalapozott ez az elvárás, az emberek nem képesek minden és mindenfajta logikai feladatot megoldani. A fenti szabályra valóban rá lehet húzni a "logikai mindentudás" kifejezést, de az ember esetében ennek teljes körű érvényeségét nem szabad feltételeznünk. Ez nyilván nem logikai és – bizonyos értelemben – nem elméleti probléma. Egy cselekvéselmélet építése során azonban mégiscsak figyelembe kell venni az ember korlátait, ezért úgy gondolom, hogy ezt a szabályt erős fenntartásokkal kell kezelnünk. Nem eldobni kell, csak mindvégig figyelni kell az emberek valóságos logikai következtető képességeinek tényleges korlátaira. Nézzük meg a következő példát!Laci tudja, hogy Kati nem tudja, hogy Béla nem hiszi, hogy Klára tudja, hogy Péter azt hiszi, hogy a németek mind tudják, hogy az amerikaiak hisznek abban, hogy A.
Egy ilyen állítást tényleges tartalmát már nem igazán vagyunk képesek befogadni, noha az egymásba ágyazott elemi állítások mindegyike könnyen értelmezhető. A hétköznapi gyakorlatban azonban sosem fordulnak elő ilyen hosszúságú (és összetettségű) mondatok, ezért nem tudjuk értelmezni. Egy számítógép számára viszont – persze csak akkor, ha az általa olvasható formában áll rendelkezésre – ugyanolyan könnyedén feldolgozható ez a mondat is, mint azok az egyszerűek, amelyeket még mi is kezelni tudunk. A fenti példamondat a közösségi helyzeteket jellemzi, amikor nem az összetett mondat bonyolultsága jelenti a nehézséget, hanem az egy csoportba tartozó, tudással rendelkező ágensek egyéni tudásainak egymásra vonatkozása. A másikfajta feldolgozási nehézséget az összetett mondatok logikai szerkezetének bonyolultsága okozhatja. A jogi nyelvben könnyedén találhatunk olyan sokszorosan egymásba ágyazott, összetett mondatokat, amelyek értelmezése a laikus embereknek mindenképpen, de akár még a jogászok számára gondot okozhatnak. Az episztemikus logika fent jelzett feltételezése, hogy az ágensek teljesen racionálisak abban az értelemben, hogy tökéletes következtetési képességgel rendelkeznek – mind minőségi, mind mennyiségi értelemben, elvileg elfogadható. Gyakorlati szempontból viszont ez a feltételezés túlságosan erős, és a tényleges társadalmi gyakorlat tényleges ágenseire csak korlátozott mértékben szabad vonatkoztatni.Doxasztikus logika
A (T)-séma azért lehet alkalmas a tudás és vélekedés fogalmainak elválasztására, mert amíg a tudás fogalmával szemben fenntarthattuk a séma érvényességét (☜) addig a vélekedésre vonatkozóan pont az ellenkezőjét kell mondanunk: ebben az esetben érvénytelennek kell tartanunk az igazság axiómát. Azt ugyanis mondhatjuk, hogy valaki igaznak vél valamit, ami hamis, de ilyenkor hozzá kell tennünk, hogy tévesen véli, tévesen hiszi azt, ami nem igaz. Azt viszont nem mondhatjuk, hogy valaki tud valamit, ami hamis. Ha valami hamis, akkor az nem tudás, csak – hamis – vélekedés. [♦] Ezen a ponton lehet elágaztatni az episztemikus és doxasztikus logikát egymástól azon az alapon, hogy amíg az előbbi a tudás, addig az utóbbi a vélekedés fogalmának formalizálásával foglalkozik. Mielőtt belekezdenék a doxasztikus logika vagyis a vélekedés (hit) logikájának bemutatásába, jeleznem kell, hogy ezt a logikát annyira közelállónak lehet tekinteni az episztemikus logikához, hogy nem érdemes számára új nyelvet definiálni. Ezért az itteni tételeket ugyanúgy az episztemikus logikára utaló 'EL' szimbólummal azonosítom, a tételek számozását folytatom. A doxasztikus logika központi kategóriája a vélekedés, amit a tudás fogalmával szemben kell értelmeznünk. Ha a tudásra érvényesnek, a vélekedésre érvénytelennek tartjuk a (T) tudás axiómát, akkor kérdés, hogy milyen tulajdonsággal jellemezhetjük a vélekedés fogalmát. Ehhez a modális logika (D)-sémáját kell elővenni, amit persze újfajta módon kell értelmeznünk. Ahhoz, hogy megértsük, mi lehet az megfelelő új interpretáció, át kell alakítani kicsit a modális logika (D)-sémáját.
$1)\;\;\;\concept{(D)}\equiv \Box \phi \to \Diamond \phi$
$2) \;\;\; \Box \phi \to \lnot\Box\lnot\phi$
$3)\;\;\;\modop{B}_i\phi\to\lnot\modop{B}_i\lnot\phi$
Az 1) és 2) között kicseréltük a $\Diamond$ lehetséges operátort a (Dual)-szabály alapján a $\Box$ szükségszerű operátorra (külső és belső tagadással együtt), majd a 2) és 3) között a modális szükségszerű operátort a $\modop{B}_i$ vélekedésoperátorral helyettesítettük. Ezek alapján a következő formulával határozhatjuk meg a vélekedés egy nagyon fontos tulajdonságát.
$\concept{(D-CB)} \defi \modop{B}_i \phi \to \lnot\modop{B}_i \lnot \phi $
konzisztencia axiómája (hun) – Consistency of Belief axiom (eng) – doxasztikus (D)-séma (hun) – doxastic (D)-schema (eng)
Ez a formula a vélekedés (hit) konzisztenciájáról szól, ugyanis azt rögzíti, hogy ha valaki hisz valamiben ($\phi$-ben), akkor nem hihet annak az ellenkezőjében ($\lnot\phi$-ben). Ez a tudásra nem lenne igaz, csak a vélekedésre. Ezért ez a (T)-axiómánál gyengébb episztemikus (D)-séma a vélekedést, a hitet jellemző doxasztikus logika specifikumát adja. A vélekedéshez a \modop{B} szimólumot és a következő axiómát rendelhetjük.$\concept{BELIEF} \defi \lnot\modop{B}_i \bot$
vélekedés (hun) – belief (eng)
A formulát úgy értelmezhetük, hogy valaki (az i ágens) nem hiheti azt, hogy egy ellentmondás igaz lehet (nagyon fontos nem "elfelejteni", hogy ebben az esetben az episztemikus (T)-sémát nem tartjuk érvényesnek). A (T)-séma érvénytelensége miatt a doxasztikus logika nem olyan erős, mint az episztemikus logika (T)-sémával megerősített változata. A doxasztikus logikában is értelmezhetjük az (S4) és (S5) axiómákat tartalmilag a tudás kapcsán bemutatott interpretációhoz hasonlóan.$\concept{(S4-PIB)} \defi \modop{B}_i \phi \to \modop{K}_i \modop{B}_i \phi$
a hit pozitív introspekciós axiómája (hun) – positive introspection of belief (eng) – doxastic (S4) (log) – (BB) (log)
$\concept{(S5-NIB)} \defi \lnot \modop{B}_i \phi \to \modop{K}_i \lnot\modop{B}_i \phi $
a hit negatív introspekciós axiómája (hun) – negative introspection of belief (eng) – doxastic (S5) (log)
A tudás és vélekedés viszonyára vonatkozóan kimondható egy fontos axióma (amiről azért tudni érdemes, hogy vannak, akik vitatják az érvényességét).$\concept{KB}\defi\modop{K}_i \phi \to \modop{B}_i \phi$
a hit tudás alapú axióma (hun) – knowledge imply belief axiom (eng)
A doxasztikus logikában is felvehető a (RK)-szabály "megfelelője", annyit kell csak tennünk, hogy a tudásoperátort kicseréljük a vélekedésoperátorra.$\concept{(RB)}\defi \;\vdash (\phi_1 \land \phi_2 \land \dots \land \phi_n \to \psi)\Rightarrow \;\vdash (\modop{B}_i \phi_1 \land \modop{B}_i \phi_2 \land \dots \land \modop{B}_i \phi_n \to \modop{B}_i \psi), n\in\mathbb{N}$
a logikai mindenhit szabálya (hun) – belief logical omniscience rule (eng) – (RB) (log)
Kollektív tudás
Sok szó esett már eddig a tudás, a hit fogalmáról, és bár mindvégig nyilvánvaló volt, hogy az ezeket reprezentáló operátorokat ($\modop{K}_i$, illetve $\modop{B}_i$) össze kell kapcsolnunk azokkal az ágensekkel, akit "hordozzák" a tudás- és hittartalmakat, viszont eddig csak jeleztük ezt a kapcsolatot, de nem igazán használtuk ki ezt az információt. A társadalmi cselekvések és társadalmi kapcsolatok értelmezése során rendkívüli jelentősége van annak a ténynek, hogy a tudás, a hit lényege szerint kollektív jelenség, az ágensek a saját egyéni tudásaikat kicserélhetik, megoszthatják egymás között, az egyéni tudásaikat mások tudásaira "vonatkoztathatják", és ezáltal az egyéni tudások mellett másfajta, kollektív tudások is megjelennek a társadalmi térben. A kollektív tudás jelenségének fontosságát önmagában jelzi az a tény, milyen sokféle terminust használunk ebben a fogalomkörben. A későbbiekben a közös tudás, a közismert tudás, illetve a elosztott tudás fogalmait fogom majd a társadalmi cselekvés modelljébe beemelni, de ezekkel együtt fordulnak elő a terepen az olyan kategóriák, mint az együttes tudás, kölcsönös tudás, köztudott tudás, magától értetődő tudás, nyilvános tudás, kumulatív tudás, kollektív bölcsesség, szétszórt tudás, csoporttudás. Mindezeket pedig együttesen lefedi a kollektív tudás felettes fogalma. A három kiemelten kezelni kívánt fogalom közül igazából csak a közös tudás és az elosztott tudás fogalma a fontos, a közismert tudás kategóriájára csak azért van szükségünk, hogy a közös tudás jelenségét értelmezni tudjuk a segítségével. A következőkben ezért előbb a közös tudás fogalmát mutatom be, majd ezt követi az elosztott tudás fogalmának rövid ismertetése. A közös tudás jelenségét először David Lewis vizsgálta monografikus igényességgel a 'Convention' című könyvében [david] majd még sokan követték őt a jelenség értelmezésében. A jelenség megragadására John McCarthy, a mesterséges intelligencia egyik úttörő kutatója javasolta használatba venni a "minden bolond tudja" ("any fool knows") kifejezést [Reaso] de ez – számomra – inkább a közismert tudás jelentését sugallja. Nehéz ezekkel a kifejezésekkel pontosan operálni. Nem is tehetünk mást, mint hogy egy-egy kifejezést kiragadunk a szokásos diskurzusból, és pontos, rögzített jelentéssel látjuk el őket. Ezáltal persze elszakadunk attól a lehetőségtől is, hogy a hétköznapi gyakorlatból eredő intuícióinkra hivatkozzunk. Ahhoz, hogy a kollektív tudás és más hasonló fogalmak elemzésébe kezdjünk, először be kell vezetnünk a társadalmi {csoport} fogalmát. A csoportba tartozó ágensek tudásait, hiteit vizsgálva, a csoport egyes tagjait indexekkel jelölve, a csoport fogalmára hivatkozva definiálhatjuk majd a kollektív tudás általános kategóriája alá sorolható további tudásfogalmakat. A tudást hordozó ágens, az ágenseket összefogó csoport fogalmával itt még nagyon kell foglalkoznunk, ezekre a fogalmakra később még úgyis kitérek még. Most elég csak rögzíteni, hogy vannak ágensek, akik csoportokba rendeződ(het)nek. A csoportot G-vel jelöljük, az ágenseket, ha ez nem zavaró, akkor az i természetes számokkal azonosítjuk, ha szükséges, akkor az $a_i$ szimbólumot alkalmazzuk rájuk. A közösség ekkor a tagjainak uniója. [♦]
$G \defi \bigcup \limits_{i=1}^{n} a_i$
csoport (hun) – group (eng) – közösség (hun)
Az i. ágenshez kapcsolható $\modop{K}_i$ egyéni tudás operátorát már sokat használtuk korábban, most kell kidolgoznunk azokat a tudásfogalmakat, amelyek segítségével már meg tudjuk ragadni az egyéni tudások kölcsönösségét, egymásra vonatkozatottságát, illetve le tudjuk írni a csoport egészéhez köthető tudásokat is. Ehhez azonban először meg kell tudnunk adni azt, hogy az ágensek egyénileg milyen tudásokkal rendelkeznek. Ehhez nem kell mást tennünk, mint összegezni az egyes egyénekre az elemi tudásaikat. Ekkor is használhatjuk a már bevezetett $\modop{K}_i$ tudásoperátort, és ha csak magában használjuk, akkor az i. egyén össze tudását érttjük alatta, ha pedig a tudásoperátor után teszünk még az adott tudáselemre utaló jelet, akkor értelemszerűen az arra a konkrét tudáselemre vonatkozó tudás tényét állítjuk. Most tehát az egyén teljes tudását kell definiálnunk.
$\modop{K}_i \defi \bigcup \limits_{j=1}^{m} \modop{K}_i \phi_j$
egyén teljes tudása (hun) – agent's full knowledge (eng)
Az egyén teljes tudása (tudattartalma) az egyéni tudáselemek uniója. [♦] Ez a fogalom segíteni fog minket a kollektív tudás körébe tartozó fogalmak értelmezésében. Lássuk, hogyan! A közös tudás fogalmának értelmezéséhez először a közismert tudás kategóriáját kell bevezetnünk, ami nem egy bonyolult fogalom. Azt a jelenséget ragadhatjuk meg vele, amikor egy csoporton belül egyénileg mindenki rendelkezik ugyanazzal a $\phi$ tudással, vagyis amit "minden bolond tud". Ha a G csoport bármelyik i tagja tudja $\phi$-t, akkor azt a következő formulával írhatjuk le.
$\modop{K}^E_G \phi \defi \bigcap \limits _{i \in G} \modop{K}_i \phi $
közismert tudás (hun) – köztudott tudás (hun) – együttes tudás (hun) – magától értetődő tudás (hun) – közös tudás (hun) – mutual knowledge (eng)
Nehéz széles körben elfogadott, a fenti formulával definiált, pontos jelentés mentén értelmezett kifejezést rendelni ehhez a fogalomhoz. A definíció alatt felsorolt nyelvi alakzatok mindegyike használható lenne, csak a választási kényszer miatt emeltem ki közülük egyet (a 'közismert tudás' kifejezést), de ha nem lesz zavaró, a későbbiekben is megengedhetőnek tartom, hogy szinonímaként használjuk az alternatív kifejezéseket a fogalomra vonatkozóan. [♦] A közismert tudás definíciója a G csoport egészére, de egyetlen $\phi$ tudáselemre vonatkozik. Továbbléphetünk egyet, ha erre a fogalomra támaszkodva definiáljuk a csoport teljes közismert tudását.
$\modop{K}_G^E \defi \bigcap \limits_{i=1}^{n} \bigcup \limits_{j=1}^{m} \modop{K}_i \phi_j$
(csoport teljes) közismert tudás(a) (hun) – group's full mutual knowledge (eng)
A $\modop{K}^E_G$ közismert tudáskészlet minden $\modop{K}_i$ egyéni tudáskészletben benne van, vagyis a $\modop{K}^E_i$ egyéni tudatok össztartalma mindig szélesebb vagy azonos terjedelmű, mint a $\modop{K}^E_G$ közismert tudat. Lehetséges (bár nem valószínű), hogy a $\modop{K}^E_G$ közismert tudat megegyezik valamelyik i személy $\modop{K}_i$ egyéni tudattartalmával. Amennyiben nem ez a helyzet áll fent (és ez a valószínűbb kimenet), akkor azt mondhatjuk, hogy $\modop{K}^E_G$ közismert tudat különbözik minden egyes $\modop{K}_i$ egyéni tudattól. Ilyen esetben hiába van jelen a $\modop{K}^E_G$ kollektív tudat minden eleme az összes $\modop{K}_i$ egyéni tudatban, mégis különbözik mindegyiktől, vagyis a kollektív tudat mindegyik egyéni tudathoz képest más. Ez a fontos meglátás az alapja Emilé Durkheim társadalomelméletének is. A tudást közismertnek mondhatjuk abban az értelemben, hogy mindenki részesül belőle. Azonban ez nem jelenti azt, hogy annak is tudatában lennének a csoport tagjai, hogy ezt a valamennyiük által egyénileg birtokolt tudást valamennyien ismerik. Sőt, elvileg az is elképzelhető, hogy mindenki azt feltételezi, hogy csak ő rendelkezik az adott tudással, senki más. Andersen meséje a meztelen királyról szép példája annak, hogy ami közismert tudás egy közösségen belül, az még nem feltétlen jelent közös tudást is egyben. Mindenki látta, tudta, hogy a királyon nincs ruha, de amíg valaki el nem kiáltotta magát, hogy "a király meztelen", addig senki sem tudhatta, hogy amit egyénileg mind tudnak, azt mindenki más is tudja, vagyis a tudás közös. Az Andersen-mesének persze létezik más olvasata is, de ez a tény nem teszi érvénytelenné a rá való hivatkozást ezen a ponton. Ha azt akarjuk megragadni, ami az Andersen-mese tanulsága, akkor a közös tudás (vagy kölcsönös tudás) fogalmát kell definiálnunk. Ehhez új elemként fel kell vennünk a nyelvünkbe a közös tudást reprezentáló $\modop{K}^C_G$ modális operátort, amit a következőképpen definiálhatunk. Ehhez a $\modop{K}_i$ egyéni tudások alapján képezhető közismert tudásoknak az egymásra vonatkozó – iterációval kifejezhető – közös metszetét kell előállítanunk, amihez egy segédformulát kell igénybe vennünk. Utóbbival azt a közismert tudást kell kifejeznünk, hogy valamelyik (j) csoporttag tudja, hogy a másik csoporttag ($j- 1$) tudja, hogy $\phi$. A közös tudás fogalmát ez alapján úgy ragadhatjuk meg, hogy egy "végtelen" iterációba állítjuk ezt a segédfogalmat.$\modop{K}^{E,j}_G \phi \defi \modop{K}^{E}_G\modop{K}^{E,j - 1}_G \phi $
(j. csoporttag) iterált tudása (hun) – iterated knowledge of $j^{th}$ group member (eng)
$\modop{K}^C_G \defi \bigcap \limits_{j=1}^{\infty}\modop{K}^{E,j}_G \phi $
(csoport teljes) közös tudás(a) (hun) – kölcsönös tudás (hun) – common knowledge (eng) – mutual knowledge (eng)
A fogalom értelmezése: a G csoport minden tagja tudja, hogy a másik tudja, és tudja, hogy a másik tudja, hogy ő tudja, és így tovább. Elméletileg egy végtelen processzussal tudjuk kifejezni a közös tudás fogalmát (nem is kevesen vannak, akik épp ezért nem fogadják el sem a fenti definíciót, sem az effajta értelmezési irányt). Fentebb említettem, hogy Andersen 'A császár új ruhája' című meséjéhez többféle értelmezést is hozzárendelhetünk. Legalább három lehetőség adódik. Azért interpretálhatunk többféleképpen is, mert van egy nagy adag bizonytalanság abban, hogy miként lehet előállítani azt a helyzetet, ami a közös tudáshoz eléréséhez szükséges "tudom, hogy tudja" állapotot eredményezi. Az első lehetőség az, hogy valóban nem tudják a csoporttagok, hogy a többiek tudják, amit maguk egyénileg mind tudnak, és a nyilvános bejelentés mindenkit meglep. Ilyen esetekben az a bejelentés, aminek eredményeként a közös tudás létrejön, csodálkozást, meghökkentést, meglepetést vált ki a csoport tagjaiban. A második értelmezés szerint a csoporttagok mind sejthetik, de nem tudhatják biztosan, hogy a többiek is a közös tudás birtokában vannak. Ekkor a mindenki által tudott tudás közzététele a korábbi bizonytalanságból adódó feszültség feloldódásához, egyfajta megkönnyebbüléshez, megnyugváshoz vezet. A harmadik értelmezési lehetőséget nem lehet teljes mértékben elválasztani a második interpretációtól, de érdemes elkülöníteni tőle. Előfordulhat ugyanis, hogy az egyetemesen birtokolt egyéni tudások azért nem válhatnak sokáig közös tudássá, mert a közzététel útjában társadalmi akadályok vannak, valamiért nem lehet kimondani a közösség előtt a mindenki által tudott tudást. Ez is feszültséget okozhat a csoport tagjaiban, ám az ilyen helyzetekhez másfajta érzelmek kapcsolódnak, és ha mégis megszületik a nyilvános bejelentés, akkor azt felszabadultság követi (az Andersen-mesében ez utóbbival állunk szemben, amit a tömeg reakciója bizonyít: a királyt leleplező felkiáltás után a tömeg nevetésben robban ki). A közös tudás fogalmának tárgyalásakor az volt a fontos, hogy mi az a tudáselem, amit a közösség tagjai mind közösen birtokolnak, vagyis hogy mi az, ami ott van a csoport mindegyik tagjának a fejében. Az elosztott tudás fogalmával nem az ebben az értelemben vett közös részt akarjuk megragadni, hanem valami mást. A kollektív bölcsesség elve, a 'sok kicsi sokra megy' mondása és még sok minden más ősrégi megfigyelés fejezte és fejezi ki azt a társadalmi tényt, hogy a közösség olykor több lehet, mint a részei, vagyis a tagjai összessége. Azt a tudásösszességet, ami a közösség egésze rendelkezésére áll nevezhetjük elosztott tudásnak. A korábban bevezetett egyéni teljes tudás fogalmára támaszkodva már könnyen definiálhatjuk ezt a fogalmat.$\modop{K}^D_G \defi \bigcup \limits_{i=1}^{n} \bigcup \limits_{j=1}^{m} \modop{K}_i \phi_j$
csoport teljes elosztott tudása (hun) – group's full distributed knowledge (eng)
Ez a tudásfogalom nem más, mint az egyéni tudattartalmak (tudáselemek) uniója, vagyis a csoport tagjainak fejében levő tudás valahogyan képzett összessége. Francis Galton 1907-ben publikált egy cikket a Nature-ben egy Plymout városában tartott állatvásár tapasztalatairól [Galto] A látogatókat versenyre invitálták: meg kellett becsülni egy levágandó bika vágás utáni súlyát. A versenynek jelentkezési díja volt, ami miatt gyakorlatilag ki lehetett zárni a "vicces becsléseket", viszont komolynak mondható díjat ajánlottak fel a nyertes számára, ami miatt sokan beszálltak a játékba. A verseny után a közel nyolcszáz játékos által leadott papírokat Galton megkapta, és elemezte a rajtuk található adatokat. Meglepő eredmény született: az 1198 font súlyú állatra leadott becslések mediánja 1207 font lett, ami az egy százalékos hibahatáron belül maradt. Galton a "kísérlet" eredményét a demokratikus szavazás, a Vox Populi elvének igazolásának is szánta, bár ebben nem volt teljesen igaza (mivel itt tényre vonatkozó átlagolásról, a demokratikus szavazás során értékre vonatkozó átlagolásról van szó).Dinamikus logika
A dinamikus logikát (dynamic logic) eredetileg a számítógépes programok leírására hozták létre, hogy legyen olyan eszköz, amelynek segítségével meg lehet vitatni a programok helyességét, de a nyelv idővel egészen másfajta alkalmazási területeken is hasznosnak bizonyult. A dinamikus logika a modális logika egyik típusa. Központi kategóriája a program(darab) fogalma, ami értelmezhető úgy is, hogy valamely cselekvést (action) kell végrehajtania. A program(darab)ot a-val jelöljük. Két deontikus operátort használunk a szükségszerű és lehetséges operátorok helyett:| $\Box p$ | helyett: | $[a]p$ |
| $\Diamond p$ | helyett: | $\langle a \rangle p$ |
$\mathscr{L}_{DL}([], \langle\rangle, 1, 0, \cup, \cap, ;, \ast, ?)$
| $[a]p$ | ha megteszed $a$-t, kötelező, hogy $p$ | |
| $\langle a \rangle p$ | ha megteszed $a$ t, lehetséges, hogy $p$ | |
| 1 | SKIP/NOP | ne csinálj semmit, állj le a programmal (terminálj) |
| 0 | BLOCK, konstans | ne csinálj semmit |
| $a \cup b$ | egyesítés | tedd meg a-t vagy b-t |
| $a;b$ | komponálás | tedd meg a-t, utána b-t |
| $a\ast$ | iterálás | ismételten tedd meg (véges sokszor) a-t |
| $a \cap b$ | egyszerre futtatás | tedd meg a-t és b-t |
| $a?$ | tesztelés | ha a igaz, akkor tedd meg, ha hamis, akkor állj le |
| $[a]p \equiv \neg \langle a \rangle \neg p$ | operátorok közti transzformáció |
| $(\vdash p \land \vdash p \rightarrow q)\rightarrow \vdash q$ | modus ponens |
| $\vdash p \rightarrow \vdash [a]p$ | szükségességi szabály (necessitation rule) |
$[0]p$
$[1]p \equiv p$
$[a \cup b]p \equiv [a]p \land [b]p$
$[a;b]p \equiv [a][b]p$
$[a \ast]p \equiv p \land [a][a\ast]p$
$p \land [a \ast](p \rightarrow [a]p) \rightarrow [a\ast]p$
$[x:=e]\Phi (x)=\Phi(e) $
$[p?]q \equiv p \rightarrow q$
Az általános axiómák és a műveletekre vonatkozó axiómák alapján levezethetőek azok az egyenlőségek is, amelyek a másik dinamikus logikai operátorra állapítanak meg összefüggéseket:
$\neg \langle 0 \rangle p$
$\langle 1\rangle p \equiv p$
$\langle a \cup b\rangle p \equiv \langle a\rangle p \lor \langle b\rangle p$
$\langle a;b\rangle p \equiv \langle a\rangle \langle b\rangle p$
$\langle a $\ast$\rangle p \equiv p \lor \langle a\rangle \langle a $\ast$\rangle p$
$\langle a $\ast$\rangle p \rightarrow p \lor \langle a $\ast$ \rangle (\neg p \land \langle a \rangle p)$
$\langle p?\rangle q \equiv p\land q$
Nem tartozik a könyv témájához, de ha már itt vagyunk, érdemes megjegyezni, hogy a programozás két fontos konstrukciója, az 'if-then elágazás' és a 'while-ciklus' is egyszerűen definiálható a dinamikus logika operátoraival.
$\concept{IF} \;p\; \concept{THEN} \;a\; \concept{ELSE} \;b\; \defi (p?;a)\cup (\neg p?;b)$
$\concept{WHILE} \;p\; \concept{DO} \;a\; \defi (p?;a)\ast; \neg p?$
Logikából nagyon sokféle van. A mérnökök, informatikusok ezerfélét kidolgoztak a legkülönfélébb célokra, a legkülönbfélébb szintaxissal, a legkülönfélébb képességekkel. A dinamikus logika csak egy a sok közül, ami csak azért kell számunkra, mert a társadalmi cselekvés szempontjából fontos fogalmak közül többet is dinamikus logikai alapon formalizáltak.
Preferencialogika
Ha azt mondjuk, hogy A-t preferáljuk B-vel szemben, akkor nem teszünk mást, mint valamiféle sorrendet alakítunk ki a két dolog között. A sorrendállítás pedig rendezést jelent. Rendezésből persze többféle van, erről bővebben írtam a könyv relációelméleti részében (☜) A matematikai rendezésfogalmak azonban túl általánosak, ezért sok jelenségre "ráhúzhatók". Ha speciálisabb rendezési fogalmakat szeretnénk definiálni, szükségünk lehet további tulajdonságokat kikötni. A reflexív, antiszimmetrikus és tranzitív tulajdonságok egyidejű feltételezésével többféle rendezési relációt is jellemezhetünk. A része (partitív), a tartalmazási, a nem öregebb vagy a kisebb vagy egyenlő reláció esetén egyaránt fennállnak a jelzett tulajdonságok, és érezzük, hogy szükség lenne további minőségeket hozzájuk rendelni, hogy jól elkülöníthessük őket egymástól. A partitív reláció esetében megtette ezt Peter Simon vagy Archello Varzi. Előbbi könyvet írt a rész fogalmáról [simon] utóbbi axiómarendszert dolgozott ki a partitív reláció fogalmára [Varzi] amelyben a három alaptulajdonságon túl még 4-5 további tulajdonságot definiált. [♦]
$\forall x (\rel{P}(x,x))$
$\forall x \forall y (\rel{P}(x,y)\land \rel{P}(y,x)\to x=y)$
$\forall x \forall y \forall z (\rel{P}(x,y)\land \rel{P}(y,z)\to \rel{P}(x,z))$
Az első három axióma rögzíti, hogy a $\rel{P}$ partitív reláció reflexív (a$_1$), antiszimmetrikus (a$_2$) és tranzitív (a$_3$). A következő lépésben a $\rel{P}$ relációval néhány új mereológiai relációt definiálunk, majd az újakkal még újabbakat hozunk létre:
$\rel{PP}(x,y)\defi \forall x\forall y (\rel{P}(x,y)\land \lnot \rel{P}(y,x))$
$\rel{O}(x,y)\defi \forall x\forall y \exists z(\rel{P}(z,x)\land \rel{P}(z,y))$
$\rel{U}(x,y)\defi \forall x\forall y \exists z(\rel{P}(x,z)\land \rel{P}(y,z))$
$\rel{OX}(x,y)\defi \forall x\forall y (\rel{O}(x,y)\land \lnot \rel{P}(x,y))$
$\rel{UX}(x,y)\defi \forall x\forall y (\rel{U}(x,y)\land \lnot \rel{P}(x,y))$
$\rel{PO}(x,y)\defi \forall x\forall y (\rel{OX}(x,y)\land \rel{OX}(y,x))$
$\rel{PU}(x,y)\defi \forall x\forall y (\rel{UX}(x,y)\land \rel{UX}(y,x))$
Sorba definiáljuk a következő relációkat: valódi része (1), átfedése (2), kívüllevősége (3), részhatáros átfedése (4), részhatáros kívüllevősége (5), valódi lefedése (6), valódi kívüllevősége (7). Ezekután a $\rel{P}$ része, $\rel{O}$ átfedése és $\rel{U}$ kívüllevősége relációk segítségével először meghatározhatjuk a kiterjeszthetőség (erős) elvét (a$_4$), majd az (a$_5$)-(a$_7$) mereológiai axiómák elfogadásával definiálhatjuk a zárt (extenzionális) mereológia elméletét.
$\forall x\forall y (\lnot \rel{P}(x,y) \exists z(\rel{P}(z,x)\land \lnot \rel{O}(z,y)))$
$\forall x\forall y (\rel{U}(x,y)\to \exists z\forall w(\rel{O}(w,z)\leftrightarrow (\rel{O}(w,x)\lor O(w,y))))$
$\forall x\forall y (\rel{O}(x,y)\to \exists z\forall w(\rel{P}(w,z)\leftrightarrow \rel{P}(w,x)\land P(w,y))))$
$\forall x\forall y \exists z ((\rel{P}(z,x)\land \lnot \rel{O}(z,y))\to \exists z\forall w(\rel{P}(w,z)\leftrightarrow (\rel{P}(w,x)\land \lnot \rel{O}(w,y))))$
További axiómák felvételével egyrészt definiálhatjuk az általános (extenzionális) mereológia elméletét (a$_8$) másrészt meghatározhatjuk az atomos (a$_9$), illetve atom nélküli mereológiákat (a$_{10}$).
$\exists x \phi \to \exists z\forall y(\rel{O}(y,z)\leftrightarrow (\exists x(\phi\land \rel{O}(y,x))$
$\forall x\exists y(\rel{P}(y,x)\land \lnot \exists z \rel{PP}(z,y))$
$\forall x\exists y(\rel{PP}(y,x))$
A mereológia elméletének bemutatásához, megérttetéséhez nyilván nem elégséges, hogy formulákkal definiáljuk az alaprelációkat, meg az axiómákat, és kész. Én mégis ezt tettem meg itt. Azért csak ennyit foglalkoztam a kérdéssel, mert csak azt akartam megmutatni, hogy a része reláció meghatározásához milyen logikai apparátust kell megmozgatni. Nem elég rögzíteni az első három relációtulajdonság meglétét, mert azzal csak egy "szimpla" rendezési relációt határozhatunk meg, ami túl általános, még nagyon sokféle dolgot képes lefedni. Láthattuk, hogy további 5-6 axióma kell ahhoz, hogy a partitív reláció specifikumát megtaláljuk. Ez az egész pedig csak azért érdekes e könyv mondanivalója szempontjából, mert a preferenciarelációra is ki lehet jelenteni, hogy az aszimmetrikus és tranzitív egyben, ám ezzel még biztos nem tudjuk megragadni a preferenciareláció különlegességét, hiszen több más ismert relációt jellemezhetnek ezek a minőségek, ezért keresni kell még további tulajdonságokat hozzá. Ezt végzik el azok a szerzők, akik a preferencialogika különböző elméleteit dolgozzák ki. Georg Henrik Von Wright is, a követői is szokták a preferencia terminusa helyett a – magyarra lefordíthatatlan – betterness terminust használni. A kategória tartalmát talán a meglehetősen kicsavart jobbnak tartottság kifejezéssel adhatnánk vissza, de e jelzésen túl, hogy létezik, ezt a terminust a természetes nyelvi szövegben inkább nem használom. [♦] Hansson szerint amikor másokról beszélünk, akkor inkább a "preferálja" terminust használjuk, és amikor magunkra utalunk vagy imperszonális módon nyilatkozunk, akkor inkább a "jobb" terminust alkalmazzuk [SvenO] A preferenciarendezés valamilyen halmaz elemeinek kívánatosság szerinti sorbarendezését jelenti. A preferenciarendezés reláció. Mint minden relációnak, úgy a preferenciarendezésnek is vannak argumentumai, relátumai. A preferencia jelenségéről beszélve könnyen átválthatunk, átváltunk reifikált tárgyalásmódba. Amikor a 'preferencia' terminust használjuk (például feltesszük a kérdést: "Neked mi a preferenciád?"), akkor észrevétlenül a preferenciarendezés eredményére irányul a figyelmünk. Ilyenkor a preferenciarelációt tárgyiasítjuk. A preferenciarendezés fogalma az összehasonlítandó alternatívák viszonyát vonatkozik, nem az összehasonlítás eredményére. Ez a beállítódás arra hasonlít, amikor a "vágy" terminusát használjuk. A vágyunk tárgya egy preferenciareláció reifikátuma. Amikor a vágyunkra gondolunk, már nem a valamivel való összehasonlításra, hanem csak a rendezés eredménye jár a fejünkben. Az angol nyelvben ritkán használt, de létező terminus a 'preferent', magyarban nincs megfelelője, ezért a preferált alternatíva kifejezést használjuk a preferenciarendezés előnyben részesített relátumára vonatkozóan. A preferenciarendezést el kell választani a preferenciális választástól (preferential choice) is. A választásainkban valamilyen módon mindig megnyilvánulnak a preferenciáink, de nem minden preferenciánk jelent választást is egyben. Von Wright két példát is ad erre vonatkozóan. Az egyik példa szerint preferálhatjuk ugyan a különféle időjárás jelenségek közül (napos idő, viharos idő, kánikula stb.) egyiket a másikkal szemben, de nem választhatunk belőlük. Ugyanez igaz az egészségi állapotunkra is. Hiába tartjuk jobbnak az egészséget a betegségnél, nem áll módunkban választani ezen állapotok közül (legfeljebb csak áttételesen, az életmódválasztásokon keresztül). A preferencia fogalmilag feltételezi a diszkrimináció létezését: ha m alternatívát preferáljuk n-vel szemben, akkor ezennel n-t diszkrimináljuk egyben. A diszkrimináció (vagy a diszkriminálás) a preferencia (vagy a preferálás) konverze. Természetesen a tárgyiasítás a másik irányban is működhet, vagyis a reifikálás a rendezési reláció másik relátumára a diszkriminált alternatívára is vonatkozhat. Ezzel azonban kevesebbet foglalkoznak a szakirodalomban. Amikor a hasznosság (utility) fogalmát elemzik a közgazdászok, akkor olykor felbukkan az a nézet, hogy a hasznosság dipólusos fogalom, tehát a szokásos, pozitív értelméhez képest létezik a másik véglete is: ez a negatív hasznosság, kellemetlenség, károsság (disutility), de ez ritkán történik meg. Pedig a döntéseink során figyelünk mindkét pólusra: a munkába álláskor a munkás hasznosságának számít a munkabére, a kellemetlensége pedig a munkavégzés okozta fáradtság, kimerülés. A preferenciarelációt, a szemantikailag ide kapcsolható további relációkat, valamint az ezek közti összefüggéseket a preferencialogika (BL) segítségével lehet definálni. Mielőtt bemutatnám, hogyan tehetjük meg ezt, előtte még el kell választani a preferenciák két típusát. Ez a megkülönböztetés azért nagyon fontos, mert ez alapján lehet majd a döntéseinkben, választásainkban tetten érhető kétféle értékválasztási, preferenciarendezési mód, helyzet között különbséget tenni. Elsőként az intrinzikus preferencia fogalmát elemzem, majd másodjára térek rá az extrinzikus preferenciák tárgyalására.
Intrinzikus preferencia
Von Wright saját esszéjében nem használta ki, de a társadalmi cselekvés modellezése során komoly jelentősége lesz annak a megkülönböztetésnek, amelynek segítségével von Wright definiálta a intrinzikus (intrinsic), illetve a extrinzikus (extrinsic) preferencia fogalmát." … egy személy például preferálhatja a bordói vörös bort a rajnai fehérrel szemben azért, mert az orvosa azt ajánlotta neki, vagy azért, mert sajátmaga kitapasztalta, hogy az első bor jobbat tesz a gyomrának vagy általában az egészségének. Ebben az esetben az 'ez jobb, mint az' ítélet alapjául vagy indokául szolgál a preferenciának. Azt a preferenciát nevezem extrinzikusnak. … Előfordulhat azonban az is, hogy ez a személy nem azért preferálja a bordói bort a rajnaival szemben, mert azt gondolja, hogy az jobbat tesz neki, hanem pusztán csak azért, mert az elsőt jobban szereti. Ilyenkor az egyik bor szeretete nem indoka, értelme a preferenciájának." [vonwr]
Ez utóbbit nevezi von Wright intrinzikus preferencának. Mondhatnám, hogy ez a megkülönböztetés azért fontos, mert von Wright a preferenciákról szóló esszéjében csak az intrinzikus preferenciákkal foglalkozik. De nyilván nem véletlenül. Von Wright azt akarja megfogni, hogy mi a lényege azoknak a kedveléseknek, preferenciakinyilatkozásoknak, amelyek a legbensőnkből jönnek, amelyek a legkevésbé és a leglassabban változnak, amelyek kinyilvánításakor nem mérlegelünk, "nem gondolkozunk", amelyek az értékelköteleződéseink legmélyebb rétegét jelentik. Egy későbbi tanulmányában így ír erről."Az x és y közötti preferencia extrinzikus, ha létezik egy olyan (nem cirkuláris) érv, amely megadja, $x$-t miért preferáltuk $y$-nal szemben. Minden más esetben a preferencia intrinzikus. Azt, hogy $x$ intrinzikusan preferált $y$-nal szemben, úgy is kifejezhetjük, hogy azt mondjuk, $x$ 'önmagában' vagy 'önmagáért' preferált $y$-nal szemben. Az intrinzikus preferencia kinyilvánítása, a legtöbb esetben, kifejezi azt, amit szeretünk." [G.H.v]
Ezzel a megkülönböztetéssel persze sok esetben nagyon nehéz mit kezdeni. Az, hogy mikor számít valami extrinzikus vagy intrinzikus preferenciának, mikor jön valami belülről, mikor támaszkodunk külső észérvekre, sok esetben nagyon nehezen dönthető el, ha eldönthető egyáltalán. De egyelőre nem a nehézségekkel kell foglalkozni, hanem a jelenségek jobb megértésével, amihez nyilván hasznos eszköz az ideáltípusokra támaszkodó megközelítés alkalmazása. Igazából minden preferenciát négy-argumentumú relációként kellene kifejeznünk. Az összehasonlítandó alternatívák mellett ugyanis mindig meg kellene adnunk, hogy az adott preferencia kinek az értékítéletét fejezi és mikor. Hiszen, tudjuk jól, ugyanazon dolgokra vonatkozó preferenciarendezés más lehet attól függően, hogy kiknek a preferenciájáról van szó, illetve egy személy preferenciája is változhat az időben. Ennek ellenére a preferenciával foglalkozó elméletek nem veszik figyelembe az ágencia és az idő dimenzióit. Leginkább azért nem, mert a preferencia jelenségének megértéséhez érdemben nem (vagy csak keveset) ad hozzá e két szempont figyelembe vétele. Ezért a továbbiakban személytelenített és időtlenített (imperszonális és atemporális) módon fogom én is elemezni a preferencia fogalmát. A teljeskörű leírást biztosító mondat a következő lenne.$A$ preferálja $m$-t $n$-nel szemben $t$ időpontban
Ebből az állításból azonban – elhagyva a személyi és időbeli vonatkozásokat – csak annyit hagyunk meg a továbbiakban, hogy:valaki preferálja $m$-t $n$-nel szemben
Ez a megoldás egyszerűbbé teszi a jelenség tárgyalását. Von Wright is erre hivatkozva fogadta el ezt a szűkítést. Ezen túl azonban tett még egy olyan további leegyszerűsítést is, amit a preferenciával foglalkozó későbbi kutatók már nem fogadtak el. Von Wright ugyanis nemcsak az extrinzikus preferenciákra zárta ki a tárgyalásból, de lemondott az intrinzikus preferenciák változásainak vizsgálatáról is."Csak azokat a preferenciákat tanulmányozzuk, amelyek egy személy intrinzikus preferenciái egy adott pillanatban. Ezzel a tárgyalásból kizárjuk mind a preferenciákat támogató érveket, mind a preferenciák változásának lehetőségét." [vonwr]
A fenti szűkítések miatt von Wright preferencialogikája statikus maradt, mivel nem tudta leírni a preferenciák változásait. Sem a mérlegelés nélküli, "belülről jövő" preferenciák változásait, sem a preferenciák mérlegelés, befolyásolás hatására bekövetkező, "külsődleges" változásait. A von wright-i preferencialogikát ezért ki kell egészítenünk az extrinzikus preferenciákat leíró logikával, illetve bővítenünk kell olyan módon, hogy dinamikus preferencialogikához jussunk. Ezt azonban csak később végezzük el. Előtte definálnunk kell egy nyelvet, ami az intrinzikus preferenciák leírására alkalmas lehet.$\mathscr{L}_{BL}(\mathscr{L}_{QL}, \concept{PREF}, \rel{P})$
| $\mathscr{L}_{QL}$ | predikátumlogika |
| $\rel{P}$ | preferenciareláció |
Az intrinzikus preferencia tulajdonságai
Von Wright abból indult ki, hogy bár a preferenciarelációt sok minden "dolog" között alkalmazhatjuk, elég csak a világállapotok közti preferenciarelációt vizsgálni, mert minden más eset visszavezethető erre. [♦] Ezután megadott öt axiómát, amivel definiálni lehet a preferencia fogalmát. Von Wright első lépésben két relációalgebrai tulajdonság (az aszimetrikusság és a tranzitivitás) tételezésével a preferenciarelációt a szigorú rendezési reláció egyik típusának minősítette. Ezután pedig megállapított három további ekvivalenciát, amelyek segítségével transzformációs (konjunkciós, disztribúciós, amplifikációs) műveletek végezhetők el. Az öt kritérium formulája a következő.$\concept{STRICT\_PREFERENCE}(m,n)\equiv\rel{P}(m,n)\equiv\rel{P}\equiv\rel{R}^{>}\equiv m > n\equiv \;>$
szigorú preferenciarendezés (hun) – erős preferenciarendezés (hun) – preferenciarendezés (hun) – preferencia (hun) – strict preference (eng) – strong preference (eng)
$\concept{ASYMMETRIC}(\rel{P}(m,n))\defi \forall m\forall n(\rel{P}(m,n)\to\lnot\rel{P}(n,m))$
aszimmetrikus (hun) – asymmetric (eng)
$\concept{TRANSITIVE}(\rel{P}(m,n))\defi \forall m\forall n \forall o(\rel{P}(m,n) \land \rel{P}(n,o) \to \rel{P}(m,o))$
tranzitív (hun) – transitive (eng)
$\forall m\forall n (\rel{P}(m,n)\leftrightarrow\rel{P}(m \land\lnot n, \lnot m \land n))$
konjunktív expanzió elve (hun) – principle of conjuctive expansion (eng)
$\forall m\forall n \forall o \forall p(\rel{P}(m\lor n,o\lor p)\leftrightarrow(\rel{P}(m\land\lnot o \land\lnot p,\lnot m \land\lnot n \land o)\land$
$\rel{P}(m \land\lnot o \land\lnot p,\lnot m\land\lnot n\land p) \land$
$\rel{P}(n \land\lnot o\land\lnot p,\lnot m \land\lnot n \land o)\land$
$\rel{P}(n \land\lnot o \land\lnot p,\lnot m \land\lnot n \land p)))$
disztribúció elve (hun) – principle of distribution (eng)
$\forall m\forall n \forall o(\rel{P}(m,n)\leftrightarrow(\rel{P}(m \land o,n \land o)\land \rel{P}(m \land\lnot o,n \land\lnot o)))$
amplifikáció elve (hun) – principle of amplification (eng)
A preferenciareláció fenti tulajdonságaira támaszkodva von Wright további két fontos diadikus preferenciarelációt határozott meg, ami azonban – tágabb kontextusba helyezve a dolgokat – három relációval hozható kapcsolatba. Az egyik az indifferencia reláció, amit von Wright azzal a minőséggel definál, hogy két állapot egyike sem preferált a másikkal szemben [vonwr] Ezen a ponton vigyázni kell, mert könnyen zavart okozhat az a tény, hogy ugyanezt a relációt más szerzők egészen más szemantikával értelmezik, és hol összehasonlíthatatlansági relációnak [HAndr] hol 'ugyanolyan, mint' relációnak nevezik [Roder] Von Wright is tisztában van azzal, hogy kétfajta relációról van szó, ezért a most tárgyalt relációnak kicsit később a gyenge indifferencia nevet adja [vonwr] A későbbi félreértések elkerülése végett von Wright névadási javaslatát csak a jelzős szerkezetben viszem tovább. Mindez persze csak terminológiai kérdés, jelentését tekintve az új relációt egyféleképpen vezethetjük be a formális modellünkbe.$\concept{INCOMPARABILITY}(m,n)\equiv\rel{R}^\#(m,n)\equiv\rel{R}^\#\equiv\rel{J}(m,n)\equiv\rel{J}\defi \forall m \forall n(\lnot\rel{P}(m,n)\land \lnot\rel{P}(n,m))$
összehasonlíthatatlanság (hun) – gyenge közömbösség (hun) – gyenge indifferencia (hun) – incomparability (eng) – weak indifference (eng) – ugyanolyan értékes, mint (hun) – same value as (eng)
A közömbösségi reláció terminusra vonatkozóan pedig, amit von Wright az erős indifferenciának nevezett el, meghagyom a sokkal inkább elterjedt – jelző nélküli – indifferencia vagy közömbösség megnevezést. Ebben az esetben tagadás nélkül állítjuk az egyidejűleg két irányú preferálás tényét.$\concept{INDIFFERENCE}(m,n)\equiv\rel{I}(m,n)\equiv\rel{I}\equiv\rel{R}^{\equiv}\equiv\;\shortparallel(m,n)\equiv m\shortparallel n\equiv\;\shortparallel\defi \forall m \forall n(\rel{P}(m,n)\land \rel{P}(n,m))$
indifferencia (hun) – erős indifferencia (hun) – erős közömbösség (hun) – strong indifference (eng) – indifference (eng) – értékegyenlőség (hun) – value equality (eng) – ugyanolyan, mint (hun) – ugyanolyan jó, mint (hun) – equally good as (eng) – same as (eng)
Utóbbi relációra vonatkozóan von Wright bevezetett még egy újabb megnevezést is, és értékegyenlőség relációnak nevezte el, de ezt a terminust nem fogom használni, csak a történeti érdekesség miatt említem meg. Von Wright a közömbösségi relációt nem a fent megadott képlet alapján definiálta, hanem négy ugyanolyan axiómákat rögzített, mint amilyeneket a preferenciareláció bevezetésekor kötött ki, és egy újat adott meg.$\concept{SYMMETRIC}(\rel{I}(m,n))\defi \forall m \forall n(\rel{I}(m,n)\to\rel{I}(n,m))$
szimmetrikus (hun) – asymmetric (eng)
$\concept{TRANSITIVE}(\rel{I}(m,n))\defi \forall m \forall n \forall o (\rel{I}(m,n)\land\rel{I}(n,o)\to\rel{I}(m,o))$
tranzitív (hun) – transitive (eng)
$\forall m \forall n(\rel{I}(m,n)\leftrightarrow\rel{I}(m \land\lnot n,\lnot m\land n))$
konjunktív expanzió elve (hun) – principle of conjuctive expansion (eng)
$\forall m \forall n \forall o \forall p(\rel{I}(m \lor n,o \lor p)\leftrightarrow\rel{I}(m \land\lnot o \land\lnot p,\lnot m \land\lnot n \land o)\land$
$\rel{I}(m \land\lnot o \land\lnot p,\lnot m \land\lnot n \land p)\land$
$\rel{I}(n \land\lnot o \land\lnot p,\lnot m \land\lnot n\land o)\land$
$\rel{I}(n \land\lnot o \land\lnot p,\lnot m \land\lnot n \land p))$
disztribúció elve (hun) – principle of distribution (eng)
$\forall m \forall n \forall o(\rel{I}(m,n)\leftrightarrow\rel{I}(m \land o,n \land o)\land\rel{I}(m \land\lnot o,n \land\lnot o))$
amplifikáció elve (hun) – principle of amplification (eng)
A fenti formulák együttes igazsága – von Wright intuíciója szerint – szükséges és elégséges feltétel az értékegyenlőségi reláció meghatározásához. A preferenciareláció axiómáival összevetve látható, hogy az ötből tétel közül csak az elsőben különbözik a két reláció: a preferencia aszimmetrikus, az értékegyenlőség szimmetrikus. Ez azt is jelenti egyben, hogy a von Wright értelmezésben vett preferenciareláció és értékegyenlőség reláció segítségével előállíthatunk egy olyan preferenciarendezési fogalmat is, amelyben a preferencia fogalma nem a 'szigorú értelemben vett jobb', hanem a 'legalább olyan jó' jelentés mellett értelmezhető.$\concept{WEAK\_PREFERENCE}(m,n)\equiv\rel{R}(m,n)\equiv\rel{R}\equiv\rel{R}^{\geq}(m,n)\equiv\rel{R}^{\geq}\equiv m\ge n\equiv \;\ge\defi \forall m \forall n(\rel{P}(m,n)\lor\rel{I}(m,n))$
gyenge preferencia (hun) – preferencia (hun) – legalább olyan jó, mint (hun) – jobb vagy ugyanolyan (hun) – weak preference (eng) – preference (eng)
A legalább olyan jó értelmezésű $\rel{R}$ gyenge preferenciarelációra ugyanazokat a tulajdonságokat rá lehet vetíteni, mint amiket a szigorú preferenciarendezés, illetve közömbösségi relációval szemben von Wright kikötött. A három preferenciarelációt, a szigorú és gyenge preferenciarendezést, valamint a közömbösségi relációt (és olykor még az összehasonlíthatatlansági relációt is) együttesen ($\rel{P}$, $\rel{I}$, $\rel{J}$) preferenciastruktúrának is szokták nevezni, és bizonyos tételeket a struktúra egészére vonatkozóan szoktak kimondani [M.Rou] A preferenciareláció eddigi axiómái alapján von Wright már meghatározhatónak gondolta két fontos monadikus (vagy unáris) preferenciareláció, a jó (good) és a rossz (bad) fogalmát is. Mivel von Wright a preferenciát a világállapotokra vonatkoztatva definiálta, ezért ebben az elméletben a jó és rossz kategóriája is (világ)állapotokra vonatkozóan érvényes. Szerinte a jó (állapot) így tehát az az állapot, amely feltétel nélkül preferált saját ellentétével szemben, míg a rossz (állapot) az, amelynek az ellentéte feltétel nélkül preferált magával szemben. [♦] A meghatározások megfelelő formulái [vonwr]
$\concept{GOOD}(m)\equiv\rel{G}^{'}(m)\equiv\rel{G}^{'}\defi\rel{P}(m,\lnot m)$
$\concept{BAD}(m)\equiv\rel{B}^{'}(m)\equiv\rel{B}^{'}\defi\rel{P}(\lnot m, m)$
$\concept{CONTRA-TRANSITIVE}(\rel{P}(m,n))\defi\forall m \forall n \forall o((\lnot\rel{P}(m,n) \land \lnot\rel{P}(n,o))\to\lnot\rel{P}(m,o))$
negatívan tranzitív (hun) – negatively transitive (eng) – contra-transitive (eng)
Ezután definiáltak még további három axiómát, de mielőtt bemutatnám ezeket, előtte érdemesebbnek tűnik felsorolni azt, hogy milyen további monadikus és diadikus preferenciarelációkat vezettek még be Chisholmék az első két axiómájukra támaszkodva. Azért érdemes előbb megismerni ezeket, mert az ismeretükben könnyebb lesz majd értelmezni a további axiómákat. Lássuk tehát az öt új Chisholm-Sosa-féle preferenciarelációt. [♦]$\concept{SAME\_VALUE\_AS}(\rel{S}(m,n))\equiv\rel{S}(m,n)\defi\forall m \forall n (\lnot\rel{P}(m,n) \land \lnot\rel{P}(n,m))$
ugyanolyan (hun) – ugyanolyan értékes, mint (hun) – same value as (eng)
$\concept{INDIFFERENT}(\rel{I}^{''}(m))\equiv\rel{I}^{''}(m)\defi\forall m (\lnot\rel{P}(m,\lnot m) \land \lnot\rel{P}(\lnot m,m))$
indifferens (hun) – közömbös (hun) – indifferent (eng)
$\concept{NEUTRAL}(\rel{N}^{''}(m))\equiv\rel{N}^{''}(m)\defi\forall m \exists n (\rel{I}(m) \land \rel{S}(m,n))$
neutrális (hun) – semleges (hun) – neutral (eng)
$\concept{GOOD}(\rel{G}^{''}(m))\equiv\rel{G}^{''}(m)\defi\forall m \exists n (\rel{I}(m) \land \rel{P}(m,n))$
jó (hun) – good (eng)
$\concept{BAD}(\rel{B}^{''}(m))\equiv\rel{B}^{''}(m)\defi\forall m \exists n (\rel{I}(m) \land \rel{P}(n,m))$
rossz (hun) – bad (eng)
A továbblépés előtt érdemes itt pár megjegyzést tenni. Az ugyanolyan, mint reláció megegyezik a korábban bemutatott von wrighti gyenge indifferencia relációval (☜) A fenti öt relációból csak az első diadikus, a többi monadikus, vagyis csak mindegyiknek egy argumentuma van. Arra is figyelni kell nagyon, hogy amíg Chisholm és Sosa itt mindegyikhez egy-egy pontos és egyértelmű jelentés rendel, addig a köznyelv ezeket a terminusokat sokféle értelemben használja. Az $\rel{S}(m,n)$ ugyanolyan és az $\rel{I}(m)$ indifferens reláció csak abban különbözik egymástól, hogy az első két-, a második egyargumentumú. Két állapot (alternatíva) ugyanolyan, ha egyik sem jobb, mint a másik, egy állapot pedig önmagában indifferens, ha nem jobb a tagadásánál, és a tagadása sem jobb az állapotnál. Az $\rel{S}(m,n)$ és az $\rel{I}(m)$ segítségével lehet definiálni a neutrális állapotot. E fogalom alatt Chisholm és Sosa egy olyan m indifferens állapotot értenek ($\rel{I}(m)$), amely legalább egy másik n állapothoz képest ugyanolyan értékű ($\rel{S}(m,n)$). Hasonló logika mentén a $\rel{G}(m)$ jó az az $\rel{I}(m)$ indifferens állapot, amely legalább egy másik állapothoz képest jobb ($\rel{P}(m,n)$), a $\rel{B}(m)$ rossz állapot pedig az az $\rel{I}(m)$ indifferens állapot, amelyhez képest legalább egy másik állapot jobb ($\rel{P}(n,m)$). [♦] Ezek alapján könnyebben meg lehet majd érteni, milyen minőségeket akartak Chisholmék az alábbi három axiómájukkal megragadni.$\forall m \forall n((\lnot\rel{P}(m,\lnot m)\land\lnot\rel{P}(\lnot m,m)\land \lnot\rel{P}(n,\lnot n)\land\lnot\rel{P}(\lnot n,n))\to(\lnot\rel{P}(m,n)\land\lnot\rel{P}(n,m)))$
Chisholm-Sosa első axiómája (hun) – first axiom of Chisholm-Sosa (eng)
$\forall m\forall n((\lnot\rel{P}(n, \lnot n) \land \lnot \rel{P}(\lnot n,n)\to\rel{P}(m,n))\to\rel{P}(m,\lnot m))$
Chisholm-Sosa második axiómája (hun) – second axiom of Chisholm-Sosa (eng)
$\forall m \forall n((\lnot\rel{P}(n,\lnot n)\land\lnot\rel{P}(\lnot n,n))\to\rel{P}(n,\lnot m)\to\rel{P}(m,\lnot m))$
Chisholm-Sosa harmadik axiómája (hun) – third axiom of Chisholm-Sosa (eng)
Ha fenti három formula közül az elsőbe behelyettesítjük az $\rel{I}(m)$ és $\rel{S}(m,n)$ relációk képleteit, akkor egy jóval egyszerűbb, áttekinthetőbb és így könnyebben értelemezhető formulához jutunk.$\forall m \forall n(( \rel{I}(m) \land \rel{I}(n))\to \rel{S}(m,n))$
Chisholm-Sosa módosított első axiómája (hun) – first axiom of Chisholm-Sosa, modified (eng)
A képletet úgy értelmezhetjük, hogy ha két állapot indifferens önmagában, akkor egymáshoz képest ugyanolyan értékűek lesznek. A második és harmadik axióma képletébe is behelyettesítve az $\rel{I}(m)$ reláció formuláját, újra csak egyszerűbb eredményt kapunk. [♦]$\forall m \forall n(( \rel{I}(n) \to \rel{P}(m,n))\to \rel{P}(m,\lnot m))$
Chisholm-Sosa módosított második axiómája (hun) – second axiom of Chisholm-Sosa, modified (eng)
$\forall m \forall n(( \rel{I}(m) \to \rel{P}(n,\lnot m))\to \rel{P}(m,\lnot m))$
Chisholm-Sosa módosított harmadik axiómája (hun) – third axiom of Chisholm-Sosa, modified (eng)
Az első formulát úgy interpretálhatjuk, hogy ha van egy n indifferens állapot, és ebből az következik, hogy egy másik m állapot preferált n-hez képest, akkor az m állapot preferált a saját $\lnot m$ tagadásához képest. A második formula szerint ha az n indifferens állapot létezéséből következik, hogy ez az n állapot preferált egy másik m állapot tagadásához, tehát $\lnot m$-hez képest, akkor az m állapot preferált a saját $\lnot m$ tagadásához képest. Láthattuk tehát, hogy Chisholm és Sosa öt axiómája – egy kivételével – teljesen eltér von Wright elméletétől, de hogy ennek mi az oka, a vitában kinek milyen érvei voltak, erre a kérdésre nem egyszerre és nem is itt válaszolok, hanem az elméletek által kezelt egyes problémákra különö fejezeteket szentelve fogom összehasonlítani a különböző nézőpontokat. Itt érdemes röviden áttekinteni, hogy Bengt Hansson hogyan kezelte a preferenciareláció fogalmát [Bengt] Hansson először megmutatta, hogy mind a von Wright, mind a Chisholm-Sosa szerzőpár által lefektetett elmélet túl erős, és így mindkét elmélet több ponton ellentmond a preferenciareláció mindennapi használatával kapcsolatos intuíciónknak. Ezért Bengt Hansson gyengébb axiómákat vezetett be, bár tanulmánya végén ezekre vonatkozóan is érvényesnek tartotta azt az elvárását, hogy a preferenciák logikájának kidolgozásához talán erősebb logikai nyelvre lehet szükség. Bengt Hansson a preferenciarelációt a 'jobb vagy ugyanolyan jó' értelmeben fogta fel, tehát az $\rel{R}(m,n)$ gyenge preferenciarendezést elemezte, és erre a relációra kikötött két rendezési, illetve két disztribúciós axiómát. Az első bengt hanssoni tétel a tranzitivitás, a második a totalitás tulajdonságát rögzítette. A tranzitivitási feltételt már felvettük a listába, a totalitás formulája így néz ki.$\forall m\forall n(\rel{R}(m,n)\lor\rel{R}(n,m))$
Hansson totalitási kritériuma megfelel a relációk tárgyalása során bemutatott erősen összefüggő tulajdonságnak (☜) a tranzitivitás és totalitás alapján pedig azt mondhatjuk, hogy a bengt hanssoni $\rel{R}$ reláció totális (összefüggő) előrendezés (☜) A következő lépésben Hansson először megmutatta, hogy milyen további tételek vezethetők le a két axiómájából, majd – miután több, túl erős, elfogadhatatlan következményekkel járó változatot kipróbált és elvetett – javasolt két gyengített disztribúciós axiómát.$\forall m\forall n(\rel{R}(m,n)\land\rel{R}(m,o)]\to\rel{R}(m,n \lor o))$
balról disztributív (hun) – left-distributive (eng)
$\forall m\forall n(\rel{R}(m,o)\land\rel{R}(n,o)]\to\rel{R}(m \lor n,o))$
jobbról disztributív (hun) – right-distributive (eng)
A két tétel egy balról és egy jobbról érvényes disztribúciós kritériumot fogalmaz meg. Az első formula azt írja le, hogy ha egy m állapot preferáltabb mint két másik (n vagy o), akkor az m állapot a két másik (n és o) állapot diszjunkciójánál is preferáltabb. A második tétel ennek a fordítottját követeli meg, vagyis azt, hogy ha egy o állapotnál két másik (m vagy n) is preferáltabb, akkor azok konjunkciója is preferáltabb az o állapothoz képest. Beng Hansson hosszan érvelt amellett, hogy végül miért ezeket a tételeket fogadta el, erre én is visszatérek a disztribúciós elv tárgyalásakor. A preferencialogika történetéhez hozzátartozik még, hogy von Wright egy évtizeddel később visszatért a kérdés tárgyalására. Az 1963-as könyvével kapcsolatban megjelent kritikák, alternatív formalizálási kísérletek után újra elővette a preferencia problémakörét, és 1972-ben részben újraformálta elméletét [G.H.v] Saját értékelése szerint nem is annyira a kritikákat fogadta meg, mint saját maga törekedett egyfelől a kérdések egyértelműsítésére, másfelől a válaszok egyszerűsítésére. Tanulmányában von Wright először felsorolta azokat a kérdéseket, amelyeket minél pontosabban tisztázni kell egy preferencialogika kidolgozásakor, majd megállapította, hogy nem igazán lát esélyt arra, hogy ki lehessen dolgozni egy széles körben elfogadott elméletet. Inkább csak azt az állapotot tartotta elérhetőnek, hogy a különböző intuíciók mentén bár szabatos, de párhuzamos értelmezések alakulhassanak ki. Von Wright újra megpróbálkozott a preferencia fogalmának formalizálásával. Von Wright az új elmélet központjába is a $\rel{P}$ szigorú preferenciarendezést tette. Első axiómaként felvette az aszimetrikusságot, másodikként pedig egy új elvet rögzített, amit az (érték)összehasonlíthatóság elvének nevezett el. Ez az összehasonlítható relációtulajdonsággal egyezik meg (☜)$\concept{COMPARABLE}(\rel{P}(m,n))\defi\forall m\forall n \forall o (\rel{P}(m,n) \to (\rel{P}(m,o) \lor \rel{P}(o,n)))$
összehasonlítható (hun) – comparable (eng)
Az összehasonlíthatóság elvének felvétele egyben azt is jelentette, hogy von Wright nem írta elő a – sokat vitatott – tranzitivitás tulajdonságának fennállását, ami viszont a két axiómából már levezethető vált. Ez az alábbi módon látható be:
$1) \;\; \rel{P}(n,o) \to \lnot\rel{P}(o,n)$
$2)\;\; (\rel{P}(m,n)\land \rel{P}(n,o))\to(\rel{P}(m,n)\land\lnot\rel{P}(o,n))$
$3)\;\; (\rel{P}(m,n)\land \rel{P}(n,o))\to((\rel{P}(o,n)\lor \rel{P}(m,o))\land\lnot\rel{P}(o,n))$
$4)\;\; (\rel{P}(m,n)\land \rel{P}(n,o))\to(\rel{P}(m,o)\land\lnot\rel{P}(o,n))$
$5)\;\; (\rel{P}(m,n)\land \rel{P}(n,o))\to\rel{P}(m,o)$
Első lépésben felvesszük a $\rel{P}(n,o)$ aszimmetrikusságát (1. axióma). Második lépésben a kondicionális mindkét oldalát kibővítjük ugyanazzal a $\rel{P}(m,n)$ taggal (Propozicionális Logika: konjunkció bevezetése). Harmadik lépésben a kondicionális jobb oldalán levő $\rel{P}(m,n)$ helyébe behelyettesítjük az összehasonlíthatóság képletének jobb oldalát (2. axióma). Negyedik lépésben elhagyjuk a kondicionális következményéből a jobb oldali $\lnot\rel{P}(o,n)$ összetevőt (PL: konjunkció eliminálása). Ezzel a tranzitivitás képletéhez jutunk. Megállapítható tehát, hogy a $\rel{P}(m,n)$ szigorú preferenciarendezés aszimmetrikus, irreflexív és tranzitív. Ezután von Wright bevezette a $\rel{J}(m,n)$ (gyenge) indifferenciarelációt (valójában az összehasonlíthatatlansági relációt (☜) és az eddig axiómák és tételek alapján levezette, hogy $\rel{J}(m,n)$ reflexív, tranzitív és szimmetrikus reláció. A preferenciarendezés és a gyenge indifferencia reláció segítségével pedig kimondta az (érték)-ekvivalencia elvét, amely az alábbi háromféle állapot lehetőségét tételezi.
$\rel{J}(m,o)\land \rel{J}(o,n)\to \rel{J}(m,n)$
$\rel{P}(m,n)\land \rel{J}(m,o\to \rel{P}(o,n))$
$\rel{P}(m,n)\land \rel{J}(n,o)\to \rel{P}(m,o)$
(érték)-ekvivalencia elve $\rel{P}$-re és $\rel{J}$-re (hun) – principle of (value)-equivalence (eng)
Az ekvivalencia elve az axiómákból levezethető következmény, de önmaga nem axióma. Von Wright az aszimmetricitáson és az összehasonlíthatóságon túl több axiómát már nem definiált, tehát az 1963-as modelljéhez képest jóval gyengébb axiómarendszert javasolt. Úgy tűnik, hogy leginkább Bengt Hansson kritikája hatott leginkább von Wrightre, mert az átalakított modellje sokkal jobban hasonlít Hansson javaslatához, mint akár a saját korábbi, akár Chisholmék elképzeléseihez. Bár von Wright sosem tartotta önálló axiómának a kontrapozíció elvét (☜) de azért megemlítette azt az új tanulmányában. Ezt az elvet Halldén javasolta felvenni a preferencia modelljébe [Soren] Von Wright [G.H.v] nem építette be ugyan az új axiómarendszerébe, de az a tény, hogy alkalmazta, arra utal, hogy úgy gondolta, a preferenciára vonatkozóan érvényesnek lehet tartani. Ezt az elvet Chisholm és Sosa támadta (akkor elsősorban mint Halldén javaslatát), de hogy miért és hogyan kritizálták a kontrapozíció elvét, azt később mutatom be (☜) Egyelőre álljon itt magának az elvnek a formulája.$\forall m\forall n(\rel{P}(m,n)\leftrightarrow((\rel{P}(\lnot n,\lnot m)))$
kontrapozíció elve (hun) – principle of contraposition (eng)
Az 1972-es tanulmányában von Wright nagy teret szentelt annak, hogy megmutassa, miként lehet leírni a lehetséges világ szemantika alapján a ceteris paribus preferencia fogalmát. Erre a kérdésre külön fejezetben térek ki (☜) ezért itt nem tárgyalom. Von Wright a cikke végén nekifutott újra annak a feladatnak, hogy hogyan lehet az olyan monadikus fogalmat, mint a 'jó' vagy a 'rossz' kategóriája definiálni a 'jobb' fogalom segítségével: az előbbi kettőt érték-abszolút, az utóbbit összehasonlító-érték fogalomnak tartotta, és másként definálta őket az 1963-as megoldásához képest [G.H.v] Von Wright felvetette, hogy a jó és a rossz fogalmának meghatározásához G.E. Moore üres világ (empty world) fogalmára lehetne támaszkodni, csak ehhez tisztázni kéne, mit is jelent pontosan ez a fogalom. Von Wright javaslata az volt, hogy az üres világ fogalmát az ellentmondással (☜) lehetne definiálni, mert az logikailag lehetetlen világ, ahol semmi sem igaz és semmi sem hamis. Ezt a világot a lehetséges világok sorában a nulladiknak tekintve (0-világ) és $w_0$-val jelölve olyan fogalomhoz jutunk von Wright szerint, amely alapján mondhatjuk, hogy jó az a $w_x$ világ, amelyre igaz, hogy $\rel{P}(x,0)$, rossz az a $w_y$ világ, amelyre igaz, hogy $\rel{P}(0,y)$. Mindezt a totális állapotokra írhatnánk így. Egy tetszőleges egyedi m állapotra vonatkoztatva a jót és a rosszat a következőképpen határozhatnánk meg: $\rel{P}_C(m,0)$ a jó, $\rel{P}_C(0,m)$ pedig a rossz definíciója.Preferenciastruktúra
Az eddigiekből már kiderülhetett, de tézisszerűen még nem mondtam ki, hogy a preferencia jelenségét nem egyetlen, hanem inkább több preferenciareláció segítségével írhatjuk le igazán. Első nekifutásra tán még tűnhetne úgy, hogy a preferenciarendezés fogalma jelenti a jelenség lényegét, de ez nem így van. A különböző preferencialogikák már abban is különböznek, hogy a szigorú vagy a gyenge preferenciarendezést teszik-e az elmélet középpontjába. De kiderült az is, hogy az indifferencia vagy az összehasonlíthatatlansági relációknak is olykor komoly szerepe van. Az elméletek ezért mozdultak el abba az irányba, hogy ne egyik vagy másik preferenciarelációról beszéljünk, hanem preferenciastruktúráról. Ez annyit jelent, hogy egyfelől általában vett preferenciarelációról beszélünk, és megkülönböztetjük egymástól ennek típusait ($\rel{R}$ gyenge és $\rel{P}$ erős rendezés, $\rel{I}$ indifferencia, $\rel{J}$ összehasonlíthatatlanság) [♦] másfelől ezeket a preferenciareláció-típusokat, valamint a köztük értelmezett műveleteket egy struktúrába összefogva beszélünk preferenciastruktúráról. Kiindulásként vegyünk egy A (tartó)halmazon értelmezett ($\rel{P}$, $\rel{I}$, $\rel{J}$) preferenciastruktúrát, és nézzük meg, milyen tulajdonságokat definiálhatunk ezen a struktúrán [M.Rou]$\concept{IRREFLEXIVE}(\rel{P}) \;\land\; \concept{REFLEXIVE}(\rel{I}) \;\land\; \concept{IRREFLEXIVE}(\rel{J})$
$\rel{P}$ és $\rel{J}$ irreflexív, $\rel{I}$ reflexív
$\concept{ASYMMETRICAL}(\rel{P})\;\land\; \concept{SYMMETRICAL}(\rel{I}) \;\land\;\concept{SYMMETRICAL}(\rel{J})$
$\rel{P}$ aszimmetrikus, $\rel{I}$ és $\rel{J}$ szimmetrikus
$\rel{P}\cap\rel{I}=\emptyset \;\land\; \rel{P}\cap\rel{J}=\emptyset \;\land\; \rel{I}\cap\rel{J}=\emptyset $
$\rel{P}$, $\rel{I}$ és $\rel{J}$ kölcsönösen kizárják egymást
$\rel{P}\cup\rel{P}^{- 1} \cup\rel{I}\cup\rel{J}=A\times A $
$\rel{P}$ és a konverze ($\rel{P}^{- 1}$), $\rel{I}$ és $\rel{J}$ együttesen kiadják a tartóhalmazon vett egész relációt
Az első két tétel azokat a relációtulajdonságokat rendeli a relációkhoz, amelyeket már korábban megismertünk. Fontos összefüggést fejez ki a harmadik tétel, miszerint a három alapreláció diszjunktnak tekinthető egymáshoz képest. Végül a negyedik tételből kiderül az is, hogy ha a három alaprelációhoz hozzávesszük még a szigorú rendezés konverzét, akkor a négy reláció teljesen lefedi a tartóhalmazon értelmezhető teljes relációt. Mivel bizonyítható az is, hogy az $\rel{P}$ rendezés konverze is diszjunkt az indifferencia és összehasonlíthatatlansági relációkkal, így kijelenthető, hogy a ($\rel{P}$, $\rel{P}^{- 1}$, $\rel{I}$, $\rel{J}$) preferenciastruktúrában a négy reláció teljes partíciót alkot. [♦] Sem a hármas, sem a négyes relációstruktúrában nem szerepel az $\rel{R}$ gyenge rendezési reláció. Ezt azonban könnyen pótolhatjuk az alábbi összefüggés alapján.$\rel{R}=\rel{P}\cup\rel{I}$
A új rendezési reláció segítségével további összefüggéseket is megállapíthatunk a hármas struktúra elemei és a gyenge rendezés között. Ehhez használnunk kell a konverzreláció (☜) a duálreláció (☜) és a komplementer reláció (☜) valamint a teljesség vagy erős összefüggőség (☜) és az üres reláció (☜) fogalmát. Először a hármas struktúra elemeit írhajuk fel a gyenge rendezési reláció segítségével, majd a gyengerendezés teljességére adhatunk meg egy új feltételt.$(\rel{P}, \rel{I}, \rel{J}) = (\rel{R}\cap\rel{R}^{- d}, \rel{R}\cap\rel{R}^{- 1}, \overline{\rel{R}}\cap\rel{R}^{- d})$
az ($\rel{I}$, $\rel{J}$, $\rel{R}$) relációstruktúra elemei az $\rel{R}$ segítségével kifejezve
$\concept{STRONGLY\_CONNECTED}(\rel{R}) \leftrightarrow \rel{J}=\underline{\rel{E}}$
az $\rel{R}$ gyenge preferenciarendezés erősen összefüggő, ha $\rel{J}$ üres
A bemutatott összefüggések alapján belátható az is, hogy a preferenciafogalmakra ráhúzhatjuk a logikai hatszög sematizmusát.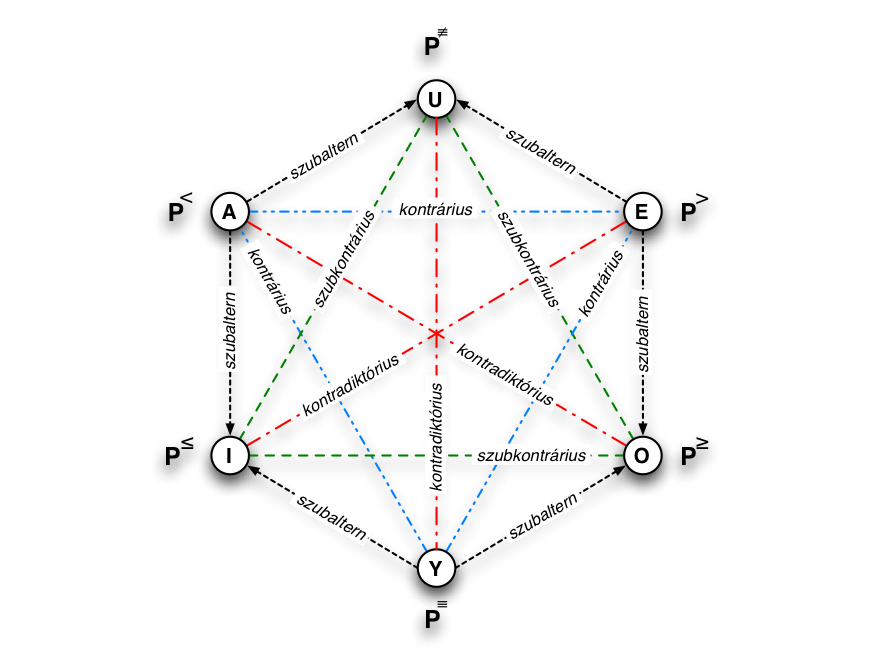
A preferenciahatszögben nem szerepel az összehasonlíthatatlansági reláció, viszont szerepel az indifferencia kontradiktorikus ellentéte, nevezhetnénk ezt differencia relációnak is, ha már nem lenne ilyen néven egy különbözőségi relációnk (☜) Ennek az az oka, hogy a preferenciareláció fogalmára lehet a logikai hatszöget "ráfeszíteni", ami viszont még nem adja ki a teljes relációt (☜) A preferenciareláció alá sorolhatjuk a fenti hat preferenciareláció-típust, és ezek közül három-három reláció mindig kiadja a teljes preferenciarelációt. Igaz például a következő összefüggés: $\rel{P}^{>} \cup \rel{P}^{\equiv} \cup \rel{P}^{<}=\rel{P}$. Az univerzális relációt azonban csak úgy kaphatjuk meg, ha a preferenciarelációhoz hozzáadjuk még az összehasonlíthatatlansági relációt is.
Preferencia és reflexivitás
A preferenciaelméleteken belül nem igazán szokás reflektálni a reflexivitás kérdésére. Ez talán magyarázható azzal, hogy a reflexivitás részben összefügg olyan más tulajdonságkörökkel (például a szimmetricitással, az összekapcsoltsággal), amelyeket viszont mindig sokkal nagyobb figyelemmel kísértek. Az irreflexivitás több más relációtulajdonságból is következik. Például az aszimmetrikus reláció vagy az összefüggő reláció mindig irreflexív (☜) Von Wright sohasem vette fel az axiómarendszerébe a reflexivitás tulajdonságát, de több helyen is kategórikusan kijelentette, hogy az intrinzikus preferenciának irreflexívnek kell lennie mondván: "egy állapot sem lehet jobb önmagánál" [G.H.v] A reflexivitás direkt tárgyalását tekintve az egyetlen kivételt talán az jelenti, hogy a preferenciastruktúrák tárgyalásakor felveszik az axiómák közé a preferenciarelációk reflexivitási tulajdonságait.Preferencia és szimmetricitás
Az aszimmetrikusság feltételezése nagyon erős, sokan nem is fogadják el. A von wrighti axióma elfogadása azt jelenti, hogy két világállapot összehasonlításakor mindig valamelyiket szigorúan jobbnak találjuk a másiknál. Azok, akik ezt a tulajdonság tételezik, azok a szigorú preferenciát teszik az elméletük középpontjába. Ezzel szemben azok, akik a gyenge preferencia fogalmát tartják alapvetőnek, és arra alapozzák elméletüket, azok a gyenge preferenciához szükséges antiszimmetrikus tulajdonság (☜) létezését írják elő. Bármelyiket is vesszük fel a modellünkbe kiindulásként, könnyen levezethető az egyik fogalom a másikból, ezért nagy jelentősége nincs választásnak. Mivel ezt korábban még nem rögzítettük, érdemes itt felvenni a tételek közé a gyenge preferencia antiszimmetrikusságát.$\concept{ANTISYMMETRIC}(\rel{R}) $
$\rel{R}$ antiszimmetrikus (hun) – $\rel{R}$ antisymmetric (eng)
A szimmetrikusság egyik preferenciarendezésnél sem jöhet szóba, viszont – ahogy azt már korábban rögzítettem – mind a közömbösségi, mind az összehasonlíthatatlansági reláció szimmetrikus.Preferencia és összefüggőség
Von Wright nem foglalkozott a teljesség tulajdonságával, a Chisholm és Sosa páros sem, Bengt Hansson viszont a totalitás tulajdonságát felvette az axiómái közé (☜) Bár Bengt Hansson elméletében fontos szerepe van a totalitás tételezésének, [♦] ettől még Sven Ove Hansson igaza van, amikor azt állítja, hogy preferencialogikában általában nem követelik meg ezt a tulajdonságot. Meg is magyarázta, miért. Azért nem, mert ez a feltétel nagyon erős elvárást teremt, ami sokszor nem vagy csak nagyon nehezen teljesíthető. De miért is kéne teljesülnie? Ha valaki preferálja m-t mind n-nel, mind o-val szemben, akkor tud választani, miért kéne foglalkoznia azzal, hogy n és o közül melyiket preferálja inkább. Még konkrétabban: ha autót akarunk vásárolni, és két lehetőség között ingadozunk, akkor az ezek közti döntéshez nincs szükségünk arra, hogy állást foglaljunk a további húsz kocsivásárlási lehetőséggel kapcsolatban. Elméleti szempontokból azonban sokat jelent, ha valahol kimondhatjuk a teljesség fennállását, ezért a formális elméletek szeretik ezt a tulajdonságot (lásd Bengt Hansson). Sven Ove Hansson röviden kitér arra a kérdésre, hogy mit lehet tenni, ha egy halmazon nem teljes a rendezés (incomplete), és teljesé akarjuk azt tenni. Három kimenet lehetséges: vagy egyértelműen megoldható (unique resolvable), amikor egyetlen elrendezést kapunk, vagy többféleképp megoldható (multiply resolvable), amikor többféle rendezést kapunk, vagy megoldhatatlan (irresolvable), amikor nem jutunk teljes rendezéshez. Utóbbira példa: választani a gázai piramis lerombolása vagy a pandák kihalása között. Az első két eset S.O. Hansson összehasonlíthatatlannak (incomparable), a harmadikat inkommenzurábilisnak (incommensurable) nevezi [SvenO]Preferencia és a disztribúció elve
A negyedik von wrighti axióma, a disztribúció elve (☜) azzal a kérdéssel kapcsolatos, hogy miként működik a preferencia a diszjunkció esetén, vagyis akkor, amikor úgy kell a dolgokat összehasonlítani, hogy az állapotok diszjunktív kapcsolatban lehetnek egymással. Von Wright erre azt a példát adta, hogy a munkahelyén valakinek döntenie kell arról, hogy mit preferál jobban: a fizetésemelést (m) vagy hosszabb éves szabadságot (n) a napi munkaidő csökkentéshez (o) képest. A kérdés, hogy mit lehet mondani az ilyen összetett állapotokra vonatkozóan ($(m \lor n)$ az o-val szemben). Von Wright ilyen-olyan feltételezések és levezetések után hozta ki azt formulát, amit végül axiómának minősített.$\forall m\forall n \forall o \forall p(\rel{P}(m\lor n,o\lor p)\leftrightarrow(\rel{P}(m\land\lnot o \land\lnot p,\lnot m \land\lnot n \land o)\land$ $\rel{P}(m \land\lnot o \land\lnot p,\lnot m\land\lnot n\land p)\land$ $\rel{P}(n \land\lnot o\land\lnot p,\lnot m \land\lnot n \land o)\land$ $\rel{P}(n \land\lnot o \land\lnot p,\lnot m \land\lnot n \land p)))$
Nyugodtan mondhatjuk, hogy sokadik ránézesre sem tűnik intuitívnek a formula. Ebben a formájában nehéz befogadható értelmezést adni neki. Pedig van. Több más szerző mellett Patrick Girrard is újraértelmezte, leegyszerűsítette az eredeti von wrighti formulát és megmutatta, hogyan azt le lehet vezetni a konjunktív expanzió elvének és a jóval egyszerűbb disztributivitási tulajdonságoknak a felhasználásával [Patri] Az átalakítás eredményeként a von wrighti formula két egyszerűbb és érthetőbb formulára visszavezethető.
$\forall m\forall n \forall o (\rel{P}(m\lor n,o)\leftrightarrow(\rel{P}(m,o) \land \rel{P}(n,o)))$
\rel{P} preferenciareláció a diszjunkcióra jobbról konjunktíve disztributív
$\forall m\forall n \forall o (\rel{P}(m,n\lor o)\leftrightarrow(\rel{P}(m,n) \land \rel{P}(m,o)))$
\rel{P} preferenciareláció a diszjunkcióra balról konjunktíve disztributív
A fenti képletek alapján már az is megállapítható, hogy a von Wright által megfogalmazott disztribúciós axiómák meglepően közel vannak Bengt Hansson axiómáihoz (☜) Az egyszerűsített von wrighti formulákhoz képest a hanssoni disztribuciós feltételek csak annyiban gyengébbek, hogy amíg az utóbbiak csak az egyik irányban érvényesek, tehát csak kondicionális művelet kapcsolja össze a két tagmondatot, addig az előbbi esetben kétirányú kapcsolatot ír le a bikondicionális logikai kapcsoló.
$\forall m \forall n \forall o ((\rel{R}(m,n)\land\rel{R}(m,o))\to\rel{R}(m,n \lor o)))$
$\forall m\forall n \forall o ((\rel{R}(m,o)\land\rel{R}(n,o))\to(\rel{R}(m \lor n,o)))$
Persze azért van egy másik különbség is közöttük, csak azt talán kicsit nehezebb észrevenni. Különböznek abban, hogy amíg von Wright a $\rel{P}(m,n)$ szigorú preferenciára, addig Bengt Hansson az $\rel{R}(m,n)$ gyenge preferenciára mondta ki a disztributivitási axiómáit. Tanulságos egyébként az a mód is, ahogy Bengt Hansson eljutott az axiómáihoz. Először értékelte az erős disztribúciós axiómákat, majd meggyőző példákkal igazolta, hogy ezek elfogadása intuícióinkkal ellentétes következményekkel járna [Bengt] Első lépésben Hansson feltette, hogy a következő formulát kellene elfogadnunk.
$\forall m\forall n \forall o \forall p(\rel{P}(m\lor n,o\lor p)\leftrightarrow (\rel{F}(m,n,o,p)\veebar \rel{F}(n,m,o,p)\veebar \rel{F}(m,n,p,o) \veebar \rel{F}(n,m,p,o)))$
A formula jobb oldalán látható négy argumentumú $\rel{F}$-operátor azt fejezi ki, hogy az argumentumokba írt négy alternatíva az adott preferenciasorrendbe rendezhető. A formula intuitívnak tűnik, hiszen annyit fejez ki, hogy az első két alternatív diszjunkcióját jobbnak értékeljük a második két alternatíva diszjunkciójához képest, akkor az egyenkénti összehasonlítás során az első két alternatíva előbbre kell, hogy kerüljön a második két alternatívánál (illetve fordítva). Másként: ha a bal oldalon kifejezett preferenciarendezés fennáll, akkor a jobb oldali képlet négy komponense közül az egyiknek kell teljesülnie. Valóban úgy tűnik, hogy ez a feltételezés elfogadható. B. Hansson azonban a fenti formulából levezet egy abból következő tételt, amiről viszont egy ellenpéldával bebizonyítja, hogy vállalhatatlan értelmezést is lehetővé tesz. A levezetett tétel így néz ki:
$\forall m\forall n \forall o (\rel{I}(m,n)\to\rel{I}(m \lor o,n\lor o))$
A képletben az $\rel{I}(m,n)$ indifferenciareláció szerepel (amit Bengt Hansson $\rel{S}(m,n)$ 'same as' relációnak nevez). Az alapfeltételezésből logikailag következő tétel azonban túl erős, és vállalhatatlan következményekkel jár. Ezt Hansson a következő példával szemlélteti. Tegyük fel az alábbiakat.
| $m$ | valaki megnyeri a fődíjat az ötös lottón | |||||||||||||
| $n$ | valaki megnyeri a fődíjat a hatos lottón | |||||||||||||
| $o$ | valaki nyer egy kettest az ötös lottón | |||||||||||||
| $m\lor o$ | valaki megnyeri a fődíjat és nyer egy kettest az I. lottón | |||||||||||||
| $n\lor o$ | valaki megnyeri a fődíjakat mind az ötös, mind a hatos lottón | |||||||||||||
$\forall m\forall n \forall o \forall p ((\rel{I}(m,n)\land \rel{I}(o,p)) \to \rel{I}(m \lor\lnot n,o\lor\lnot p))$
A formula úgy értelmezhető, hogy ha van két-két állapot (m és n, illetve o és p), amelyek páronként egyforma értékesek ($\rel{I}(m,n)$ és $\rel{I}(o,p)$), akkor a két állapotpárból képzett két-két speciális diszjunktív állapot ($(m \lor\lnot n)$ és $(o \lor\lnot p)$) is ugyanolyan értékűek. Azonban ez a tétel sem maradhatott meg, mert Hanssonnak erre is akadt ellenpéldája. A történet részben megint a lottózásról szól, de most más alternatívák kerülnek a lottónyeremények mellé. Ezeket mutatom be a következő táblában.
| $m$ | valaki 100 millió forintot nyer az ötös lottón | |||||||||||||
| $n$ | valaki 100 millió nyer a hatos lottón | |||||||||||||
| $o$ | valaki meghal egy balesetben, mert elüti egy zöld busz | |||||||||||||
| $p$ | valaki meghal egy balesetben, mert elüti egy kék busz | |||||||||||||
| $m$ | a kutyája jól van | |||||||||||||
| $n$ | a fia jól van | |||||||||||||
| $o$ | a lánya jól van | |||||||||||||
| $p$ | a felesége meghalt autóbalesetben | |||||||||||||
$1)\;\; \rel{R}(m,n\lor (o\land p))$
$2)\;\; \rel{R}(m,(n\land p) \lor o))$
$3)\;\; \rel{R}(m,(n\lor (o\land p)) \lor ((n\land p) \lor o))$
$4)\;\; \rel{R}(m,(n\lor (o)) \lor ((n) \lor o))$
$5)\;\; \rel{R}(m,(n\lor o))$
Kiindulásként két preferendezést állított fel Hansson diszjunktív állapotok között. A fenti első sor ($\rel{R}(m,n\lor (o\land p))$) azt fejezi ki, hogy jobb az a hír, mely szerint 'a kutyája jól van' ahhoz az összetett hírhez képest, hogy 'a fia jól van (n) vagy a lánya jól van, de a felesége meghalt' ($o \land p$). A rossz hír jelenléte a diszjunkció jobb oldali tagjában az egész jobb oldali relátumot ($n\lor (o\land p)$) diszpreferálta. Ugyanez igaz a második sorra is a megfelelő módosításokkal. A harmadik sor formulájához az első disztribúciós axióma alkalmazásával juthatunk, amikoris az axióma képletébe behelyettesítjük a fenti két sort, mint az axióma bal oldali konjunkciójának két elemét. A harmadik formulából úgy kapjuk meg a negyediket, hogy kétszer alkalmazzuk a belső konjunkciókra a konjunkció eliminálásának műveletét (☜) Ennek eredményeként elhagyhatjuk a belső konjunkciók p-t tartalmazó tagjait. A negyedik sor formuláját sima propozíciólogikai egyszerűsítésekkel "kitisztíthatjuk", így jutunk az ötödik formulához. Ez viszont olyat állít, ami intuícióellenes, hiszen a $\rel{R}(m,(n\lor o))$ formula annyit jelent, hogy az illető jobban örülne annak a hírnek, hogy 'jól van a kutyája' ahhoz képest, hogy 'jól van a fia vagy a lánya'. Feltételezhetjük ugyan, hogy lehetnek ilyen beállítódású személyek is, de semmiképpen sem ezt az attitűdöt tartjuk általánosnak, ezért ezt a következtetést mint kontraintuitív végeredményt nyugodtan "elutasíthatjuk". Bengt Hansson rezignált végkövetkeztetése ezekután csak az, hogy a két disztribúciós axiómát nem lehet feltétel nélkül alkalmazni.
Preferencia és a kontrapozíció elve
A témakör felvezetésekor említettem, hogy Sören Halldén felvette a posztulátumai közé a kontrapozíció elvét (☜) Von Wright az 1963-as esszéjében még nem beszélt róla, de az 1972-es cikkében már igen, és noha az elvet nem vette fel az új axiómarendszerébe, az intuícióinkkal megegyezőnek és ezért – legalább részben – elfogadhatónak tartotta. Tette ezt annak ellenére, hogy előbb a Chisholm és Sosa szerzőpár [Roder] majd Bengt Hansson is meggyőző példákat hozott arra, hogy feltétel nélkül nem szabad elfogadni ezt az elvet [Bengt] Chisholm és Sosa ellenpéldája nem annyira a hétköznapi élet problémateréből merített, de ettől még a belőle kibontható kellemetlen logikai következmény fel- és elismerhető. Két állítást mutattak be arra, hogyan kellene összehasonlítani állításokat, illetve azok tagadásait egymással.| $m$ | vannak boldog kócsagok | |||||||||||||
| $n$ | vannak kövek | |||||||||||||
| $\lnot m$ | nincsenek boldog kócsagok | |||||||||||||
| $\lnot n$ | nincsenek kövek | |||||||||||||
| $m$ | valaki első díjat nyer | |||||||||||||
| $n$ | valaki valamilyen díjat nyer | |||||||||||||
| $\lnot m$ | valaki nem nyer első díjat | |||||||||||||
| $\lnot n$ | valaki semmilyen díjat sem nyer | |||||||||||||
| $m$ | $A$-nak két példánya van Rousseau Társadalmi szerződéséből | |||||||||||||
| $n$ | $A$-nak egy példánya van Rousseau Társadalmi szerződéséből | |||||||||||||
| $\lnot m$ | $A$-nak nincs két példánya Rousseau Társadalmi szerződéséből | |||||||||||||
| $\lnot n$ | $A$-nak nincs példánya Rousseau Társadalmi szerződéséből | |||||||||||||
$\forall m\forall n(\rel{P}(m,n)\leftrightarrow(((m\land \lnot n)\ne\bot \land (\lnot m \land n)\ne\bot)\to\rel{P}(\lnot n,\lnot m)))$
ellentmondásmentes kontrapozíció elve (hun) – principle of contradiction-free contraposition (hun)
Ugyan a fenti tétel a szigorú preferenciarendezésre vonatkozik, de ugyanúgy ki lehet mondani az indifferenciarelációra nézve is. Ezzel a szűkítéssel már elkerülhetjük a kontrapozíció elvének ellentmondásait – gondolhatnák, de nem így van. Annak bizonyságára, hogy semmi sem olyan egyszerű, mint ahogy látszik, a Sven Ove Hansson által javasolt, fenti szűkítve-pontosító definíció után bemutatok egy példát, amely ellentmondani látszik az ellentmondásmentes kontrapozíció elvének [SvenO] Képzeljük el az alábbiakat.| $m$ | valaki felajánl 100 dollárt jótékony célokra | |||||||||||||
| $n$ | valaki felajánl 50 dollárt jótékony célokra | |||||||||||||
| $\lnot m$ | valaki nem ajánl fel 100 dollárt jótékony célokra | |||||||||||||
| $\lnot n$ | valaki nem ajánl fel 50 dollárt jótékony célokra | |||||||||||||
| $m$ | nyerünk 2 milliárd 5 forintot a lottón | |||||||||||||
| $n$ | nyerünk 1429 forintot a lottón | |||||||||||||
| $\lnot m$ | nem nyerünk 2 milliárd 5 forintot a lottón | |||||||||||||
| $\lnot n$ | nem nyerünk 1429 forintot a lottón | |||||||||||||
a konjuktív expanzió és a kontrapozíció elve logikailag azonos
$1)\;\; \rel{P}(m,n)=\rel{P}(m \land \lnot n,\lnot m \land n)$
$2)\;\; \rel{P}(m,n)=\rel{P}(\lnot n \land m,n \land \lnot m)$
$3)\;\; \rel{P}(m,n)=\rel{P}(\lnot n \land \lnot\lnot m,\lnot\lnot n \land \lnot m)$
$4)\;\; \rel{P}(m,n)=\rel{P}((\lnot n) \land \lnot(\lnot m),\lnot(\lnot n) \land (\lnot m))$
$5)\;\; \rel{P}(m,n)=\rel{P}((\lnot n),(\lnot m))$
$6)\;\; \rel{P}(m,n)=\rel{P}(\lnot n,\lnot m)$
Az első sor mutatja a konjunktív expanzió elvét. A második sorban csak megcseréltük a konjunkciók összetevőinek sorrendjét. A harmadik lépésben betettünk egy-egy kettős tagadást, ami – mint tudjuk – nem változtat az igazságértékeken. A negyedik sorban zárójellel határoltuk el mindegyik változó negáltját, és az így képzett "új" változókra (tehát a $\lnot m$-re és az $\lnot n$-re) nézve újra alkalmaztuk a konjuktív expanzió elvét ("visszafele"). Így kaptuk az ötödik sor formuláját, amiből már csak a fölösleges zárójeleket kellett elhagyni, hogy a hatodik sorban láthassuk a kontrapozíció törvényének képletét. Ez alapján mindazt, amit a kontrapozícióval kapcsolatban bemutattam, elmondhatnám a konjunktív expanzió elvével kapcsolatban is. Még azt is mondhatnánk, hogy szükségtelen a konjunktív expanzió elvének önálló tárgyalása, de ez nem így van. Látni fogjuk, hogy további, eddig még nem tárgyalt problémákkal kerülünk szembe a következő fejezetben. Logikai szempontból valóban nem lenne szükség a konjuktív expanzió elvének elemzésére, de gyakorlati megfontolások miatt mégis érdemes megtenni ezt. Egyszerűen azért, mert a logikailag ekvivalensnek tekinthető "jelenségekre" másfajta nézőpontból közelítünk, és ez – legalább részben – másfajta kép kialakításához, másfajta összefüggések felismeréséhez segíthet minket.
Preferencia és a konjunktív expanzió elve
Von Wright harmadik axiómája, a konjunktív expanzió elve (☜) az (állapot)változások és a preferencia között állapít meg összefüggést. Von Wright abból indult ki, hogy a két állapot (m és n) együttes figyelembe vételével négyféle, egymást kölcsönösen kizáró világállapot lehetséges:$(m\land n) \veebar (m\land \lnot n) \veebar (\lnot m\land n) \veebar (\lnot m \land \lnot n)$
"De ha magukat meg nem tartóztathatják, házasságban éljenek: mert jobb házasságban élni, mint égni." (Pál Apostolnak Korinthusbeliekhez írt első levele, 7.9)
Vagyis – ahogy Casta$\rm \tilde{n}$eda értelmezi – "jobb házasságban élni és nem égni, mint nem házasságban élni és égni." Ha az összehasonlítást (választás) így értelmezzük, akkor szükségesnek látszik a konjunktív expanzió elve. Ezzel azonban nem mindenki van így. Chisholm és Sosa például elutasította ezt az elvet [Roder] A kócsagos példájukat kicsit átalakítva a következő alternatívákat ajánlották összehasonlításra.| $m$ | vannak kövek | |||||||||||||
| $n$ | vannak boldogtalan kócsagok | |||||||||||||
| $m \land \lnot n$ | vannak kövek és vannak boldog kócsagok | |||||||||||||
| $\lnot m \land n$ | nincsenek kövek és nincsenek boldog kócsagok | |||||||||||||
| $m$ | nincs három boldog görög | |||||||||||||
| $n$ | van két boldogtalan római | |||||||||||||
| $m \land \lnot n$ | nincs három boldog görög és nincs két boldogtalan római | |||||||||||||
| $\lnot m \land n$ | van három boldog görög és van két boldogtalan római | |||||||||||||
| $m$ | nyerek 100 millió forintot a lottón, és tartozom valakinek 2000 forinttal | |||||||||||||
| $n$ | tartozom valakinek 2000 forinttal | |||||||||||||
| $m \land \lnot n$ | nyerek 100 millió forintot a lottón, és tartozom valakinek 2000 forinttal, és nem tartozom valakinek 2000 forinttal | |||||||||||||
$\forall m\forall n (\rel{P}(m,n)\leftrightarrow(m\land\lnot n=\bot\to\rel{P}(m, \lnot m \land n)) \veebar (m\land\lnot n\ne\bot\to\rel{P}(m \land\lnot n, \lnot m \land n)))$
ellentmondásmentes konjunktív expanzió elve (hun) – principle of contradiction-proof conjunctive expansion (eng)
Ez az ellentmondásmentes szűkítés hasonlít a kontrapozíció elve esetében alkalmazott megoldáshoz, amit már nyilván nem tarthatunk véletlennek annak ismeretében, hogy a konjunktív expanzió és a kontrapozíció elvei logikailag ekvivalensnek tekinthetőek. Kiderült azonban, hogy ez a szűkítés még mindig nem elég. Sven Ove Hansson mutatott egy olyan példát, ami miatt az ellenmondásmentes konjunktív expanzió elvét még tovább kellett pontosítani [SvenO] Lássuk a példát!| $m$ | valaki utazik a Holdra | |||||||||||||
| $n$ | valaki űrhajóval utazik | |||||||||||||
| $m \land\lnot n$ | valaki utazik a Holdra és nem űrhajóval utazik | |||||||||||||
| $\lnot m \land n$ | valaki nem utazik a Holdra és űrhajóval utazik | |||||||||||||
$\forall m\forall n (\rel{P}(m,n)\leftrightarrow((\Box(m\land\lnot n)\to \Box\Box(m\land\lnot n)) \to\rel{P}(m, \lnot m \land n)) \veebar (\Box(m\land\lnot n)\to \Box\Box(m\land\lnot n)) $
$\to\rel{P}(m \land\lnot n, \lnot m \land n)))$
ellentmondásbiztos konjunktív expanzió elve (hun) – principle of contradiction-proof conjunctive expansion (eng)
Ha ezt a kiegészítést megtettük, akkor természetesen ezt a második szűkítést érdemes elvégeznünk a kontrapozíció elvére vonatkozóan is. Így az alábbi módosított formulához jutunk.$\forall m\forall n(\rel{P}(m,n)\leftrightarrow(((\Box(m\land \lnot n) \rightarrow \Box\Box(m\land \lnot n)) \land (\Box(\lnot m \land n)\to \Box\Box(\lnot m \land n)))\to\rel{P}(\lnot n,\lnot m)))$
ellentmondásbiztos kontrapozíció elve (hun) – principle of contradiction-proof contraposition (hun)
A konjunktív expanzió és a kontrapozíció elveinek kétszeres pontosítása után visszatérhetünk Chisholm és Sosa legelső kócsagos példájához (☜) Sven Ove Hansson szerint ha a példára kétféleképpen is alkalmazzuk a konjunktív expanzió elvét (azaz a kontrapozíció bal- és jobb oldalára egyaránt rávetítjük a konjunktív expanzió képletét), akkor belátható, hogy Chisholmék példája nem tartalmaz ellentmondást – akkor sem, ha a "hétköznapi intuíciónk" számára ez nehezebben befogadható [SvenO]Preferencia és választás
Bár a von wrighti konjuntív expanzió elvével kapcsolatban írt tanulmányt R.E. Jennings [Jenni] mégsem az elvről szóló fejezetben foglalkozom Jennings véleményével, hanem a választás és preferencia kapcsolatát taglaló részben. Ennek az az elsődleges oka, hogy Jennings nem a korábban kifejtettek értelemben szólt hozzá a konjunktív expanzió elvéhez, hanem csak azt állította, ez tulajdonság nem a preferenciarelációt, hanem a választás (choice) jelenségét jellemzi. Jennings szerint ha m-t preferálom n-nel szemben, akkor az azt is kell, hogy jelentse, hogy van valamilyen tapasztalatom mind az m-mel, mind az n-nel kapcsolatban. Valaminek a megtapasztalása azonban még nem jelenti automatikusan azt is, hogy tudnánk, milyen lehet annak a valaminek a hiánya, ezért erre nem is hivatkozhatunk az összehasonlítások során. Az explikáció érdekében Jennings elkülönített kétféle preferenciafogalmat, és ezeket $\rel{P}^j$-preferencia és $\rel{R}^j$-preferencia kifejezésekkel jelölte. [♦] Mindkét esetben ugyanazt a helyzetet értelmezzük:valaki az m alternatívát preferálja n-nel szemben
Azonban amíg a $\rel{P}^j$-preferenciával azt az értelmezést fejezzük ki, hogy:valakinek jobban tetszik az m, mint az n-t
addig $\rel{R}^j$-preferencia segítségével azt reprezentáljuk, hogy:valaki inkább szeretné m-t, mint az n-t
Jennings szerint a két értelemzés abban különbözik egymástól, hogy amíg az előbbiben nincs semmilyen akarati tényező, addig az utóbbiban van, és így az előbbi valóban a preferenciát mint tetszést, az utóbbi pedig inkább a preferenciát mint választást (choice) reprezentálja. Ez a külünbség megnyilvánul abban (is), hogy a preferencia esetében nem érvényes a konjunktív kiterjeszthetőség elve, míg a választás esetében igen. A kétféle reláció további két fontos szempontból is eltér egymástól. Egyfelől különböznek a magyarázatokban betöltött szerepük tekintetében, másfelől más előfeltételekkel élünk akkor, amikor a kétféle relációt tulajdonítjuk valakinek. A $\rel{P}^j$-preferencia és $\rel{R}^j$-preferencia aszimmetrikus viszonyban állnak egymással abban az értelemben, hogy az utóbbiakat mindig megmagyarázhatjuk az előbbiekre hivatkozva, de ez a lehetőség fordítva már nem áll fenn. Jennings példájával élve arra a kérdésre, hogy:— Miért kéne neked inkább a narancs, mint mandarin?
adhatunk olyan magyarázatot, hogy egyszerűen hivatkozunk arra:— Mert jobban szeretem a narancsot a mandarinnál.
de arra kérdésre, hogy:— Miért szereted jobban a narancsot a mandarinnál?
nem tudunk értelmesen azzal válaszolni, hogy utalunk a vonatkozó $\rel{R}^j$-preferenciánkra. A másik különbség a jenningsi $\rel{P}^j$- és $\rel{R}^j$-preferenciák között abban van, hogy milyen fokú és milyen típusú magyarázatot fogadunk el, amikor meg akarjuk indokolni őket. A $\rel{P}^j$-preferencia esetén az előző kérdésre elfogadjuk az alábbi választ:— Hát, csak.
Ebben az esetben a magyarázat lényege az, hogy egyszerűen hivatkozhatunk a létező $\rel{P}^j$-preferenciánkra: "ezt szeretjük jobban". Itt nincs racionális magyarázat, nincs érvelés, nincs megokolás, nincs másra hivatkozás, csak a preferencia "puszta" deklarálása. Ezzel szemben a $\rel{R}^j$-preferencia esetén mindig kell valamilyen indoklás, valamilyen okra való hivatkozás. Ekkor a 'Miért?' kérdésre nem fogadjuk el az "önmagára hivatkozó" indoklást. Az alábbi kérdésre adott választ nem érezzük "teljesnek", elfogadhatónak.
— Miért kéne neked jobban fahéj, mint gyömbér?
— Hát, csak kéne.
— Nekem jobban kéne most fahéj, mint gyömbér.
ezt inkább úgy lehet érteni, hogy nem a preferenciánkat fejeztük ki, hanem "kihirdettük", közöltük a választásunkat, de nem értelmezhetjük úgy, hogy ezzel magyarázatot adtunk volna a 'miért' kérdésre. A választásainknak mindig (de legalábbis az esetek többségében) van indoka, sőt, nagyon sok esetben ezek az indokok pont saját belső $\rel{P}^j$-preferenciáink. A kétféle preferencia közti harmadik különbségről már volt szó: $\rel{P}^j$-hez kell tapasztalat az alternatívákról, $\rel{R}^j$-hez nem feltétlen szükséges. Jennings szerint mondhatjuk, hogy:— Inkább szeretnék a pokolra kerülni, mint a mennyországba.
de – tényleges tapasztalat hiányában – nem mondhatjuk, hogy:— Nekem jobban tetszik a mennyország, mint a pokol.
Jennings ezek után egy formalizálási javaslatot is bemutat az újonnan bevezetett fogalomra, a $\rel{R}^j$-preferenciára. Kiindulásként rögzíti, hogy a $\rel{P}^j$ reláció argumentumai állapotok, az $\rel{R}^j$ reláció argumentumai cselekvések (és csak kényelmi, rövidítési okok miatt használjuk ugyanazokat a jeleket az argumentumok változóinak). Abból indulhatunk ki, hogy ha $\rel{R}^j(m,n)$ igaz, vagyis valaki inkább tenné m-t, mint a n-t, akkor erre mondhatjuk azt is, hogy választania kell az alternatívák közül. Az m és n közti választás az exkluzív diszjunkció (biszubtrakció) műveletével fejezhető ki (☜) vagyis írhatjuk, hogy $m \veebar n$. Az exkluzív diszjunkció képlete: $(m \lor n) \land \lnot (m \land n)$, ahol a formula második tagjával zárjuk ki a két alternatíva együttes fennállását, és ezzel biztosítjuk az alternatívák diszjunktságát. Ezt a formulát viszont – a disztribúciós szabály segítségével – átalakíthatjuk a következő alakra: $(m \land n) \lor (\lnot m \land n)$. Ha ezek után az m és n közötti választás tevékenységét $\#(m,n)$ szimbólummal jelöljük, akkor érvényesnek rá az előző összefüggést.
$\concept{CHOICE}(m,n)\equiv\#(m,n)$
$\#(m,n)\leftrightarrow \#((m \lor n) \land \lnot (m \land n))$
$\#((m \lor n) \land \lnot (m \land n))\equiv\#(m\land\lnot n,\lnot m\land n)$
$\#(m,n)\leftrightarrow\#(m\land\lnot n,\lnot m\land n)$
A választás itt azt jelenti, hogy az ágens m-t választja, n-t viszont nem. A választás mint exkluzív diszjunkció tételezésének van egy fontos következménye: ha a két alternatíva valamelyikének létezése maga után vonja a másik létezését, akkor nem beszélhetünk választásról, hiszen ekkor a két alternatíva nem, hogy nem zárja ki egymást, de az egyik feltételezi a másikat. Jennings szerint a cselekvéseinkre kétféle módon adhatunk magyarázatot: létezik unális (unal), illetve duális (dual) leírás, magyarázat. A $\rel{P}^j$- és $\rel{R}^j$-preferenciák a cselekvéseink duális magyarázatában adhatnak segítséget. Jennings a következő példát adja erre.
| K$_1$ | — Miért csináltad $x$-t?
|
| V$_{11}$ | — Azért, mert x-t akartam csinálni.
|
| V$_{12}$ | — Azért, mert szeretem x-t csinálni.
|
| K$_2$ | — Miért csináltad x-t az y helyett?
|
| V$_{21}$ | — Azért, mert inkább tenném x-t, mint y-t.
|
| V$_{22}$ | — Azért, mert jobban szeretem csinálni x-t, mint y-t.
|
"Az x megtételének akarására vonatkozó indokaim x megtételére vonatkozó indokaim is egyben. Hasonlóan ugyanazok az indokaim arra, hogy miért akarom inkább x-t megtenni y-nal szemben, mint arra, hogy miért teszem meg x-t y-nal szemben. … Vagyis a szeretem x-t tenni és a teszem x-t közti, illetve az akarom x-t tenni és a teszem x-t közti reláció különbözik egymástól. Ugyanolyan különbség létezik aközött, amikor egyfelől azt mondjuk, hogy van P-preferenciánk megtenni x-t y-nal szemben és megtesszük x-t y-nal szemben, illetve amikor másfelől van egy R-preferenciánk megtenni x-t y-nal szemben és megtenni x-t y-nal szemben. A kedveléseink egyrészt indokot, másrészt magyarázatot szolgáltatnak mind az R-preferenciáinkra, mind a cselekvéseinkre." [Jenni] [♦]
Jennings megkülönböztetését jobban meg lehet megérteni, miután elemeztük a választás (☜) valamint az intencionalitás problémakörét, illetve pontosabban elkülönítettük egymástól a vágy és akarat fogalmait (☜) A preferenciákat vizsgálva von Wright felvetett még egy további tipizálási lehetőséget is, amikor elkülönítette azokat helyzeteket, amelyekben van kockázat (risk) azoktól, amelyekben nincs. Még azt is javasolta (igaz, nem indokolja meg, miért), hogy a kockázatmentes (risk-free) preferenciakinyilvánításokat nevezhetnénk tiszta preferenciáknak (pure preferences), míg a kockázatot is magába foglaló preferenciarendezésekre használhatnánk a preferenciális választások (preferential choices) kifejezést. Ha egy ponton módosítunk von Wright korábbi példáján (☜) azt feltételezve, hogy a munkavállalónak úgy kell döntenie a munkahelyén, hogy a fizetésemelést (m) vagy hosszabb éves szabadságot (n) választja inkább a napi munkaidő csökkentéshez (o) képest, hogy az első alternatíva diszjunkciójában (m vagy n) szereplő két összetevő közül csak az egyik teljesülhet, viszont nem előre lehet tudni, hogy melyik. Ha eközben igaz az is, hogy az alternatívák páronkénti összehasonlítás alapján az illető jobbnak tartja a fizetésemelést (m-t) a rövidebb munkaidőnél (o-nál), viszont utóbbit jobbnak ítéli a hosszabb szabadságnál (n-nél), akkor a döntési helyzetbe kockázat "kerül". Ha a munkavállaló az ($m\lor n$) opciót választja, akkor – a döntése után – kiderülhet, hogy a legpreferáltabb állapothoz jut, de az is lehet, hogy a legkevésbé kedvelt alternatívához. Ha viszont a második alternatívát választja, akkor biztosan nem érheti el a legkívánatosabb állapotot, amire pedig valamilyen valószínűséggel lett volna esélye az első alternatíva választása esetén. A példából az is kitűnik, hogy a preferenciális választásokra nem igazak a disztributivitási kritériumok. Ez volt az oka annak, hogy von Wright rögzítette is, hogy esszéjében csak a tiszta preferenciákkal foglalkozik. Ha fel akarjuk venni ezt a megkülönböztetést az ontológiánkba, akkor definiálni kell a kockázat fogalmát, ami alapján már könnyen meg lehet határozni a most bemutatott kétféle preferenciafogalmat is. A kockázatot úgy vehetjük figyelembe, hogy az alternatívákhoz valószínűségeket rendelünk, és a preferenciareláció argumentumaiba ezeket írjuk be, vagyis az m alternatívát az $m|p_m$, az n alternatívát az $n|p_n$ feltételes formulával cseréljük le (ahol $p_m$ és $p_n$ a két alternatívához rendelt valószínűség). A tiszta preferencia és preferenciális választás közti különbséget pedig így fejezhetjük ki formulákkal.$\concept{PURE\_PREFERENCE}\equiv\concept{PREFERENCE}\defi \rel{P}(m|p_m,n|p_n) \land p_m=0\land p_n=0$
tiszta preferencia (hun) – pure preference (eng)
$\concept{PREFERENTIAL\_CHOICE}\equiv\concept{CHOICE}\defi \rel{P}(m|p_m,n|p_n)\land p_m \ne 0\land p_n\ne 0$
preferenciális választás (hun) – preferential choice (eng)
Kockázatmentes helyzetekben a tiszta preferenciáinkat nyilváníthatjuk ki, ezeket tarthatjuk az igazi, külső befolyástól (valószínűségekre alapozott megfontolásoktól) mentes értékkifejeződéseknek. Az intrinzikuskus preferencia kritériumrendszerét erre a típusra dolgozta ki von Wright. A kockázatterhes helyzetekben, amikor a különböző valószínűségekkel ellátott állapotok között kell választanunk, más logika mentén működik az ember.Ceteris paribus preferencia
Az ötödik axiómát von Wright még az amplifikáció elveként vezette be (☜) de később (és mindenhol máshol) ezzel a tulajdonsággal már a ceteris paribus preferenciát írta le (amit aztán az 1972-es tanulmányában már holisztikus preferenciának hívott). A lehetséges terminusok közül végül a ceteris paribus preferencia kifejezés vált elterjedtté, ezt használom én is. Bengt Hansson kritizálta az amplifikáció elvét mondván, hogy ellentmondáshoz vezethet, ha az alternatívák nem függetlenek egymástól. Könnyen szemléltethető mindez, ha feltételezzük, hogy $o=m\land n$. Ezt az egyenlőséget behelyettesítve az amplifikáció elvének formulájába, majd a fölösleges belső konjunkciókat kiiktatva, illetve a belső konjunkciók szimmetriáját kihasználva a következő képletsort kapjuk.
$1)\;\forall m\forall n \forall o(\rel{P}(m,n)\leftrightarrow(\rel{P}(m \land o,n \land o)\land \rel{P}(m \land\lnot o,n \land\lnot o)))$
$2)\;\forall m\forall n \forall o(\rel{P}(m,n)\leftrightarrow(\rel{P}(m \land m\land n,n \land m\land n)\land \rel{P}(m \land\lnot (m\land n),n \land\lnot (m\land n))))$
$3)\; \forall m\forall n \forall o(\rel{P}(m,n)\leftrightarrow(\rel{P}(m \land n,n \land m)\land \rel{P}(m \land\lnot (m\land n),n \land\lnot (m\land n))))$
$4)\; \forall m\forall n \forall o(\rel{P}(m,n)\leftrightarrow(\rel{P}(m \land n,m \land n)\land \rel{P}(m \land\lnot (m\land n),n \land\lnot (m\land n))))$
A negyedik sorban már látszik az ellentmondás, hiszen a bikondicionális jobb oldalán álló konjunkció első tagja ($\rel{P}(m \land n,m \land n)$) ellentmondásban van von Wright \rel{P}-relációjával, ami – lévén szigorú preferenciarendezés – aszimmetrikus. Ezt persze korrigálni lehet a korábban már többször alkalmazott ellentmondásbiztos klauzula beépítésével az elv formulájába. Ez tehát "kezelhető" problémát jelent. És nem is lényeges ponton "támadja" a ceteris paribus preferencia fogalmát. Von Wright számára nem ezért volt fontos ez a fogalom. Amikor preferenciáról beszélünk, akkor két állapotot hasonlítunk össze. Feltehető a kérdés, hogy amikor így döntünk, akkor vajon figyelembe vesszünk-e más állapotokat, illetve állapotváltozásokat, és ha igen, akkor mennyit? Mi van akkor, ha figyelünk arra is, hogy nem csak két, de több állapot is fennállhat akkor, mikor éppen azt a két állapotot hasonlítjuk össze, és mi van akkor, ha nemcsak az éppen összehasonlított állapotok változhatnak, hanem bármi más is. Akkor érthetjük meg, hogy miért is fontos ez a kérdés, ha von Wright harmadik axiómájára gondolunk, miszerint preferálni m-t n-nel szemben ekvivalens azzal, hogy a jelen helyzethez képest preferáljuk azt a változást, ami az $(m\land\lnot n)$ helyzetbe visz minket ahhoz a változáshoz képest, ami az $(\lnot m\land n)$ helyzetet eredményezi. Ebben az interpretációban már sokkal érthetőbb, miért lehet feltenni azt a kérdést, hogy ilyen esetekben miért nem veszünk figyelembe más változásokat, más helyzeteket is. A kérdésre válaszul von Wright háromféle lehetőséget különít el egymástól: az abszolút, a feltétel-nélküli és feltételes preferencia kinyilvánításának helyzetét. Amikor az egyén az $(m\land\lnot n)$ állapotot eredményező változást nemcsak a $(\lnot m\land n)$, de bármely más állapotot eredményező változáshoz képest is preferálja, akkor abszolút preferenciáról (absolute preference) beszélhetünk. Ilyen esetekben ha egy világállapot tartalmazza a $(\lnot m\land n)$ állapotot, akkor azt ez az egyén mindenképpen jobban tartja az összes többi világállapotnál, amelyben $(\lnot m\land n)$ is benne van. Az ilyen abszolút preferenciából azonban egy ember (egy adott pillanatban) csak eggyel rendelkezhet (ezt a tézist von Wright röviden le is vezeti, amit itt nem mutatok be), ezért ezt a preferenciatípust von Wright elhanyagolhatónak véli (mivel a gyakorlatban érdektelen). A feltételes preferencia (conditional preference) fogalmát úgy értelmezi von Wright, hogy ilyen esetekben két állapot összehasonlítása függ egy harmadik állapottól. Azt a példát adja erre, hogy ha valakinek pénzre van szüksége és el kell adnia egy ruhadarabját, akkor három ruhadarabot (trikót, cipőt és nadrágot) feltételezve másként értékelheti azt a kérdést, hogy melyiket adja el a trikó (m) és a cipő (n) közül attól függően, hogy mit gondol a nadrág (o) eladásáról. Ha nem kell (nem akarja) eladni a nadrágot, akkor preferálja a cípőt a trikóval szemben (mert az "megy" a nadrághoz), vagyis az utóbbit fogja eladni. Ha viszont el kell (el akarja) adni a nadrágot (mert, mondjuk, kinőtte), akkor már inkább a trikó megtartását választja a cipővel szemben (mert nadrág nélkül úgysem használhatná). A feltétlen vagy feltétel-nélküli preferenciáról (unconditional preference) akkor beszélhetünk, amikor feltételezhetjük, hogy a világ nem változik más állapotait tekintve, tehát csak az m és n állapotokat érintő változások történnek. E helyzet leírására szokták használni a ceteris paribus preferencia kifejezést. [♦] A von wrighti preferencialogika a feltétel-nélküli, ceteris paribus preferenciákról szól. A feltétel-nélküliség mozzanatát von Wright az ötödik axiómájával definiálta. Ez a tétel egy elsőrendű logikai szintaxison alapuló formula igazságát tételezi. Azóta kiderült, hogy a ceteris paribus elvet igazából a modális logika segítségével lehet jól megragadni. Von Wright megoldási javaslata után sokáig az volt a kérdés, mi lehet a jó megoldás erre. Sven Ove Hansson már 1995-ben tett egy javaslatot a formalizálásra [SvenO] amit aztán egy 2001-es cikkében kissé módosított [SvenO] de a széles körben elfogadott megoldást mások dolgozták ki (☜)
Preferencia és tranzitivitás
A tranzitivitás feltételét sokan vitatják arra hivatkozva, hogy a tényleges társadalmi gyakorlatban sok olyan példát találhatunk, amikor nem érvényesül ez a tulajdonság. Von Wright is tudatában volt a tranzitivitással szembeni kételyeknek, de azt válaszolta, hogy a tranzitivitás ellenében felhozott ellenpéldák szinte mindig az extrinzikus preferenciákra vonatkoznak, amikor valami hatására időközben megváltozik valakinek a preferenciarendezése (hiszen, mondja von Wright, a tranzitivitás mérése időbeli folyamat, ami alatt változhat az extrinzikus preferencia). Szerinte az intrinzikus preferenciákra fenntartható a tranzitivitás kritériuma. Még ha sokan vannak, akik túl erősnek tartják, ezért nem fogadják el a preferencia tranzitivitási feltételét, a tranzitivitás tulajdonságának fontosságát senki sem tagadja. Nélkülözhetetlenségét jelzi az a tény is, hogy sokféle módon próbáltak gyöngíteni a tranzitivitás kritériumán, és új tranzitivitás-közeli fogalmakat vezettek be. Ilyenek előfordultak a relációtulajdonságok között is (☜) emlékezzünk csak például a kvázi-tranzitivitás vagy az aciklusosság fogalmára. A relációtulajdonságokkal való minősítésen túl úgy nyerhetünk további tranzitivitás-közeli fogalmakat, hogy több relációt vonunk be a definíciókba. Ilyeneket definiáltuk a relációelméleti fejezetben, például az IP- vagy a PI-tranzitivitás fogalmait (☜) Mivel akkor még nem vezettük be a különböző preferenciarelációkat, így egyetlen relációra támaszkodva kellett megadnunk a definíciókat. Most már egyszerűsíthetünk a korábbi formulákon, ha az $\rel{R}$ gyenge preferencia fogalmából képzett $\rel{P}$ szigorú preferencia, illetve az $\rel{I}$ indifferencia relációk meghatározásait is figyelembe vesszük.$\concept{PP-TRANSITIVE}(\rel{R}(m,n))\defi \forall m \forall n \forall o((\rel{P}(m,n) \land \rel{P}(n,o)) \to \rel{P}(m,o))$
PP-tranzitív (hun) – PP-transitive (eng)
$\concept{IP-TRANSITIVE}(\rel{R}(m,n))\defi \forall m \forall n \forall o((\rel{I}(m,n) \land \rel{P}(n,o)) \to \rel{P}(m,o))$
IP-tranzitív (hun) – IP-transitive (eng)
$\concept{PI-TRANSITIVE}(\rel{R}(m,n))\defi \forall m \forall n \forall o((\rel{P}(m,n) \land \rel{I}(n,o)) \to \rel{P}(m,o))$
PI-tranzitív (hun) – PI-transitive (eng)
$\concept{II-TRANSITIVE}(\rel{R}(m,n))\defi \forall m \forall n \forall o((\rel{I}(m,n) \land \rel{I}(n,o)) \to \rel{I}(m,o))$
II-tranzitív (hun) – II-transitive (eng)
A későbbiekben még használjuk ezeket a tranzitivitási tulajdonságokat, illetve a különböző tézisekben, levezetésekben nem egyszer lehet hivatkozni azokra az összefüggésekre, amelyek a tranzitivitás fogalomkörébe tartozó tulajdonságok között állapíthatók meg. Fel lehet tenni itt a kérdést, miért van szükség ilyen sokféle fogalomra a tranzitivitás fogalombokrán belül. Azért, mert a racionális emberi cselekvések magyarázatában igyekszünk kizárni az egymás után kimondott preferenciaállítások sorából a ciklikusság megjelenését. De miért is baj a ciklikusság? Erre a kérdésre Amos Tversky pénznyelő (money-pump) példájával szokás válaszolni. Ha nem követelnénk meg a tranzitivitást, akkor a viselkedésünket ugyanúgy irracionálisnak lehetne minősíteni, mint Tversky példaemberének cselekvését."A tranzitivitás a racionális visekedés egyik alapvető és talán legszigorúbb elve. Mondhatjuk azt is, hogy aki megsérti a tranzitivitás elvét, az voltaképpen 'pénznyelőként' működik. Tegyük fel, hogy valaki preferálja y-t x-hez, z-t y-hoz, valamint x-t z-hez képest. Ekkor megalapozott lehet az a feltételezésünk, hogy az illető hajlandó fizetni azért, hogy kicserélhesse először x-t y-ra, aztán y-t z-re, végül z-t x-re. Ám ha így tesz, a végére ugyanoda jut, ahonnan indult, csak épp kevesebb lesz a pénze." [Tvers]
A preferenciarelációkat (szigorú rendezés, gyenge rendezés, indifferencia) egymás után többször is lehet alkalmazni, vagyis sorba lehet őket kötni. Ilyen esetekben egyszerűsíthetünk a jelölésen, ha az egymást követő diadikus viszonyokat lineaárisan "összekötjük" (a formulában a közömbösségi reláció '$\shortparallel$' szimbólumát használjuk (☜)$\rel{P}(m,n)\land \rel{P}(n,o)\land\rel{I}(o,p)\equiv \rel{PPI} \equiv (m>n) \land (n>o) \land (o\;\shortparallel p)\equiv m>n>o \;\shortparallel p$
Bármennyire is fontosnak és szükségesnek érezzük a tranzitivitást mind a preferencia, mind a racionális viselkedés meghatározásához, az intranzitivitás, a ciklikusság gyakran tetten érhető a cselekvéseinkben. Sven Ove Hansson szerint négyféle tipikus tranzitivitási kör létezik, és az elemzésekben felhozott legtöbb példa ezek valamelyikébe tartozik [SvenO] A továbblépés előtt érdemes bizonyos jelölési konvenciókat bevezetni.| $\rel{I}^n\rel{P}-cycle$ | egymás után $n$-szer $\rel{I}$-, majd egy $\rel{P}$-reláció követi egymást $(n\geq 2)$ | |||||||||||||
| $\rel{IPIP}-cycle $ | egy $\rel{I}$-, egy $\rel{P}$-, $\rel{I}$-, $\rel{P}$-reláció követi egymást | |||||||||||||
| $\rel{IPP}-cycle $ | egy $\rel{I}$-, majd két $\rel{P}$-reláció követi egymást | |||||||||||||
| $\rel{P}^n-cycle$ | egymás után $n$-szer $\rel{P}$-reláció követi egymást $(n\geq 3)$ | |||||||||||||
| $m$ | utazás Kaliforniába | |||||||||||||
| $n$ | utazás Floridába | |||||||||||||
| $o$ | utazás Kaliforniába + egy alma | |||||||||||||
| $m$ | utazás Kaliforniába | |||||||||||||
| $n$ | utazás Floridába | |||||||||||||
| $o$ | utazás Floridába + egy alma | |||||||||||||
| $p$ | utazás Kaliforniába + egy alma | |||||||||||||
$\concept{SEMIORDER}\defi$
$1)\;\;\forall m \forall n(\rel{P}(m,n)\veebar\rel{P}(n,m)\veebar\rel{I}(m,n))$
$2)\;\;\forall m(\rel{I}(m,m))$
$$3)\;\;\forall m \forall n \forall o \forall p((\rel{P}(m,n)\land\rel{I}(n,o)\land\rel{P}(o,p))\to\rel{P}(m,p))$
$4)\;\;\forall m \forall n \forall o \forall p((\rel{P}(m,n)\land\rel{P}(n,o)\land\rel{I}(n,p))\to\lnot(\rel{I}(m,p)\land\rel{I}(o,p)))$
szemirendezés (hun) – semiorder (eng)
Tversky megjegyezte, hogy szemirendezés a lexikografikus rendezésnek egyik típusát is jelenti egyben. Észre kell azonban vennünk, hogy ez a fogalom egy nagyon fontos ponton eltér az eddig rendezési fogalmainktól. Itt ugyanis nem egy, hanem két rendezési fogalomról (egy preferencia- és egy indifferenciarelációról) van szó, ami az "egyszerű" rendezésekhez képest egy eddig nem látott problémához vezet: ahhoz, hogy a kétféle rendezési relációtól végleges (valamiféle együttes) eredményt várhassunk el, az kell, hogy a "belső" relációk között is megállapítsunk valamilyen viszonyrendszert. Csak ennek létezésekor (és ennek ismeretében) lehetséges ugyanis az egyesített végeredmény elérése. A probléma kezelése, megoldása azonban már kivezet minket a preferencialogika szűkebb értelemben vett területéről, ezért itt most nem foglalkozom vele. Később természetesen még visszatérek erre a kérdésre (☜)Ceteris paribus preferencia modális logikai alapon
Korábban már bevezettem a ceteris paribus preferencia fogalmát (☜) és jeleztem azt is, hogy a fogalom formális leírását modális logikai alapon lehet jól megoldani. Most érkeztünk el arra a pontra, amikor felvázolhatom, hogyan lehet ezt a formalizálást elvégezni. Kiindulásként idézzük fel az amplifikáció elvének formuláját, amit von Wright összekapcsolt a ceteris paribus preferenciával (a formulából itt elhagyjuk a kvantorokat).$\rel{P}(m,n)\leftrightarrow(\rel{P}(m \land o,n \land o)\land \rel{P}(m \land\lnot o,n \land\lnot o))$
A ceteris paribus elv azt akarja megragadni, hogy a preferenciáinkat úgy fejezzük ki két állapot között, hogy közben minden más állapotot változatlannak ítélünk meg. Először érdemes röviden értelmezni, mit is jelent ez a kijelentés. Az összehasonlítandó állapotok összességét nevezhetjük a tárgyalási univerzumnak (universe of discourse). Ebben a modellben a ceteris paribus elvet úgy kell értelmeznünk, hogy ha két állapotot (m-t és n-t) vetünk össze, akkor minden o állapotot, alternatívát a tárgyalási univerzumban, amelynek nincs direkt relevanciája az értékelés során, konstansnak tekintünk az összehasonlítási folyamat egészében. Vegyünk egy példát! Tegyük fel, hogy az esőköpenyt (r) preferáljuk az esernyővel ($u$) szemben $\rel{P}(u,r)$ miközben harmadik potenciális alternatívaként ott van az az állapot is, hogy csizmát viselünk (b). Ekkor a tényleges, aktuális preferenciánkat így írhatjuk le: $\rel{P}(r \land \lnot b,u \land b)$. Megváltozna az értékelésünk, ha elvesztenénk a csizmánkat, mert ez a tény átfordítaná a preferenciánkat, és az esőkabátot preferálnánk az esernyővel szemben, de az amplifikációs szabály elfogadása kizárja ezt a lehetőséget. A ceteris paribus elv érvényessége azt jelenti, hogy a csizma (r alternatíva) léte (vagy nem léte) nem befolyásolhatja a döntést, tehát mindvégig konstansnak kell tartanunk a hatását, és ezért el kell tekintenünk tőle. A ceteris paribus elv a kontextualis érvényességet, a preferenciák viszonylagosságát fejezi ki. Fontos előzményként kell tekintenünk Jon Doyle és Michael Wellman cikkére, amelyben a szerzők először bontották fel két összetevőre a ceteris paribus preferenciák reprezentálásának feladatát [Doyle] Doyle és Wellman abból a praktikus szempontból fontos kérdésre kereste a választ, hogy miként lehetne a propozíciók között összehasonlításokat (és ezáltal preferenciarendezéseket) tenni. Doyle-ék számára azért fontos ez a kérdés, mert von Wright állapotok közti preferenciákról beszélt, amiket individuális propozíciókkal mindig le lehetett írni, de amikor a mérnökök a számítógépes döntéstámogató rendszerek fejlesztése során a céltételezésekben, eszközkiválasztásokban megbúvó preferenciákat is modellezni akarták, akkor hamar kiderült, hogy nem járható út az, amikor a preferenciákat az individuumok szintjén adják meg a rendszer számára, mert végtelen sok adat összegyűjtésére, betáplálására és számítására lenne szükség. Ehelyett kínálta magát az a lehetőség, hogy az individuális szintű adatok helyett általánosabb szintű adatokat kezeljenek, de itt újfajta gondok jelentkeztek. [♦] Az individuumok összehasonlítása "egyszerű". Ha Béla magasabb, mint Kati, vagy Hans jobban szereti a magasabb fizetést az alacsonynál, akkor erre könnyű képleteket, számítógépes programokat írni. De mi van akkor, ha individuumok valamilyen osztályát kell összehasonlítani. Például egy ruházati cég számára fontos lehet az olyan megállapítás, hogy a dánok magasabbak és soványabbak, mint a szicíliaiak, mert ennek ismeretében más méretű ruhákkal megy be a két piacra. Amikor ilyenfajta döntéseket kell hozzunk, akkor persze mindig találhatunk kivételeket, de ezt tudva is törekszünk arra, hogy ne individuumokra, hanem individuumok egész osztályára tudjunk összehasonlító állításokat tenni. Vannak tehát az individuumok (ahol könnyen tudunk összehasonlításokat tenni), és vannak az individuumok osztályát leíró propozíciók, ahol – egyelőre – még nem megoldott az összehasonlítás. Első lépésként megpróbálhatjuk az individuumokra vonatkozó összehasonlítást (preferenciarendezést) az individuumok valamely osztályára vonatkozó összehasonlítássá alakítani a sima felemelés (simple lifting) módszerével. Tegyük fel, hogy az alábbi egyedeink vannak egy adott $\Omega$ halmazban: $m, n \in \Omega $, és ezek a következő osztályokba tartoznak: $m \in \phi, n \in \psi $. Ekkor nyilván igaz, hogy: $\phi, \psi \subseteq \Omega$. Ekkor az egyedek közti a már jólismert preferenciarendezési műveleteket értelmezhetjük: a $\succeq$ legalább olyan jó, a $\succ$ szigorúan jobb és az $\sim$ indifferens relációt. Ezek alapján – a sima felemelés módszerével – definiálhatjuk az osztályok (propozíciók) közti rendezéseket is.
$1)\;\; \phi \succeq \psi \defi \forall m \in \phi \forall n \in \psi (m \succeq n)$
$2)\;\; \phi \succ \psi \defi \forall m \in \phi \forall n \in \psi (m \succ n)$
$3)\;\; \phi \sim \psi \defi \forall m \in \phi \forall n \in \psi (m \sim n)$
Ezzel a megoldással azonban komoly gondok adódnak, amit akkor érthetünk meg igazán, ha egy konkrét példán keresztül szembesülünk az elképzelés nem kívánt következményeivel. Ehhez először definiálnunk kell pár további feltételt. Elsőként rögzítenünk kell azt, hogy az összehasonlítandó szempontokat (propozíciókat) logikailag függetlennek kell tartani egymástól. Ha ezt nem követelnénk meg, akkor az összehasonlítások során logikai ellentmondásokhoz juthatnánk (erről már volt szó korábban). A logikai függetlenséghez az szükséges, hogy a propozíciók és komplementereik összes lehetséges metszetében legyen előfordulás. A dolgok szemléltetéséhez elégséges a szemifüggetlenség – némileg gyengébb – fogalma is, amikor nem kell az összes lehetséges kombinációra megkövetelni a nem-ürességet.
$\forall i \forall j(\phi_i\cap \phi_j\ne\emptyset \;\land\; \phi_i\cap \overline{\phi}_j\ne\emptyset \;\land\; \overline{\phi}_i\cap \phi_j\ne\emptyset \;\land\; \overline{\phi}_i\cap \overline{\phi}_j\ne\emptyset)$
logikai függetlenség (hun) – logical independence (eng)
$\forall i \forall j(\phi_i\cap \overline{\phi}_j\ne\emptyset \;\land\; \overline{\phi}_i\cap \phi_j\ne\emptyset)$
logikai szemifüggetlenség (hun) – logical semi-independence (eng)
A logikai szemifüggetlenség alapján definiálhatunk háromféle 'legnagyobb rendezés' fogalmat mint a 'legnagyobb' minősítés három meghatározott fokozatát. Ezeket a következő formulákkal fejezhetjük ki.$\forall i((\phi_i \succeq \overline{\phi}_i \land \forall k\forall l(\phi_k\overline{\phi}_l\ne \emptyset)) \to \forall m \in \phi_i \forall n \in \overline{\phi}_i (m \succeq n))$
maximálisan legnagyobb (hun) – maximal greatness (eng)
$\exists i(\phi_i \succeq \overline{\phi}_i \to \forall m \in \phi_i \forall n \in \overline{\phi}_i (m \succeq n))$
közepesen legnagyobb (hun) – intermediate greatness (eng)
$\exists i\exists j(\phi_i \succeq \overline{\phi}_i \to \forall m \in \phi_i \forall n \in \overline{\phi}_j (m \sim n))$
minimálisan legnagyobb (hun) – minimal greatness (eng)
Jobban megérthetjük mind a fenti definíciókat, mind a bemutatni kívánt problémát, ha megvizsgálunk egy konkrét esetet. Doyle és Wellman a következő példát hozta. Vegyünk két szempont, a fizetést és a napi munkaidő hosszát, és ezek alapján ítéljük meg a választható munkahelyeket. Külön-külön mondhatjuk, hogy a magas fizetés jobb, mint az alacsony, illetve a rövidebb munkaidő jobb, mint a hosszabb. Ezek alapján egyértelmű összehasonlításokat tudunk tenni. De gondba kerülünk, ha a két szempontot egyszerre akarjuk figyelembe venni. Egy ábra segítségével megvilágíthatjuk, miért. Mivel egy szemponton belül kizáró vagylagos választható lehetőségek vannak, az alternatívák így egymás ellentettjeinek, komplementereinek számítanak. Ezt figyelembe véve jelöljük a választási lehetőségeket a következő módon.| $\phi$ | – magasabb fizetés | |||||||||||||
| $\overline{\phi}$ | – alacsonyabb fizetés | |||||||||||||
| $\psi$ | – rövidebb munkaidő | |||||||||||||
| $\overline{\psi}$ | – hosszabb munkaidő | |||||||||||||
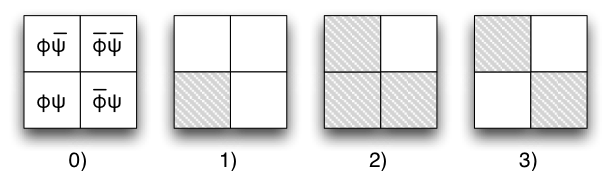
A választható konkrét munkahelyeket mindig besorolhatjuk az ábra 0) jelű négyzetének valamelyik negyedébe, az 1)-2)-3) jelű négyzetek pedig azt mutatják, hogy a korábban definiált három rendezési reláció melyik negyede(ke)t jelöli ki a legjobbnak. Az 1) négyzet jelöli a maximálisan legnagyobb rendezés eredményét, amikor azokat a konkrét egyedeket soroljuk ide, amelyek mindkét szempont szerint jobbak voltak. Ezek azok a munkahelyek, amelyek magas fizetést adnak és rövid munkaidejűek (vagyis mindkét szempont szerint jobbak). A 2) négyzet a közepesen legnagyobb rendezésnek felel meg. Ez az összehasonlítás azokat az individuumokat minősíti jobbnak, amelyek legalább egy szempont szerint jobbak a többinél. Ilyenek lesznek mindazok a munkahelyek, amelyek vagy magasabb fizetést, vagy rövidebb munkaidőt kínálnak, vagy mindkettőt egyszerre nyújtják. Ez jóval gyengébb feltétel az előzőhöz képest, így ennek a kritériumnak sokkal több munkahely képes megfelelni. Az ábra 3) jelű négyzete mutatja, hogy milyen eredményt adna vissza a minimálisan legnagyobb rendezés. Ekkor a két egyenlően legnagyobb állapotot jelent az, amikor az egyik szempont szerint jobbak, a másik szerint rosszabbak az alternatívák, illetve fordítva. Ezzel a rendezési hármas javaslattal az a legnagyobb probléma, hogy nem ad módot mindenféle más összehasonlításra. Nem kerülhetünk olyan helyzetbe például, amikor a magasabb fizetésű és hosszabb munkaidejű munkahelyet preferálnánk az alacsonyabb fizetéssel és rövidebb munkaidővel szemben. Márpedig olykor kívánatos lenne. Például akkor, amikor a ceteris paribus elvet szeretnénk modellezni. Valahogyan gyöngíteni kell a feltételeken, hogy be tudjuk vezetni a ceteris paribus elvet. Doyle és Wellman újítása az volt ezen a ponton, hogy bevezették a kontextuális összehasonlítás (contextual comparison) fogalmát, amit elvezethet minket a ceteris paribus összehasonlítás lehetőségéhez. Ha azt mondjuk, hogy két individuum 'ugyanaz, miközben minden más változatlan' (same, other things equal), akkor ez két lépésben definiálható. Elsőként biztosítani kell azt, hogy valamik ugyanazok, amit az individuumok közötti ekvivalenciával ragadhatunk meg, majd azt kell valahogy megfogni, hogy minden más változatlan. Ehhez kell a kontextuális ekvivalencia fogalma, amire már "ráülhet" a ceteris paribus összehasonlítás (comparison ceteris paribus). A kontextuális ekvivalenciát Doyle-ék az alábbi módon definiálták.
$\concept{CONTEXTUAL\_EQUIVALENCE}(m,n)\equiv m \cequiv n \;\conmod{mod} \;\phi,\psi, \dots \defi \mathcal{P}(\mathcal{P}(\Omega)) \mapsto \epsilon(\Omega)$
kontextuális ekvivalencia (hun) – contextual equivalence (eng)
Az individuumok közti ekvivalenciarelációk segítségével ragadhatjuk meg a propozíciókat, hiszen a propozíciók (vagy azok komplementerei) alá sorolható egyedek mind ekvivalensek egymással ebben a minőségükben. A kontextuális ekvivalencia fogalmának segítségével már definiálni lehet a gyengén nagyobb ceteris paribus rendezési relációt.$\concept{WEAKLY\_GREATER\_CP}(\phi,\psi)\equiv\phi\trianglerighteq\psi\defi \forall m\in\phi\overline{\psi}\forall n\in\overline{\phi}\psi(m\succeq n \land (m \cequiv n \;\conmod{mod} \;\psi\overline{\psi},\overline{\phi}\psi))$
gyengén nagyobb ceteris paribus (hun) – weakly greater ceteris paribus (eng) – gyengén jobb ceteris paribus (hun)
Miért is érdekes ez? A definíció azokat az individuumokat hasonlítja össze, amelyekre fennáll, hogy $\phi\overline{\psi}$-be, illetve a $\overline{\phi}\psi$-be tartoznak, nem pedig azokat, amelyekre az lenne igaz, hogy a $\phi$-be, illetve a $\psi$-be tartoznának. Azért értelmes ez így (és nem értelmes másként), mert az az összehasonlítás, amely során mindkét individuum benne lenne $\phi$-ben, nem tudna köztük releváns módon különbséget tenni csak az alapján, hogy kielégítik-e $\psi$-t (hiszen $\phi$-t mindketten kielégítik). Mivel fordítva is hasonlót mondhatnánk, vagyis ha az összehasonlítandó egyedek benne lennének a $\psi$-ben, akkor azokat csak a $\phi$ alapján lehetne összehasonlítani. Ezért csak a definícióban alkalmazott összehasonlítási mód alapján lehetséges értelmesen keresni és megállapítani két propozíció viszonyát. További két összehasonlítási operátort is definiálhatunk.$\concept{STRICTLY\_GREATER\_CP}(\phi,\psi)\equiv\phi \vartriangleright \psi \defi \phi\trianglerighteq\psi\land \lnot(\psi\trianglerighteq\phi)$
erősen nagyobb ceteris paribus (hun) – strictly greater ceteris paribus (eng) – szigorúan jobb ceteris paribus (hun)
$\concept{EQUALLY\_GREAT\_CP}(\phi,\psi)\equiv\phi \triangleq \psi \defi \phi\trianglerighteq\psi\land \psi\trianglerighteq\phi$
egyenlően nagy ceteris paribus (hun) – equally great ceteris paribus (eng) – ugyanolyan jó ceteris paribus (hun)
Az értelmezéshez nézzünk meg egy újabb példát: hasonlítsuk össze az embereket a testmagasságuk, illetve testsúlyuk alapján. Soroljuk be úgy az embereket, hogy mindkét dimenzióban legyen három-három fokozatunk. A tulajdonságfokozatokat, illetve ezek komplementerét mind egy-egy proporzíciónak tarthatjuk, és az alábbi módon jelölhetjük.| $m$ = magas | $\overline{m}$ = közepes + alacsony | $s$ = sovány | $\overline{s}$ = normál + túlsúlyos |
| $k$ = közepes | $\overline{k}$ = magas + alacsony | $n$ = normál | $\overline{n}$ = sovány + túlsúlyos |
| $a$ = alacsony | $\overline{a}$ = magas + közepes | $t$ = túlsúlyos | $\overline{t}$ = sovány + normál |
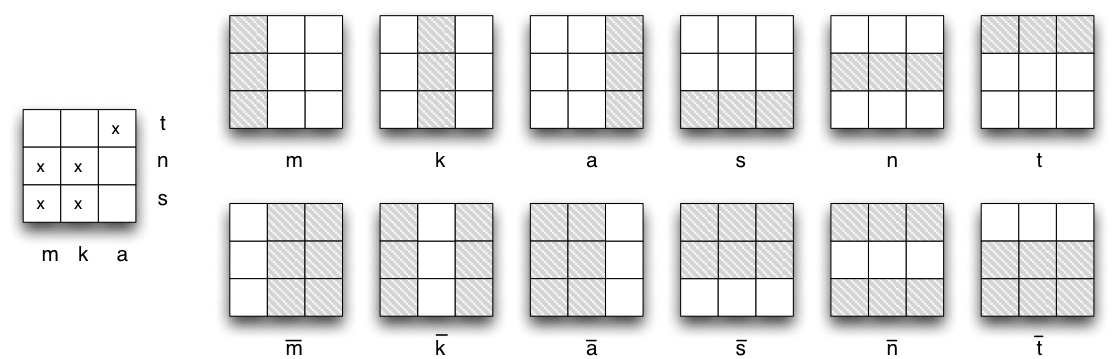
A kérdés, hogy mit mondhatunk a ceteris paribus preferenciákról ebben az esetben. Nos, két állítást tehetünk. Mondhatjuk, hogy egyfelől a magas + sovány gyengén jobb ceteris paribus a magas + normál súlyúhoz képest, másfelől a közepes + sovány gyengén jobb ceteris paribus a közepes + normál súlyúhoz képest, vagyis: $m \land s \succeq m \land n$, illetve $k \land s \succeq k \land n$. Johan van Benthem, Patrick Girard és Olivier Roy szerint a feltétel-nélküliséget modális logikai alapon kell inkább megragadni, ezért kidolgozták a ceteris paribus preferencia $\mathscr{L}_\mathcal{P}$ modális nyelvét és modeljét [Johan] Benthemék tanulmánya rövid idő alatt komoly szakmai elismeréseket szerzett. Sokan megkerülhetetlennek minősítették a cikket – megédemelten. A tanulmány gondolatmenetét azonban nem mutatom be itt, mert egyfelől túl hosszú lenne, másfelől nagyon komoly modális logikai felkészültség és tapasztalat szükséges hozzá.
Meghyn Bienvenu, Jér\^{o}me Lang és Nic Wilson kidolgoztak egy olyan általános modális nyelvet és modellt a preferenciára, amely a filozófusok által kidolgozott preferencialogikákat, és mesterséges intelligencia világán belül kifejlesztett preferenciareprezentációs nyelveket egyaránt képes integrálni [Bienv] Ennek – más egyéb okok mellett – azért érezték szükségét, mert figyelemmel akartak lenni az adott nyelven történő gépi következtetések számításigényeire is. A preferencia általános fogalmára nézve különösen igaz, de még az intrinzikus preferenciára vonatkoztatva is kijelenthető, hogy a preferenciáink nem statikusak. Az extrinzikus preferencia együtt változhat azzal, ahogy valamilyen hitünk, ismeretünk megváltozik a világról. Ez a hatás az intrinzikus preferencia esetében is jelentkezhet, bár nyilván lassabban, kevésbé reflektált módon. De a preferenciáink másfajta külső hatásnak is ki vannak téve. Kaphatunk parancsokat, megfogalmazhatnak morális elvárásokat velünk szemben, új információhoz juthatunk, új összefüggéseket ismerhetünk fel, javaslatokat, tanácsokat adhatnak nekünk, melyek eredményeként változhatnak a világra vonatkozó értékeléseink. Johan van Benthem és Fenrong Liu cikke azt elemzi [Johan] hogy a preferenciáink hogyan változnak a javaslatok (suggestion), parancsok (order) hatására miközben különbséget tesznek ulyan fogalmak között mint a frissítés (update) és szintemelés (upgrade) között. Fenrong Liu 2011-ben könyvet jelentetett meg a preferenciák változásairól, dinamikájáról [Fenro]
Deontikus logika
A deontikus logika (vagy imperatív logika) az előírások, kötelezések, tiltások, megengedések formalizálásával foglalkozik. Több szempontból is a legfontosabb logikai diszciplinának minősíthető a cselekvéselmélet számára. Ennek ellenére nem célom bemutatni a deontikus logika kialakulásának, fejlődésének történetét, és nem akarok túlzottan elmélyülni a terület legfontosabb kérdéseiben sem. A témáról szóló könyvek, tanulmányok közül íme egy elfogult és teljesnek messze nem mondható lista: [AlfRo] [Georg] [Lemmo] [AlanR] [Bengt] [Bengt] [Brian] [Brian] [StigK] [Seger] [makin] magyarul olvasható Solt Kornél munkája [SoltK] A cselekvéselmélet számára azért a deontikus logika a leginkább használható, mert a deontikus logikai előírások, modalitások mindig valamilyen cselekvésre vonatkoznak, tehát a cselekvéselmélet központi fogalma, a cselekvés van a deontikus logika fókuszában is. A modális logika különböző kalkulusait meghatározó sémák közül a (D) séma az (☜) amit a deontikus logikához kapcsolhatunk. A deontikus logikában a két modális operátor, a szükségszerű és a lehetséges átértelmezhető úgy, hogy kötelező, illetve megengedett legyen a jelentésük. Ekkor a (D) sémát úgy lehet interpretálni, hogy 'ha valami kötelező, akkor az megengedett is egyben'. A deontikus logika mint a kötelezések logikája "arról szól", hogy mit tudunk mondani a jövőről, pontosabban – a jövőre vonatkozó – kötelezések és megengedések világáról. Minden kötelezés, tiltás, megengedés a jövőre irányul, hiszen az ilyen helyzetek ágensei (vagy legalábbis egy részük) azzal a várakozással fordul az előírások felé, hogy azok a jövőben teljesülni fognak. Ez a jövőre vonatkozás adja a deontikus logika egyik specialitását, hiszen ez azt jelenti, hogy ez a logika nem tényekkel foglalkozik. Ettől még sok minden fontos felismerést, tudást köszönhetünk neki, de azt a "hiányosságát" mindenképpen rögzíteni érdemes, miszerint ez a diszciplina nem tud semmi értelmeset mondani arról, hogy mikor, miért valósulnak meg azok a cselekvések, amelyekre az előírások irányulnak. [♦]Deontikus operátorok
A deontikus logika első elméletében von Wright négy deontikus operátorról írt [Georg] és az utána következő szerzők is kitartottak amellett, hogy a deontikus operátorok a logikai négyszögre "húzhatók rá". Persze, ebben a diskurzusban is "felbukkantak" ugyanazok a problémák, amelyek a logikai négyszög más területeken való alkalmazásakor jelentkeztek (☜) A kötelező és a tiltott univerzális kategóriákkal nem nagyon voltak problémák, de bizonytalanság, pontatlan fogalmi határok jellemezték a partikuláris kategóriákat. A megengedett deontikus modalitás értelmezhető volt mind az állító, mind a tagadó partikuláris kategóriákra, bár intuitívabbnak tűnt az állító jellegű használata. Olykor "nehézséget okozott" a négyszög (O)-sarokjának megnevezése, illetve pontos értelmezése is. Fontosságuk miatt sok nyelvi forma termelődött ki a kategóriák jelölésére. Íme egy – biztos nem teljes – lista magyarul.| kötelező | megparancsolt, kellő, támogatott, obligát, ajánlott, muszáj, szükséges, nem mellőzhető, nem lehet nem megtenni | |||||||||||||
| tilos | tiltott, nem lehet, nem lehetséges, nem szabad, nem megengedett, megengedhetetlen, tűrhetetlen, nem tűrt, elfogadhatatlan, kötelező tartózkodni | |||||||||||||
| megengedett | szabad, lehet, lehetséges, jogos, nem tilos, nem tiltott, tűrt, elfogadott, tolerált | |||||||||||||
| mellőzhető | szabad, lehet, lehetséges, jogos, nem kötelező, elhagyható, elmulasztható, eltekinthető, eltekintett, felmentett, tolerált | |||||||||||||
| obligatory | commanded, duty, compulsory, required | |||||||||||||
| forbidden | impermissible, banned, prohibited, prohibition, disallowed | |||||||||||||
| permitted | permissible, allowed, right, free, claim | |||||||||||||
| omissible | non-obligatory, no-duty, duty-free, gratuitous, exemption | |||||||||||||
(1)
Ha valaki egy közúti baleset helyszínére ér, megengedett számára, hogy segítsen.
(2)
Ha valaki megszerezte a vezetői engedélyét, megengedett számára, hogy gépjárművet vezessen.
(3) Megengedett, hogy ne szavazzon valaki a parlamenti választásokon.
Ez a megengedés azt fejezi ki, hogy valami (itt: a szavazás cselekedete) nem kötelező, ami viszont logikailag "megengedi" azt az értelmezést, hogy ez a valami, vagyis a szavazás akár tilos is lehet. Van tehát három példamondatunk, amelyekben három – egymást részben átfedő, de nem teljesen azonos – jelentés mellett használjuk ugyanazt a nyelvi jelet, a 'megengedés' terminusát. A probléma tisztázásának elvi lehetőségét a logikai hatszög eredményeinek alkalmazása nyújthatja ezen a területen is. A logikai hatszög "felfedezése" után G. Kalinowski vezette be a deontikus hatszög fogalmát. [♦] Az univerzális deontikus kategóriák, a kötelező (obligatory) és a tiltott (forbidden) fölöttes kategóriájaként be kell vezetnünk a preskriptív (prescriptive) fogalmát, ami a deontikus hatszög (U)-sarkába "kerül". A két partikuláris deontikus kategóriára használhatjuk a megengedett (permitted), illetve a mellőzhető (omissible) fogalmakat, és ezek fölöttes fogalmaként az (Y)-sarokba betehetjük az opcionális (optional) kategóriát.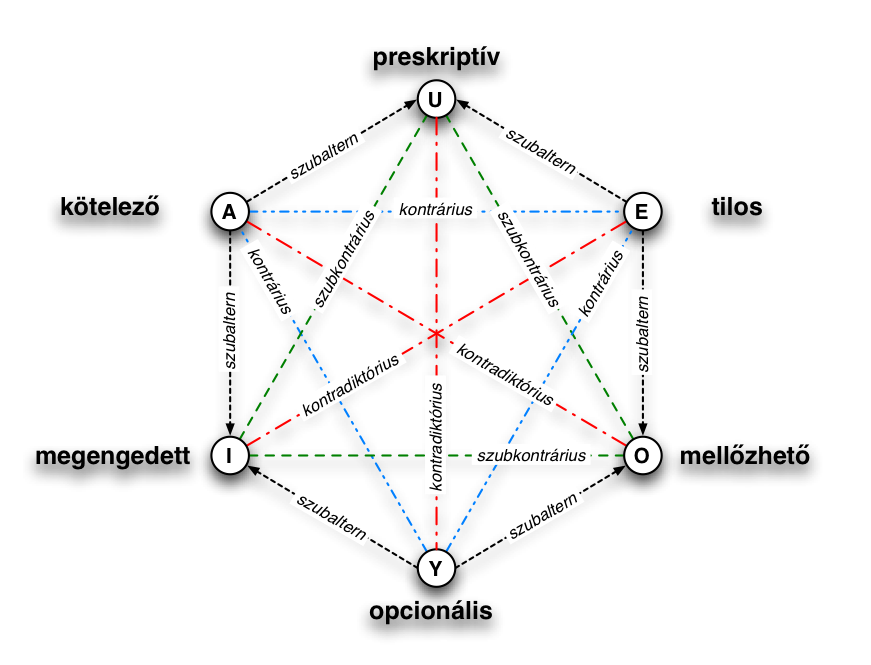
A deontikus logikai hatszög használata ugyanazért kívánatos, mint amiért a logikai hatszöget "szeretjük": egyértelmű kapcsolatok teremthetők így a hatszög kategóriái között (kontradiktórius, kontrárius, szubkontrárius), illetve olyan kategoriális felosztáshoz juthatunk, amelyre már érvényesül a JEPD-elv (ami a logikai négyzet elemeire nem teljesült). Utóbbi szempont (elvárás) nagyon fontos mozzanat. Már Jeremy Bentham is törekedett arra, hogy a JEPD-elvnek megfelelő felosztást használjon a jogi relációk között [LarsL] ezért alkalmazta azt a kategóriahármast (kötelezés, a tiltás és a nem tiltás és nem kötelezés), ami teljesen egybevág a deontikus logikai hatszög kontrárius viszonyban levő fogalmainak csoportjával. Ugyanezt az összefüggést szemléltethetjük a deontikus logikai operátorok egymáshoz való viszonyát bemutató ábrán is:
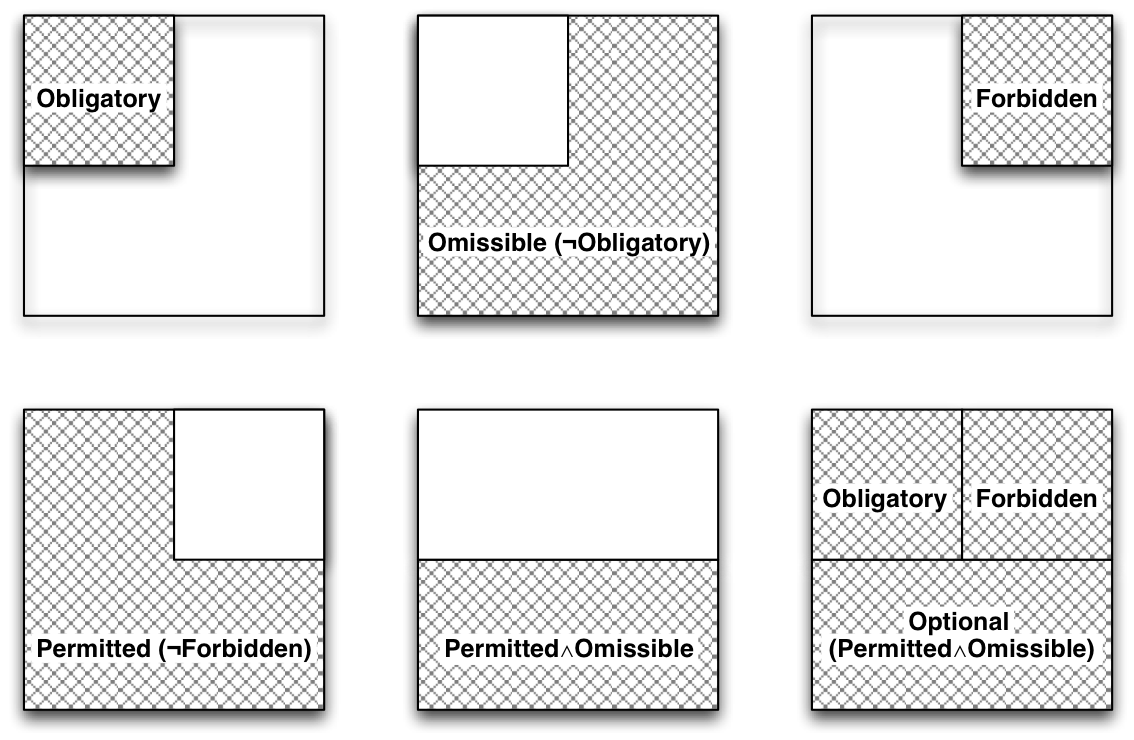
Az ábra szépen mutatja, hogy bár a két univerzális fogalom, a kötelező (obligatory) és a tiltott (forbidden) egymást kizáró kategóriák, a két partikuláris kategória, a megengedett (permitted) és a mellőzhető (omissible) egyszerre vannak átfedésben egymással, illetve valamelyik preskriptív fogalommal. Ezek az átfedések okozzák a deontikus operátorok kezelésének nehézségeit, pongyolaságát. A JPED-elv viszont fennáll a két preskriptív kategória (kötelezés és tiltás), valamint a két partikuláris kategória konjunkciója, tehát az opcionális (optional) kategória között. Természetesen a deontikus logikai hatszög elfogadása, alkalmazása nem ígér csodát. Bevezetése "mindössze" azt az előnyt ígéri, hogy sok esetben azonosítani tudjuk, hogy valamely konkrét nyelvi megnyilatkozáshoz melyik fogalmat (logikai kategóriát) kell hozzárendelnünk. A fejezet első felében bemutatott konkrét mondatainkra visszautalva: az első példa a deontikus logikai hatszög (I)-sarkába, a második az (Y) pontjába, a harmadik pedig az (O) esetbe tartozik.
Sztenderd deontikus logika
A korábban bemutatott modális axiómák közül a (D) deontikus axióma (☜) jelenti a kulcsot a sztenderd deontikus logika (Standard Deontic Logic, SDL) felépítéséhez. A deontikus logikai séma definiálásakor a szükségszerű, illetve a lehetséges ($\Box$, illetve $\Diamond$) modális operátorok helyett ezek deontikus megfelelőit ($\b{O}$, illetve $\b{P}$) használhatjuk. A deontikus operátorok hatókörében levő A szimbólum nem egy cselekvés neve (ahogy azt von Wright még az első modelljében tételezte), hanem egy olyan propozíció jele, amely azt írja le, hogy az adott cselekvést végrehajtották (ezt az értelmezést Prior javasolta először). A deontikus logikai szakirodalomban elterjedt felfogás szerint tehát $\b{O}(A)$ interpretációja: 'kötelező, hogy az a helyzet megvalósuljon, amelyet az A leíró mondattal fejezünk ki' [JrgHa] A továbblépéshez rögzítenünk lell a deontikus logika nyelvét.$\mathscr{L}_{DL}$($\mathscr{L}_{QL}, \b{O})$
| $\mathscr{L}_{QL}$ | propozícionális logika |
| $\b{O}$ | kötelező deontikus logikai operátor |
$\concept{PERMITTED}(A)\equiv \b{P}(A)\defi\lnot \b{O}(\lnot A)$
megengedett (hun) – permitted (eng)
$\concept{FORBIDDEN}(A)\equiv \b{F}(A)\defi \b{O}(\lnot A)$
tiltott (hun) – forbidden (eng)
$\concept{(EXT)}\defi$ Ha $\vdash A\leftrightarrow B$, akkor $\vdash\b{O}(A)\leftrightarrow\b{O}(B)$
extenzionalitás elve (hun) – principle of extensionality (eng)
$\concept{(M)}\defi \b{O}(A \land B) \rightarrow (\b{O}(A) \land \b{O}(B))$
monotonitás elve (hun) – principle of monotony (eng)
$\concept{(C)} \defi (\b{O}(A) \land \b{O}(B)) \to \b{O}(A \land B)$
kumulativitás elve (hun) – principle of cumulativity (eng)
$\concept{(D')} \defi \b{O}(A) \to \b{P}(A)$
deontikus axióma (hun) – deontic axiom (eng)
$\concept{(N)} \defi \b{O}(A \lor \lnot A)$
deontikus szükségességi szabály (hun) – deontic necessitation rule (eng)
Az első két formula azt fejezi ki, hogy megengedett az A cselekvés akkor és csak akkor, ha nem kötelező tartózkodni a végrehajtásától, illetve tiltott az A cselekvés akkor és csak akkor, ha kötelező tartózkodni a végrehajtásától. Az extenzionalitás elve értelmében ha A kötelező ($\b{O}(A))$, akkor minden vele ekvivalens B propozíció is kötelező ($\b{O}(B))$, a monotonitás elve szerint ha A és B együttesen kötelező, akkor egyenként is az, a kumulativitás elve pedig annyit jelent, hogy ha A és B kötelező, akkor ketten együtt is azok (ez a monotonitás elvének megfordított fennállását fejezi ki). A deontikus axióma azt rögzíti, hogy ha az A cselekvés kötelező ($\b{O}(A))$, akkor megengedett is egyben ($\b{P}(A))$, végül a deontikus szükségességi szabály értelmében ha valami tautológia, akkor az kötelező. Hansen megadta azt is, hogyan teremthető kapcsolat von Wright deontikus logikájával. Az (M) és (C) axiómák alapján levezethető von wright-i disztribúció elv, miszerint: $(\b{P}(A) \lor \b{P}(B)) \to \b{P}(A \lor B)$. A (D') séma ekvivalens pedig a von wright-i megengedés elvével (principle of permission), ami így néz ki: $\b{P}(A) \lor \lnot\b{P}(A)$. Mindezek alapján definiálhatunk egy deontikus nyelvet és egy arra épülő deontikus logikai rendszert.A deontikus logika $\mathscr{L}_{DL}$ ábécéje megegyezik a propozícionális logika $\mathscr{L}_{PL}$ nyelvével, amely tartalmazza még az '$\b{O}$' deontikus operátort. Az $\mathscr{L}_{DL}$ nyelvet ugyanúgy definiáljuk, mint a $\mathscr{L}_{PL}$ propozícionális logika nyelvét annyi többletszabály tételezésével, hogy ha $\textit{A}\in\mathscr{L}_{DL}$, akkor $\b{O}(A)\in\mathscr{L}_{DL}$ is igaz. A $\b{P}(A)$ megengedés operátorával rövidíthetjük a $\lnot\b{O}(\lnot A)$, illetve a $\b{F}(A)$ tiltás operátorával $\b{O}(\lnot A)$ kifejezéseket.
deontikus logikai nyelv (hun) – The Language of Deontic Logic (eng)
Az ${SDL}$ az a legkisebb halmaz, amely tartalmazza a $\mathscr{L}_{DL}$ nyelv öszes tautológiapéldányát, az (M), (C), (D') és (N) axiómasémákat, valamint zárt az (Ext) és a modus ponens szabályaira nézve.
szenderd deontikus logikai rendszer (hun) – The System SDL (eng)
Megemlítem, de mivel nem használom a modellépítésben, nem mutatom be azt a továbbfejlesztési irányt, amely a deontikus logikai hatszög további kiterjesztéseként tekinthető: Alessio Moretti, The Geometry of Standard Deontic Logic [Aless]A deontikus logika redukciója az alethikus logikára
Egymástól függetlenül, szinte teljesen egyidőben, lényegét tekintve ugyanazt a redukciós programot fogalmazta meg Stig Kanger [StigK] és Alan Ross Anderson [AlanR] [Ander] [AlanR] [Ander] Anderson H.B. Bohnert 1945-ből származó javaslatát formalizálta, amely szerint a deontikus logikát vissza lehet vezetni az alethikus logikára úgy, hogy a deontikus operátorokat a szankció, szankcionálás fogalmára hivatkozva definiáljuk. Ehhez a normál alethikus logika elméletére (kalkulusára), az alethikus logika szükségszerű, illetve lehetséges ($\Box$, illetve $\Diamond$) operátorára, valamint egy új kategóriára, az előírt cselekvés végre nem hajtásakor kiszabandó S szankció fogalmára van szükség (Anderson olykor szankció-logikaként hivatkozott az új logikára). Az új elemként bevezetett fogalmat később elnevezték prohairetikus konstansnak (prohairetic constant), leginkább azért, mert Kanger is hasonló megfontolásokat követve szintén egy új fogalom felvételét javasolta az alethikus logika sémája mellé, de ő nem a szankciót, hanem a morál által előírt Q cselekvést (pontosabban az azt leíró propozíciót) emelte be a modelljébe. A két javaslat teljesen ekvivalens egymással [JrgHa] mégha a kötelezés deontikus operátorának definíciója el is tér egymástól a két esetben:$\b{O}_Q(A)\equiv\b{O}(A)\equiv\concept{OBLIGATORY}(A)\equiv\b{O}A \defi \Box(Q \rightarrow A)$
kötelező (Kanger értelmezése) (hun) – obligatory interpreted by Kanger (eng)
$\b{O}_S(A)\equiv\b{O}(A)\equiv\concept{OBLIGATORY}(A)\equiv\b{O}A \defi \Box(\lnot A \rightarrow S)$
kötelező (Anderson értelmezése) (hun) – obligatory interpreted by Anderson (eng)
Ezt a redukciót természetesen alá lehet támasztani megfelelő axiómákkal is. A kétféle értelmezéshez egyrészt hozzá lehet rendelni a modális (D) axióma kétféleképpen interpretált formuláját.$\concept{(D}_s\concept{)}\defi \Diamond\lnot\textit{S}$
(D) modális axióma (Anderson értelmezése) (hun) – (D) modal axiom interpreted by Anderson (eng)
$\concept{(D}_q\concept{)}\defi \Diamond\textit{Q}$
(D) modális axióma (Anderson értelmezése) (hun) – (D) modal axiom interpreted by Anderson (eng)
A (D$_q$) formulát tehát értelmezhetjük úgy, miszerint 'lehetséges, hogy Q igaz', míg a (D$_s$) formula interpretációja az lehet, hogy 'lehetséges, hogy S hamis', vagy másként: 'a szankcionálás kontingens, nem szükségszerű'. Ezenfelül mindkét esetben fenntarthatjuk még, hogy a következő tételek teljesülnek.$\concept{(K)} \defi \Box(\textit{A} \to \textit{B}) \to (\Box\textit{A} \to \Box\textit{B})$
(K) modális axióma (hun) – (K) modal axiom (eng)
$\concept{(RN)}\defi \vdash \textit{A} \to\; \vdash \Box\textit{A}$
(RN) modális axióma (hun) – (RN) modal axiom (eng)
A (K) modális logikai séma azt követeli meg, hogy ha egy kondicionális szükségszerű, akkor a szükségszerű előtag materiálisan implikálja a szükségszerű utótagot, míg az (RN) követelmény azt fejezi ki, hogy ha az A a nyelv eleme, akkor a $\Box$A kifejezés is az. Az eddigiek alapján természetesen már definiálhatjuk a deontikus operátorokat is.$\b{O}_S(A)\equiv\b{O}(A)\equiv\concept{OBLIGATORY}(A)\equiv\b{O}A \defi \Box(\lnot A \rightarrow S)$ $\b{P}_S(A)\equiv\b{P}(A)\equiv\concept{PERMITTED}(A)\equiv\b{P}A \defi \lnot\Box\lnot(A \land \lnot S)$ $\b{F}_S(A)\equiv\b{F}(A)\equiv\concept{FORBIDDEN}(A)\equiv\b{F}A \defi \Box\lnot(A \land \lnot S)$ $\b{N}_S(A)\equiv\b{N}(A)\equiv\concept{OMISSIBLE}(A)\equiv \b{N}A \defi \lnot \Box(\lnot A \rightarrow S)$ $\b{D}_S(A)\equiv\b{D}(A)\equiv\concept{PRESCRIPTIVE}(A)\equiv \b{D}A \defi \lnot \Box(\lnot A \rightarrow S)$ $\b{A}_S(A)\equiv\b{A}(A)\equiv\concept{OPTIONAL}(A)\equiv \b{A}A \defi \lnot \Box(\lnot A \rightarrow S)$
Érdemes némi magyarázatot adni arra, miért pont az adott rövidítéseket használták. Nos, az 'optional' az 'Alternative', a 'prescriptive' a 'Dominated', az 'omissible' pedig a 'Non-obligatory' szavak kezdőbetűjére utal. Az andersoni és kangeri megközelítések közti különbséget pedig az fejezi ki, hogy amíg Kanger egy ideális világor feltételezett, addig Anderson egy szubideális világot tett a magyarázatának kiindulópontjába. Bár itt nem jogelmélettel foglalkozunk, mégis érdemes felidézni a híres jogtudós, Hans Kelsen jogfelfogását – egy másik híres jogtudós, H.L.A. Hart interpretálásában:
"A jog az az elsődleges norma, ami szankciót állapít meg. Nincs olyan törvény, ami tiltja az emberölést, csak olyan törvény van, ami arra utasítja a hivatalos személyeket, hogy bizonyos feltételek esetén bizonyos szankciókat alkalmazzanak azokra, akik megölnek valakit." [hart:]
Az idézetből ugyan nem derül ki egyértelműen, de tény, hogy Kelsen a jog fogalmát a szankció fogalmából eredeztette, amit más jogtudósok vitattak ugyan, de ez számunkra itt nem lényeges. Az viszont fontos, hogy pontosan ezt a kelseni megközelítést reprodukálta a logika nyelvén Anderson és Kanger deontikus logikai redukciója. Peng-Hsiang Wang – Kangerék után jó ötven évvel – arra vállalkozott, hogy tisztázza, összeegyeztethető-e Kelsen jogfelfogása és Anderson deontikus logikai elmélete [Peng-] A válasza az lett, hogy igen, de ehhez részlegesen át kell alakítani az andersoni formalizmust az alapján, ahogy von Wright különbséget tesz a kétfajta Ought kategória, a deontikus és technikai kötelezőség között. Nem mutatom be, csak az érdekesség kedvéért említem meg, hogy J.J.C. Meyer az andersoni alapokat integrálta a dinamikus logikával, és így a szokásostól eltérő felépítésű deontikus logikát dolgozott ki [Meyer]Kellellentétes parancs paradoxona
Arthur N. Prior fedezte fel elsőként a materiális implikáció analógiájaként megteremtett deontikus logikai implikációval kapcsolatos paradoxont [A.N.P] Tanulmányában – von Wright pár évvel korábban kidolgozott deontikus rendszerére utalva – Prior először rögzíti azt a nyilvánvaló tényt, hogy egyfelől az implikáció átírható konjunktív alakba, másfelől a kötelezés traszformálható megengedésbe, így az alábbi átalakítások érvényesek.
1)
Kötelező, hogy valaki átmenjen segíteni a szomszédjának.
2)
Kötelező, hogy ha valaki átmegy segíteni, akkor előtte szólnia kell, hogy megy.
3)
Kötelező, hogy ha valaki nem megy segíteni, akkor tilos előtte szólnia, hogy megy.
4)
Valaki nem megy át.
| i) | $\b{O}(A)$ | $\b{O}(A \to B)$ | $\lnot A \to \b{O}(\lnot B)$ | $\lnot A$ |
| ii) | $\b{O}(A)$ | $\b{O}(A \to B)$ | $\b{O}(\lnot A \to \lnot B)$ | $\lnot A$ |
| iii) | $\b{O}(A)$ | $A \to \b{O}(B)$ | $\b{O}(\lnot A \to \lnot B)$ | $\lnot A$ |
| iv) | $\b{O}(A)$ | $A \to \b{O}(B)$ | $\lnot A \to \b{O}(\lnot B)$ | $\lnot A$ |
$\nvdash\lnot A \to \lnot\b{O}A$
(T) axióma kontraponáltja (hun) – contraposition of (T) axiom (eng)
Természetes nyelven ezt úgy fejezhetjük ki, hogy ha nem áll fent egy A propozícióval leírt cselekvés, abból még nem következik az, hogy ne lenne az a cselekvés kötelező. Ez teljesen egybevág azzal a mindennapos tapasztalattal, hogy a normákat nem egyszer megsértik az emberek, de ettől a normák még nem vesztik el az érvényességüket.Diadikus deontika
A kellellentétes vagy általában a feltételes parancsokkal kapcsolatos problémák megoldásának reményében dolgozták ki a diadikus deontikát, vagyis a diadikus deontikus logikát, amit – a monadikus deontikával szemben – képessé tettek arra, hogy a feltételes kötelességet (conditional obligation) kezelni lehessen vele. Von Wright már 1956-ban javasolta, hogy be kellene vezeti a diadikus deontikus operátorokat (dyadic deontic operator), amelyek alkalmazásával kivédhetővé válnak a jelzett gondok [G.H.v] A diadikus formulát a következő alakban javasolta felírni.$\b{O}_d(A/B)\equiv\b{O}(A/B) $
feltételes kötelezettség (hun) – conditional obligation (eng)
A formulát úgy kell értelmezni, hogy az A-val jelölt cselekvés kötelező feltéve, hogy a B feltétel érvényes. A diadikus deontikus logikai operátorok segítségével természetesen ki lehet fejezni a monadikus operátorokat is. Ehhez a feltételként egy tautológiát kell megadnunk, aminek eredményeként az operátorunk feltétel nélkülivé "változik".$\b{O}_m(A)\equiv\b{O}(A)\equiv\b{O}A \defi \b{O}(A/\top)$
feltétel nélküli kötelezettség (hun) – categoric obligation (eng)
ahol $\b{O}_m$ a monadikus operátort, $\top$ a tautológiát jelöli. Von Wright megoldása a jó irányba tett lépésként tekinthető, azonban ő még nem épített fel egy teljes diadikus logikát erre a feltételes formulára. Bengt Hansson volt az, aki egy 1969-es tanulmányában rendszerszerűen dolgozta ki a diadikus deontikus logika (Dyadic Deontic Logic, DDL) teljes struktúráját [Bengt] így őt tekinthetjük a DDL kidolgozójának. Hansson rendszerét pár évvel később axiomatizálta Wolfgang Spohn [Wolfg] és azóta sokan mások is hozzájárultak az új deontika építéséhez [Lenna] A diadikus deontikákra azért van szükség – persze sok minden más mellett –, mert a normák nem mindig vezethetők vissza egyértelműen a jó és a rossz szembeállítására. Le lehet-e lőni a terroristák által eltérített, utasokkal teli repülőgépet, ha tudni lehet, hogy még nagyobb kárt akarnak okozni vele a terroristák? Ezer ilyen kérdést produkál az életünk. A diadikus logika segítségével – mégha a gyakorlati életben megoldani nem is tudjuk az effajta problémákat – legalább elméletileg meg tudjuk ragadni őket úgy, hogy közben mentesülünk a logikai paradoxonoktól. Mint minden más logikában, úgy a deontikus logikán belül is vannak paradoxonok. Ezek jelentős része a klasszikus deontikus logikában bukkant fel, és részben ennek a ténynek köszönhető, hogy az idők során kidolgoztak olyan nem-klasszikus deontikákat, amelyek létrehozásával pont az effajta ellentmondásokat akarták kiküszöbölni. A Jörgensen dilemma abban az értelemben még nem is sorolható a paradoxonok körébe, hogy nem klasszikus logikai paradoxont ír le, hanem azt a kérdést "feszegeti", hogy miként lehet egyáltalán a kijelentések világából átlépni a kellések világába [Jorge] A deontikus logikai paradoxonok közül talán az első lehetett a felfedezőjéről elnevezett Ross paradoxon [AlfRo] A klasszikus példa szerint abból a felszólításból, hogy Küldd el a levelet vagy égesd el!, a klasszikus deontikus logika alapján levezethető az a parancs is, hogy Égesd el a levelet!, ami nyilván ellenkezik az intuíciónkkal. Meglepő paradoxont produkál a szabad választás engedélye (free choice permission) [David] Vegyünk a következő példát. Fred vagy Bill jöhet. Ez az engedély ekvivalens azzal a mondattal, hogy: Fred jöhet, és Bill jöhet. Ez pedig furcsa, mert egy diszjunkcióból konjunkciót kaptunk, amikor az engedélyezés deontikus hatókörét kiterjesztettük a belső diszjunkció tagjaira. Jennings általánosította ezt a problémát úgy, nem csak az engedély hatályába tartozó cselekvésekről lehet szó, de a cselekvőkre vonatkozó diszjunkció is okozhat gondot [R.E.J] Jennings szerint akkor is jelentkezhetnek hasonló problémák, ha elhagyjuk a deontikus logika világát. Bizonyságul erre két példát is bemutatott. Először az összehasonlítások világából hozott egy mondatot: Pierre fontosabb mint William vagy Réné, aminek kiterjesztő átalakítása meghagyja az eredeti mondat jelentését: Pierre fontosabb, mint William, és Pierre fontosabb, mint Réné. Jennings másik példája minden eddiginél egyszerűbb, leírása nem igényel semmi különös logikát, de a probléma ebben az esetben is jelentkezik. Vegyük az alábbi mondatot: Ha Laurie vagy Alison távozik, akkor távozom én is. Ez a mondat ugyanúgy egészíthető ki, mint az eddigiek: a kiegészítés közben a konjunkciót kell használjuk. Az átalakított mondat így néz ki: Az "igazi" deontikus logikai paradoxonok közé tartozik a jó szamaritánus paradoxona (Good Samaritan's Paradox), aminek a lényegét először A.N. Prior írta meg [A.N.P] [Prior] A paradoxon arról szól, hogy ha létezik az a parancs, hogy segítenünk kell a nélkülöző vagy a megtámadott embernek, akkor abból – SDL alapon – levezethető az, hogy léteznie kell nélkülöző és megtámadott embereknek. Igazából Lennart {\AA}qvist cikke tette ismertté a paradoxont [Lenna] és ő volt az is, aki összekötötte a kérdést a kellellentétes parancsok problémájával. A paradoxon feloldható a diadikus denotikus logika (DDL) segítségével: [JrgHa] A szelíd gyilkos paradoxona (gentle murderer' paradox) James William Forrester nevéhez köthető [James] és röviden úgy összegezhető, hogy (i) ha van egy feltételes parancsunk, miszerint "ha gyilkolsz, legalább gyengéden (értsd: minél kisebb fájdalommal) tegyed", illetve tudjuk, hogy egyfelől (ii) valaki gyilkosságot követ el, másfelől (iii) ha valaki gyengéden gyilkolt, akkor gyilkolt is egyben, akkor mindezekből levezethető az, hogy (iv) annak a valakinek gyilkolnia kellett. Ez a paradoxon is feloldható a DDL segítségével [JrgHa] Bemutatás nélkül hivatkozom még az E.J. Lemmon által megfogalmazott Platon dilemmájára (Plato's Dilemma) [E.J.L] az A.N. Priorhoz köthető elköteleződés paradoxonára (paradox of commitment) [A.N.P] valamint a Sven Ove Hansson által explikált tudó (knower) paradoxonára [SvenO] [James] illetve bosszúálló paradoxonára (revenger's paradox) [SvenO] A deontikus logika fejlődéséhez nagyban hozzájárult az a tény, hogy az 1970-es években a téma iránt érdeklődő mérnökökből, filozófusokból, logikusokból kialakult egy szakmai közösség. A közösséget magát, valamint a kétévente megrendezett konferenciáikat szimbolikusan jelző $\Delta$EON kifejezésre utalva $\Delta$-közösségnek nevezem őket. Gondolkozásuk fejlődéséről, az érdeklődési fókusz eltolódásairól, a legfontosabbnak tartott kérdések változásairól, a legfontosabb problémák bemutatásáról több tanulmányt is tudok ajánlani az érdeklődők számára [JrgHa] [Guido] [J.Han] Az egyik cikk szerint az egymást követő évtizedekben az alábbi címszavak álltak a deontikus logikával foglalkozó szakemberek fókuszában.| szakasz | rendszer | fő érdeklődési kör | ||||||||||||
| 50s | monadikus modális logika | $\b{O}$ és $\b{P}$ viszonya | ||||||||||||
| 60s | diadikus modális logika | kapcsolat $\b{O}$ és a tények, normasértések között, szubidealitás és optimalitás, CTD | ||||||||||||
| 70s | temporális deontikus logika | $\b{O}$ és az idő viszonya | ||||||||||||
| 80s | cselekvési deontikus logika | $\b{O}$ és a cselekvés viszonya | ||||||||||||
| 90s | támadható deontikus logika | dilemmák, CTD | ||||||||||||
| 00s | felszólítások, normatív rendszerek | Jörgensen dilemma | ||||||||||||
| modalitás | szankció elvégzésekor | szankció mellőzésekor | ||||||||||||
| megparancsolt | nincs semmi | büntetés | ||||||||||||
| ajánlott | jutalom | nincs büntetés | ||||||||||||
| tiltott | büntetés | nincs semmi | ||||||||||||
| helytelenített | nincs büntetés | jutalom | ||||||||||||
| közömbös | nincs semmi | nincs semmi | ||||||||||||
Társadalmi cselekvés
"Csak egy társadalomtudomány van."
[JackH]
A népi bölcsesség szerint a nevelés során két mondatot ismételgetünk folyamatosan: Kezdd már el! és Hagyd már abba!
"Aki felismeri a tettben a tétlenséget és a tétlenségben a tettet, az olyan ember a bölcs, az olyan az önmagát fegyelmező, bármely tettet végez." (Bhagavad Gítá, IV.18.)
$\mathscr{L}_{JAL}$($\mathscr{L}_{PL}, \mathbb{S}, \mathbb{A}, \Phi, \mathbb{C})$
| $\mathscr{L}_{ML}$ | modális logika |
| $\mathbb{S}$ | világállapotok halmaza |
| $\mathbb{A}$ | ágensek halmaza |
| $\Phi$ | vélemények halmaza |
| $\mathbb{C}$ | választások halmaza |
Cselekvés
A cselekvéselmélet központi kategóriája a társadalmi cselekvés. Ezt a fogalmat Max Weber is a kategóriatana középpontjába helyezte, és Weber meghatározása azóta is igazodási pontot jelent sok társadalomtudós számára. Én is ebből az értelmezésből fogok kiindulni. A weberi cselekvésfogalmat felidézve azonban látni fogjuk, hogy ez a meghatározás nem is olyan egyszerű, és komolyabb explikációs munkát kell belefektetni, hogy pontos definíciót adhassunk. A társadalmi cselekvés fogalmának weberi értelmezését akkor érthetjük meg pontosan, ha követjük azt az logikát, ahogyan Weber összekapcsolja egymással a cselekvéselmélet négy alapfogalmát, a viselkedés, a cselekvés, a társadalmi cselekvés és a társadalmi kapcsolat kategóriáját. A viselkedés fogalmát explicit módon ugyan nem definiálja Weber, de a cselekvés fogalmának meghatározásából kibontható, mit gondol róla. A cselekvés fogalmát Weber az alábbiak szerint határozta meg." … » cselekvésnek« nevezünk minden emberi viselkedést (mindegy, hogy külső vagy belső ténykedésről, valaminek az elmulasztásáról vagy eltűréséről van-e szó), ha és amennyiben a cselekvő, illetve a cselekvők valamilyen szubjektív értelmet kapcsolnak vele össze." [weber]
Kezdjük a definíció egyik könnyebben értelmezhető elemével: a cselekvéshez kellenek cselekvők, cselekvésre képes ágensek. Hogy mit tarthatunk ágensnek, azon belül pedig mit tarthatunk emberi cselekvőnek, azt itt nem tárgyalom. Elegendőnek tartom azt állítani, hogy a cselekvők azok az ágensek, akik képesek cselekvésre, vagyis a cselekvés minőségére vezetem vissza a cselekvő fogalmát. Lépjünk tovább a weberi definíció következő elemére. A definícióban benne van egyfelől a viselkedés fogalmának implicit meghatározása, másfelől a viselkedéshez képest a cselekvés fogalmában benne levő többlet explicit megadása. Viselkedés lehet valamilyen 'ténykedés' (tevés), 'mulasztás' vagy 'tűrés' (tartózkodás), illetve mindezek lehetnek 'belső' vagy 'külső' viselkedések. Viselkedés lehet, ha valaki énekel, eszik, sétál, olvas, becsukja az ajtót, gondolkozik, segít valakin, adót fizet vagy nem fizet adót. A viselkedés (magatartás) a világ lehetséges állapotai között lehetséges transzformációkkal hozható kapcsolatba. Ha az asztalon van egy virsli és én megeszem, akkor a viselkedésem eredményeként a következő világállapotban már nem lesz a virsli az asztalon (a gyomromban lesz). A viselkedésnek ezt az értelmezését persze Weber nem bontja így ki, de megteszik ezt helyette mások. Hogy hogyan, azt kicsit később fogom bemutatni. A viselkedés és a világállapot-transzformációk összekapcsolásával csak annyi a "baj", hogy ezt a meghatározást kiterjeszthetjük minden élőlényre vonatkozóan. Nem véletlen ezért az, hogy Weber még hozzátesz valamit a cselekvés fogalmának definíciójához. Szerinte ugyanis a cselekvésről csak akkor beszélhetünk, ha a "cselekvő szubjektív értelmet kapcsol" a viselkedéséhez. A cselekvés kategóriája ezáltal egyfelől a viselkedés fogalmának generikus alárendeltje lesz, másfelől a "szubjektív értelem" minőségével egy olyan értelmezési réteget hoz be Weber a cselekvéselméletbe, amely segítségével el lehet különíteni az emberi cselekvéseket és állati (olykor emberi) viselkedéseket egymástól. A weberi szubjektívértelem-adás a viselkedéshez kapcsolható intencionalitás fogalmával ragadható meg igazán, aminek jelentését Weber nem adja meg, csak néhány példát mutat be ezzel kapcsolatban. Az intencionalitás kategóriáját, valamint a belőle kibontható további fogalmakat – jelentőségük miatt – külön fejezetben tárgyalom (☜) A cselekvés fogalmához elegendő egyetlen ágens feltételezése. Amennyiben egy cselekvő szubjektív értelmet kapcsol a viselkedéséhez, akkor már cselekvésről beszélhetünk. Ekkor azonban a cselekvésnek még nem tulajdoníthatunk társadalmi minőséget. [♦] A társas, társadalmi jelleg létezéséhez, létrejöttéhez szükség van legalább egy másik ember "jelenlétére". Ezt a mozzanatot Weber – a társadalmi cselekvés meghatározásakor – a következő módon ragadja meg." … » társadalmi« cselekvésnek … az olyan cselekvést nevezzük, amely a cselekvő vagy a cselekvők által szándékolt értelme szerint mások viselkedésére van vonatkoztatva, és menetében is mások viselkedéséhez igazodik." [weber]
Sajnos a társadalmi cselekvés fogalmának weberi definíciójában a 'szándékolt értelem' kifejezés szerepel, ami nem teljesen egyezik meg a cselekvés fogalmában szereplő 'szubjektív értelem' minőséggel. Ez az eltérés kicsit zavaró, mert az előbbi részben mást, részben kevesebbet jelent az utóbbihoz képest. Ez a különbség lényegében megfeleltethető az intencionáltság és az intenció közti fogalmi külnbségnek, amit jobban kibontok az intencionalitásról szóló fejezetben. Ha a jelzett fogalmi pongyolaságtól eltekintünk, akkor a fenti definíció lényegi eleme az, hogy a társadalmi cselekvés fogalmába a "másikhoz való igazodás" minőségével már "belekerül" a társadalmiság mozzanata – még ha gyengébb formában is. Ekkor még mindig elképzelhetünk egyetlen cselekvőt, aki ugyan már társadalmi kötöttségben cselekszik, ha cselekvését valamilyen módon egy másik emberhez igazítja, de ezt még megteheti úgy is, hogy ez az igazodás csak fejben történik meg, valós kapcsolat nem jön létre a cselekvők között. A társadalmiságot igazán jól a társadalmi kapcsolat fogalmával tudja Weber megragadni, amikor már arról van szó, hogy a társadalmi cselekvők kölcsönösen egymáshoz igazodnak a cselekvéseik során, ezt a fogalmat azonban csak később tárgyalom (☜) Ahhoz, hogy jobban megértsük, mi és miért kell társadalmi cselekvésnek tartanunk, jobban ki kell bontanunk az eddig jelzett fogalmi összetevők jelentését. Mielőtt ebbe belevágnék, érdemesnek tartok bemutatni pár példamondatot a cselekvésre, viselkedésre vonatkozóan, hogy a jelenség mélyén rejlő kérdéseket és problémákat jobban érzékelhessük. Nézzük meg tehát, miről is szólnak a következő mondatok.| i.) | Kiszáradt a fű, az eső elmosta a nyomokat. | |||||||||||||
| ii.) | Kati elpirult, amikor Laci ránézett. | |||||||||||||
| iii.) | Nagyot nőtt ez a Peti gyerek. | |||||||||||||
| iv.) | A betörő ott hagyta az ujjlenyomatát az ajtókilincsen. | |||||||||||||
| v.) | Profi volt az elkövető, nem hagyott nyomokat. | |||||||||||||
| vi.) | A sofőr látta a balesetet, de nem állt meg segíteni. | |||||||||||||
| vii.) | Dávid beteg volt, egész nap köhögött. | |||||||||||||
| viii.) | Rita köhögött egyet, ezzel jelezte, hogy ő is ott van a szobában. | |||||||||||||
| ix.) | Jani az izmait megfeszítve pózolt a tükör előtt, amikor görcsbe állt a vádlija. | |||||||||||||
| x.) | Feri egész nap a kertben ásott. | |||||||||||||
| xi.) | Pali bácsi megöregedett. | |||||||||||||
| facere esse | to bring it about | előidézni valamit | ||||||||||||
| non facere esse | to abstain from bringing it about | tartózkodni valaminek az előidézésétől | ||||||||||||
| facere non esse | to prevent from having it come about | megakadályozni valami megtörténtét | ||||||||||||
| non facere non esse | to abstain from preventing from having it come about | tartózkodni valami megtörténésének megakadályozásától | ||||||||||||
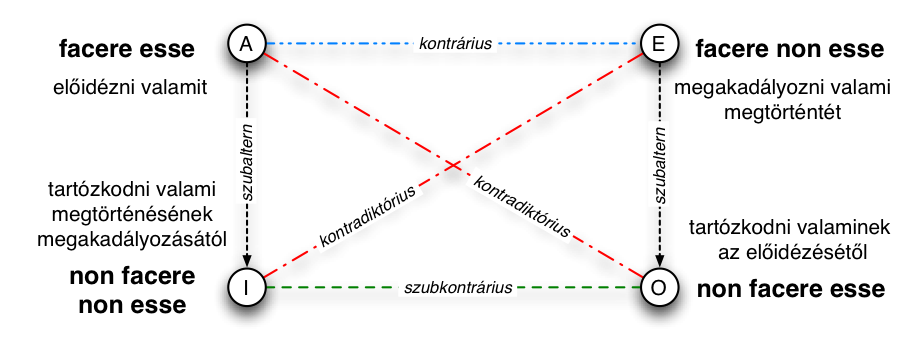
Bár Szent Anzelm pontos és használható tipológiát állított fel, típustana gyakorlatilag feledésbe merült, vagy legalábbis a cselekvéselméleti diskurzus főáramába nem került be. Az anzelmi cselekvéstípusok azonban – persze más terminusokkal megjelölve – felbukkantak a későbbi elméletekben. A cselekvés fogalmának meghatározását keresve sokféle szempont szerint közelítettek a vizsgált jelenséghez. Egyes elméletek azt keresték, hogy lehet detektálni a cselekvéseinkben (vagy az azokat leíró mondatainkban) rejlő intencionáltságot, mások a cselekvés fogalmának logikai összetevőkre bontását végezték el, megint mások a tartózkodás fogalmának megragadására törekedtek. Donald Davidson a cselekvést leíró mondatok specialitását keresve sokféle értelemben (irányban) hasznosítható javaslatot fogalmazott meg, de azzal nem igazán foglalkozott, mit is jelent igazából a cselekvés fogalma [Donal] Tanulmánya végén annyit azért kimondott, hogy a cselekvésről akkor beszélhetünk, ha a viselkedésben intencionalitás van.
" … csak akkor beszélhetünk ágenciáról, ha értelmes az a kérdésfeltevés, vajon az ágens intencionálisan cselekedett-e. Bár, úgy tűnik számomra, vannak olyan esetek is, amikor csak akkor tulajdonítunk ágenciát, ha a kérdésre, vajon az ágens intencionálisa cselekedett-e, a válasz 'igen'. Ha egy ember elesik véletlenül vagy azért, mert egy teherautó elsodorta őt, nem beszélünk ágenciáról; de akkor igen, ha szándékosan esett el." \cite[94]{DonaldDavidson:1966}
Egy másik tanulmányában ezt definíciószerűen ki is mondta, amikor azt állította, hogy " … egy esemény akkor cselekvés, ha intencionálisként írható le." [Donal] Azt azonban nem tisztázta Davidson, mit jelent az intencionalitás, csak a nyelvi intuíciónkra bízta annak eldöntését, mikor és miért érezzük azt, hogy egy mondattal intencionalitást írunk le. Erre a kérdésre az ún. stit-elmélet sem ad(ott) választ, ennek ellenére az elméletet által javasolt tesztet nagyon széles körben elfogadták, elfogadják annak eldöntésére, hogy milyen mondatokra mondhatjuk azt, hogy azok ágentívek, vagyis valamilyen cselekvést írunk le velük. A stit-elméletet Nuel Belnap és Michael Perloff alapozta meg (az első cikkük 1988-ban jelent meg [NuelB] amit két évvel később követett egy javított változat [NuelB] Ming Xu volt az, aki axiomatizálta Belnapék elméletét, így hárman jelentettek meg egy közös könyvet [NuelB] Belnapék több lehetőséget is felsorolnak arra, hogy milyen teszt segítségével lehetne eldönteni a mondatok ágentivitását.| i.) | brings it about that | vi.) | allows it to be the case that | |||||||||||
| ii.) | makes it the case that | vii.) | takes steps in order that | |||||||||||
| iii.) | causes it to be the case that | viii.) | behaves so that in consequence | |||||||||||
| iv.) | is responsible for the fact that | ix.) | sees to it that | |||||||||||
| v.) | lets it be the case that | |||||||||||||
$Q \leftrightarrow [\alpha \;\concept{STIT:} \; Q]$
Belnap-Perloff ágentivitás tézise (hun) – Belnap-Perloff's agentivity theorem (eng)
Mielőtt példát mutatnék a stit-operátoros teszt alkalmazására, meg kell még mutatnom azt is, hogy milyen magyar fordítást használhatnánk a stit-operátorban levő 'sees to it that' angol kifejezés helyett. Nem könnyű feladat a fordítás itt. A legtöbbször alkalmazható megoldás a 'gondoskodik róla, hogy' fordulat lehetne, de bizonyos kontextusokban használható lenne a 'törekszik arra, hogy', 'tesz róla, hogy', a 'gondja van rá, hogy' vagy az 'ügyel arra, hogy' kifejezés is. Amennyiben nem okoz zavart, az egyszerűség kedvéért elhagyhatjuk az ágensre utaló paramétert a formulából, és csak a cselekvés tartalmát jelző paramétert hagyhatjuk meg benne. Ilyen esetben a Q paramétert tehetjük zárójelek közé: $stit:(Q)$. A stit-operátort tehát úgy használhatjuk ágencia-tesztelésre, hogy vesszük az eldöntendő mondatot, azt belehelyezzük a stit-kifejezésbe, majd megvizsgáljuk, hogy fennáll-e az ekvivalencia a két propozíció között. Nézzünk meg egy példát! Ha a korábbi listánkból vesszük a Nagyot nőtt ez a Peti gyerek állítást, és erre alkalmazzuk a stit-tesztet, akkor kiderül, hogy ebben az esetben az negatív eredményt ad, hiszen a 'Péter stit (= gondoskodott róla, hogy) Nagyot nőtt ez a Peti gyerek' szemantikailag nem értelmes mondat. Péter növését nem értelmezhetjük saját cselekvéseként. Ezzel szemben a 'Feri stit (= gondoskodott róla, hogy) Feri egész nap a kertben ásott' mondat értelmes a teszt szerint is, és mi is tudjuk, hogy ez a mondat valóban Feri cselekvését írja le. A stit-operátort megbízható tesztként használhatjuk az ágentivitás detektálására, de arra nem alkalmas, hogy fogalmilag pontosan leírhassuk vele az intencionalitás jelenségét. Nem segít sem abban, hogy tipizáljuk, sem abban, hogy logikai összetevőkre bontsuk vele az intencionalitás fogalmát. Ez a "hiány" természetesen nem változtat a stit-operátor hasznosságán a tesztelések során, de azt jelzi, hogy szükséges lesz mondani valamit az intencionalitás fogalmáról – nyilván más eszközökre támaszkodva. Ezt később, egy önálló fejezetben fogom megtenni (☜) Itt most a stit-operátor egy további hasznos vonását mutatom meg. Az operátor segítségével ugyanis könnyen és szemléletes módon kifejezhetjük a tartózkodást megvalósító cselekvéseinket. Mielőtt bemutatnám, hogyan, szükségesnek tartok egy rövidebb kitérőt tenni a tartózkodás fogalmával kapcsolatban.A tartózkodás mint tétlen tett
Utaltam már rá, hogy a hétköznapi, reflektálatlan gondolkodás könnyen egybemossa, azonosítja a cselekvés és a tevékenység, tevés kategóriáit, holott nyilvánvaló, hogy a cselekvés általános fogalma alá két másik alárendelt fogalmat kell besorolnunk: a tevés, megcsinálás, illetve a tartózkodás, tétlenség kategóriáját. Szokás ezeket pozitív cselekvésnek, illetve negatív cselekvésnek is nevezni. Ha valaki jelentéktelen, érdektelen kérdésnek tartaná a tartózkodás jelenségét, akkor annak érdemes belegondolni abba, hogy a sztrájk jelensége a nem-dolgozást (tehát a dolgozástól való tudatos tartózkodást) jelenti, amely igen sok, igen mély konfliktus forrása volt eddig a történelemben. Egy – Csuang-ce, taoista gondolkodótól származó – gyönyörű mondás szerint:" … az ember nem képes a sáros, zavaros vizet megtisztítani, de ha békén hagyja, az magától letisztul." [Hejja]
A taoizmus fontosnak tartja, hogy az emberi viselkedés a Wu-Wei elvhez igazodjon, aminek jelentése: cselekvés nem-cselekvés által. Ezzel voltaképp a tartózkodást írják le. De a történelemben sok helyen felbukkanó passzív ellenállás (Gandhi szatjágraha mozgalma, a erőszakmentes polgári engedetlenség) jelensége is azt példázza, hogy a tartózkodás értelmes, jelentéssel bíró fogalom lehet. A tartózkodást természetes nyelvi kontextusban sokféle alakban kifejezhetjük. Először is bármikor használhatjuk a tevőleges igék tagadó formáját: 'nem csinál meg valamit', 'nem segített neki'. De a negatív cselekvést kifejezhetjük "önálló" módon is. Mondhatjuk, hogy 'tétlenül szemlél', 'tétlenkedik', 'elmulaszt', 'mellőz', 'hagy valamit megtörténni', 'visszafogja magát'. Ha valaki 'enged másnak valamit megcsinálni' vagy 'tűri, hogy más megcsináljon valamit', akkor is tartózkodásról beszélhetünk, bár ekkor már másodrendű cselekvésről van szó. Olykor a 'kiváltság', a 'privilégium', a 'mentesség', az 'immunitás' is jelenthet valamilyen kötelezettség alóli mentességet, ami ebben az értelemben a tartózkodáshoz is kapcsolható. [♦] Viszont ha valaki valamit elfelejt, és ezért nem csinálja meg, akkor azt nem sorolhatjuk a tartózkodás kategóriája alá, mert ebből hiányzik az intencionáltság. A negatív cselekvés vagy a tartózkodás mint "nem-cselekvés" az intenció fogalmával határozható meg a "nem cselekvéshez" vagyis a cselekvés tagadásához képest. A tartózkodás jelenségét azért nehéz megragadni, mert egyszerre tartjuk cselekvésnek, illetve nem-cselekvésnek. Cselekvésként kezeljük, amikor a cselekvés egyik altípusaként értelmezzük, miközben a tartózkodás – egy másik értelemben – nem-cselekvést jelent. Utóbbi fogalom azonban sok mindent jelenthet, és el kell tudnunk választani egymástól a nem-cselekvés kétféle értelmezését. Amikor állok egy ajtó előtt és nem lépek ki rajta, mert nem akarom ezt valamiért, akkor ez az "nem-kilépés" nem-cselekvésnek és tartózkodásnak számít. De ugyanebben a pillanatban még milliónyi más dolgot nem csinálok: nem énekelek, nem beszélek, nem írok könyvet, nem eszem stb. Ezekre a nem-cselekvésekre nem mondhatjuk, hogy tartózkodom ezek végrehajtásától, mert ha így tennénk, akkor végtelen számú cselekvést lehetne (kéne) még felsorolnunk. Amikor tatózkodunk egy cselekvés végrehajtásától, akkor abban van valami többlet az "egyszerű" nem-cselekvéshez képest. Valahogy meg kell különböztetnünk a tartózkodást az ilyen "nem-cselekvésektől". Ezt a többletet úgy foghatjuk meg, hogy azt mondjuk, a tartózkodás intencionális, szándékolt nem cselekvés. Ezt a stit-elmélet segítségével könnyedén kifejezhetjük. Nem kell mást tennünk, mint hogy az intencionális cselekvés tagadását is intencionálisnak kell minősítenünk, vagyis kétszer kell a stit-operátort alkalmaznunk (az egyszerűség kedvéért most elhagyjuk az ágensre utaló paramétert).$\concept{REFRAIN}(Q) \defi \concept{STIT}(\neg \concept{STIT}(Q))$
tartózkodás (hun) – refrain (eng) – forbearance (eng)
A képlet valamely cselekvés elvégzésére irányuló törekvés hiányára való törekvést vagyis a cselekvés nem elvégzésére való törekvést fejezi ki, de egyben mutatja azt is, hogy a tartózkodás – szemben a tevés kategóriájával – másodrendű fogalom. A tartózkodás fogalma arra is alkalmas, hogy segítségével könnyebben el tudjuk különíteni egymástól az intencionalitás cselekvéseket és a nem intencionális viselkedéseket, történéseket. Ha valamilyen viselkedés intencionális, akkor az attól való tartózkodás is az kell legyen. Ha tehát valamely viselkedéstől tartózkodni tudok, akkor az jele az intencionalitásnak, illetve fordítva: ha valamilyen viselkedéstől nem tudok tartózkodni, akkor az nem mondható intencionálisnak. Ha csuklom, ha görcsölök, ha pislogok, ha pirulok, akkor ezeket nem tudom saját akaratomra abbahagyni, tehát nem tudok tartózkodni tőlük. Ha viszont ások a kertben, iszom egy korsó sört, olvasok egy könyvet, akkor ezeket a cselekvéseket meg tudom szakítani, vagyis ilyen esetekben képes vagyok a tartózkodásra.A cselekvés fogalmi összetevői
Mind a tevőleges cselekvés, mind a tétlen cselekvés (tartózkodás) jellemzése során használtam a viselkedés fogalmát, de még nem bontottam ki, mit is kell érteni alatta. A következőkben Georg Henrik von Wrightet követve azt mutatom be, hogy miként lehet a cselekvés fogalmát logikai összetevőkre bontva pontosabban leírni. Mielőtt a fogalmi összetevők kibontásába kezdenék, szükségesnek tartok néhány jelölést bevezetni. Egy formális cselekvéselméleti modellben nyilvánvalóan kulcsszerepe van a cselekvés fogalmának. Az alapkategóriák jelölésére többféle konvenció is létezik, ezek közül nekem is választanom kell, melyiket akarom használni. A választásom von Wright terminológiájára esett, amit a 'Norm and action' című könyvében fejtett ki először [vonwr] Az eddigiekből kiderült, hogy a cselekvés lehet tevés, illetve tartózkodás. Mivel ezeket a későbbiekben gyakran kell majd meghivatkozni, és konzekvens terminológia használatára van szükség, ezért a cselekvés általános fogalmát mostantól kezdve a $\pm$do operátorral jelölöm. Megengedhetőnek tartom, hogy olykor – von Wright megoldását követve – az általában vett cselekvésre az act terminussal hivatkozzak. Amennyiben nem zavaró, vagyis nem okoz többértelműséget, akkor az egyszerűbb do terminust is használhatónak gondolom. Ha a kontextus megkívánja, akkor a do (esetleg a +do) kifejezés a pozitív cselekvést vagyis a tevést, míg a -do terminus a negatív cselekvést vagyis a tartózkodást jelöli. A von wrigth-i do pozitív cselekvésoperátor tartalmilag ugyanazt jelenti és ugyanazt a célt is szolgálja, mint a a Belnapék álta bevezetett stit-operátor. A tartózkodás jelenségére ajánlott stit-megoldás ismeretében viszont arra nagyon vigyázni kell, hogy a negatív cselekvésre vonatkozó $-do$ operátort nehogy úgy értelmezzük, mintha az csupán a pozitív cselekvésoperátor tagadása lenne. Láttuk, hogy a stit-elmélet szerint a tartózkodás másodrendű intencionalitást jelent, ami szintaktikailag azt jelenti, hogy egymásba ágyazott cselekvésoperátorokkal lehet csak pontosan megragadni. A tartózkodást az új terminológia alapján az alábbi módon fejezhetjük ki.$\concept{REFRAIN}\equiv-\concept{DO}\defi \concept{DO}(\neg \concept{DO})\equiv \concept{DO}\neg \concept{DO}$
tartózkodás (hun) – refrain (eng) – forbearance (eng)
Az egyszerűség kedvéért a fenti formulából elhagytuk a cselekvés tartalmára utaló paramétert, de természetesen a cselekvések leírásakor ezt mindig meg kell adni. Von Wright sem gondolja ezt másként, így a következő feladat megnézni, hogy von Wright milyen fogalmi összetevőkre támaszkodva véli felépíthetőnek a cselekvés fogalmát. Az már kiderült, hogy a cselekvés fogalma alatt von Wright is valamilyen ágens által végzett intencionális tevést vagy tartózkodást ért. A kérdés, hogy mire vonatkozik ez a kétféle cselekvési lehetőség. Von Wright válasza erre az, hogy vannak a világállapotok, a világállapotok között átmenetet, változások (transition) valósul(hat)nak meg, és a cselekvéseinket úgy jellemezhetjük, hogy ezek eredményeként a világállapotok közti átmenet(ek) vagy megvalósul(nak) vagy elmarad(nak). A "folyamat" tehát így néz ki.| (i) | $\pm$ do$(T(\pm p,\pm p)) \leftrightarrow$ +do$(T(\pm p,\pm p))\mid$ -do$(T(\pm p,\pm p))$ |
| (ii) | $\pm$ do$(T(\pm p,\pm p)) \leftrightarrow$ do$(T(\pm p,\pm p)) \mid$ -do$(T(\pm p,\pm p))$ |
| (iii) | $\pm$ act$(T(\pm p,\pm p)) \leftrightarrow do(T(\pm p,\pm p)) \mid forbear(T(\pm p,\pm p))$ |
| (iv) | $\pm$ act$(T(\pm p,\pm p)) \leftrightarrow d(T(\pm p,\pm p)) \mid f(T(\pm p,\pm p))$ |
| cselevés feltétele | cselekvés | cselekvés eredménye | ||||||||||||
| $T(p,\neg p)$ | do$(Ego,T(p,p))$ | $T(p,p)$ | ||||||||||||
| p állapot fennáll, de megszűnik, hacsak nem tartják fent | Ego a p állapotot megőrzi | p megmarad | ||||||||||||
| $T(p, \neg p)$ | -do$(Ego,T(p,p))$ | $T(p, \neg p)$ | ||||||||||||
| p állapot fennáll, de megszűnik, hacsak nem tartják fent | Ego hagyja, hogy a p állapot megszűnjön | p megszűnik | ||||||||||||
| $T(p,p)$ | do$(Ego,T(p, \neg p)$ | $T(p, \neg p)$ | ||||||||||||
| p állapot fennáll, és meg is marad, hacsak nem változtatják meg | Ego a p állapotot megváltoztatja | p megszűnik | ||||||||||||
| $T(p,p)$ | -do$(Ego,T(p,\neg p))$ | $T(p,p)$ | ||||||||||||
| p állapot fennáll, és meg is marad, hacsak nem változtatják meg | Ego hagyja, hogy a p állapot megmaradjon | p megmarad | ||||||||||||
| $T(\neg p, \neg p)$ | do$(Ego,T(\neg p,p))$ | $T(\neg p,p)$ | ||||||||||||
| p állapot nem áll fenn, és nem is következik be, hacsak nem állítják elő | Ego a p-t állapotot előállítja | p megtörténik | ||||||||||||
| $T(\neg p,\neg p)$ | do$(Ego,T(\neg p,p))$ | $T(\neg p,\neg p)$ | ||||||||||||
| p állapot nem áll fenn, és nem is következik be, hacsak nem állítják elő | Ego hagyja, hogy a p állapot hiánya megmaradjon | p hiánya megmarad | ||||||||||||
| $T(\neg p,p)$ | do$(Ego,T(\neg p,\neg p))$ | $T(\neg p,\neg p)$ | ||||||||||||
| p állapot nem áll fenn, de bekövetkezik, hacsak nem akadályozzák meg | Ego megakadályozza, hogy a p állapot bekövetkezzen | p hiánya megmarad | ||||||||||||
| $T(\neg p,p)$ | -do$(Ego,T(\neg p,\neg p))$ | $T(\neg p,p)$ | ||||||||||||
| p állapot nem áll fenn, de bekövetkezik, hacsak nem akadályozzák meg | Ego hagyja, hogy a p állapot bekövetkezzen | p megtörténik | ||||||||||||
Cselekvő ágens, Ego és Alter
A társadalmi cselekvés elemzése során ágensekről beszéltem, de eddig nem volt fontos sem az, hogy több cselekvőről beszéljünk, sem az, hogy megkülönböztessük őket egymástól. A társadalmi cselekvések során – akaratlanul is – modellezzük magát a társadalmat is. A társadalom minimális modelljéhez két szereplőre, két ágensre van szükség. Sokáig elég ennyit feltételeznünk, hogy a társadalmi kapcsolatok legelemibb vonásait értelmezhessük. Ehhez viszont meg kell különböztetnünk két szereplőt egymástól, leginkább azért, mert a társadalmi cselekvések megértését vagyis a cselekvéshez kapcsolt szubjektív értelem felderítését úgy remélhetük, ha valamelyik cselekvő szempontrendszerét, optikáját magunkévá tesszük. Ezt a szereplőt Egonak fogom nevezni, és amíg csak lehet, kitartok e név mellett. Ego a cselekvéselméleti modell fokális ágense. A társadalmi kapcsolatot vagy rövidebben a társadalmiságot "reprezentáló" másik szereplő neve Alter lesz. [♦] Mindig Ego cselekvését akarjuk megmagyarázni, tehát az ő személyére fókuszálunk, de a társadalmi cselekvéshez szükséges másik szereplőt, Altert sem hagyhatjuk ki a modellből – mégha tudjuk is, hogy ezzel a névvel a legtöbb esetben csak egy passzív szerepet/szereplőt jelölünk. Amikor a későbbiekben játékelméleti apparátust fogok alkalmazni a társadalmi kapcsolatok modellezésére, akkor látható lesz, hogy a játékelmélet különböző ágaiban a cselekvőkre olykor más neveket aggatnak (Donor, Recipiens, Actor stb.). Ilyen esetekben igazodni fogok az éppen bemutatott elméletek névhasználati konvencióihoz, de minden esetben jelzem majd, hogy az újonnan bevezetett szerepnevek melyik "főszerepnek" felelnek meg (Egonak vagy Alternek). Bármennyire is lényeges kérdés, hogy mit tartunk ágensnek, pontosabban – mivel cselekvéselméleti modellről van szó – mit tartunk emberi ágensnek, és ehhez kapsolódóan mit értünk a tudat fogalmán, e kérdésekre nem próbálok meg választ adni. Sok más diszciplina illetékesebb a válaszok keresésében, az érdeklődők a kognitív tudomány, az elmefilozófia, az intencionalitás filozófiája és még több más diszciplina képviselőitől remélhetnek adekvát magyarázatokat erre.Intencionalitás
A cselekvést a benne rejlő intencionalitás többletével különböztethetjük meg az egyszerű viselkedéstől. Az intencionalitás vizsgálatához a szociológia mellett sok más tudományterület tudására is szükség van, vagyis nem mondhatjuk azt, hogy a szociológia egyedül lenne illetékes e kérdés vizsgálatára, de ezen a ponton azt nem tehetem meg, hogy nem foglalkozom ezzel a problémával. A tudat és az ágencia fogalmának elemzését még átutalhattam más diszciplinák illetékességi körébe, az intencionalitásról mondanom kell valamit. Az intencionalitás mibenlétével kapcsolatban csak rövidebben fejtem ki, amit fontosnak tartok, és ennek során kicsit át kell merészkednem a filozófia területére is, ahol természetesen nagyon félszegen merek csak mozogni, de ezt nem nagyon lehet megúszni. Az intencionalitás fogalmát sokak szerint Franz Brentano emelte be elsőként a tudományos diskurzusba, amikor a pszichikai és fizikai jelenségek közti különbséget keresve az intencionalitást jelölte meg a jelenségeket egymástól elválasztó minőségként. Ha Brentano felfogása a kályha, ahonnan érdemes elindulnuk, akkor nézzük meg először azt, hogy mit is mondott az intencionalitás fogalmáról."Minden pszichikai közös jellemvonása abban található, amit sajnálatos módon gyakran oly félreérthető kifejezéssel tudatnak neveznek, vagyis egyfajta szubjektív magatartásban, egyfajta, mint mondják, intencionális viszonyban, amely valamire irányul, ami talán valójában nem létezik, ám belsőleg tárgyként adott. Nincs hallás valami meghallott, hívés valami elhitt, remény valami reménylett nélkül, nincs törekvés a törekvés célja nélkül, és nincs öröm anélkül, hogy valaminek ne örülnénk, s még sorolhatnánk." [Franz]
Bár ebben az idézetben még nincs egyértelmű fókusz rajta, de azért már szerepel az a gondolat, hogy az intencionalitás egyfajta szubjektív valamire irányulás. Hogy ezt hogy kell értelmezni, később bővebben kifejtem Husserl intencionalitásértelmezése kapcsán. Előtte azonban érdemes felidézni azt, hogy Brentano milyen altípusokat rendelt az intencionalitás fogalma alá.
"Az első alaposztály a legtágabb értelemben vett képzeteké …
A második alaposztály az ítéleteké …
az ítélet alapja, miként a vágyakozásé is, mindig valamilyen képzet; …
Mi tehát a megkülönböztető jegye annak, amikor nem egyszerűen képzetet alkotok, hanem ítélek is? – Ebben az esetben a képzetalkotáshoz egy második, a képzet tárgyára irányuló intencionális viszony is kapcsolódik, a képzet tárgyának elismerése vagy elvetése. Aki Istent említi, Isten képzetét fejezi ki, aki pedig azt mondja: van Isten, arról beszél, hogy hisz benne.
A harmadik alaposztály a kifejezés legszélesebb értelmében vett érzelmi mozgásoké, kezdve attól, hogy valamely gondolat egyszerűen kellemesen vagy kellemetlenül hat rám, egészen a meggyőződésen alapuló örömig vagy szomorúságig, illetve a cél- és eszközválasztás legbonyolultabb jelenségéig. Arisztotelész mindezt az órexisz fogalmában foglalta össze."
[Franz]
"Minden pszichikai jelenség azáltal jellemzett, amit a középkor skolasztikusai intencionális (nyilvánvalóan mentális is) inegzisztenciának (valamire irányuló belső létezésnek) neveztek, s amit mi, habár nem is egészen kétértelműség nélküli kifejezéssel, egy tartalomra való vonatkozásnak, egy tárgyra való irányulásnak (ami alatt itt nem realitást kell érteni) vagy pedig az immanens tárgyiasultságnak nevezhetnénk. Mindegyik magába foglal valamit a tárgyakból, habár nem mindegyik egyenlő módon. A képzetben valamit megjelenítünk, az ítéletben valamit elismerünk vagy elvetünk, a szeretetben valamit szeretünk, a gyűlöletben valamit gyűlölünk, a vágyakozásban valamit kívánunk stb." [Brent]
Ez az idézet is megerősíthet minket abban, hogy az első két irányultságtípusként a képzeteket (vagy fogalmakat), illetve az ítéleteket (vagy propozíciókat) különíthetjük el Brentano nyomán, amelyekhez ráadásul a modern logika eszköztárának igen nagy részét hozzárendelhetjük. Továbbra sem világos azonban az, hogy mit értsünk a harmadik kategória alatt. Brentano ide sorolja mindazt, amire a szeretetünk, gyűlöletünk, vágyakozásunk, bármely érzelmünk, örömünk, bánatunk irányul, de idetartozónak véli a cél- és eszközválasztás bonyolultabb jelenségeit is. Utóbbi mozzanat zavarbaejtő, mert a (cél- és eszköz)választás már a mérlegelés területéhez tartozik, amit viszont nem szoktunk az érzelmi mozgások fogalma alá sorolni, sőt, ezeket sokkal inkább ellentétes lényegű jelenségeknek tartjuk. Mi lehet a megoldás? Brentanonak szerintem igaza van abban, hogy a felsorolt példák mind a harmadik kategória alá tartoznak, de nincs igaza akkor, amikor ezt érzelmi mozgásoknak nevezi. A racionális, mérlegelésen alapuló beállítódásokat valóban élesen szembe kell majd állítanunk az érzelmi cselekvésekkel, de ez nem jelenti azt is egyben, hogy ne lehetne mindezekben valami közös. Ez pedig nem más, mint az arisztotelészi órexisz kategóriája (amit Brentano egyébként áttételesen meg is nevez). Mivel ezt a régi terminust nem akarom továbbvinni, így helyette a továbbiakban a törekvés, késztetés terminusát fogom használni, ami alatt a – képzeteinkre és ítéleteinkre vonatkozó – irányultságaink poláris minőséggel (vonzással vagy taszítással) és motivációs intenzitással ellátott (érték)viszonyulást érthetünk. A késztetéseink azért nagyon fontosak az életünkben, mert ezek aktuális vágyakat és averziókat képesek ébreszteni bennünk, amelyek közül aztán vágyaink egy része a hiteinkkel kombinálódva aktuális szándékokat alakít ki, és ezek végül cselekvésekre sarkallnak minket. A késztetéseink irányultsága azonban egy fontos szempontból eltér az ítéleteink irányultságától. Searle munkássága nyomán vált széles körben ismertté és elfogadottá az a nézet, miszerint az intencionalitás leírásakor annak megfelelési irányát is ki kell fejeznünk [searl] [♦] Ez az irány alapvetően kétféle lehet, világ-szó vagy szó-világ irányú, de Searle szerint elképzelhető olyan helyzet, amikor nincs az intencionálisnak nincs ilyen irányultsága, illetve lehetséges az is, amikor mindkét irány tételeznünk kell. De mit is ért megfelelési irányon Searle? A szó-világ megfelelés azt jelenti, hogy a kimondott, elgondolt ítéleteink tartalmilag a világra irányulnak. Amikor kijelentjük, hogy 'esik az eső', akkor a világ állapota felől érthetjük meg a kimondott mondatunkat. A világ itt adottnak tekinthető, és az intencionalitás funkciója itt a világ leírása. A világ-szó megfelelési irány esetében az intencionalitás funkciója más. Ekkor ugyanis az ágens szeretné valamilyen értelemben megváltoztatni a világot, és ezért a beszédaktusban megnyilvánuló cselekvése a szótól a világ felé irányul. Amikor ígéretet teszünk vagy utasítást adunk valaki másnak, akkor a megnyilatkozásunk arra irányul, hogy a világ valamilyen értelemben megváltozzék. A kétféle megfelelési irány segítségével tehát négyféle esetet képzelhetünk el. Amikor azonban Searle típuskra bontja a beszédaktus fogalmát, akkor ő öt altípust különít el.| beszédaktust | megfeleltetési irány | példák | ||||||||||||
| asszertívum | szó-világ | kijelentés, leírás, osztályozás, magyarázat | ||||||||||||
| direktívum | világ-szó | utasítás, parancs, kérés | ||||||||||||
| komisszívum | világ-szó | ígéret, fogadalom, felajánlás, megállapodás, jótállás, fenyegetés | ||||||||||||
| expresszívum | nincs | bocsánatkérés, köszönet, gratuláció, felköszöntés, részvét | ||||||||||||
| deklaráció | szó-világ/világ-szó | hadüzenet, kinevezés, házastárssá nyilvánítás | ||||||||||||
"Az emberi hitek nincsenek közvetlenül a cselekvésekhez kötve. Ha nem kombinálják őket megfelelő vágyakkal, az emberi hitek tehetetlenek. És az emberi vágyak szintén tehetetlenek, ha nincsenek megfelelő hitekkel kombinálva. …
Mivel az emberi lények belső reprezentációs rendszerében a kijelentő és a felszólító funkciók szét vannak választva, szükség van újbóli integrálásukra. Ezért az emberek gyakorlati következtetéseket végeznek, a hiteket és a vágyakat újszerű módokon kombinálják, hogy azok először szándékokat, majd cselekvést eredményezzenek."
[RuthM]
"… egy ilyen élmény, a maga intenciójával együtt, jelen lehet a tudatban, anélkül, hogy a tárgy egyáltalán létezne, vagy anélkül, hogy ez a tárgy egyáltalán lehetséges lenne. Ezt a tárgyat véljük, vagyis az ezt a tárgyat vélés az élmény; a tárgy azonban pusztán vélt és valójában semmi." [Edmun]
Ugyancsak fölösleges és félrevezető az elkülönülten, önmagában létező ént vagy tudatot feltételeznünk. Újracsak azt kell mondani ehelyett, hogy az én(tudat) az intencionális élmény egyik komponense, nem független létező."Ám ha úgyszólván benne élünk a kérdéses aktusban, ha egyszerűen feloldódunk például a megjelenő esemény észlelő szemlélésében, vagy a fantázia játékában, egy mese olvasásában, egy matematikai bizonyítás levezetésében stb., akkor a végrehajtott aktusokban egyáltalán nem vesszünk észre egy vonatkozási pont értelmében vett ént. Az én-képzet » készenlétben« állhat, hogy könnyűszerrel előtérbe nyomulhasson, vagy inkább hogy újra megvalósuljon; azonban csak ha valóban megteremtődik, és a vonatkozó aktussal eggyé válik, akkor vonatkozunk mi úgy a tárgyra, hogy az én ilyen fajtájú vonatkozásának valami deskriptíve felmutatható felel meg." [Edmun]
Husserl kifejezésével élve: "az én semmi több, mint a » tudat egysége«". És mindazon túl, hogy nem kell feltételeznünk, pontosabban nem kell figyelembe vennünk sem az önmagában létező tárgyat, sem az elkülönült (én)tudatot, el kell vetnünk azt a nézetet is is, ami az intencionalitást a külvilág leképezéseként modellezi. Ha ugyanis azt feltételeznénk, hogy a külvilág dolgait egy belső reprezentációba képezzük le, és a tudatunk ezt "ismeri fel", akkor végtelen ciklusba kerülnénk, ugyanis fel kéne tenni a kérdést, hogy a belső reprezentációink hogyan állítjuk elő és hogyan észleljük."Ha valaminek a képként való felfogása egy, a tudat számára intencionálisan adott objektumot előfeltételezne, akkor ez nyilvánvalóan végtelen regresszushoz vezetne, mivel maga ez az objektum ismét csak egy kép által konstituálódna;" Hua XIX/1.437. idézi: [Ullma]
A széles körben bevett, de épp ezért félrevezető, nem kívánatos konnotációval rendelkező 'intencionális tárgy' kifejezés helyett Husserl inkább az (intencionális) matéria vagy intencionális anyag terminust használja (ami mellett a továbbiakban a (propozícionális) tartalom kifejezést is használni fogom). Nem lehet elégszer hangsúlyozni, hogy ennek az intencionális tárgynak (vagy intencionális tartalomnak, matériának) a definiálása szempontjából teljesen indifferens annak létezése." … az intencionális tárgy ugyanis a szubjektum prespektívájából megállapított fogalom. Intencionális tárgynak lenni nem más, mint annak a valaminek lenni, amit a szubjektum a 'mi az, amire gondolsz' kérdésre őszintén válaszol." [Tozse]
Fontos az a husserli kritika (és újraértelmezés) is, amely az értelemadással és az intencionális tárgy felfogásával kapcsolatos. Husserl azért tartja fontosnak bevezetni a felfogás(értelem) fogalmát az intencionalitás modelljébe, mert csak így lehet megragadni azt a tényt, hogy az intencionális tartalomra (matériára) irányulásunk mindig valamilyen szempontból, valamilyen apektusból valósul meg. Egy intencionális tartalomra sosem a maga teljességében tekintünk, hanem mindig csak valamilyen szempontból valósul meg az irányultság. És – ahogy ezt már jeleztem korábban – Husserl szerint ez a "részlegesség", ez a valamilyen aspektus szerinti irányultság nem leképzésként, hanem felfogásként, értelemadásként fogható fel inkább. [♦] A nyilvánvaló példa erre az, hogy amikor egy tárgy van előttünk, mondjuk egy asztal, akkor sosem az egészet látjuk, csak valamilyen részét, valamely aspektusát. Az intencionális tartalom mindig csak valamilyen szempont szerint, valamilyen aspektusból, valamilyen – szubjektív – értelemben van jelen az intencionális élményben. Ha egy adott nézőpontból látunk rá elsőként egy asztalra, és az egyik láb takarásban van, így háromlábú asztalként jelenik meg a tudatunkban, mindaddig nem változtatunk ezen az intencionális tartalmunkon, amíg az asztalt körbe járva ki nem derül, hogy annak van egy negyedik lába is. Husserl intencionalitásértelmezésének harmadik fontos összetevője az intencionális kvalitás vagy intencionális minőség kategóriája, bár szerintem ezen a ponton nincs nagy különbség Husserl és Brentano felfogása között. Husserl is fontosnak tartja azt, hogy mindig számba vegyük az intencionális aktus minőségét, akárcsak Brentano. Az intencionális tartalom meghatározza azt, amire az intencionális aktus irányul, míg a kvalitás azt a módot, ahogy ez az irányulás megvalósul. Husserl többször használja érdemben Brentano tipizálását, és nem bírálja fölül azt: fogalmilag "legalul" vannak a képzetek, és ezekre épülnek az ítéleteink, illetve a vágyaink (késztetéseink). Ebben a dimenzióban lehetne finomabb fogalmi felbontást is készíteni, ha a searle-i értelemben vett megfelelési irány fogalma által "kijelölt" felosztáson vagyis a kijelentések és késztetések kettősségén túl figyelembe vennénk további szempontokat. A cselekvések, beszédaktusok sokféle típusa (kérések, parancsok, ajánlatok, remények, aggodalmak stb.) beemelhető lenne a modellünkbe, ha így tennénk, akkor valóban érdemes lenne különböző cselekvési módokról, attitűdökről vagy – a beszédaktus-elmélet által bevezetett – illokúciós erő ilyen-olyan típusairól beszélni, de ezt a részletesebb tipologizálást itt fölöslegesnek tartom, így egyelőre eltekintek ezek modellezésétől. A hiteink, késztetéseink, propozícionális attitűdjeink összefüggő rendszert, sőt kauzális rendszert alkotnak [Altri] Ha Ego úgy vélekedik, hogy kevés benzin van a kocsijában, és tudja, hogy a tervezett útra kevés lenne, akkor tudja azt is, hogy egy benzinkútnál tankolnia kell. A propozícionális attitűdökre (azok kialakulására, változására) hatnak a külvilág tárgyai, az intencionális állapotaink, vélekedéseink "kauzálisan kapcsolódnak a külvilág dolgaihoz, eseményeihez és sajátosságaihoz". Ez már egy második kauzális viszonyrendszert jelent, ami a belső és külső világ "tárgyai" közötti kapcsolatokat jellemzi. A kétfajta kauzális rendszer egy egységet (Altrichter Ferenc kifejezésével élve: "kauzális teret") alkotva folyamatosan "kauzális befolyással" van az Egora. A kauzális hatásrendszer létezésén túl azonban az attitűdjeink további "kényszereknek" vannak alávetve. A propozícionális attitűdjeink világában ugyanis szemantikai, logikai kényszerek is érvényesülnek. A logikai-szemantikai kényszerek létezése és "befolyásolási képessége" azért különösen fontos, mert feltételeznünk kell azt is, hogy a racionalitásnak akár az ideális, akár a reális formáját is vesszük figyelembe, a racionalitásnak erős attitűdbefolyásolási képességet kell tulajdonítanunk. Érdemes is egyfajta zártság elvként megfogalmaznunk a racionális gondolkodásból fakadó logikai kényszereket."A reális eseteknek sokkal jobban megfelel az az elv, amit a hitre vonatkozó zártsági elvnek nevezek. Ez az elv azt mondja ki, hogy a hit zárt a tudott vagy akárcsak elhitt logikai implikáció szempontjából, azaz ha valaki elhisz egy kijelentést, és tudja vagy csupán azt hiszi, hogy a kijelentés logikailag implikál egy másikat, akkor el kell fogadnia a másik kijelentést is. Ennek az elvnek azonban fontos tudatfilozófiai következményei vannak. Tegyük fel, azt hisszük, hogy nem q, és azt is hisszük, hogy p. Ha viszont rájövünk arra, hogy p implikálja q-t, akkor meg kell változtatnunk eredeti mentális állapontunkat q tagadását illetően. A zártság elve arra kényszerít mindannyiunkat, hogy többé ne higyjük el q tagadását, arra tehát, hogy eredeti propozicionális attitüdünket feladjuk. Az interszubjektív racionalitás által kikényszerített ilyen változás nem egyszerűen a mentális tartalom megváltozását jelenti, hanem magának a pszichikus állapotnak a megváltozását. A reális racionalitás regulatív szabálya a logika konstitutív szabályaival összhangban – hogy úgy mondjam – felülbírálja a kauzális tér elemeit, és bizonyos pszichikus állapotokat egyszerűen megsemmisít és kiküszöböl a kauzálisan releváns állapotok köréből." [Altri]
A zártság elve megköveteli az önismeretet. Akkor változtathat valaki az attitűdjein, ha tud róla, hogy korábban milyen intencionális állapotban volt. Ez viszont már másodrendű intencionalitást jelent, hiszen az Egonak tudnia kell, hogy tudott valamit korábban. Olyan fogalmakkal kell tehát bővíteni mind az Ego egyes szám első személyű, mind a megfigyelő harmadik személyű ontológiáját, mint a hit, a vélekedés, vágy, a gondolat. Az önismeret tehát fogalmilag szükséges a modellünk számára, ez viszont megköveteli az öntudatnak, a szelfnek, a szubjektum fogalmának beemelését is, "hogy képesek legyünk önmagunkat a propozícionális attitűdök szubjektumaként felfogni" [Altri] A szigorú fogalmi építkezés logikája csak ezen a ponton engedné meg nekünk, hogy a modellünkbe felvegyük a fokális ágens (Ego), illetve a társas ágens (Alter) fogalmát, és innen indulva lehet a társas preferencia kategóriája alá sorolható olyan fogalmakat is definiálni, mint egoizmus, altruizmus, önfeláldozás stb. (☜) Husserl nyomán óvatosan kell kezelnünk a reprezentáció fogalmát, nehogy a természetes beállítódás által kínált naív elképzelések vagy a pszichologizmus csapdájába essünk, de ez nem jelenti azt, hogy ne lehetne, sőt ne kellene használnunk ezt a kategóriát. Jelentőségét az a puszta tény is mutatja, hogy a terminus sokszorosan túlhasznált, több jelentésrétegeket is el lehet különíteni a fogalomhasználati gyakorlaton belül, ezért nagyon kell vigyázni arra, hogy ne keverjük össze ezeket. Az intencionális aktus értelmezésével kapcsolatban bemutatott eddigi fogalmakat egymáshoz való viszonyukban ábrázolva feltüntetem még a reprezentáció fogalmának fontosabb értelmezési lehetőségeit is.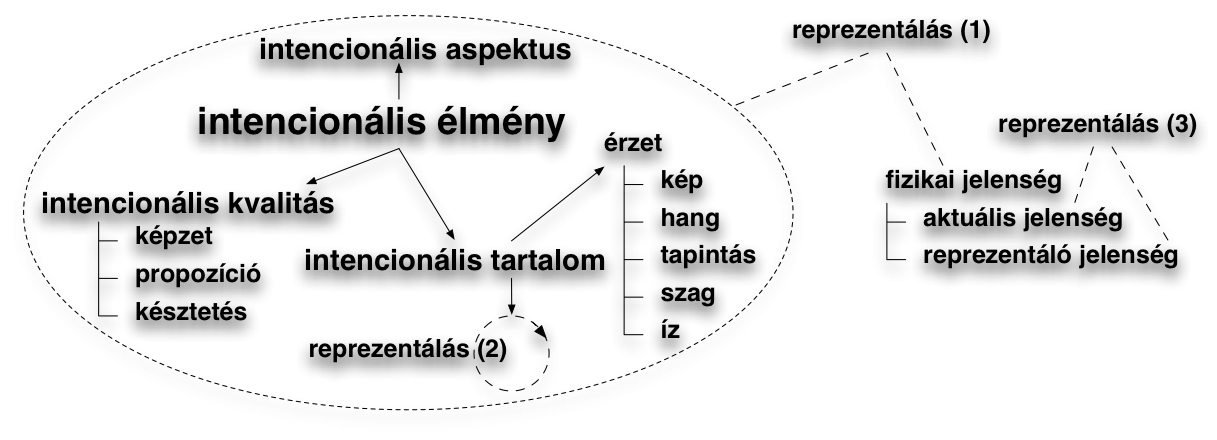
Az intencionális élmény, intencionális aktus egészét jelzi a szaggatott vonallal határolt ellipszis. Az intencionális aktus az érzetadatokon keresztül valamilyen beállítódás mentén irányul az intencionális matériára, tartalomra valamilyen intencionális kvalitással, minőséggel jellemezhető módon. Az intencionális tartalom többféle lehet – az érzetadatoknak típusainak megfelelően. Eközben legalább háromféle reprezentációértelmezésről beszélhetünk. Egyrészt – a husserli intések ellenére – beszélnünk kell valamilyen reprezentációról a valós jelenségek és annak tudati feldolgozása, intencionális irányulása viszonylatában (1). Másrészt a tudat reflexív önmagára irányulása a reprezentáció második szintjét teremti meg (2). Harmadrészt a valós jelenségek, fizikai objektumok világában is teremthetünk a valós jelenségek világán belül maradó reprezentációkat (3). A kulturális tárgyaink, jelenségeink, egy könyv, egy festmény, egy fénykép vagy egy karjelzés, egy visszavonulást jelző harcikürtjelzés – ezek mind példák lehetnek erre. Az intencionalitás modellje segít értelmezni azt a fontos jelenséget, hogy a reprezentációink lehetnek tévesek is. Intencionalitásunk irányulhat nem létező tárgyakra is (például egy szárnyas vizilóra), vagy a vélekedéseink lehet logikai értelemben tévesek (emiatt van szükség az episztemikus és doxasztikus logika elkülönítésére). A kérdés itt az, milyen funkciót tulajdoníthatunk a téves képzeteinknek. Érdemes komolyan vennünk Ruth Millikan megjegyzését ezzel kapcsolatban.
"Ha az igaz hitek funkcionálisak, a hamis hitek pedig legtöbbször nem rosszabbak az üres elménél, akkor még a tévedésre rendkívül hajlamos hitrögzítő eszközök is jobbak lehetnek a hitrögzítő eszközök teljes hiányánál … Mivel rendkívül pontos hitrögzítő eszközök tervezése nehéz, talán valójában előnyösebb túl sok hitet rögzíteni, megengedve, hogy közülük egyesek hamisak lesznek. Ennek megfelelően hitfelhasználó mechanizmusainkat talán arra tervezték gondosan, hogy képesek legyenek tolerálni a hamis hitek magas arányát." [RuthM]
Teleológia
Az intencionalitás, a valamire irányulás fogalmával gyakran összekapcsolják a teleológia fogalmát, amely szűkebb terjedelmű kategória az intencionalitáshoz képest, de mivel sokan és széles körben hivatkoznak rá, ezért fontosnak tartom minél pontosabban tisztázni a jelentését. Azért is szükség van erre, mert világossá kell tenni azt is, hogy mi e fogalom viszonya egy másik kategóriához, a teleonómia fogalmához, amit a biológia használ. Amilyen gyakran hivatkozunk a társadalmi cselekvéseink célkövető, teleologikus jellegére, ugyanolyan gyakran alkalmazzuk a biológiai rendszerek, jelenségek, entitások jellemzésére az olyan fogalmakat, mint a funkcionalitás vagy célszerűség kategóriái. A későbbiekben nagyon fontos lesz, hogy el tudjuk precízen különíteni egymástól a társadalmi és biológiai rendszerekben egyaránt fellelhető funkcionalitás, "célra törekvés" eltérő minőségeit. Amíg a társadalmi cselekvést jellemző célra irányulást a teleologikus, addig a biológiai rendszerekhez rendelhető – az adaptivitásban megnyilvánuló – célszerűséget a teleonomikus jelzővel illethetjük. A teleonómia fogalmát Colin Pittendrigh vezette be 1958-ban. Az ő meghatározását azonban túl tág értelműnek találta Ernst Mayr [Ernst] aki a biológia által vizsgált kétfajta célkövető (end direction) jelenséget elkülönítve egymástól a teleonómia és teleológia fogalmainak párhuzamos használatát javasolta. Mayr azért kritizálta Pittendrigh értelmezését, mert az nem tett különbséget aközött, hogy egyfelől az individuumok (rendszerek) célkövető módon, szándékosan (purposefully) képesek viselkedni, másfelől a genetikai programok evolúciójában vélelmezett – a célszerűség értelmében vett – célra törekvés között [Ernst] Mayr a teleonómia fogalmát így valamely program, információs kód alapján viselkedő individuum, rendszer célkövető minőségére javasolta leszűkíteni. Ebben az értelmezésben a biológia mint tudomány csak a teleonómia jelenségére tud példával szolgálni [Ernst] [Ernst] Hayne Reese a teleológia, illetve teleonómia kategóriakettőst két új fogalomra alapozva állította szembe egymással [Reese] Reese megkülönböztette egymástól a céltudatosság (purposefulness) és a célszerűség (purposiveness) fogalmait egymástól. Céltudatosság fogalma alatt azt értette Reese, hogy az adott viselkedésnek, működésnek, entitásnak van valamilyen belső meghatározottsága, míg a célszerűség minőségét arra az esetre javasolta alkalmazni, amikor az adott viselkedés, működés, entitás valamilyen – hasznos – funkciót szolgál. Abban a kérdésben, hogy miként lehet a "valamely program, információs kód" alapján történő viselkedést pontosabban leírni, a funkció fogalmát hívhatjuk segítségül [Larry] [RuthG] amit Larry Wright vagy Ruth Millikan felfogásával szemben én a teleonómia fogalma alá gondolok besorolhatónak. Bár Wright és Millikam funkcióértelmezése nem egyezik meg, azért pár közös vonást találhatunk az elméletükben [Forra] Az F funkció (működés, tevékenység) akkor és csak akkor egy X entitás funkciója (működése, tevékenysége), ha teljesül az alábbi két feltétel: (i) X egy korábbi Y entitás reprodukciója, amely korábban F-t csinálta, illetve (ii) X azért reprodukálódott, mert Y korában F-t csinálta. Ehhez szerintem érdemes még hozzávenni azt a feltételt is, hogy F egy olyan oksági láncon keresztül jött létre, amit valamilyen – a természet vagy az ember által létrehozott – kód váltott ki. Mindezt pedig az alábbi formulával fejezhetjük ki.$\concept{TELEONOMIC\_STATEMENT}\defi ((Y(t_1) \rightarrow F)\rightarrow (X(t_2) \rightarrow F)) \land (t_1 < t_2) \land X(t_1)\in R \land Y(t_2)\in R$
teleonomikus állítás (hun) – teleonomic statement (eng)
ahol R egy olyan reprodukciós osztály, amelynek tagjai mind megvalósítják az F funkciót, R-be tartozik mind az X, mind az Y entitás, és $X(t_1)$ időben megelőzi $Y(t_2)$-t. Nagyon fontos kiemelni, hogy a teleonómia funkció fogalmában van egyfajta meghatározottság, determinizmus, ami a teleológia fogalmából hiányzik. Amikor Ronald de Sousa a teleologikus gondolkodás, beállítódás sajátosságát akarta kifejezni, a teleologikus állítás formuláját az oksági állítás formulájához hasonlította [Ronal] Amíg az oksági állítás formulája egy egyszerű kondicionálissal kifejezhető ($A \rightarrow B$), addig a teleologikus állítás leírásához bonyolultabb képletre van szükségünk. A teleologikus cselekvést leíró formula "középpontjában" a G cél (goal) áll, az a jövőbeni állapotot, amit az ágens szeretne elérni a cselekvésén keresztül. A cél eléréshez szükséges valamilyen M eszköz (mean), és – ezt Sousa nem vette figyelembe, én teszem hozzá a modellhez – számolni kell a cél megvalósulásakor jelentkező C következménnyel (consequence). Ezekkel a paraméterekkel a teleologikus állítást a következőképpen írhatjuk le.$\concept{TELEOLOGIC\_STATEMENT}\defi (M \rightarrow (G\to C))\rightarrow M$
teleologikus állítás (hun) – teleologic statement (eng)
A formula három egymásba ágyazott kondicionálisból áll. A legfontosabb kondicionális azt írja le, hogy ha egy M cselekvést megvalósítok, akkor elérem a G célt. Ha ezt a kondicionálist mint egy egész állítást teszem meg egy második kondicionális előtagjává, akkor abból a cél elérését remélhetem, ezért kerül a második kondicionális utótagjába a G. Végül számolnom kell azzal is, hogy a céloknak lehetnek következményeik, vagyis ha a G cél megvalósul, akkor a C következmény is létrejön (ezt fejezi ki a harmadik, a formula közepébe beágyazott kondicionális).Késztetés, vágy, érték
Az intencionalitás egyik kvalitása a késztetés. Ezt a fogalmat tartom a legáltalánosabbnak, amit fogalmi primitívként érdemes felvenni a modellbe, és amiből levezethetünk olyan további fontos fogalmakat, mint a vágy, az érték, szükséglet, cél vagy a szándék. A szükséglet jelentését itt azonosnak minősítem a késztetés fogalmának tartalmával, így a két terminust egymás szinonímáinak tartom. A továbbiakban a késztetés, vágy és érték fogalmai közti kapcsolatot szeretném tisztázni. Természetesen nagyon nehéz vagy talán nem is lehet tisztán elkülöníteni egymástól ezeket a fogalmakat. Régóta és gyakran használjuk őket, rengeteg jelentésréteg tapadt rájuk, a különböző kontextusokban részben változó és sokszor egymást átfedő jelentéseket adunk nekik. Azért érdemes a késztetés kategóriáját alapul venni, mert ez tűnik a legáltalánosabb jelentésűnek, ami még nem "követeli meg" feltétlenül a tudatosság jelenlétét. A vágyhoz vagy az értékhez – értelmezésem szerint – mindig érdemes valamilyen szintű tudatosságot rendelnünk, így ezeket speciálisabb fogalomnak kell tartanunk. A késztetéseknek (vágyaknak, értékeknek) mindig van polaritása, amit a – fizikai világból ismert – vonzás és taszítás analógiájára hivatkozva ragadhatunk meg. Ezt az analógiát arra is használhatjuk, hogy jelezzük vele a késztetések (vágyak, értékek) energetizáló képességét, szerepét. A késztetés kifejezés maga szépen kifejezi ezen intencionális kvalitás meghatározó vonását, ti. azt, hogy a késztetés (vágy, érték) cselekvésre késztet. A késztetések polaritását magyar nyelvi terminusokkal nem tudjuk kifejezni, de a vágyak szintjén már megtalálhatjuk ezt a kettősséget a terminusok között, amikor – ellentétes polaritású – vágyakról és averziókról beszélünk. Ha a vágyat mint vonzást eredményező, pozitív késztetést, míg az averziót mint taszítást eredményező, negatív késztetést gondoljuk el, akkor már azt a megkülönböztetést származtathatjuk mind a késztetések, mind az értékek felé. Mondhatjuk, hogy a késztetéseink lehetnek pozitív, illetve negatív polaritásúak, vagyis vonzódás, illetve taszítást eredményező intencionális kvalitások. Az energetizálási analógia alapján mondhatjuk még azt is, hogy a két pólushoz mindig kapcsolódik a kielégülés, illetve a kielégületlenség (frusztráció) jelensége, állapota. Azt a kérdést, hogy vannak-e és ha igen, milyen alapvető késztetései (szükségletei) vannak az embernek, itt nem tárgyalom, még akkor sem, ha egyébként a gyakorlati szempontokra figyelő cselekvéselméleti modell számára megkerülhetetlen kérdésnek tartom. A modellépítés következő kérdése az, hogy mit is jelent a vágy fogalma. Értelmezésem szerint a vágy a tudatba került pozitív (polaritású) késztetés. És természetesen a vágy ellentéte, az averzió a tudatba került negatív (polaritású) késztetés. A vágy/averzió tehát úgy működik, hogy az elme részben a biológiailag adott, részben az egyén története során szerzett, tanult késztetéseket elraktározza, és ezek egy része a külső ingerek hatására valamilyen belső – a személyiségre jellemző – dinamika szerint eléri a tudatosság szintjét. Amíg a késztetésekről van csak szó, addig a tudattalanban levő diszpozíciókról beszélhetünk, és amint ezek közül valami tudatossá válik, akkor jelenik meg bennünk a vágyakozó irányultság valamire (vagy a valamitől való averzió). A tudatosságnak egy következő szintjét is figyelembe kell vennünk ahhoz, hogy modellezni tudjuk az érték jelenségét. Az értéket én másodrendű vágynak tartom, ami voltaképp a tudatba került késztetések közti tudatos választással, elköteleződéssel azonosítható. A késztetéshez hasonlóan és a vágytól eltérően az érték diszpozicionális jellegű. A másodrendű vágyfogalmakkal kapcsolatos elképzeléseket röviden bemutatom a fejezet későbbi részében. A vágyak és a célok, akaratok, szándékok közti kapcsolatra viszont csak egy későbbi fejezetben fogok kitérni (☜) itt tehát nem foglalkozom ezzel a kérdéssel. Még ebben a bevezetőben kell azonban megválaszolnom azt a kérdést, hogy mi a vágy és a preferencia fogalma közt a kapcsolat. Egyrészt fontos hangsúlyoznom, hogy a preferencia is a tudatos jelenségek közé tartozik. Ez a tétel azon az alapon védhető, ha arra hivatkozom, hogy ha a preferenciarendezés két (vagy több) alternatív összehasonlításának műveletét jelenti, akkor ebben látnunk kell a tudatos mérlegelés jelenségét. A preferenciákat így nem a késztetések, hanem legalább a vágyak szintjén kell elhelyeznünk. Mivel később beszélni fogok másodrendű preferenciákról is, ezért a preferenciákat mind a vágyak, mind az értékek fogalmával kapcsolatba hozhatónak gondolom. Mindezt figyelembe véve a preferenciát én a vágyak (vagy a preferenciák) közti választásnak vélem elgondolhatónak. Ezt megfordítva mondhatjuk azt is, hogy a vágy (averzió) valamelyik irányú reifikált preferencia (☜) vagyis a preferenciarendezésbe vont, és az összehasonlítás ereményeként preferált vagy diszpreferált elemekre való irányulás.Diszkrepancia alapú vágyelmélet
Charles B. Cross a diszkrepancia fogalmára alapozott vágyelméletet írt le modális logika segítségével [Charl] A diszkrepancia fogalma azért került az elmélet központjába, mert az ember vágyai, majd az ezekből fakadó szándékai, majd az ezek eredményeként megvalósuló cselekvései azokból az eltérésekből, diszkrepanciákból magyarázhatók meg, amelyek az ember által célul kitűzött, jövőbeli és a jelenbeli, ténylegesen létező állapotok közti léteznek. Ha a most is létező és a célul kitűzött állapotok nem különböznének egymástól, akkor nem beszélhetünk diszkrepanciáról köztük, de nem beszélhetünk vágyról, sőt, tulajdonképpen célról sem. Mielőtt a logika bemutatásába kezdenénk, nézzünk meg egy példát, amin keresztül be lehet vezetni az alapfogalmakat is. Vegyük a lehetséges jelen- és jövőbeni világállapotokat, és az ezeket leíró propozíciókat jelöljük $A,B,C,D$ betűkkel. Ha egy állapot fennáll, akkor a rá vonatkozó A propozíció igaz, ha az állapot nem áll fent, akkor a propozíció hamis: $\lnot A$. Az állapotok közül emeljünk ki két típust: G jelölje azt az állapotot, amit a cselekvő szeretne elérni, vagyis legyen G a cselekvő célja (goal), B pedig jelölje a cselekvő vélekedését (belief) a világ éppen adott helyzetéről. [♦] Az ágens célja és hite is állhat több – igaz vagy hamis – propozícióból. Cross példája egy ágensről és annak négy macskájáról szól. Ha az ágens csak akkor megy el otthonról, amikor már biztos benne, hogy mind a négy macskája bent van a házában, akkor a célállapotként rögzíthetjük a következőt. ahol $E,B,S,C$ rendre azt jelöli, hogy az E(lza), B(erci), S(aci), C(irmi) nevű macska bent van a házban. Induljunk ki abból a helyzetből, amikor az ágens annyit tud, hogy Elza és Berci nincs a házban, míg Cirmi ott van, viszont nem tud semmit arról, vajon Saci bent van-e vagy sem. Ezt jelöljük a kezdőállapotnak. Mit kell tennie emberünknek, hogy elérje célját vagyis a célállapotba kerüljön? Egyfelől meg kell keresnie Elzát és Bercit, és be kell vinnie őket a házba, másfelől meg kell győződnie arról, hogy Saci bent van-e a házban. Ha Sacit megtalálja odabent, akkor vele nem kell többet tennie, egy lépéssel közelebb került célja megvalósulásához. Ha viszont Saci nincs a házban, akkor az ágensünknek vele is ugyanazt kell csinálnia, mint a másik két kint kóborló macskával: megkeresni, behozni őket. Ezt a két opciót kétféleképpen kell kezelni, kétféleképpen is érdemes megnevezni őket mint a diszkrepancia két típusát. A célok és hitek közti diszkrepancia (goal/belief discrepancy) két típusa az inkompatibilitás és a nem-teljesség. Az összeférhetetlenség, inkompatibilitás (incompatibility) fogalmával azt a helyzetet jelölhetjük, amikor a G célállapot és az $B_i$ aktuális állapotról tudja az ágens, hogy valamely pontban, valamilyen mértékig nem nem egyezik meg. Példánkban ágensünk azon hite (tudása), hogy Elza és Berci biztosan nincs a házban, a célhoz képest kifejezhető inkompatibilitásnak felel meg. Ezzel szemben a hiányosság, nem-teljesség (incompleteness) fogalmával írhatjuk le azt a helyzetet, hogy a negyedik macskáról, Cirmiről nem tud semmit az ágens. Inkompatibilitás esetén az ágens késztetése (vágya) az lesz, hogy megváltoztassa a célhoz képest eltérő állapotokat, vagy másként: a célállapotba hozza őket. Ehhez képest a hiányosság esetén – részben – más a teendő, hiszen első lépésként információt kell gyűjteni, meg kell szüntetni a tudáshiányos állapotot, majd a beszerzett új információ alapján vagy cselekedni kell (amit megint a cél- és aktuális állapot közti eltérés megszüntetésének vágya hajt) vagy nem kell semmit sem tenni (ha az derül ki a beszerzett információból, hogy nincs diszkrepancia). De kövessük tovább Cross példáját. Mi történik akkor, ha a gazda megtalálja odakint Elzát és behozza a házba? Megváltozik az aktuális állapot, amivel kicsivel közelebb kerülünk a célhoz. Jelöljük ezt egy újabb formulával. Tegyük fel azt, hogy ezután az ágens felfedezi Sacit az ágy alatt, tehát már tudja, hogy Saci a házban van. Ebben az esetben megszűnik a hiányosság értelemében vett diszkrepancia a cél- és aktuális állapotok között, de még megmarad az összeférhetetlenség. Az újabb állapot a következőképpen jelölhetünk. Ekkor már csak egyetlen cica van odakint, Berci. Ha a gazda a keresésére indulna, és közben észlelné, hogy Cirmi ott áll a főbejáratnál arra várva, hogy a gazda kinyissa az ajtó, és ő kiszaladhasson rajta, akkor az ágens dönthet úgy, hogy a hátsóajtón át indul Berci felkutatására, hogy megakadályozza Cirmi kiszökését. Ezt a "csavart" Cross azért tette bele a történetébe, hogy erre hivatkozva később el tudja különíteni a diszkrepanciák két fontos szerepét, funkcióját. De most még maradjunk a macskás sztorinál, fejezzük be, már csak egy lépés van hátra. Ha ugyanis a gazda a kertben megtalálja a negyedik macskát és behozza a házba, akkor ezzel olyan állapot áll elő, ami összehangba kerül az eredeti céllal. Ha ugyanis Bercit is behozta a gazda, akkor ezzel megint új állapot keletkezett. Ez a $B_3$ állapot viszont minden összetevőjében megegyezik a G célállapottal, tehát kijelenthetjük, hogy az ágens elérte célját. És a bemutatott történet alapján már rámutathatunk arra is, hogy Cross hogyan javasolta elkülöníteni a cél/hit-diszkrepancia két szerepét, funkcióját egymástól. Szerinte a diszkrepancia lehet:- a)] valami, amit egy racionális ágens megpróbál megszüntetni;
- b)] valami, amit egy racionális ágens megpróbál nem létrehozni.
| az ágens | az eset neve | jele | szükséges cselekvés | |||||||||||
| vágyja $A$-t és véli $A$-t | egyezés | $\oplus A$ | nincs, mert beteljesült a vágy | |||||||||||
| vágyja $A$-t és véli $\lnot A$-t | összeférhetetlenség | $\bigtriangleup A$ | előidézni $A$-t | |||||||||||
| vágyja $A$-t, nem tudja, $A$ vagy $\lnot A$ | hiányosság | $\bigtriangledown A$ | megtudni, hogy $A$ vagy $\lnot A$ | |||||||||||
| nem vágyja sem $A$-t, sem $\lnot A$-t | közömbösség | $\lnot A$ | nincs, mert nincs vágy | |||||||||||
"(1) S M-t kizárólag az E-re irányuló vágya eszközeként akarja akkor és csak akkor, ha (a) S akarja M-t, (b) S akarja E-t és (c) S csak azért akarja M-t, mert úgy hiszi, hogy M elérésével elősegíti (promotálja) E elérését." [Ellio]
A meghatározásban szereplő rövidítések az S szubjektumra, az M eszközvágyakra, az E célvágyakra vonatkoznak. További erőssége még Sober és Wilson elméletének az, hogy a vágyfogalmakra támaszkodva két tézist is kimondanak, amelyek – bizonyos értelemben – a vágyakkal kapcsolatos előrejelzéseknek is tekinthetők. Íme a két tétel.
"(2) ha S csak mint E elérésének eszközeként vágyik M-re, akkor ha S arra a belátásra jut, hogy M nem biztosítja E elérését, akkor S M-re irányuló vágya elmúlik, de továbbra is akarja E-t és megpróbál találni új eszközöket E eléréséhez."
[Ellio]
"(3) Ha S csak mint E elérésének eszközeként vágyik M-re, akkor ha S eléri E-t, de nem éri el M-t (pontosabban: ha S azt hiszi, hogy ez nem történt meg), akkor S nem vágyik többé M-re; azonban ha S eléri M-t, de nem éri el E-t, akkor S tovább vágyik E-re."
[Ellio]
Másodrendű vágy: érték
Egyszer, amikor Diogenész Kraneioszban sütkérezett a napon, Nagy Sándor kíséretével épp arra haladva megállt előtte és azt mondta neki: – Kérj tőlem, amit akarsz! – mire Diogenész csak annyit felelt – Ne álld el előlem a napot! Évezredekkel később az amerikai Clay Intézet hét, régóta ismert matematikai probléma megoldásának ösztönzésére megalapította a Millennium-díjat. Bármelyik probléma megoldásáért egy-egymillió dollárt ajánlottak fel. Grigorij Perelman, orosz matematikus 2002-ben egy weboldalon közzétette a megoldást, amit a szakma idővel érvényesnek minősített, ezért 2010-ben a Clay Intézet felajánlotta Perelman számára a Millennium-díjat és a vele járó egymillió dollárt. Perelman nem fogadta el egyiket sem. – A díj teljesen irreleváns számomra. – nyilatkozta – Ha a bizonyítás jó, nincs szükség külön elismerésre. [index] Két történet, amelyekhez többféleképpen viszonyulhatunk. Többen lehetnek azok, akik értetlenkednének a történetek hallatán, de talán akadnak olyanok is, akik szeretnének a főszereplők helyében lenni. Akik szeretnének olyanok lenni, mint ők. Akik vágynak arra, hogy úgy ne vágyjanak a földi hívságokra, ahogy azt Diogenész vagy Perelman tette mintázta. Bármennyire is ritka, szinte életidegen a két példa, pont a szokatlansága miatt alkalmas arra, hogy segítségükkel könnyebben felismerhessük azt a nagyon fontos összetevőt, ami a két meséről szóló viszonyulásban közös, és amit megtalálhatunk sok más történetmesélésben is. Amikor erkölcsi tanulságokat fogalmazunk meg egy történet kapcsán, akkor a szereplők cselekvéseire, illetve az azok mögött meghúzódó vágyakra, késztetésekre vonatkozóan fejezzük ki az értékeléseinket. De mit is jelent ez az értékelés? Azt a vágyat (vagy averziót), amit a történetben szereplők cselekvéseivel, késztetéseivel (vágyaival vagy averzióival) kapcsolatban érzünk magunkban, és erre az érzésre a tudatunk reflektál valahogyan. Amikor erről van szó, akkor azt kell mondanunk, hogy a történetek értékelésekor másodrendű vágyak (averziók) dolgoznak bennünk, hiszen ilyenkor a történetekben levő késztetésekre irányuló késztetésekről kell beszélnünk. A késztetésekkel kapcsolatos másodrendű fogalmakat Harry Frankfurt és Richard Jeffrey emelte be a tudományos diskurzusba a hetvenes években. [♦] Frankfurt a másodrendű vágy és a másodrendű akarat fogalmára építette fel a személyiség fogalmának meghatározását, amit ő az ember legfőbb sajátosságának tekintett [Harry] míg Jeffrey bevezette a másodlagos preferencia fogalmát [jeffr] amit a döntéselmélet keretein belül alkalmazott [jeffr] Frankfurthoz és Jeffreyhez képest David Lewis annyiban továbblépett, hogy egy, az ember értelmezése szempontjából kulcsfontosságú kategóriát úgy definiált, hogy azt a másodrendű vágy fogalmával azonosította [Micha] Lewis felfogása szerint az érték nem más, mint vágyra vonatkozó vágy, vagyis az értékeink a másodrendű vágyaink. A frankfurti, jeffrey-i nézeteket szélesebb, a lewisi elképzelést szűkebb körben felkapták a vágyakkal, értékekkel foglalkozó diskurzuson belül. Charles Taylor a szelf, az identitás fogalmának meghatározásakor például Frankfurt másodrendű vágy és a különböző értékeléstípusok fogalmaira támaszkodik [Charl] Amartya Sen is egyetértőleg utal a másodrendű preferencia (vagy ahogy ő nevezi: a metapreferencia) fogalmára miközben hivatkozik Frankfurt, Jeffrey elméleteire [Amart] ahogy Albert O. Hirschman is úgy ír kétféle preferenciaváltozásról egy cikkében, hogy közben utal Frankfurtékra [Alber] Vannak persze olyanok is, akik kritizálják a másodrendű vágyfogalmak használatát. Gilbert Harman egy írásában áttekinti Harry Frankfurt, David Lewis és David Copp [CoppD] javaslatait a másodrendű vágyak értelmezési lehetőségeiről, és mindegyik nézetet elutasítja [Gilbe] A Frankfurt-recepció elsősorban a személyiség, a szabad akarat, a felelősség problémája köré épült fel, de ez a témakör a most tárgyalt szempontból nem igazán érdekes. Jeffrey másodrendű preferencia fogalma már sokkal inkább a mostani gondolatmenetbe illeszthető, bár csak akkor, ha pontosabban reflektálunk a másodrendű preferencia fogalmában meghúzódó lényegi mozzanatra. Hogy érthető legyen, mire gondolok, idézek egy rövid – más témakörben mozgó, és önmagában nagyon értékes – szövegrészt a politikai cselekvések logikájáról." … a politikai cselekvés különbözni látszik a magánfogyasztók és termelők piaci viselkedésétől. Amellett is érvelhetünk, hogy a politikai cselekvés természeténél fogva publikus, abban az alapvető értelemben, hogy nemcsak egyéni nyereményeken alapul, hanem a világ lehetséges jövőbeli állapotaira értelmezett preferenciákon, amelyek magukban foglalhatják mások nyereményeit, valamint szabályokra és intézményekre vonatkozó preferenciákon, amelyek garantálhatják ezeket a nyereményeket." [Csont]
Mivel sem az idézet, sem az azt tartalmazó írás egésze nem a preferenciákról szól elsődlegesen, ezért nem kritikát fogalmazok meg vele szemben, csak mint szemléltetésre alkalmas szövegként használom arra, hogy rámutathassak, hogy a szövegrészben reflektálatlanul használt másodrendű preferencia fogalom létezésére. Amikor mások nyereményeiről van szó, akkor azok nyilvánvalóan kapcsolatba hozhatók mások preferenciáival, ezért a fenti idézetben leírt politikai cselekvéseket úgy lehet értelmezni, mint mások preferenciáival (nyereményeivel) kapcsolatos preferenciákat, melyek így más másodlagosak. Ahhoz, hogy megértsük, mit jelentenek és hogyan működnek a másodrendű vágyak, az értékek bennünk, abból kell kiindulnunk, hogy a vágyaink a tudatba került belső és elsődleges késztetéseink (vagy kicsit pongyolábban elsődleges preferenciáink). Ameddig még csak arról van szó, hogy a vágyaink megjelennek a tudatunkban, addig még nyugodtan mondhatjuk, hogy ezek reflexió előtti (prereflektív) intencionalitások. Az elsődleges vágyaink, preferenciáink nem mérlegelések, nem tudatos döntések eredményei, hanem a bennünk levő – részben biológiailag örökölt, részben életünk során tanult, elraktározott – késztetések megnyilvánulásai a környezetünk ingerei adott válaszokként. Nagyon sok esetben kerülünk olyan esetbe, amikor nem egy, hanem több és többféle késztetés, vágy, preferencia jelenik meg egy időben a tudatosság szintjén. Ilyenkor ezek – kisebb-nagyobb – konfliktusba kerül(het)nek egymással, és az ilyen ellentmondásokat a tudatos reflexió, a tudat mérlegelő tevékenysége oldhatja meg (próbálhatja feloldani). A cselekvést tehát nagyon sok esetben nem pusztán a vágyak vezérlik, hanem az egyszerre ható vágyak (és averziók) együttese, valamint az ezekre reflektáló tudat kognitív megfontolásai. Ha pedig így értelmezzük a mérlegelés, a reflexió és a vágyak kapcsolatát, akkor lehet igazán megérteni (és elfogadni), miért javasolta David Lewis, hogy az érték fogalmát definiáljuk úgy, mint a vágyra vonatkozó vágyat. Amikor a vágyak (preferenciák) konfliktusba kerülnek a tudat szintjén, akkor maguk a vágyak válnak (pontosabban azok is) a mérlegelés tárgyává. Amikor a versengő vágyaink között mérlegelünk, amikor reflektálunk rájuk, akkor arról döntünk, hogy melyik vágyunkat soroljuk előbbre a többinél. Ez ugyanúgy egyfajta preferencia kifejezését, mégpedig az aktuális vágyak közti preferencia (vágy) vagy másként az aktuális vágyak közti prioritás kifejezését jelenti. A másodrendű vágy (preferencia) tehát mindig reflektált vágy (preferencia) is egyben. És ez – David Lewis-szal egyetértve – valóban megfelel az érték fogalom tartalmának.Vélekedés, vágy, szándék
A társadalmi cselekvés meghatározó minősége az intencionalitás, ez utóbbi kifejezést azonban könnyű összetéveszteni az intenció fogalmával, sokan és sokszor egymással felcserélhető módon használják a két terminust. Pedig az intenció mint szándék az intencionáltságnak csak egy típusa, és vigyázni kell arra, hogy a két terminus alaki közelsége nehogy áthallásokat, fölösleges és szándékolatlan konnotációkat teremtsen."Az intencionalitás meglehetősen balszerencsés szóalkotás, és mint annyi más szerencsétlen szót a filozófiában, ezt is a németül beszélő filozófusoknak köszönhetjük. A szó arra utal, hogy az intencionalitás az irányítottság értelmében valamiféle kapcsolatban áll a 'szándékkal', olyan értelemben például, hogy ma este moziba szándékozom menni. (A német nyelvben ez nem okoz problémát, mert az Intentionalität másképp hangzik, mint az Absicht, a mozilátogatás szándékának hétköznapi értelmében vett szándék.) Úgyhogy ne feledjük, az angolban a szándék csupán az intencionalitás számos formájának az egyike." [searl]
Searle figyelmeztetése természetesen nemcsak az angol esetében érvényes, a magyarban (és még nyilván sok más nyelvben) ugyanúgy megszívlelendő. Ennek a searle-i kritikának persze nem volt sem azonnali, sem széleskörű hatása. G.E.M. Anscombenak az intencionális emberi cselekvés elemzésében mérföldkőnek számító, Intention című könyvére nem is lehetett hatással, mivel ez a könyv 1957-ben jelent meg először [G.E.M] Searle kritikája ettől még vonatkoztatható lenne Anscombe írására is, mert a könyv az intencionális cselekvés értelmezését célul tűzve az 'intenció' fogalmát az intencionalitás mint szándék jelentés mellett, tehát az intencionalitás egyik típusaként fogta fel. [♦] Ez a "pongyolaság" azonban itt nem zavaró. Anscombe egy kérdéssel indítja értekezését."Egy ember azt mondja, 'Sétálni fogok', és mi azt mondjuk erre, 'ez egy szándék kifejezése volt, nem egy előrejelzés'. De honnan tudjuk ezt?" [G.E.M]
Megijedni, reszketni, összerezzenni, zihálni – ezek nem intencionális jelenségek vagyis nem cselekvések. Elmosogatni, olvasni, taxit hívni – ezek intencionális jelenségek vagyis cselekvések. Anscombe ezzel a szembeállítással kezdve rögtön a könyve elején olyan erős állításokat tesz, amelyeket azóta is sokan és sokat vitatnak a cselekvés filozófiájával kapcsolatos fejtegetésekben. Anscombe szerint az előrejelzésekhez, predikciókhoz tényeket, bizonyítékokat (evidence) rendelünk, okokat (causes) keresünk, az intenciókhoz, szándékokhoz cselekvésre vonatkozó indokokat (reason), és szerinte mindennek lehet oka, de csak az intenciónak lehet indoka. Ebből következően az intencionális cselekvések leírásához, megértéséhez mindig indokakat kell keresnünk és találnunk. Anscombe szerint szándékolt cselekvések azok, amelyekre értelmesen feltehető a – bizonyos értelemben vett – 'miért' kérdés. Ha pedig ez a kérdés értelmesen feltehető, akkor a rá adott választ minősíthetjük a cselekvés szándékának. Nyilván tisztáznunk kell, hogy mit jelent ez a "bizonyos értelemben feltett » miért«" kérdés. Anscombe ezt több lépésben fejti ki. Először azt rögzíti, hogy milyen értelemben nem használható (mert nem nem tehető fel) a 'miért' kérdés. Ehhez két fogalmi dimenzióban elkülöníti az akaratlagos, illetve nem-akaratlagos tudást egyfelől, valamint a megfigyelés által ismert, illetve a megfigyelés nélkül tudott dolgokat másfelől. Az első szempont szerint vizsgálva a cselekvéseinket, Anscombe – egy nagyon termékenynek bizonyult gondolatként – felveti, hogy a cselekvéseinkre többféle leírást is adhatunk, és a cselekvés mindig valamely leírás szerinti cselekvést jelent (acting under a description), míg a többi leírás szerint nem számít cselekvésnek. [♦] A cselekvések leírásaival kapcsolatos diskurzus egyik kedvenc példáját idézve: amikor a mutatóujjammal felfelé mozdítom a villanykapcsoló billenőlapját (1), akkor felkapcsolom a lámpát (2), amivel fényt csinálok a szobában, hogy olvasni tudjak (3). De ezeken túl elképzelhetők más értelmezések is: például az, hogy a lámpakapcsolással jelzést adok valakinek (4), vagy – villanyszerelőként – egyszerűen csak ellenőrzöm, hogy jól kötöttem-e be a kapcsolót (5). Mindegyik leírás egy-egy lehetséges és adekvát leírása, értelmezése lehet annak, amit tettem, a kérdés, hogyan tudhatunk meg többet erről. [♦] (☜) Ez azért fontos, mert ha megkérdezik tőlem a negyedik leírás alapján, hogy miért adtam fényjelzést a lámpa felkapcsolásával, akkor erre felelhetem azt, hogy nem tudtam, hogy ezt teszem. Ilyen esetben nyilván kizárhatjuk azt, hogy az adott leírás mentén szándékolt cselekvésről lenne szó. A szándékom az volt, hogy fényt csináljak a szobában azért, hogy lássak, de nem volt szándékom, hogy valakinek jelzést adjak ezzel, és ha nem akartam ezt, akkor nem is tudhattam erről. [♦] Ha valamiről nem tudok, akkor az nem lehet akaratlagos, akkor az arra vonatkozó 'miért' kérdésre nem válaszolhatok értelmesen, tehát nem minősíthetjük szándékoltnak azt a cselekvés(leírás)t. Megfordíthatjuk azonban a dolgot. Mondhatjuk egyszerűen azt is, hogy nem akartam valamit megtenni (például jelzést leadni a lámpával). Ehhez persze az szükséges, hogy meg tudjuk különböztetni az akaratlagos (voluntary), illetve nem akaratlagos (involuntary) cselekvéseket egymástól. Ezen a ponton azonban megfontoltnak kell lennünk, mert könnyen beleeshetünk az üres, önmagában forgó érvelés csapdájába (ha azt keressük, mi az, ami nem szándékolt, akkor nem felelhetünk azzal rá, ahogy mindaz, ami nem akaratlagos). A megoldás kereséséhez Anscombe javasolja, hogy vizsgáljunk meg néhány példamondatot, amelyek cselekvések leírásaként tekinthetők [G.E.M]| 1) | A belünk perisztaltikus, összehúzódó mozgása. | |||||||||||||
| 2) | Az a furcsa rándulás, rángás, amit olykor az ember teste végez elalvás során. | |||||||||||||
| 3) | "Önkéntelenül hátrahőkölve visszahúzta a kezét." | |||||||||||||
| 4) | "Az a nem tervezett haszon, amelyhez egy ártó szándékú ütéssel jutottam." | |||||||||||||
- megfigyelés nélkül tudja, hogy $A$-t teszi, illetve
- megfigyelés nélkül tudja, hogy $A$ megtételének mi az (ind)oka.
Anscombe intenciófelfogása az oksághoz való viszonyában nem volt egyedi, sőt, inkább azt kell mondanunk, hogy sokak, talán a kor nézetét visszhangozta.
"Wittgenstein, Anscombe és Ryle érveinek hatására egészen a hatvanas évek végéig az volt az általánosan elismert álláspont, hogy, mivel a szándéktulajdonítás és a cselekvés leírása konceptuálisan nem független egymástól, az intenciók nem lehetnek a cselekvés (hume-i) okai. A konceptuális kapcsolat érvét azonban D. Davidson … meggyőzően cáfolta." [huora]
A cselekvést illetően az ok és indok megkülönböztetésével foglalkozva Donald Davidson 'Actions, Reasons, and Causes' című tanulmányában (angolul: [Donal] magyarul: [Donal] az indokot az ok egyik fajtájaként értelmezte. Ebben szembe ment G. Ryle, G.E.M. Anscombe, G.H. von Wright nézetével, akik megkülönböztették a cselekvések gyakorlati indokait az események okaitól – nagyjából azon az alapon, hogy egyfelől a cselekvésekhez szükséges intencionális állapotok nem események, és az okságot események között állapíthatjuk meg, másfelől az indokokra nem találhatjuk meg az okokra jellemző általános törvényszerűséget, nomologikus minőséget. Ez fordulat persze nem kizárólag Donald Davidson nevéhez köthető, szerepet játszott ebben John Searle, Michael E. Bratman is."Az az okság-értelmezés ugyanis, amely az intencionális események és állapotok kettős, logikai-fiziológiai természetét egyetlen kauzalitás-fogalommal képes megragadni, áthidalhatja a test-tudat probléma dualista és monista megközelítései között húzódó szakadékot, s ezáltal új tartalommal töltheti meg magát a problémát is. Ennek a sajátos, dualista-monista konszenzusnak a lényege pedig az, hogy bár minden egyes intencionális esemény és állapot azonos egy fizikaival, logikai jellemzőik meghatározása mégsem természettudományos perspektívából történik. Azaz a kauzalitás-problematikára vetítve ez azt jelenti, hogy jóllehet minden egyes intencionális oknak és okozatnak megfelel egy fizikai jelenség, a közöttük fönnálló viszonyok nem testesítenek meg egyetemes törvényszerűségeket. Az intencionális események és állapotok közötti oksági relációk logikai jellemzői ugyanis mindig valamilyen individuális kognitív háttérre vezethetők vissza. … Az intencionális eseményeknek és állapotoknak ezt a kettős vonását, a kauzális függést és a nomologikus függetlenséget együttesen megvilágító és Davidson által » szabálytalan« monizmusnak nevezett fölfogás tehát egy sajátos, » intencionalizált okság-fogalomra épül." [Szcsi]
Az okság problémakörét a filozófusokra hagyva nem akarok itt azzal a kérdéssel foglalkozni, hogyan kell a cselekvési indokokat érteleznünk. Anscombe elválasztatotta az okokat és az indokokat egymástól, Davidson nem. Szerinte " … a cselekvés elsődleges indoka nem más, mint a cselekvés oka." [Donal] Anscombe-ék az egyik oldalon, Davidsonék a másikon. Egy cselekvéselmélet számára fontosabb az, amiben egyetértettek." … amikor indok által magyarázunk egy cselekvést, akkor valójában újraleírjuk azt; az újraleírás egy bizonyos mintába helyezi a cselekvést, és pontosan ezt nevezzük a cselekvés magyarázatának." [Donal]
A szándék modellje
A cselekvések magyarázatára hosszú időn keresztül alkalmazott vélekedés-vágy (Belief-Desire – BD) modellek kritikáját Michael Bratman végezte el [Micha] akinek fellépése óta már inkább vélekedés-vágy-szándék (BDI) modellről beszélnek. A dolgokat kissé leegyszerűsítve valóban mondhatjuk, hogy Bratman nem tett egyebet, mint a vélekedés és a vágy kategóriája mellé felvette harmadik mentális tényezőnek az intenció, (szándék, akarat) fogalmát. [♦] Kortársaihoz hasonlóan Bratman is úgy vélte, hogy az intenciónak két fajtáját különíthetjük el, a jövőre irányuló és a jelenre irányuló szándékot, és az utóbbi kifejezés jelentése megegyezik azzal, amikor azt mondjuk, hogy szándékosan cselekszünk valamit. Mielőtt tisztáznám, hogy mi a kétféle intenciófogalom jelentése, miben térnek el ezek egymástól, előtte szükség van néhány bratmani gondolat bemutatására. Felmerül rögtön a kérdés, hogy mi a vágy és a szándék fogalma közt a különbség. Bratman válasza erre az, hogy az elköteleződés (commitment) mozzanata jelenti a különbséget köztük. Az ugyanis nincs benne a vágyban, de benne van a szándékban. A szándék megváltoztatható, módosítható, támadható, visszavonható. A szándék olyan viselkedésbefolyásoló (conduct controlling) proattitűd (pro-attitide), aminek tehetetlensége (intertia) van és önmagában érveket szolgáltat a további mérlegelések számára. A szándék (és elköteleződés) szükséges a koordinációhoz, mégpedig a tervek megvalósításához szükséges cselekvések koordinációjához. A terv (plan) a szándékhoz hasonló fogalom, de a terv mindig a jövőre irányul. Bratman szerint az embernek mint tervező lénynek nagy szüksége van a részleges, hierarchikusan szervezett tervekre."Komoly pragramikus előnye lehet annak a stratégiának, amely a jövőre nézve részleges, hierachikusan strukturált terveket dolgoz ki. Egyfelől szükségünk van arra, hogy koordináljuk saját tevékenységünket akár magunkban, akár egymás közt vagyunk. Mindezt úgy kell megtennünk, hogy közben figyelembe kell vennünk a rendelkezésre álló információ feldolgozásával és mérlegelésével kapcsolatos korlátos kapacitásainkat. E korlátos kapacitás birtokában szükségünk van arra is, hogy előzetesen mérlegelhessük mindazon szempontokat, amelyek a későbbi viselkedéseinket formálják. Mindezek erős érvek a tervezés mellett. A világ azonban változik, és mi messze nem vagyunk abban a helyzetben, hogy jól előre is tudjuk jelezni ezt; a távoli jövőre vonatkozó, nagyon kidolgozott tervnek könnyen haszontalanná válnak, nem érdemlik meg a vesződést. Ilyenkor a részleges, hierarchikusan strukturált tervek jelenthetik a kompromisszumos megoldást." [Micha]
Két fontos követelményt lehet megfogalmazni a tervvel kapcsolatban. Egyfelől a tervnek az ember vélekedéseihez képest belsőleg konzisztensnek kell lennie (internally consistent), másfelől a tervnek cél-eszköz koherensnek kell lennie (means-end coherence). Ez a két minőség adja a tervek, szándékok, illetve a vágyak, értékelések közötti megkülönböztetés lehetőségét. A vágyakra nem érvényesítjük egyik kritériumot sem. A vágyra nem áll a belső konzisztencia követelménye. Két vagy több vágy lehet inkonzisztens bennem, de egy szándék vagy egy terv nem. Vágyhatok egyszerre meccsre menni és vacsorázni egyet este, de nem tervezhetem őket egyszerre végrehajtani. De a vággyal szemben nem várjuk el a cél-eszköz koherenciát sem, vagyis a vágyakhoz (mint lehetséges célokhoz) nem kell eszközöket rendelnünk, szemben a szándékokkal és tervekkel, amelyekhez igen. Azon a minősítésen, hogy a szándékaink alapján kidolgozott terveink részlegesek, azt kell értenünk, hogy nem minden részletükben kidolgozottak. Ez abban az értelemben hátrány, hogy ezeket a kidolgozatlanságokat ki kell a jövőben dolgozni a majdani körülményektől függően, de – és ez az igazán lényeges – pont e kidolgozatlanságok teszik lehetővé azt, hogy igazodhassunk a jövőben változó feltételekhez. A szándékok, tervek fontos szerepet visznek mindvégig a mérlegelés során, de fontos hangsúlyozni, hogy a szándékok nem szolgáltatnak érveket a cselekvés számára. A cselekvési indokokat a vágyainknak és vélekedéseinknek köszönhetjük. A súlyozást, az irányok és intenzitások kijelölését a hiteink által formált vágyaink, nem pedig a szándékaink végzik."A gyakorlati következtetésnek két szintje van: az előzetes szándékok és tervek felvetik a problémákat és egyfajta szűrőként működnek a potenciális megoldási lehetőségeken; a vágyak és hitek megfontolásokként szolgálnak az érvek súlyozásához a releváns és elfogadható kimenetek közötti mérlegelés során. Ez a kétszintű szerkezet fontos minősége annak a működésmódnak, ahogy a szándékok és tervek betöltik saját koordináció-támogató szerepüket, illetve segítenek nekünk elkerülni azt, hogy olyan időszeletelő ágenssé váljunk, aki állandóan a semmiből kezdi újra a számításait a mérlegelései során." [Micha]
Nagyon fontos eleme még az intenció jelenségének az a tény, hogy a jövőre irányuló vélekedéseink sok esetben lényegi módon a jelenbeli intencióinktól függenek. Az vélekedésem, hogy délben az egyetemen leszek, azon a tudásomon alapul, hogy oda szándékozom menni [Micha] Az intenció tehát elkötelezettséget jelent a versengő vágyak közepette, ami egyrészt azért fontos, mert – legalább időleges – állandóságot jelent, másrészt lehetséges további terveket ráépíteni. Szándékaink természetesen könnyen ellentmondásba keveredhetnek vélekedéseinkkel, de ebben a "konfliktusban" mindig sokkal inkább kritizálható a racionalitás szempontjából a szándékok és hitek közti inkonzisztencia, mint a köztük keletkező hiányosság, nem-teljesség. Bratman ezt nevezi az aszimmetria tézisének [Micha] A szándékok persze belsőek, így csak az introspekció révén adhatunk számot róla, míg a viselkedés külsőleg is megfigyelhető. A szándékok figyelembe vételével tudjuk csak megmagyarázni, hogy miért térnek el gyakran a cselekvések belső és külső értékelései. A belső értékelés figyelembe veszi (hiszen "ismeri") az elköteleződéseket és szándékokat, míg a külső megítélés eltekint ezektől. Szándékainkat, terveinket a mérlegeléseink során mindig újragondolhatjuk, és fontos kérdés, hogy mi a tervezés, a tervezés újragondolása és a racionalitás viszonya, de Bratman nézetét erről itt nem mutatom be. Elég csak annak rögzítése, hogy a szándékaink támadhatók, fölülbírálhatók, de mindenkor biztosítani tudnak egyfajta állandóságot, biztonságot nekünk."… korlátos adottságaink, illetve terveink azon szerepe miatt, hogy a jelen megfontolásainak érvényességét megbízható módon kiterjesztik a jövőbeni cselekvéseinkre nézve, számíthatunk arra, hogy a nem-újragondolásnak ez a hasznos jelensége élteti bennünk azt a hajlamot, hogy ne vizsgáljuk felül újra a már kész tervet kivéve persze, ha annak végrehajtásakor valamilyen problémával kerülünk szembe." [Micha]
A bratmani megközelítés nagy újdonsága a szándékok és tervek jelentőségének felismerése és ezek beemelése a cselekvés modelljébe. Ehhez képest másodlagosak azok a kritikák, amelyek a Bratman utáni korszak mérnöki megközelítéseiben merültek fel. Stuart J. Russel és Devika Subramanian például a racionalitás – túlzottan erős – elvárását kritizálták a bratmani elképzelésben, és a "teljes racionalitás" helyett a jóval "gyengébb" aszimptotikus korlátozott optimalitás (APO – Asymptotic Bounded Optimality) fogalmának alkalmazását javasolták helyette [Stuar] E kritikát lehet megalapozottnak tartani, de a cselekvéselméleti modell építése szempontjából ezt nem tartom kardinális kérdésnek. Másfajta racionalitáselképzelések mentén is meg lehet, sőt, szerintem meg kell tartani az intenció (szándék, terv) fogalmának Bratman által javasolt kiemelt szerepét a BDI-modellen belül. Philip R. Cohen és Hector J. Levesque logikai formalizmust dolgozott ki Bratman intencióelméletére, ami azóta is gyakran hivatkozott forrás a mérnökök körében [Cohen] Már eleve beszédes a cikk címe: "A szándék elkötelezett választás" ("Intention is choice with commitment"), ami mutatja, hogy a szerzők azt a bratmani tételt tették a kidolgozott logikájuk központjába, amely szerint a szándék az a választás, amely mellett az egyén elköteleződik. Mivel szándék, az intenció, az akarat terminusait mind ugyanezen értelmezés mentén javaslom használni, ezért ezeket a terminusokat mind ehhez a fogalomhoz kapcsolom a cselekvéselmélet modelljében. Cohenék felsorolták a szándék hát legfontosabb jellemzőjét, amit érdemes itt felidéznünk.- a szándék szokásos esetben valamilyen feladatot jelent az ágens számára, aminek megoldásához valamilyen – cselekvési – utat kell találnia (ha egy másik városban kell lennem másnap, akkor meg kell terveznem, hogy jutok el oda, kocsival, vonattal, biciklivel, valamit mindenképp tennem kell);
- a szándék valamiféle megvalósíthatósági keretet jelöl ki a későbbi szándékok számára (a vágyak lehetnek inkonzisztensek, a szándékok nem: ha kocsival akarok elmenni a szomszéd városba, akkor nem akarhatok biciklivel is menni);
- az ágens "nyomon követi" szándékai megvalósítása érdekében végzett lépéseit, és ha kell, alakít az eredeti elképzelésein (ha elindulok biciklivel, de az első saroknál kidurran a kerékgumi, visszafordulok, és kocsira váltok);
- az ágensnek hinnie kell abban, hogy a kitűzött célja megvalósítható, nem irányulhat a szándéka tudottan lehetetlen dolgok elérésére (ha fél óra múlva a másik városban kell lennem, amit biciklivel lehetetlen ennyi idő alatt elérni, akkor a kocsi használatára irányulhat a szándékom, a bicikliére nem);
- az ágens nem hiheti azt, hogy nem fogja előidézni a cél megvalósulását (nem hihetem azt, hogy vadászrepülővel fogok átmenni a szomszéd városba, amikor tudom, hogy nincs leszállópálya se itt, se ott, nincs repülőgép, nem tudok repülőt vezetni);
- az ágens hisz abban, hogy bizonyos feltételek mentén megvalósíthatja a célját (hinnem kell abban, hogy ha van benzin a kocsimban, nem durran ki menet közben a kereke, tudok vezetni, van jogosítványom, akkor odajuthatok a másik városba);
- az ágensnek nem kell akarnia a szándéka minden várható következményét is egyben (ha tudom, hogy kocsi használatának lesz benzinköltsége, ami a bicikli esetén elmaradna, de mégis kocsival akarok utazni, attól még nem akarom direkt kiadni a benzinre a pénzt).
$\concept{INTEND}_1(x,a) \defi$ $\concept{PERSISTENT-GOAL}(x,(\concept{DONE}(x,\concept{BELIEF}(x,\concept{HAPPENS}(a)))?;a))$
szándékozni (hun) – intend (eng)
A fogalmak paraméterei között az x változó az ágenst, az a a tetszőleges cselekvést jelöli. A formulát pedig úgy értelmezhetjük, hogy az ágensnek szándékához szükség van elköteleződésre, amit részben a perzisztens cél fogalmával fejezhetünk ki. Ez azonban még kevés lenne a szándék megragadáshoz, mert ez elvileg teljesülhet véletlenek sorozatán keresztül. Emellett szükség van arra is, hogy az ágens célra irányulását is leírjuk valahogy. Ezt fejezi ki a formula három egymásba ágyazott eleme: az ágensnek előzetesen hinnie kell (belief$(x,a^{'})$) a célul kitűzött cselekvés megvalósulásában (happens$(a)$), aminek aztán ténylegesen meg is kell valósulnia (done$(x,a^{"})$). A formula végén található műveleti jelek a dinamikus logika operátorai. A formula tehát azt a bratmani tézist fejezi ki, hogy a szándék (akarat) a választott vágy melletti elköteleződést jelenti. Talán van, akinek meglepő, biztos van, akinek nem, de tény, hogy az akaratnak ezt a felfogását már a korábbi nagy elődök közül is többen magukénak vallották. Nem tartom valószínűnek, hogy Bratman, Cohen vagy Levesque sokat olvasta volna Thomas Hobbes, Arthur Schoppenhauer vagy Edmund Husserl műveit, mert ha így tettek volna, akkor rájöhettek volna, hogy előttük már jóval korábban is megfogalmazták az akarat elköteleződéssel kapcsolatos szoros viszonyát. Hobbes esetében talán még nem látszik annyira ez a fogalmi kapcsolat, amikor a vágy és akarat viszonyáról ír, de Schoppenhauer és Husserl esetében nyilvánvaló az összefüggés tételezése. Hobbes ezt írta:"A megfontolásban a cselekvésre vagy annak elmulasztására közvetlenül rátapadó legutolsó étvágy vagy ellenszenv, ez az, amit akaratnak hívunk; az akarás tette (nem a képessége)." [hobbe]
Furcsa, ahogy Hobbes étvágyról ír, de azért az nyilvánvaló, hogy a vágyra gondol, amit viszont nem nehéz összekapcsolni a preferencia vagy a választás fogalmaival, és 'legutolsó' vágy (vagy ellenszenv) minősége egyértelműen az elköteleződés mozzanatára utal. Schoppenhauer az akarat szabadságáról szóló híres könyvében deklarálta a következőket."Tehetsz, amit akarsz: de élted minden adott pillanatában csak egy határozott dolgot és szükségképen csakis ezt az egyet akarhatod, semmi mást. [schop]
"Az öntudatnak egyetlen tárgy az akarati tény és annak feltétlen uralma a test tagjai felett, ezt értjük voltaképpen azon, hogy tehetek, » amit akarok«. Csupán ennek az uralomnak a gyakorlása, vagyis a tett, bélyegzi (az akaratot), még az öntudat számára is, akarati ténynek. Mert amíg keletkezőben van, addig kívánság a neve, ha kész, akkor elhatározás. De hogy valóban elhatározás, azt még az öntudatnak is csak a tett bizonyítja be, mert mindaddig változékony. …
Kívánni lehet ellentétest, de akarni csak az egyiket közülük: még pedig hogy melyiket, azt az öntudatnak is csak a tett teszi nyilvánvalóvá."
[schop]
"… az akarati tételezés a maga sajátos tartalmával (az akart céllal), minden további nélkül létrehozza azt a maradandó célra maradandóan irányuló akarást, amely a pillanatnyi, tovaáramló aktuson túlmutat. … Az » Akarom« tehát sokkal inkább azt jelenti: kitűzöm vagy már korábban kitűztem magamnak a célt, és ettől kezdve folyamatosan – ameddig valami egyéb nem történik – én vagyok az, akinek ez a szándéka, aki ezzel az » akarattal« rendelkezik." [Edmun]
Bármennyire is másra fókuszál Husserl a cikkében, az idézett sorok magukban rejtik azt a mozzanatot, amiről eddig szó esett: az intencionális élmények folyamatosan változó áramában a célra mint saját tartalmára irányuló akaratot az állandósággal, a maradandósággal ragadhatjuk meg. A cikk egy későbbi pontján az akaratról mint "megmaradó elhatározásról" ír Husserl [Edmun] és ezzel a maradandó célra irányulás minőségével voltaképp az elköteleződés minőségét fejezi ki. Vagy mondhatnánk akár fodítva is: az elköteleződést magát definiálhatjuk a célok, vágyak megmaradóságának tulajdonságával. Ennek meglehetne az az előnye, hogy az itt használt 'elköteleződés' fogalmat kicsit távolíthatnánk a beszédaktusok, valamint a normativitás világában fontos szerepet betöltő 'elköteleződés'-értelmezésektől. Máshol már utaltam rá, amit most újra megerősítek, hogy bármennyire is fontos kérdésnek tartom akaratszabadság filozófiailag releváns problémáját, én itt nem tudom, nem is akarom tárgyalni. Mindaddig, amíg az első- és másodrendű akaratokról, az akaratkonfliktusról mint egy személyen belül jelentkező problémáról beszélünk, addig a filozófiát érzem illetékesnek. Abban a pillanatban azonban megváltozik minden, ha két vagy több személy egymással konfliktusba kerülő akaratáról és az akaratok megtörésére szolgáló kényszerek különböző formáiról van szó, mert ez a jelenség már nagyon is a társadalmi cselekvések szociológiai tárgykörébe tartozónak vélem. Ezt azonban nem itt, hanem a hatalom és az uralom jelenségénél kell tárgyalni. Érdemes lenne az akaratszabadság kérdését a legújabb kognitív tudományi, neurológiai kísérletek fényében is körbe járni, de ezek tárgyalását – bár nagyon fontosnak és relevánsnak tartom őket – megintcsak mellőzhetőnek vélem. Benjamin Libet készenléti potenciállal kapcsolatos kísérlete óta ismert az a nézet, mely szerint valójában nincs igazán szabad akaratunk, mert már az akaratunk tudatosulása előtt dönt az agy, ami a készenléti potenciál állapotában kimutatható [Danie] Vannak, akik támogatják, vannak, akik vitatják Libet eredményeit. [♦]A vélekedések és vágyak dinamikája
Cristiano Castelfranchi és Fabio Paglieri olyan logikát dolgoztak ki, aminek középpontjában a vélekedések célkövetés dinamikájában betöltött szerepe áll. [Crist] A célok és szándékok kitűzésének, változtatásának, megvalósításának folyamatát Castelfranchi és Paglieri azt feltételezve vélik megragadhatónak, hogy a célok követését, a szándékok felülvizsgálatát legnagyobb részben a hiteink befolyásolják, és ezt az összefüggésrendszert érdemes kibontani, részleteiben megvizsgálni, leírni. Ha így teszünk, szakaszokra bonthatjuk ezt a folyamatot a célok aktiválásától kezdve a szándékok képzésén át, a célok és szándékok menet közbeni revízióján keresztül a célok, a cselekvések végrehajtásáig. Eközben különböző cél- és vélekedéstípusokat különíthetünk el egymástól, melyeket tipikus módon hozzárendelhetünk a folyamat egyes szakaszaihoz. Egy ilyen felbontású leírás sokkal pontosabb magyarázatot adhat a célkövető, mérlegelő cselekvésre. A vélekedéseink és a céljaink egyaránt mentális reprenzentációknak tekinthetők, amelyek funkcióikban különböznek egymástól, nem pedig formájukban, tartalmukban vagy más belső jellemzőikben. Castelfranchiék itt használt cél fogalma közel van a mesterséges intelligencia világának vágy és szándék, a kognitív pszichológia motiváció, kívánság és cél vagy a társadalomtudományok preferencia fogalmaihoz."… a cél úgy definiálható, mint egy, a jövőben feltételezett világállapotra vonatkozó belső reprezentáció, amelynek rendelkezik egyfelől azzal a potenciálal, másfelől azzal a funkcióval, hogy egy ágens viselkedését a cél megvalósításának irányába kényszerítse/vezesse. A célok meghatározó funkciója teleológiai értelemben formálni, irányítani a rendszer tényleges viselkedését" [Crist]
A célok olyan, a jövőre nézve kialakított állapotok, amelyek ellentétesek a világnak azon jelen állapotaival, amelyek aktuálisan léteznek vagy inkább, amelyekről az érintett ágensek feltételezik (létezni vélik). A célkövető folyamat értelmezéséhez szükség van a vélekedések, hitek tipizálására. Kétféle hitet különíthetünk el a célvonatkozású vélekedéseken (goal-related belief) belül: céltámogató vélekedéseket, illetve vélekedéstámogató vélekedéseket. A céltámogató vélekedéseknek (goal-supporting belief) nélkülözhetetlen szerepe van a célok fenntartásában. A vélekedéseinknek ugyanis speciális struktúrába kell összeállniuk ahhoz, hogy fenntartsák, igazolják magukat a célokat. Az ilyen vélekedések hiányában az adott cél elválna az aktuális állapottól, megváltozna mind a természete, mind a funkcionális tulajdonságai. Mivel Castelfranchiék a vélekedéstámogató vélekedések (belief-supporting beliefs) fogalmát akarják elemezni a cikkükben, ezért ezt a fogalmat alaposabban kibontják. Az alábbi típusokat sorolják be alá.- motivációs hitek (motivating beliefs)
ezek a hitek késztetnek cselekvésre minket, bár ezek mellett léteznek nem-doxasztikus befolyások is, például az belső készenléti szintünk állapota vagy az érzelmi reakciók (physical arousal, emotional triggering)- - kiváltó hitek (triggering beliefs)
- - feltétel hitek (conditional beliefs)
- előszűrő/előértékelési hitek (assessment beliefs)
ezek a hitek előszűrik a vélekedéseket, és ezzel kialakítják a követhető célok körét- - önmegvalósulási hitek (self-realization beliefs)
- - megvalósultsági hitek (satisfaction beliefs)
- - lehetetlenségi hitek (impossibility beliefs)
- költségbecslő hitek (cost beliefs)
ezek a hitek a folyamat egyes összetevőihez rendelhető költségek (ráfordítások, nehézségek) nagyságára, típusára vonatkoznak - inkompatibilitási hitek (incompatibility beliefs)
ezek a hitek segítenek abban, hogy ki tudjuk szórni a mérlegelésbe vont célok, eszközök közül azokat, amelyek valamilyen szempontból diszkrepanciát, inkompatibilitást okoz(hat)nak- - végcél inkompatibilitási vélekedések (terminal incompatibility beliefs)
- - instrumentális inkompatibilitási hitek (instrumental incompatibility beliefs)
- - feleslegességi imkompatibilitási hitek (superfluity)
- preferencia hitek (preference beliefs)
ezek a hitek "tartalmazzák" a preferenciáinkat, azok – főleg időbeli – intenzitásait- - érték hitek (value beliefs)
- - sürgősségi hitek (urgency beliefs)
- előfeltétel hitek (precondition beliefs)
ezek a hitek azokra az előfeltételekre vonatkoznak, amelyek a folyamat sikeréhez elengedhetetlenek- - inkompetencia hitek (incompetence beliefs)
- - feltételhiány hitek (lack of conditions beliefs)
- cél-eszköz hitek (means-end beliefs)
ezek a hitek rendelik össze a potenciális célokat a megvalósításukhoz szükséges eszközökkel
| aktiválás | $ \rightarrowtail$ | értékelés | $ \rightarrowtail$ | mérlegelés | $ \rightarrowtail$ | ellenőrzés | $ \rightarrowtail$ | cselekvés | ||||||
| (activation) | (evaluation) | (deliberation) | (checking) | (action) | ||||||||||
- aktív célok (active goals) = vágyak (desires)
- követhető célok (pursuable goals)
- válaszott célok (chosen goals)
- végleges/végehajtandó célok (executive goals)
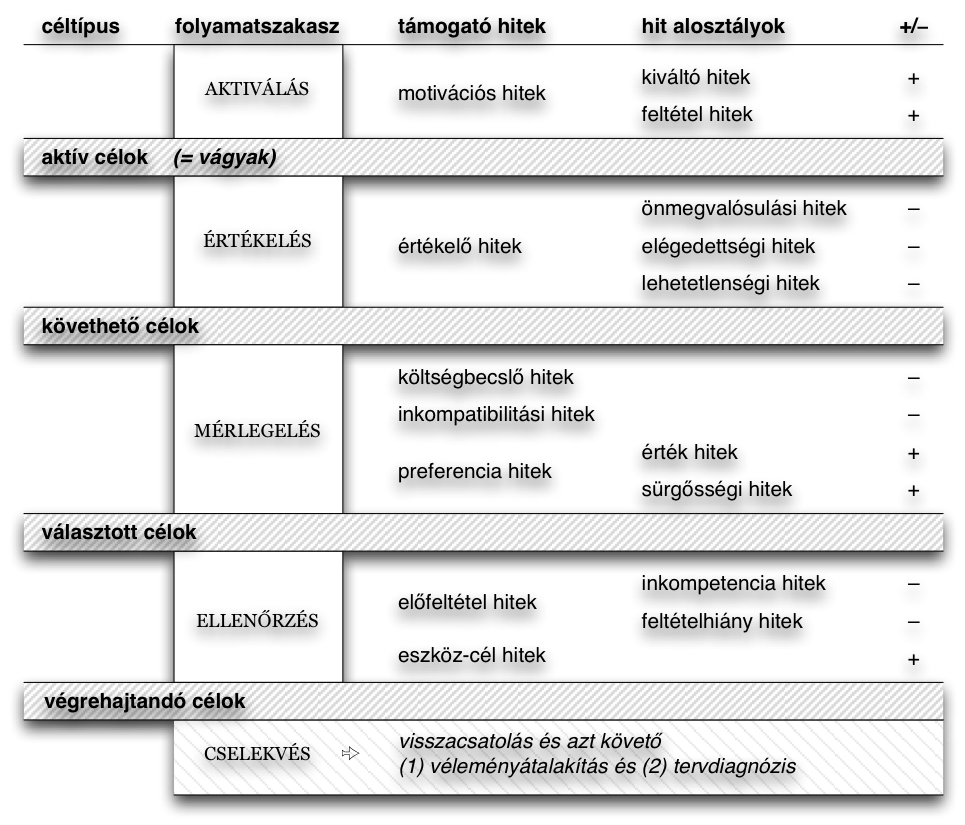
Ahogy a folyamatban haladunk előre, az egyes folyamatszakaszokban releváns vélekedéseink formálják a céljainkat, míg a végén ki nem alakul a végrehajtandó cél. Egy ilyen folyamat természetesen nem feltétlenül fut végig, pontosabban nem feltétlen ad végeredményt, vagyis nem biztos, hogy mindig találunk végrehajtható célokat. Az ábra jobb oldalán látható annak jelzése, hogy az egyes hitek hogyan járulnak hozzá a folyamat pozitív beteljesedéséhez. A pozitív minősítési hitek "támogatják" a célkiválasztási folyamatot, a negatív előjelű hitek a célok megvalósíthatóságának "útjában állnak". Ami az ábrán nem igazán látszik, de a folyamathoz hozzátartozik, az a visszacsatolás és a cél- vagy tervfelülvizsgálat szakasza a cselekvési folamat egészén belül. Ezt úgy kell elképzelnünk, hogy a célkiválasztás után elindított cselekvési folyamat során a visszacsatolás eredményeként esetleg szükségessé váló újratervezés végigmehet az itt leírt célkiválasztási folyamat majdnem minden lépcsőfokán. A bemutatott folyamatábra a mérlegelő beállítódás, a racionális célkiválasztás folyamatát írja le. Nem foglalkozik azzal, hogy a választást magát hogy lehet értelmezni. A következő fejezetben áttekintem, hogy – a közgazdaság-tudományon belül – milyen értelmezéseket adtak a választás fogalmának, illetve a vele kapcsolatba hozható más, rokon kategóriáknak.
Választás
Ahhoz, hogy a választás fogalmát definiálni tudjuk, szükségünk van pár kisegítő fogalomra. A választás alternatívák összehasonlítását, majd az összehasonlítási szempont szerinti legjobb elem(ek) kijelölését jelenti. A választás fogalmának meghatározása előtt így meg kell tudnunk mondani, mit jelent a legjobb elem fogalma. Ha adva van egy halmazunk, amin értelmezve van egy bináris reláció, akkor mindig megvizsgálhatjuk, hogy az adott reláció szerinti rendezés eredményeként lesz(nek)-e legnagyobb elem(ek). Ha igen, akkor ezek segíthetnek minket a választás fogalmának meghatározásához. Látni kell azonban, hogy ezek a tulajdonságok elsődlegesen nem magára a relációra, hanem a tartóhalmaz egy vagy több elemére vonatkoznak, de a legjobb, legnagyobb elem fogalma megkívánja a rendezési reláció létét a definícióban, vagyis ezek az extremitást kifejező fogalmak a halmaz és reláció fogalmára egyaránt támaszkodnak [Kotar] A következőképpen.$\concept{GREATEST}\equiv G(S,\rel{R}) \defi (S\subset\mathbb{X} \land \rel{R}\subset\mathbb{X}\times\mathbb{X})\to \{m\in S | \forall n\in S: (m,n)\in \rel{R}\}$
($\rel{R}$-)legnagyobb (elem) (hun) – ($\rel{R}$-)greatest (element) (eng) – legjobb (elem) (hun) – best (element) (eng) – {G}-optimális (elem) (hun) – {G}-optimal (element) (eng) – (felülről) domináns elem (hun)
$\concept{MAXIMAL}\equiv M(S,\rel{R})\defi ()\to \{m\in S | \forall n\in S: (n,m)\notin \rel{P(R)}\}$
($\rel{R}$-)maximális (elem) (hun) – ($\rel{R}$-)maximal (element) (eng) – {M}-optimális (elem) (hun) – {M}-optimal (element) (eng) – (felülről) nem domináns elem (hun)
Mind a legnagyobb, mind a maximális elem valamiféle extremitást jelent. Ha meg akarjuk érteni azt, hogy miben különböznek egymástól, akkor ebben leginkább az segíthet, ha felidézzük a preferenciastruktúrára vonatkozó tételeket, azok közül is leginkább a szigorú preferenciarendezés, valamint annak konverze, az indifferencia és az összehasonlíthatatlansági reláció mint négyes partíció létezésére vonatkozó tételt (☜) Utóbbi szerint az említett négy reláció egymást kölcsönösen kizárja, és együttesen pedig kiteszik az univerzális relációt. Ebből viszont az következik, hogy amíg a legnagyobb elemek halmazába azok az elemek tartoznak, amelyek kielégítik a szigorú preferenciarendezés, illetve az indifferencia reláció feltételeit, addig a maximális elemek halmaza azokból az elemekből áll, amelyek nem felelnek meg a konverz szigorú preferenciarendezésnek, vagyis amelyek kielégítik vagy a szigorú preferenciarendezés vagy az indifferencia vagy az összehasonlíthatósági reláció feltételeit. Ebből perdig nyilvánvalóan az következik, hogy a legnagyobb, illetve a maximális eleme halmazok között az összehasonlíthatatlansági reláció jelenti a különbséget. Ezt úgy is megfogalmazhatjuk, hogy a legnagyobb eleme halmazban azok az elemek vannak, amelyek minden más elemnél "nagyobbak" és egymás között indifferencia reláció áll fent, a maximális eleme halmaz pedig azokat az elemeket tartalmazza, amelyek elemei között vagy az indifferencia vagy az összehasonlíthatatlansági reláció érvényesül. A legnagyobb elemek mind indifferensek egymáshoz képest, a maximális elemek vagy indifferensek vagy összehasonlíthatatlanok. Az igazi különbség az összehasonlíthatatlansági relációban van. A két extremitás között két további fontos összefüggést is megállapíthatunk [Walte] Egyfelől igaz az, hogy $G(S,\rel{R})\subset M(S,\rel{R})$, vagyis a legnagyobb elemek halmaza mindig része a maximális elemek halmazának, másfelől bizonyítható az a tétel is, hogy ha egy reláció teljes és reflexív, akkor a maximális és legnagyobb elemek halmaza megegyezik. Az extremitások, azaz legnagyobb (legjobb) és maximális elem fogalmaira támaszkodva már meg lehet határozni a választási függvény fogalmát, de előtte még tisztázni kell pár dolgot. Első lépésként be kell vezetni a $(\mathbb{X},\mathscr{S})$ választási tér fogalmát, ahol $S \subset \mathbb{X} (S\in\mathscr{S})$ az alternatívák teljes $\mathbb{X}$ halmazán képzett részhalmazokat, vagyis az ágens számára a választás során elérhető állapotok halmazait jelentik, $\mathscr{S}$ pedig az S részhalmazok hatványhalmazát. A választási halmaz a választási tér valamelyik konkrét S halmazának egy nem-üres részhalmaza, és a választási függvény a választási tér választási halmazra való leképezését végzi el.$\concept{CHOICE\_FUNCTION}\defi \forall S\in\mathscr{S}(C: \mathscr{S} \mapsto C(S) \;|\; C(S)\ne\emptyset)$
választási függvény (hun) – choice function (eng) – döntési függvény (hun) – decision function (eng)
A választási függvény alapján előállt választási halmazok elemei még nincsenek rendezve. Vannak a kiválaszottak, azok az elemek, amelyek $C(S)$-ekbe tartoznak, és vannak a választhatók, azok az elemek, amelyek S-ekbe tartoznak.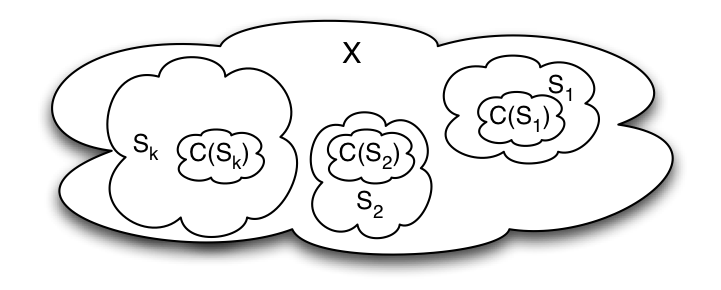
Itt még nem feltétel a választási függvény egyeleműsége, lehet benne több kiválaszott elem is. Ha ez fordul elő, akkor döntetlentörő szabályok szerint lehet eldönteni a végleges (egyetlen) választást, de ez nem jelent igazi problémát, nem is nagyon fogom elemezni. Érdemes viszont pár példát bemutatni a választási függvényre, mégpedig olyanokat, amelyek majd szembeállíthatók a később bevezetendő racionális választási függvény fogalmával. A lottósorsolás esetében az alternatívák halmazát a leadott szelvények jelentik, és a választás a véletlen alapján történik meg. A résztvevők megtippelik a számokat, és a gép véletlenszerűen választ a számok közül, de ezzel voltaképp a leadott szelvények (és áttételesen az azokat birtokló személyek) közül választ ki egyet vagy többet. Ez a példa mutatja azt is, hogy a választási halmaz fogalma még megengedi, hogy a procedúra több kimenetet adjon. A döntetlentörő szabály itt annyi, hogy a nyereményt annyi részre kell osztani, ahányan bekerültek a választási halmazba. A lottóhúzáshoz képest csak egy ponton van különbség a tombolajáték esetében, amikor a leadott szelvények közül – megintcsak véletlenszerűen – egyetlen győztest húznak ki a "jelöltek" közül. A véletlen választás elve mellett létezik más nem-racionális módszer is. Például az általános iskolai osztályokban a hetes szerepébe a névsor szerinti kerülnek be a tanulók. Ilyenkor is választásról beszélünk, hiszen egy alternatívahalmazból egy (vagy több) elemet kiválasztunk. Meg lehetne szavaztatni mindenkit arról, hogy ki legyen a hetes, lehetne pénzfeldobással dönteni, és lehetne a nevek kezdőbetűi alapján. Ezt a mechanikus elvet egyébként alkalmazzák, alkalmazták a politika világában is. Amikor még létezett Jugoszlávia, akkor a tagországok vezetőiből álló államelnökség tagjai közti úgy döntötték el, hogy ki legyen az államelnök egy adott időszakra, hogy az államok neve szerinti sorrendben váltották egymást a tagországok vezetői. De a görög városállamokban is előfordult, hogy bizonyos tisztségek betöltésére a névsor szerint jelölték ki a polgárokat egymás után. Ezek a példák szépen mutatják azt is egyben, hogy a választási függvény létezése önmagában még nem "garantálja" annak racionális jellegét. Pedig a racionalitás feltételének érvényesülését jó lenne elvárni. Ezt a minőséget valamilyen gyenge rendezési preferenciarendezési reláció, illetve az ennek alapján képzett legnagyobb elem halmaz választási függvényhez rendelésével biztosíthatjuk.
$\concept{G-RATIONAL\_CHOICE\_FUNCTION}\defi \exists \rel{R}\subset\mathbb{X}\times\mathbb{X} \;\forall S\in \mathscr{S}(C(S)=G(S,\rel{R}))$
(G-)racionális választási függvény (hun) – (G-)rational choice function (eng)
Akkor racionális egy választási függvény, ha az általa kiválasztott választási halmaz megegyezik egy adott gyenge preferenciarendezés szerinti legnagyobb elemek halmazával. A racionalizálást tehát a preferenciarendezés "végzi el" (mondhatjuk is azt, hogy az adott preferenciareláció a választás/döntés racionalizálása). Ez azért is tűnik szerencsés megoldásnak, mert így jobban kezelni tudjuk azt a vitatott kérdést, hogy ti. milyen kritériumai is vannak a racionális választásnak. Ha megengedjük, hogy a preferenciareláció többféle lehessen, akkor nem kell kizárólagos módon állást foglalnunk ebben a kérdésben, és a fenti meghatározáshoz képest elfogadhatunk másfajta racionalitásértelmezéseket is. Például ha a másik extremitásfogalmat, a maximális elem kategóriáját alkalmazzuk itt, akkor máris más racionális választási függvényhez jutunk.$\concept{M-RATIONAL\_CHOICE\_FUNCTION}\defi \exists \rel{R}\subset\mathbb{X}\times\mathbb{X} \;\forall S\in \mathscr{S}(C(S)=M(S,\rel{R}))$
(M-)racionális választási függvény (hun) – (M-)rational choice function (eng)
Van tehát egy választási függvényünk, van egy hozzárendelhető preferenciarelációnk, amire vonatkozóan különböző minőségű és erősségű tulajdonságokat tételezhetünk abban a reményben, hogy ezáltal jellemezni tudjuk a választói döntéseket, beállítódásokat."Akkor tekintünk egy aggregált gazdasági szereplőt – tehát a döntési függvényét – racionálisnak, ha bevezethető olyan reláció az alternatívák halmazán, amely szerinti optimalizáló választás ugyanazt eredményezi, mint a döntési függvény szerinti választás. Világos, hogy ebben a keretben annyiféle racionlitás vethető fel, amennyi tulajdonsága lehet a racionalitást biztosító relációnak, így a tranzitivitás ennek csak egy fontos speciális esete." [Magya]
Ez a hozzáállás azt is lehetővé teszi, hogy a preferenciarelációra vonatkozó feltételek mentén különböző erősségű racionalitáskritériumokat állítsunk fel a választási függvényre vonatkozóan. Hogy ezt megtehessük, szükségünk van még egy fontos fogalomra, amivel kapcsolatot teremthetünk a választás és racionalitáskritériumot "szállító" reláció között. Ehhez fel kell idéznünk a közgazdaságtan egyik központi kategóriáját, a kereslet fogalmát. A közgazdászok ezt a fogalmat nagyon mélyen beágyazták a mikroökonómia szövetébe, ami – sok minden mellett – azért is különösen fontos volt a közgazdaságtan számára, mert "külsőleg" lehetett mérni – szemben a preferencia (vagy a hasznosság) fogalmával, amit meg nem. A kereslet változását a jószágok fogyasztásán keresztül "objektíven" követhetjük, mérhetjük, a jószágokra vonatkozó "belső" hasznosság szubjektíven érezhető, a megfigyelőnek nincs direkt hozzáférése. A közgazdászok körében sokáig vitatott volt, hogy a hasznosságot (preferenciát) és keresletet hogyan lehet összekapcsolni egymással. Az áttörést a – Paul A. Samuelson és Hendrik Hoathakker nevéhez köthető – kinyilvánított preferencia fogalmának megjelenése hozta el [Kovac] Samuelsonék újítása az volt, hogy a – keresletet generáló – fogyasztók vásárlásait, választásait értelmezhetjük úgy, mint saját belső preferenciáik kinyilvánításait, és az egyének választásainak teljes halmaza voltaképp az egyének preferenciáit adja meg. Erre már fel lehet írni egy összefüggést, és akkor a preferencia fogalma "kezelhetővé" válik. [♦] A választás és a kinyilvánított preferencia közti kapcsolat persze többféleképpen is értelmezhető, adhatunk egy erős és egy gyenge meghatározást, az alábbiak szerint.$\concept{WEAKLY\_REVELALED\_PREFERENCE}\equiv\rel{R}_c\defi \bigcup \limits_{S\in\mathscr{S}} [C(S) \times S] $
gyengén kinyilvánított preferencia(reláció) (hun) – weakly revealed preference (relation)(eng) – Richter-reláció (hun) – Richter-relation (eng)
$\concept{STRONGLY\_REVELALED\_PREFERENCE}\equiv\rel{R}_c^{\ast}\defi \bigcup \limits_{S\in\mathscr{S}} [C(S) \times \{S \setminus C(S) \}] $
erősen kinyilvánított preferencia(reláció) (hun) – strongly revealed preference relation (eng) – Samuelson-reláció (hun) – Samuelson-relation (eng)
Mindkét relációnak ugyanaz a lényege. Létezik az alternatívák teljes készletének egy olyan halmaza, amelynek m is, n is eleme, és ezek közül az egyén az előbbit preferálja az utóbbival szemben, vagy másként az egyén mindkét elemet választhatta volna, de ténylegesen az m-t választotta. A kétféle értelmezés csak abban tér el egymástól, hogy az egyikben megszorítás van a preferenciareláció második argumentumára vonatkozóan (a formulában $S \setminus C(S)$ szerepel a S helyett), míg a másikban nincs. Ezt úgy interpretálhatjuk, hogy az egyén n-t választhatta volna, de nemcsak, hogy nem választotta, de aktuálisan még vissza is utasította (ezt fejezhetjük ki azzal a szűkítéssel, hogy n mindig csak az S-nek azon részhalmazában szerepelhet, amely az S alaphalmaz és a $C(S)$ választási részhalmaz különbsége). A továbbiakban a választási függvénnyel, a kinyilvánított preferenciarelációval kapcsolatos racionalitásértelmezéseket Kotaro Suzumura megközelítését elfogadva mutatom be, aki könyvében precízen és kimerítően tárgyalja ezt a témakört [Kotar] Történelmileg Samuelsonék axiómái voltak az elsők, amelyek kényszereket fogalmaztak meg a kinyilvánított preferencia fogalmára vonatkozóan. Samuelson feltételét el is nevezték gyenge axiómának, míg Houthakkerét erősnek. Ezek mellé Suzumura definiált egy harmadik kritériumot is, amit Houthakkerről nevezett el, és a három fogalmat az alábbi módon definiálta.$\concept{(WARP)}\defi \forall m\forall n \in \mathbb{X}(\rel{R}_c^{\ast}(m,n)\to\lnot \rel{R}_c(m,n))$
kinyilvánított preferencia gyenge axiómája (hun) – Weak Axiom of Revealed Preference (eng) – Weak Axiom of Consumer Behaviour (eng)
$\concept{(SARP)}\defi \forall m\forall n \in \mathbb{X}([\rel{R}_c^{\ast}]^{+}(m,n)\to\lnot \rel{R}_c(m,n))$
kinyilvánított preferencia erős axiómája (hun) – Strong Axiom of Revealed Preference (eng) – Strong Axiom of Consumer Behaviour (eng)
$\concept{(HARP)}\defi \forall m\forall n \in \mathbb{X}([\rel{R}_c]^{+}(m,n)\to\lnot \rel{R}_c^{\ast}(m,n))$
kinyilvánított preferencia Houthakker axiómája (hun) – Houthakker's Axiom of Revelaed Preference (eng)
Mindhárom tulajdonság esetén szerepel a gyenge és erős értelemben kinyilvánított preferencia a definícióban, és kétszer alkalmazni kell az adott relációra az $\rel{R}^{+}$ tranzitív lezárás műveletét is (☜) Amartya K. Sen a 1970-es években írt cikkeiben több racionalitáskritériumot is megfogalmazott, és ezeket $\alpha$-, $\beta$, $\gamma$-tulajdonságoknak nevezte el. Maga Sen is megjegyezte, hogy az $\alpha$-tulajdonság megegyezik Herman Chernoff által definiált tulajdonsággal, amit a tétel megjelenése óta Chernoff-axiómának neveznek [Chern] Elsőre bemutatom, ahogy Sen megadta az $\alpha$-tulajdonság definícióját, majd másodjára melléteszem azt a formulát, ahogy Suzumura fejezte ki Chernoff axiómáját.$\concept{(SEN-}\alpha\concept{)}\defi \forall m((m\in S_1\land \;S_1\subset S_2) \to (m\in{C(S_2)} \to m\in{C(S_1)}))$
Sen $\alpha$-tulajdonsága (hun) – Sen's $\alpha$-property (eng) – irreleváns alternatívák függetlensége (hun) – independence of irrelevant alternatives (eng) – (basic) contraction consistency (eng)
$\concept{(CA)}\defi \forall S_1\forall S_2\in \mathbb{S}(\;S_1\subset S_2 \to (S_1\cap C(S_2)=\emptyset \lor S_1\cap C(S_2)\subset C(S_1)))$
Chernoff axiómája (hun) – Chernoff's axiom (eng) – örökítő (hun) – öröklődő (hun) – megőrző (hun) – preserving (eng)
Sen azt javasolta, értelmezzük úgy ezt a tulajdonságot, hogy ha a világbajnok egy pakisztáni, akkor ennek a világbajnoknak Pakisztán bajnokának is kell lennie [Amart] Ez a kritérium az örökítésről, örökletességről szól. Ha egy nagyobb halmazból kiválasztunk valamit "győztesnek", akkor annak bármely olyan részhalmazából is ki kell választanunk ugyanazt a győztes, amely részhalmazok tartalmazzák azt a legjobb elemet. Sen megjegyezte még, hogy erre a feltételre használják az irreleváns alternatívák függetlensége kifejezést is, de fontos tudni, hogy ilyenkor ezt más értelemben teszik, mint ahogy az a társadalmi választások elméletében szokás (☜) Itt az egyén racionalitásának jellemzésére, ott a kollektív preferencia kialakítását végző eljárás egyik kritériumaként használják ezt a terminust. Kenneth J. Arrow egy 1959-es cikkében definiált egy tulajdonságot [Kenne] ami egyetlen apró mozzanatban tért csak el a Chernoff axiómától. Arrow tulajdonságát később Suzumura elnevezte Arrow-axiómának, és a következő formában mutatta be.$\concept{(AA)}\defi\forall S_1\forall S_2 \in \mathbb{S}(S_1 \subset S_2 \to(S_1\cap C(S_2)=\emptyset \lor S_1\cap C(S_2)=C(S_1)))$
(választás konzisztenciájának) Arrow axiómája (hun) – Arrow's axiom (of choice consistency) (eng) – Arrow's independence condition (eng) – erősen örökítő (hun) – erősen megőrző (hun) – strongly preserving (eng)
Az a pici kis eltérés, ami megkülönbözteti a Chernoff- és az Arrow-axiómákat egymástól, a formulák utolsó tagjában látható: eltérő műveleteket írnak elő a választási függvények között. A különbség miatt nyilván nem vonhatjuk össze a két tulajdonságot, de a hasonlóság miatt az Arrow-feltételt is megőrzési tulajdonságnak tarthatjuk, olyannak, ami az örökletességre erősebb feltételt támaszt a Chernoff-axiómához képest. Más nézőpontból tekintve a dolgokra kicsit másfajta interpretációt is adhatunk az örökítés problémájára. Az egyszerűség kedvéért egyelemű halmazokra váltva: ha van egy m alternatívánk, amit előnyben részesítünk n-nel és o-val szemben, akkor ez a beállítódás nem szabad, hogy megváltozzon attól, hogy még egy elemet "beveszünk" az összehasonlításba. Vagyis nem lehetséges az, hogy egy p elem felvétele után már nem m-t preferáljuk n-nel vagy o-val szemben. Mindezt egy gyakran idézett gyakorlati példával szemléltetve: ha a csoki- és vaníliafagyik közül a csokit választjuk, majd ezután közlik velünk, hogy van még málna is, akkor – ha konzisztensek akarunk maradni – nem mondhatjuk másodjára, hogy inkább mégis vaníliát kérünk. [♦] Sen az általa definiált $\beta$-tulajdonságot a következő formában határozta meg.$\concept{(SEN-}\beta\concept{)}\defi\forall m\forall n((m, n \in C(S_1) \land \;S_1\subset S_2)\to (m\in C(S_2)\leftrightarrow n\in C(S_2)))$
Sen $\beta$-tulajdonsága (hun) – Sen's $\beta$-property (eng)
Sen javaslata értelmében ezt a minőséget úgy interpretálhatjuk, hogy ha a pakisztáni bajnokok közül legalább egy világbajnok is egyben, akkor az összes pakisztáni bajnoknak világbajnoknak kell lennie [Amart] Ha bővítjük az alternatívák halmazát, és az eredeti – szűkebb terjedelmű – halmaz legjobb (maximális) elemei közül egy a bővítés után is bekerül a legjobbak (maximálisak) közé, akkor a "korábbi" társaival is ennek kell megtörténnie. Sen definiált egy harmadik fontos tulajdonságot is, amit először $\gamma$-tulajdonságnak [SenA.] majd később a kiterjesztés konzisztenciájának nevezett el [SenA.] Sen az új kritériummal azt akarta biztosítani, hogy ha az alternatívák tetszőleges halmazaiból ugyanazt az elemet mindig kiválasztják, akkor a halmazok uniójából is ki kell választani.$\concept{(EC)}\defi \forall i (S_i\in \mathscr{S}\to (\bigcap\limits_i C(S_i)\subseteq C(\bigcup \limits_i C(S_i))))$
kiterjesztési konzisztencia (hun) – (basic) expansion consistency (eng) – Sen $\gamma$-tulajdonsága (hun) – kiterjedő (hun) – Sen's $\gamma$-propertiy (eng) – összehangoltság (hun)
Igazodva a Sen által korábban megadott interpretációk "műfajához", azt adhatjuk meg a $\gamma$-tulajdonság értelmezéseként, hogy ha valaki minden országban megnyeri az országos versenyt, akkor a végső összesítésben is nyernie kell, tehát a világbajnoknak is neki kell lennie. Sen megjegyezte azt is [SenA.] hogy ha csak a választási részhalmazok véges halmazaira fókuszálunk, akkor érdekes komplementaritást vehetünk észre az $\alpha$- és $\gamma$-tulajdonságok között. Mindez akkor válik különösen szembetűnővé, ha az $\alpha$-tulajdonság formuláját kicsit átalakítjuk.$\concept{(SEN-}\alpha\concept{)'} \defi \forall i (S_i\in \mathscr{S}\to (\bigcup\limits_i C(S_i)\subseteq C(\bigcap \limits_i C(S_i))))$
Sen $\alpha$-tulajdonsága (átalakítva) (hun) – Sen's $\alpha$-property (modified) (eng)
A komplementaritás szembetűnő: a fenti két formula csak annyiban különbözik egymástól, hogy a halmazműveletek egymás komplementerei egymásnak. A Sen által definiált tulajdonságok segíthetnek a racionális választással, választási függvénnyel szemben támasztott elvárások értelmezésében. A racionalitáskritériumok értelmezésében és meghatározásában azonban Marcel Richter hozzájárulása fontosabbnak mondható [Marce] Ő vezette be a kongruencia fogalmát, ami gyorsan az egyik legelfogadottabb racionalitáskritériummá vált. A kongruencia fogalmának kétféle (erős és gyenge) értelmezést is lehet adni – az alábbi módon.$\concept{(WCA)}\defi \forall S \in \mathscr{S}(\forall m\in S \land (\exists n \in C(S): \rel{R}_c))\to m\in C(S)$
gyenge kongruencia axiómája (hun) – Weak Congruence Axiom (eng)
$\concept{(SCA)}\defi \forall S \in \mathscr{S}(\forall m\in S \land (\exists n \in C(S): [\rel{R}_c]^{+}))\to m\in C(S)$
erős kongruencia axiómája (hun) – Strong Congruence Axiom (eng)
A kétféle tulajdonság meghatározása csak abban tér el egymástól, hogy amíg a gyenge kongruencia a Richter-reláció, addig az erős kongruencia a Richter-reláció tranzitív lezártjának való megfelelést írja elő a formulában. A racionalitáskritériumok között érvényes összefüggéseket tételszerűen nem mutatom itt be, Suzumura társadalmi választásokról szóló könyvében minden tételt kimond és be is bizonyít [Kotar] A könyvből viszont átemelek egy grafikus ábrázolást, amely szemléletesen mutatja a kritériumok közti kapcsolatrendszert. [♦]| $\rel{HARP}$ | $\leftrightarrow$ | $\rel{FR}$ | $\leftrightarrow$ | $\rel{QTR}$ | $\leftrightarrow$ | $\rel{AR}$ | $\leftrightarrow$ | $\rel{R}$ |
| $\updownarrow$ | ||||||||
| $\rel{SARP}$ | $\updownarrow$ | $\updownarrow$ | $\updownarrow$ | $\downarrow$ | ||||
| $\updownarrow$ | ||||||||
| $\rel{WARP}$ | $\leftarrow$ | $\rel{AA}$ | $\leftrightarrow$ | $\rel{(CA}$ + $\rel{SUA}$ + $\rel{GC)}$ | $\leftrightarrow$ | $\rel{(CA}$ + $\rel{GC)}$ | $\leftrightarrow$ | $\rel{CA}$ |
| $\updownarrow$ | ||||||||
| $\rel{WCA}$ | $\updownarrow$ | $\updownarrow$ | $\updownarrow$ | $\uparrow$ | ||||
| $\updownarrow$ | ||||||||
| $\rel{SCA}$ | $\leftarrow$ | $\rel{C} = \rel{C}^{R_C}_{cu}$ | $\rightarrow$ | $\rel{C} = \rel{C}^{R_C}_{so}$ | $\rightarrow$ | $\rel{C} = \rel{C}^{R_C}_{co}$ | $\rightarrow$ |
Választás és kontroll
Ugyan eddig nem reflektáltam rá, de ettől még tény, hogy a választásról eddig úgy beszéltünk, hogy az teljesen szabad volt, vagyis semmiféle kontrollt nem gyakoroltak fölötte. Nem volt sem külső, sem belső akadálya annak, hogy a választás előtt álló egyén saját késztetéseinek (és csak azoknak) megfelelően dönthessen. Pedig sokszor és sokféle módon elképzelhető, hogy van valamilyen kontroll a választásaink fölött. A kontroll egyik – belső – formája az önkontroll, míg a másik – belső vagy külső – formája a normatív kontroll. Már Thomas Schelling is használta, később Jan Elster is, és persze sokan mások az előzetes elköteleződés (precommitment) fogalmát, ami alatt valamilyen másodlagos preferencia kifejeződését, valamilyen szabadon mérlegelő tevékenység eredményét kell érteni, és semmiképpen sem szabad összekeverni a normatív elköteleződéssel, amelyben mindig van egy deontikus összetevő. Odüsszeusz és a szirének története szolgáltatja a jelenséggel foglalkozók kedvenc példáját, amikoris a hős vágyva arra, hogy hallja a szirének csodás énekét, de egyben vágyva arra is, hogy ne menjen utánuk a halálba, lekötöztette magát azért, hogy ne tudja megcselekedni azt, amiről a jelenben nem akarta, hogy a jövőben megtörténjék. Az előzetesen elköteleződés lényege tehát az, hogy a jövőbeni cselekvési lehetőségeket (vagy azok egy részét) kizárja valaki a jelenbeli döntésévelm, vagyis egy előzetes, ex ante döntéssel csökkenteni a majdani választási alternatívák számát [Klaus] Ezt a jövőre irányuló, jelenbeli elköteleződést úgy ragadhatnánk meg, ha a választás modelljébe beemelnénk az időt, de ezzel most nem próbálkoznék meg. Fontosabbnak tartom, hogy megpróbáljam azt modellezni, hogy miként lehetne a választás és normatív elköteleződés vagy csak röviden a választás és norma viszonyát leírni, jellemezni. Amartya K. Sen az 1990-as években fenntartásokat fogalmazott meg a racionális választás addigra egyeduralkodóvá vált paradigmájával szemben [SenA.] [Amart] és a társadalmi normák figyelembevételének fontossága mellett érvelt. Szemléletes példája a következő volt. A racionális választás paradigmája alapján – akármelyik racionalitáskritériumot is fogadjuk el – az alábbi két választást leíró választási függvényt inkonzisztensnek kell minősíteni:
$C(S_1)\equiv C(\{m,n\})=\{m\}$
$C(S_2)\equiv C(\{m,n,o\})=\{n\}$
Pedig könnyen kerülhetünk olyan helyzetbe, amikor teljesen racionális magyarázatot adhatunk arra, hogy miért választunk látszólag nem konzisztens módon, ha bővítjük a választható alternatívák halmazát. Gondoljunk csak arra – javasolta Sen –, amikor egy gyümölcsöstálban egyetlen alma van. Ekkor a választást értelmezhetjük úgy, hogy m jelenti azt, hogy nem vesszük el az utolsó almát a tálból, míg n-nel jelölhetjük azt az opciót, amikor elvesszük az almát. A tényleges gyakorlatban sokszor azt tapasztalhatjuk, hogy az emberek nem veszik el az almát, tehát m-t választják. És ha nem veszik el az almát, akkor azt azért teszik, mert érvényesnek tartják azt a társadalmi normát, amely tiltja az utolsó gyümölcs elvételét a tálból. Amennyiben viszont van egy másik alma is a tálban, amit a harmadik o alternatíva "felvételével" fejezhetünk ki, akkor ez a norma már nem tiltja valamelyik alma elvételét a kettőből. Elvehetjük akár azt is, ami előzőleg még tiltva volt, tehát ekkor választhatjuk az n alternatívát. Sen 1977-es cikkében már arról írt, hogy az eredeti konzisztenciaelvárásokat kétféleképpen is megsérthetjük, noha ilyenkor is racionálisnak érezhetjük a cselekvéseinket [Amart] [♦] Az egyik lehetőséget választófüggőségnek (chooser dependence), a másikat menüfüggésnek (menu dependence). Kotaro Suzumura és Walter Bossert a normativitás jelenségének megragadására, a normafüggő választás (norm-conditional choice) modellezésére azt javasolta, [♦] hogy az eredeti választási modellt ki kell egészíteni a normák tiltó hatását kifejező kivételhalmazokkal [Bosse] Ezt úgy tehetjük meg, hogy a normák által tiltott $m_k$ alternatívákat összekapcsoljuk adott választási halmazokkal $(S_k,m_k)$, és ezek uniójából létrehozzuk a norma alapú kivételhalmazunkat. Ha ezek után ezt a kivételhalmazt kivonjuk az eredeti választási halmazból, akkor azzal megkapjuk a normafüggő választási halmazunkat. Mindezt a következő formulákat írhatjuk fel.
$N=\{\bigcup \limits_k (S_k,m_k)\}$
tiltott alternatívák halmaza (hun) – kivételhalmaz (hun) – set of forbidden alternatives (eng)
$C^N(S,N) = C(S) \setminus N$
normafüggő választási halmaz (hun) – norm-conditional choice set (eng)
Miután előállítottuk a normafüggő választási halmazunkat, azt nyugodtan behelyettesíthetjük a "sima" választási halmaz helyébe, és azt használhatjuk tovább a már megismert formulákban, képletekben. Ezzel az egyszerű megoldással a racionalitáson alapuló döntés- és választáselméletbe "becsempészhetjük" a normativitás jelenségét.A társadalmi cselekvés típusai
"Az érzelmek kölcsönöznek irányultságot és értelmet az életnek, de egyúttal meg is gátolnak bennünket abban, hogy kitartóan ebben az irányban haladjunk."
[elste]
"Fölöttébb téves az a nézet, … miszerint fejlesztenünk kéne magunkban azt a képességet, hogy gondoljunk arra, amit éppen teszünk. Ennek pont az ellenkezője az igaz. A civilizáció azáltal halad előre, hogy gyarapítja ama fontos műveletek számát, amelyek végrehajthatók a róluk való gondolkodás nélkül. A gondolkodási műveletek a csaták lovasrohamaihoz hasonlítanak – számuk szigorúan korlátozott, megkívánják a friss lovakat, és csak a döntő pillanatokban vethetők be."
[A.N.W]
- értékracionális cselekvés
- célracionális cselekvés
- indulati-érzelmi cselekvés
- habituális (tradicionális) cselekvés
Indulati-érzelmi cselekvés
Amikor Max Weber kategóriatana második paragrafusában a cselekvések harmadik típusaként megadta az indulati-érzelmi cselekvést [weber] akkor nem adott sok túl sok támpontot a fogalom értelmezéséhez. A paragrafus definíciós részében semmi használható elem nincs, hiszen ott a megnevezésbe emelt fogalmakat ismételte meg újra, amikor azt állította, hogy a cselekvés lehet "indulati, különösen emocionális: ha tényleges indulatok és érzelmi állapotok … határozzák meg a cselekvést". A paragrafushoz tartozó magyarázó blokk harmadik bekezdésében írt ugyan egy tartalmas mondatot az indulati cselekvésről, de ezen kívül mást nem mondott."Indulati-érzelmi alapon cselekszik az, aki ténylegesen meglévő vágyait elégíti ki: bosszút áll, élvezetet szerez magának, odadást tanúsít, belefeledkezik a szemlélődésbe, vagy (mindegy, hogy egy az egyben vagy szublimált módon) levezeti az indulatait." [weber]
A kissé felszínes kezelésmód ellenére az persze nyilvánvaló, hogy Weber fontosnak tartotta ezt a cselekvéstípust. Ezt az a tény önmagában is igazolja, hogy Weber önálló típusként nevezte meg az indulat-érzelmi cselekvést. Ahhoz azonban, hogy ezt a cselekvéstípust egyértelműen el lehessen helyezni egy cselekvéselméleti modellen belül, szükséges néhol pontosítani, néhol kiegészíteni a weberi definíciót. Fontos ezt megtenni, mert egyfelől a pontosítások és kiegészítések után lehet egyértelművé tenni az indulati-érzelmi cselekvés viszonyát a többi motivációtípushoz képest, másfelől el kell tudnunk választani az érzelmi jelenségek igen széles körét az indulati-érzelmi cselekvések szűkebb tartományától. Amikor valaki beszámol egy indulati-érzelmi cselekvéséről, akkor gyakran ilyen kifejezésekkel érzékelteti a történteket: "elborult az agyam", "pánikrohamot kaptam", "semmit sem mérlegeltem", "elveszettem az ítélőképességemet", "önkívületi állapotba kerültem", "elragadott az indulat", "elveszettem a fejem", "megfeledkeztem magamról", "túláradó érzelem", "érzelemkitörés". Ez nem véletlen. Az indulati-érzelmi cselekvés lényege a "mindent elsöprő szenvedély". De mit is jelent ez a szenvedély, ez az önkívületi állapot, ez az elragadottság, ez az elvesztés, ez a megfeledkezés, ez a kitörés, ez a robbanás? Azt, hogy a cselekvő tudata egyetlen dologra irányul, a cselekvés egyetlen tényezőssé válik, minden más eltűnik a cselekvő tudatának horizontjáról. Intencionalitás van, valamilyen szintű tudatosság van, de nincs mérlegelés, és azért nincs, mert – a tudatot teljesen kitöltő – egyetlen dolgon nincs mit mérlegelni. Amikor a tudat kizárólag egyetlen tárgyra irányul, akkor beszélünk indulatról. Az érzelem, az affektivitás persze ennél sokkal többet jelent. A cselekvéstípusok közé besorolandó indulati-érzelmi cselekvéseket úgy kell értelmeznunk, hogy azok az érzelmi világunknak egy kis részét fedik csak le. Az érzelmi jelenségek egészét (affekció, affektivitás, affektus, emóció) három nagyobb részre bonthatjuk. Egyrészt vannak az indulati cselekvések, amikor felindulásról, indulatról, gerjedelemről, szenvedélyről beszélünk. Ezeket illesztem be itt a cselekvéselméleti modellbe. Ezek relatíve rövid ideig tartanak, és lényegük az indulat tárgyára történő kizárólagos irányulás. Pont a kizárólagosság miatt nem lehetnek ezek tartósak. Másrészt vannak a hangulatok. Ide olyan fogalmak sorolhatók, mint a kedély, kedélyállapot, kedv, mód, hajlandóság, de ide tartozik az empátia, szimpátia, antipátia, apátia, ellenszenv is. Ezek az érzelmi jelenségek már hosszabb ideig is képesek fennmaradni, viszont ezek már nem uralják kizárólagos módon a tudatunkat, bár erős befolyással lehetnek rá. Harmadrészt az érzelmek világába sorolhatjuk a (lelki)alkat, a lelkület, a mentalitás jelenségét is, és a kapcsolódó társfogalmakat: passziót, pátoszt, hajlamot, személyiséget, temperamentumot. Ezek a fogalmak persze nem rendelkeznek pontos határvonalakkal, és természetesen az affektív mező iménti felosztása sem mondható igazán egzaktnak. Az affektusmező három alosztálya elsősorban az időhöz való viszonyában rendezi el az affektív jelenségeket: az alapérzelmek nagyon rövid ideig (percekig, órákig) létező jelenségek, a hangulatok már hosszabb időszakon (napokon, heteken, akár hónapokon) át érvényeslő beállítódások, az affektív személyiségjegyek pedig korszakokon át tartanak (akár egy életen keresztül). Amennyiben az érzelmi jelenségeket felbontjuk, vagyis az időbeliség mentén affektív alosztályokat képzünk, akkor már kezelni tudjuk azt a többek által ellentmondásosnak tartott helyzetet, hogy ti. egyszerre tarthatjuk igaznak azt a két tézist, hogy az indulati-érzelmi cselekvések intencionálisak, a hangulatok és temperamentumok viszont nem. Amikor dühösek vagyunk, amikor félünk, mindig meg tudjuk mondani a haragunk, félelmünk tárgyát, de a tartós szorongás, a rosszkedv nem irányul semmire. Természetesen az affektivitás mindhárom területe ugyanolyan fontos részét képezi a mindennapi cselekvéseinknek. A cselekvéselméleti modellezés számára azonban a legszűkebb értelemben vett indulati-érzelmi cselekvés az igazán fontos. Amikor a cselekvéseinket ideáltipikus módon akarjuk jellemezni, akkor az affektív-érzelmi mező legbelsejében meghúzódó réteget kell feltárnunk. A hangulatok, illetve a affektív személyiségjegyek ettől még az érzelmi világunk ugyanolyan fontos részét képzik, mint az indulati-érzelmi cselekvések, csak amíg az utóbbiak elméleti modell egyik primitív (vagyis ontológiailag magasabb szintű) típusfogalmának kell tekintenünk, addig az előbbieket – fogalmi összetettségük miatt – más fogalmakból levezethető kategóriaként érdemes kezelnünk. Ha az érzelmi cselekvések eddig említett példáira gondolunk, akkor szembetűnő lehet két fontos vonásuk: egyfelől a tudatos ént bizonyos értelemben mindig passzív szerepben tapasztaljuk ilyenkor, másfelől az érzelmi megnyilvánulások együtt járnak testi reakciókkal, érzésekkel. Utóbbit önmagában is szépen jelzi az 'érzés' és 'érzelem' terminusok közti szoros etimológiai kapcsolat, de a magyar 'indulat', az angol 'emotion' terminusoknak a 'mozgás' fogalmához való kapcsolódása is ugyanezt fejezi ki. Noha az indulati-érzelmi cselekvés pont arról szól, hogy ilyenkor a tudatunkat egyetlen indulat, érzelem határozza meg, ez közel sem jelenti azt, hogy az érzelmekből hiányozna az intencionalitás. Nem beszélhetünk arról, hogy az indulat, az érzelem valamire irányul, hogy az érzelemnek tárgya van, ha nem feltételezzük, hogy az indulati-érzelmi cselekvésben inherens módon benne rejlik az intencionalitás. Ez persze nem jelenti azt, hogy az érzelem akaratlagos, szándékos lenne. A szenvedély nincs az akarat közvetlen irányítása alatt. Nem lehet akarni, hogy szeressünk, csodáljunk, tiszteljünk valakit vagy féljünk tőle, haragudjunk, irigykedjünk rá. "Lehet, hogy valaki kontrollálni tudja az érzelmei kifejezését, de az élményt magát nem …" [Zajon] Az is igaz, hogy elő lehet állítani tudatosan olyan helyzetet, amelyben jelentkezhetnek érzelmek, de ilyenkor a helyzet maga váltja ki az érzelmeinket, nem pedig a saját magunkra irányuló akarat. Ebben az értelemben az indulati-érzelmi és a racionális cselekvés valóban élesen szemben áll egymással, és az érzelmeket tényleg irracionálisnak kell tartanunk. Arra, hogy mire képesek az irracionális érzelmek (például a félelem), vagyis az indulati-érzelmi állapot mennyire figyelmen kívül képes hagyni minden racionális érvet, azt az esetet hozhatom fel kedvenc példámként, ami egy repülőgépen történt 1991-ben az USA-ban. A gép útját ugyanis meg kellett szakítani, és kényszerleszállást kellett végrehajtani vele, amikor olyan sok utas kezdett el összevissza rohangálni az ülések között egy egér miatt, hogy az már veszélyeztette a gép stabilitását [Epste] A teljes érzelmi mezőből nemcsak az időben tartósabb affektusokat kell kizárni a cselekvéselméleti modellezés jelen szintjéről, szükség van egy további szűkítésre is. Az érzelmeket abból a szempontból nézve is rétegekre bonthatjuk, hogy milyen mértékben tekintjük őket biológiai-neurológiai értelemben meghatározottnak, illetve az érzelmek működésén belül milyen szerepet tulajdonítunk a kognitív folyamatoknak, valamint a reflexió jelenségének. Ezzel kapcsolatban is többféle tipizálási javaslattal találkozhatunk a szakirodalomban. Az egyik felosztás szerint léteznek alapérzelmek és összetett érzelmek. Az előbbiek érzelmi primitíveknek tekinthetőek, amelyeket nem lehet visszavazetni más érzelmekre, nem lehet őket felépíteni fogalmi értelemben vett alacsonyabbrendű érzelmek segítségével. Az összetett érzelmek pedig több alapérzelem keverékeként tekinthetők. Ezt az osztályozási logikát a későbbiekben még előveszem, amikor az alapérzelmekkel kapcsolatos elméleteket mutatom be röviden. Vannak, akik pozitív, illetve negatív érzelmekről (büszkeségről, jóindulatról, együttérzésről, illetve rosszindulatról, irigységről, haragról) beszélnek aszerint, hogy – valamilyen morális mérce alapján – helyesnek vagy helytelennek tartjuk-e őket [Hirsh] Egy másik tipizálási javaslat szerint elkülöníthetünk alapérzelmeket és kognitív érzelmeket egymástól. Justin D'Arms és Daniel Jacobson a 'természetes érzelmek' és a 'kognitív hangolások' kifejezéspárt húzza rá erre a kettőségre [DArms] Az alapérzelmek (természetes érzelmek) evolúcióbiológiai mechanizmusok termékei, amelyek célja, hogy az életben maradás szempontjából kulcsfontosságú külső ingerekre reagáljanak, funkciójuk a környezeti ingerek monitorozása, figyelemkeltés veszély vagy rivális megjelenése esetén. A kognitív érzelmek (kognitív hangolások) az alapérzelmek alá besorolható – származtatott – érzelmek, amelyek már valamilyen jellemző és meghatározó kognitív összetevővel is rendelkeznek. Például a honvágyat mint egyfajta szomorúságot akkor érezzük, amikor távol vagyunk az otthonunktól, a gyászt mint szomorúságot egy hozzánk közeli ember halála váltja ki, a szerelem egy konkrét ember iránti érzelmek bonyolult keveréke, amiben van várakozás, öröm, bizalom (és még sok minden más). Az alapérzelmekből kevés van, a kognitív érzelmekből sokkal több áll rendelkezésünkre, hiszen bármilyen gondolatot összekapcsolhatunk egy természetes érzelemfajtával és ezzel egy új kognitív érzelemhez juthatunk. [♦] A kognitív érzelmek reflexiót kívánnak, és elsődleges testi ingerek nélkül is létrejöhetnek, vagyis az elméből is származhatnak [MrLsz] Amikor Antonio R. Damasio definiálja az elsődleges és másodlagos érzelmeket, akkor a tudatos reflektivitás minőségével különíti el az utóbbiakat az előzőektől [Anton] A másodlagos érzelmeket a minket ért élmények alapján alakítjuk ki, tehát tanulással jönnek létre, de ehhez nyilvánvalóan tudatra, megismerésre, relflexióra van szükség. Mérő László – az alapérzelmek és kognitív érzelmek mellett – az érzelmek harmadik nagyobb csoportjaként hivatkozik az ún. emberi érzelmekre, amelyek sajátossága, hogy ezek már a szelf jelenlétét is megkívánják [MrLsz] Amíg az alapérzelmek és a kognitív érzelmek (legalábbis egy részük) az állatokban is megjelenhetnek, addig az emberi érzelmek nyilván nem. Az érzelmi mező rétegekre bontásának indokoltságához lehet újabb adalék az a tény, hogy bizonyos érzelmek igenis tanultak, nem pedig velünk született reakciók. A New Hampshire-i Egyetem kutatói Gina Mireault és John Sparrow vezetésével csecsemőkkel végeztek kísérletet arra vonatkozóan, hogy a humort hogyan tanulják meg a gyerekek. A csecsemőket és szüleiket különböző helyzetekbe hozva, a videóra rögzített eseményeket elemezve arra az eredménye jutottak, hogy a csecsemők a szüleik reakcióiból tanulják meg, hogy mi a mulatságos, min hogyan lehet nevetni [GinaM] Bármennyire is érdekes és fontos az affektivitás többféle értelemben is sokrétegű jelensége, nem tudok és nem is akarok az érzelmi jelenségek mindegyik típusával foglalkozni. Elegendőnek tartom azt, hogy értelmezzem kicsit az indulati-érzelmi cselekvés jelenségét, valamint – abból a célból, hogy lehessen látni az utat, amin majd tovább lehet menni – kicsit foglalkozom még az alapérzelmek osztályozási és formalizálási kérdéseivel. Innentől kezdve amikor érzelemről, indulatról, affekcióról beszélek, akkor mindig ebben a – fent jelzett – leszűkített értelemben használom ezeket a terminusokat. Bár a pszichológusok elég régóta vizsgálják az érzelem jelenségét, egyelőre nem alakult ki konszenzus sem abban a kérdésben, hogy vannak-e alapérzelmeink, sem abban, hogy ha vannak, vajon melyek azok. A cselekvéselmélet számára talán nem is annyira lényeges ez a kérdés, még akkor sem, ha az nyilvánvaló, hogy az érzelmek beemelése a racionális döntések elmélete által dominált diskurzusba komoly előrelépésnek tekinthető. Az alapérzelmekkel kapcsolatos konszenzus hiánya ellenére érdemesnek tartok pár tipizálási kísérletet bemutatni, legfőkképpen olyanokat, amelyeket esélyesnek látok arra, hogy képesek lehetnek megkönnyíteni az érzelmi jelenségek logikai formalizálására törekvő kísérleteket. Az első ilyen osztályozási javaslat Robert Plutchiktól származik, aki átvette Darwin nézetét az érzelmekre vonatkozóan, miszerint az érzelmeknek adaptív funkciójuk van [Rober] Amikor Plutchik az alapérzelmeinket megpróbálta tipizálni, akkor feltette, hogy négyféle életprobléma van, amelyekkel szembe kerülve minden állat, így az ember is, megfelelő érzelmekkel reagál. Plutchik szerint az alábbi négy alaphelyzettel szembesülünk életünk során:- identitás
- temporalitás (reprodukció)
- hierarchia
- territorialitás
Plutchik mind a nyolc alapérzelemhez hozzárendelt még két-két olyan érzelmet is, amelyek közel vannak az adott alapérzelemhez csak éppen erősebb vagy gyengébb intenzitással rendelkeznek. Az ábra középpontjához közelebb feltüntett érzelmek nagyobb intenzitásúak, a középponttól távolodva pedig mindnen irányban gyöngül az érzelmek hevessége. A legkülső körön már olyan érzelmek is látszanak, amelyek két alapérzelem keverékeként minősíthetőek Plutchik szerint. A négy alaphelyezet és az alapérzelmek közti viszonyrendszer érzékeltetésére pedig álljon itt egy rövid felsorolás, miként kapcsolja össze adolgokat Plutchik: a szomorúság a szeretett személy elvesztését, a félelem fenyegetettséget, a harag akadályt, az öröm potenciális társat, a bizalom csoporttagot, az undor förtelmes tárgyat, a várakozás új territóriumot, a meglepődés hirtelen tárgyat jelent. Warren D. TenHouten tiszteletben tartva és elfogadva Plutchik alaprendszerét még tovább lépett, és az alapérzelmekből további másod- és harmadrendű érzelemfogalmat vezetett le az affektív birodalomról szóló könyvében [Warre] Izgalmas cikket publikált 2012-ben Hugo Lövheim az alapérzelmek biológiai meghatározottságával kapcsolatban [HugoL] Lövheim az általa megadott nyolc alapérzelmet aszerint tartja elrendezhetőnek egy háromdimenziós térben, hogy hogy viszonyul egymáshoz három neurotranszmitter aktuális szintje. Aszerint, hogy három neurotranszmitter, a szerotonin, a dopamin, valamint a noradrenalin szintje aktuálisan milyen értéken áll valakiben, Lövheim megmagyarázhatónak véli a nyolc alapérzelem keletkezését. Az alábbi ábra mutatja a neurotranszmitterek szintje és a lövheimi alapérzelmek közti összefüggést.
Lövheim tanulmánya még nagyon friss, elgondolásai épphogy csak bekerültek a tudományos diskurzusba, ezért nem árt némi óvatossággal kezelni az eredményeit, érdemes megvárni a szakma fogadtatását. Az azért elég nyilvánvaló, hogy amennyiben igazolódik Lövheim tézise, akkor az rendkívül erős alapot biztosít az érzelemelmélet számára. Mielőtt ismertetnék egy harmadik érzelemosztályozási javaslatot, bemutatok egy összegzést arra vonatkozóan, hogy az érzelmekkel foglalkozó legjelentősebb szerzők közül kik, milyen alapérzelmeket emeltek be saját elméletükbe. Warren D. TenHouten gyűjtötte össze és rendezte egybe ezeket az adatokat [Warre] tőle veszem át az alábbi táblázatot.
| Descartes (1647) | öröm | bánat | csodálat, szeretet, gyűlölet, vágy | |||||||||||
| Tomkins (1963) | félelem-rettegés | düh-őrjöngés | élvezet-öröm | szorongás-kín | érdeklődés-izgalom | meglepődés-megijedés | undor | szégyen-megalázottság | ||||||
| Plutchik (1980) | félelem | düh | öröm | bánat | várakozás | meglepődés | undor | bizalom | ||||||
| Osgood et al. (1975) | félelem | düh | (csendes) öröm | szorongás-bú | érdeklődés-várakozás | ámulat | unalom, undor | |||||||
| Arieti (1970) | félelem | őrjöngés | kielégülés | feszültség, (ét)vágy | ||||||||||
| Izard (1972) | félelem | düh | öröm | szomorúság | érdeklődés | meglepődés | undor | szégyen (szégyellősség, bűntudat), lenézés | ||||||
| Ekman (1980) | félelem | düh | boldogság | bánat | meglepődés | undor | ||||||||
| Emde (1980) | félelem | düh | öröm | bánat, szorongás | érdeklődés | meglepődés | undor | szégyen, szégyellősség, bűntudat | ||||||
| Scott (1980) | félelem | düh | gyönyörűség | magányosság, aggodalom | szeretet | |||||||||
| Panksepp (1982) | félelem | őrjöngés | remény | pánik | ||||||||||
| Epstein (1984) | félelem | düh | öröm | bánat | szeretet | |||||||||
| Trevarthen (1984) | félelem | düh | boldogság | bánat | ||||||||||
| Johnson-Laird, Oatley (1992) | félelem | düh | boldogság | bánat | undor | |||||||||
| Turner (2002) | irtózás-félelem | követelés-düh | kielégülés-boldogság | csalódottság-bánat | ||||||||||
| kínai tradíció | félelem | düh | boldogság | bánat | ||||||||||
| Darwin (1872) | félelem | düh | boldogság | bánat | meglepődés | undor | ||||||||
| Lövheim (2012) | félelem-rettegés | harag, düh | élvezet, öröm | érdeklődés, izgalom | meglepődés | lenézés, undor | szégyen, megalázás | |||||||
Átvéve Steunebrinkék megoldását én is OCC-vel hivatkozom a logikai formalizmus tartalmi forrását adó érzelemelméletre (a könyv szerzői nevének kezdőbetűi alapján). Az OCC-ben 22 érzelemre próbálnak kognitív magyarázó modellt adni. Az OCC-modell szerint az érzelmek háromféle intencionális tárgyra irányulhatnak: események következményeire, ágensek cselekvéseire, illetve tárgyak aspektusaira. Ha ezt a három fő szempontot kombináljuk olyan további szempontokkal, mint hogy melyik ágensről (a fokális személyről vagy a partnerről) van szó, relevánsak-e, kívánatosak-e vagy sem a következmények, akkor eljutunk az OCC-elméleten belül tárgyalt érzelmekig. A kérdés az, hogy miként lehet az ábrán látható struktúra elemeit egy logikai nyelv segítségével reprezentálni. A Steunebrinkék által kifejlesztett logika az ún. KARO ágensspecifikációs keretrendszerre épül [Meyer] [Meyer] Ezt azért érdemes igénybe venni, mert az érzelmek leírásához szükség van egyrészt ágensekre, másrészt a cselekvések értelmezéséhez kellenek a vélekedés, vágy, cél, terv, valamint a szándék fogalmai. Márpedig ezeket korábban mások már ellátták megfelelő logikai formalizmussal, amit érdemes újrahasznosítani, vagyis az érzelemlogika alapjául elfogadva egy alsó logikai rétegbe "betenni". Steunebrinkék első menetben "pontosítják", némileg átrendezik az OCC-modellt (ami tartalmilag nem jelent változást, csak a szintaktikai szempontokhoz könnyebben alkalmazható struktúrát biztosít a formalizálandó érzelemfogalmaknak). Ezután egy félig formális nyelven leírják az OCC-modell fogalmat. Azzal indokolják ezt a lépést, hogy ezen a szinten csak érzékeltetni szeretnék az OCC-modell fogalmainak szemantikáját, aminek alapján szabadon választható logika segítségével lehet formalizálni a modellt. Ezen a félformális tárgyalási szinten meg kell alapozniuk azokat a "segédfogalmakat", amelyek segítségével az érzelemfogalmakat definiálni lehet. Például fel kell venni a nyelvbe azokat a tulajdonságfogalmakat, amelyekkel értékeljük az események tárgyait (eseményeket, ágenseket/cselekvéseket, illetve tárgyakat). Amikor a jóság-rosszaság dimenziójában az események következményeit értékeljük, akkor azokat kívánatosnak (desirable) vagy nem-kívánatosnak (undesirable) tartjuk, amikor mások cselekvéseivel kapcsolatban ítélkezünk, akkor dicséretesnek (praiseworthy) vagy elítélendőnek (blameworthy) tartjuk azokat, amikor valamely tárgyat ítélünk meg, akkor vonzónak (appealing) vagy taszítónak (unappealing) véljük azt. A jóság (Good), illetve a rosszaság (Bad) fogalma alá tehát aszerint sorolható be három-három altípus (kívánatos, dicséretes, vonzó, illetve nem-kívánatos, elítélendő, taszító), hogy milyen típusú dologgal (eseménnyel, cselekvéssel, tárggyal) kapcsolatos. Ahhoz, hogy kifejezhessék az OCC-modellben leírt huszonkét érzelemet, Steunebrinkéknek – az itt érzékeltetett megoldások mintájára – tizenhét tulajdonságfogalmat kellett definálniuk. Az OCC-modell fogalmainak félig formalizált jellemzése után következik a szerzők két logikai nyelv segítségével is bemutatják, hogy lehet szabatosan formalizálni az OCC-modell érzelmeit. Először dinamikus episztemikus logikát használnak, majd a KARO-keretrendszert, ami a dinamikus logika, az episztemikus logika egyfajta keveréke, amit kiegészítettek még néhány, a cselekvések leírásához szükséges motivációs fogalmakat reprezentáló, modális logikai operátorral. Paul Ekman szerint az (alap)érzelmek elsődleges funkciója "felkészíteni" az egyént az interperszonális helyzetek gyors kezelésére a múltban sikeresnek, adaptívnak bizonyult megoldások, tevékenységek "felidézésével, újrahasznosításával" [PaulE] Ekman tehát – sok más pszichológussal együtt – osztja Darwin nézetét, miszerint az érzelmek, az affektív reakciók evolúciós eredetűek, és megtalálhatók az állatvilágban. Rovert B. Zajonc, egy másik híres érzelemkutató is hasonló módon vélekedett erről.
"Az affektív válaszkészség – eltérően a nyelvtől vagy a gondolkodástól – általánosan megtalálható valamennyi állatfajnál. Egy nyúl egy kígyóval szembekerülve nem vizsgálhat meg minden szóbajöhető lehetőséget a kígyóval kapcsolatban, hogy azokból sikeresen következtessen a kígyó támadására, annak időpontjára és irányára. A nyúl nem állhat meg a kígyó hosszáról, méregfogáról vagy bőrének geometriai mintázatáról elmélkedni. Ha a nyúl menekül, ezt jóval az emlékezeti jegyek mérlegelése előtt kell megtennie; valójában az előtt, mielőtt megállapította és tisztázta volna az elkövetkező mozgást, amire egy összetekert kígyó képes lehet. A futási elhatározásnak minimális kognitív emlékek alapján kell születnie." [Zajon]
Az érzelmek funkcióját más irányból is, más megközelítés alapján is lehetne elemezgetni. Jack Hirshleifer például a közgazdaságtan felől mutatott rá az érzelmek egy, a racionális, önérdekkövető cselekvő számára hasznos funkciójára [Hirsh] Hirshleifer szerint mind a pozitív, mind a negatív érzelmek szolgálhatnak arra, hogy segítségükkel a cselekvők kellő támogatást biztosítsanak fenyegetéseik és ígéreteik beteljesüléséhez. A közgazdasági szemléletmód persze meglehetősen ritkának mondható az érzelemkutatásban, így, bár érdekesek Hirshleifer gondolatai, nem fejtem ki őket alaposabban (azért sem tehetném meg itt, mert az értelmezésükhöz játékelméleti apparátus ismeretére is szükség lenne). Ahogy viszont azt már említettem, az érzelemkutatásban az (alap)érzelmek evolúciós felfogása széles körben elterjedt. Bizonyságul erre a következő idézet, amelyben Zajonc nyolvanas évek elejéről származó gondolatait harminc évvel később szinte visszhangozza Alan H. Goldman."A paradigmatikus vagy alapvető érzelmek funkciója az, hogy (átmenetileg) felváltsák a cselekvési lehetőségek mellett, illetve azok ellen szóló érvek, szokásos, racionális mérlegelését. A paradigmatikus érzelmek robbanásszerű motivációs állapotok. Adaptív erejük abban az eseményekre való reakciókészségükben van, amikor a racionális kalkuláció, annak akár a leginkább automatikus fajtája is, túl lassú. Durva, de nagyon gyors kognitív értékelésekre támaszkodva olyan korlátos viselkedéskészletet aktiválnak, amelyek evolúciós értelemben sikeresek voltak a múltban. … a félelem például a szokásos racionális mérlegelést kikerülve azonnali reakcióra késztet a veszély érzékelésekor. Ennek az adaptív ereje az azonnaliságban van. Több esetben sarkall hirtelen futásra, mint ahányszor valóban valós ok lenne a menekülésre, de adaptív szempontból nézve ez egy jó biztonsági stratégia. Jobb félni, mint megijedni." [AlanH]
A Goldman-idézet azért is érdekes, mert az érzelmi cselekvés több fontos összetevőjére találunk utalást benne. Itt az idő összeszedni és egy modellben bemutatni ezeket. Először is az érzelmeknek mindig van tárgya, mindig találnunk kell valamilyen intencionalitást, valamire való irányulást az indulati-érzelmi cselekvésekben. Az érzelemnek mindig van valenciája, érzelmi minősége, vagyis pozitív vagy negatív vonatkozása. Thomas Hobbes szerint a cselekvést megelőző gondolatokat "rendszerint törekvésnek nevezzük", és ebből kétféle irányultságot származtathatunk:"Ez a törekvés, amikor valamire irányul, étvágynak vagy vágynak nevezik, amikor valamitől távolodni igyekszik, általában ellenszenvnek hívják." [hobbe]
Voltaképp ez a bennünk levő törekvés, vagy másként: a dolgokkal való törődés adja a valencia, az érzelmi minőség alapját. [hobbe] Ha van valaminek valenciája, akkor, mivel valamilyen rendezési művelet áll a dolgok hátterében, ahhoz a jelenséghez könnyen lehet mértéket rendelni, amikoris mód nyílik intenzitást mérni. Így van ez az érzelmek esetében is: az érzelmeknek van intenzitása. Ebből fakad az érzelmek motiváló ereje. Az érzelmek egy fő funkciója valamely helyzetre, stimulusra adott megfelelő és gyors reakciókészség kialakítása. Ez talán legfőképpen abban nyilvánul meg, hogy az egyén úgy reagál a helyzetre, hogy egy korlátos viselkedési készletből automatikusan, mérlegelés nélkül kiválaszt egy cselekvési mintát és azt végrehajtja. Az érzelmi folyamatok talán legalaposabb leírását Nico H. Frijda adta meg [NicoH] Érdemes itt felidéznünk azt, ahogy Frijda egyetlen folyamatábrába sűrítetve jelenítette meg az érzelmi folyamatok legfontosabb összetevőit.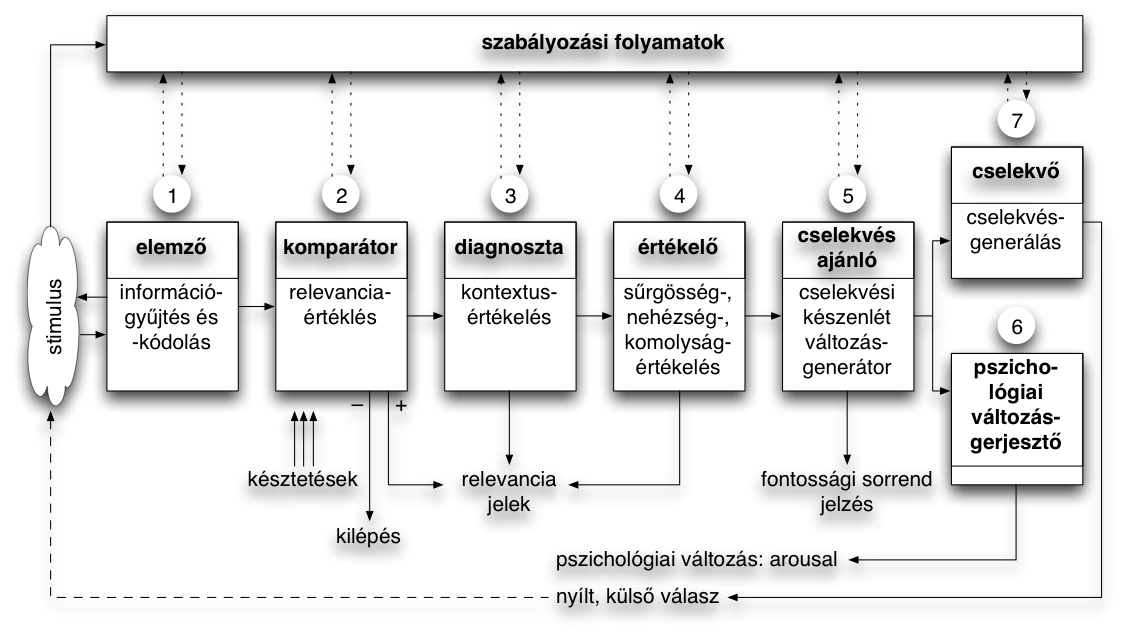
Minden érzelemnek van egy külső és egy belső előfeltétele. Egyfelől kell egy külső inger, másfelől kell egy belső jelzésrendszer, ami a késztetéseket, a fontosságokat jelöli ki az egyén számára. A külső inger, a stimulus az, ami elindítja az érzelmi folyamatot. A stimulust az elemző (1) részleg észleli és dolgozza fel, és erről jeleket ad tovább a komparátornak (2), ami összehasonlítja a stimulust mint új ingert az egyén számára belsőleg adott értékkészlettel, a késztetések (érintettségek, törődések) rendszerével. Az összehasonlítás eredményeként kijöhet az, hogy a stimulus érdektelen. Ebben az esetben a folyamat leáll. Amennyiben a komparátor azt jelzi, hogy a stimulus valamilyen törődést érdemel, akkor a folyamat vezérlése átkerül a diagnosztához (3), ahol a kontextus is felmérve egyfajta relevanciaérték rendelődik a stimulushoz (helyzethez). A értékelő egység (4) ezután a sürgősség, a bonyolultság és a komolyság dimenzióira figyelve meghatározza azt, hogy mennyire kell komolyan venni az éppen adott helyzetet. Ez alapján egyfelől megjelenik egy fontossági sorrend jelzés, másfelől a cselekvésajánló egység felkészíti az új – és azonnali – cselekvésre az egyént, ami megváltoztatja az egyén belső állapotát, arousal szintjét (6), illetve egy korlátos cselekvési készletből merítve egy viselkedési választ generál (7). Ezt a folyamatot természetesen rengeteg szabályozási mechanizmus kontrollálja, és ezek a részmechanizmusok az egyes belső egységekkel kétirányú kapcsolatrendszerrel vannak összekötve. A pszichológia területén a tudományos ismeretek közül a James-Lange elmélet biztos azok között van, amelyek szemben állnak a közgondolkodást uraló nézetekkel. A hétköznapi tudat számára egyáltalán nem tűnik kézenfekvőnek, hogy előbb vannak bennünk a testi változások, és ezek hatására érzünk majd érzelmeket magunkban – amiről a James-Lange elmélet legfőbb tézise szól. Ezt a tézist persze a tudományon belül is vitatják egyesek. Stanley Schacter és Jerome Singer 1962-es kísérletei szerint nem teljesen igaz a James-Lange tézis [Keith] Schacter és Singer kísérleti eredményei arról szóltak, hogy a kísérleti alanyoknak befecskendezett stimuláló anyag attól függően váltott ki eufórát vagy dühöt a páciensekből, hogy a milyen mintákat tapasztaltak a környezetükben más embereken, vagyis az érzelmek kialakulására kognitív folyamatok is hatnak. Az érzelmek testi vonatkozásaival kapcsolatban érdekes tanulmányt jelentetett meg 2013-ban Lauri Nummenmaa, Enrico Glerean, Riitta Hari és Jari K. Hietanen [Lauri] A kutatócsoport a kísérleti alanyok közreműködésével elkészítette az érzelmek kognitív hőtérképét. A kutatók különböző stimulusok (szavak, történetek, arcképek, filmek) segítségével érzelmeket keltettek a kísérleti alanyokban, majd arra kérték őket, hogy emberi alakot ábrázoló sziluetteken színekkel jelöljék be, hogy a testükön hol, melyik testrészükben észleltek erősebb érzeteket, érzéseket, illetve hol volt gyengébb szintje valamely érzetnek az átlagoshoz képest. Magasnak mondható korrelációs értékek mellett jöttek ki azok az eredmények, amelyek szerint a kísérleti alanyok a különböző típusú érzelmekhez nagyon hasonló, karakteres mintázatokat rendeltek. Mivel az eredmények a kísérleti alanyok saját jelentésein alapultak, ezért nehéz megmondani, hogy ezek a kognitív testi mintázatok, kognitív érzelmi hőtérképek mennyire a valós testi folyamatok modelljei, illetve mennyire a kognitív folyamatok kivetülései. Mindenesetre amíg – fizológiai mérések alapján – el nem készül a testünk valós érzelmi hőtérképe, ezek az adatok addig is érdekes mintát szolgáltatnak az érzelmek testi vonatkozásaival, a test és elme viszonyával kapcsolatos kutatások számára. Akármit is gondolunk a test és elme viszonyáról az érzelmek kapcsán, állásfoglalásunk nem kardinális a cselekvéselmélet modellje számára. A cselekvéselmélet számára csak a fontos, hogy létezik egy olyan cselekvéstípus, az indulati-érzelmi cselekvés, amely jól elkülöníthető a többi típustól, és ebből a szempontból tekintve másodlagos kérdés az, hogy miként is zajlanak az érzelmi folyamatok az emberen belül. Nagyon oda kell azonban figyelnünk arra, amit Frijda az érzelmi folyamatok talán legfontosabb összetevőjének tartott. Nem véletlen, hogy amikor Frijda az érzelemet többször is, többféle hosszúságban definiálta, akkor a legrövidebb meghatározásaként csak annyit adott meg, hogy az érzelem nem más, mint a "késztetések kielégítése" [NicoH] Ahhoz, hogy egyértelművé tehessem, mit is értett ezalatt Frijda, segíthet, ha – mintegy kontraszként – felidézzük, hogyan védte meg Jon Elster azt a tézisét, miszerint "érzelmekből áll az élet".
"Az érzelmileg semleges tapasztalatnak, ha egyáltalán elképzelhető, nem volna semmi értelme. Érzelmek nélküli teremtményeknek nem volna miért élniük, de életüknek véget vetni sem." [elste]
Elster szerint az érzelmek adnak értelmet az életünknek, mégpedig azáltal, hogy irányultságot adnak neki (ahogy ezt a fejezet első mottójaként szereplő idézetben Elster szószerint ki is mondja). A kérdés itt csak az, hogy mindez hogyan valósul meg. A kulcsmozzanat – ahogy azt már említettem – Frijda késztetés fogalma. Mivel a Frijda által használt angol 'concern' terminus sokjelentésű, így nehéz jó magyar fordítást találni rá. A 'késztetések' mellett lehetne az 'érintettség', a 'törődés', a 'törekvés', az 'értékirányultság', az 'érdeklődés', 'érdekeltség', sőt, akár még az 'érdek' terminusát is alkalmazni itt. Végül – a másik lehetséges terminus, az 'érintettség'-gel szemben – azért döntöttem az 'késztetés' terminusa mellett, mert az 'érintettség'-et idegenebbnek éreztem ebben a kontextusban, a 'törődés, törekvés' terminuspárban erősebb a kelleténél a szándékoltság minősége, az 'érdek' terminuscsalád pedig annyira erősen kötődik az önérdekkövető magatartással kapcsolatos diskurzushoz (egyébként alaptalanul!), hogy nagyon zavarónak éreztem volna ezt az erős konnotációt. Amikor Frijda a késztetés fogalmát bevezette, jelezte, hogy tudatosan válaszotta a 'motiváció' vagy a 'cél' fogalma helyett ezt az új fogalmat elmélete középpontjába, majd röviden definiálta is, mit ért ezen a kategórián."A késztetést olyan diszpozícióként definiálhatjuk, mint valamely helyzet megtörténte vagy be nem következése iránti vágyakozást." [NicoH]
Frijda a késztetést tehát vágyakozási diszpozíciónak tartja, amihez nyilvánvaló tisztáznia kéne, mit ért a vágy fogalma, de ezt nem teszi meg. Én korábban megpróbáltam tisztázni a fogalom jelentését (☜) itt abban az értelemben használom ezt a fogalmat, ahogy ott bemutattam. [♦] Ha valamiben érintett vagy érdekelt vagyok, ha valamivel törődöm, akkor valamilyen vonzást (vagy taszítást) érzek a szóbanforgó dologgal kapcsolatban. A vágy és taszítás fogalomkettősében ez a kétpólusosság, a valencia, a valamire való pozitív vagy negatív jellegű irányulás jelenléte a meghatározó mozzanat. Mindez persze nem tűnhet annyira meglepőnek. Az viszont már sokkal inkább, hogy ez az értelmezés mennyire egybevág azzal, amit Pierre Bourdieu gondol az érdek fogalmáról."Ahhoz, hogy megértsük az érdek fogalmát, látnunk kell, hogy az nemcsak az önzetlenség vagy az ingyenesség, de a közömbösség fogalmával is szemben áll. Közömbösnek lenni azt jelenti, hogy nem érint meg a játék, … érdektelen számomra. A közömbösség olyan axiológiai állapot, amely egyfelől a nem-preferálás etikai állapotának felel meg, másfelől olyan tudásállapot, amelyben képtelen vagyok különbséget tenni az felmerülő lehetőségek között. Ilyesmi volt a sztoikusok célja is: az ataraxia, az aggódásmentes állapot elérése. Az illusio az ataraxia tökéletes ellentéte: amikor a helyzetben és a helyzet által figyelmet, érdeklődést mutatunk a lehetőségek iránt." [Pierr]
Ez a bourdieu-i érdekfelfogás éles ellentétben áll azzal a ténnyel, ahogy a racionalitást, a racionális cselekvéseket annyian és annyiszor akarták (és akarják) az önérdek (self-interest), önérdekkövetés fogalmával megmagyarázni. Sokak szemében az érdekvezérelt cselekvés a tökéletes ellentéte az indulati-érzelmi cselekvésnek, így az érdek kategóriáját az érzelmi cselekvések középpontjába tenni értelmetlennek és ellentmondásosnak tűnhet. Pedig nem az. Ezt rövidesen bővebben kifejtem. Nyugodtan használhatnánk tehát az érdek fogalmát is itt, de praktikus okok miatt nem érdemes. Azért nem (de csak azért nem), mert az önérdek és az önérdekvezérelt cselekvés fogalmának gyakori használata során egyszerűen lekopott az önmagára való irányulást kifejező 'ön' szóösszetevő, és az érdek fogalmának értelmezése így valóban eltávolodott attól a felfogástól, amit fentebb Bourdieu kifejtett. Ez az átértelmez(őd)és annyira széleskörű, hogy nem érdemes szembe menni vele. A továbbiakban tehát a késztetés terminusát használva itt az idő bővebben kifejteni, mit is jelent pontosan az érzelmi cselekvés fogalma. Robert B. Zajonc fontos tanulmányát érdemes először megidéznünk. [♦] Bármennyire is korszakos állításokat fogalmazott meg Zajonc, az alapfogalmakat nem különítette el pontosan egymástól egymástól. A mondanivalója szempontjából ennek nem volt akkora jelentősége, de azért érdemes megemlíteni, hogy Zajonc sajnos összemosta az értékítélet, az attitűd, a preferencia és az érzelem fogalmait egymással. Ezt jól szemlélteti az a mód, ahogy az alábbi idézetben felcserélhetően használja ezeket a fogalmakat (egy, a preferenciákról szóló tanulmányban)."Az egyszer már kialakult értékítélet nem hajlamos a megváltozásra. Az érzelem fennmaradásával és az impressziók alakulását jelentősen meghatározó érzelemmel kapcsolatos vizsgálatok, és az a tény, hogy az attitűdök látszólag megközelíthetetlenek a kommunikatív meggyőzés számára, mind az érzelem hatalmas erejét és tartósságát tanúsítják." [Zajon]
Ez a terminológiai pongyolaság nem csökkenti annak a megkülönböztetésnek az értékét, amit Zajonc a kognitív és affektív ítéletek fogalomkettős bevezetésével teremtett meg. Miután alaposan bemutatta, hogy az érzelem (preferencia) alapú affektív ítéleteknek milyen sajátosságai vannak (elkerülhetetlenek, visszavonhatatlanok, a szelf által sugalmazottak, nehezen verbalizálhatóak, nem kell a gondolkodástól függeniük és külön válhatnak a tartalomtól, áthatolhatatlanok), Zajonc rámutatott a kétféle ítélkezés eltérő minőségére."A kognitív ítéleteket az ingerek jelen levő minőségei vezetik: 'Ez a macska fekete', 'A camambert és a brie puha érlelt sajt'. Ezek az ítéletek az ingerekhez rendelt I-skálákon születnek … Az affektív ítéletek azonban J-skálákon jönnek létre, ezek azok a skálák, amelyeken a különböző ingerek és a személy elképzelt preferenciapontjai együttesen helyezkednek el. 'Utálom ezt a fekete macskát' vagy 'A briénél jobban szeretem a camambert' – ezek az ítéletek a J-skálán vannak, így az affektív ítéletek mindig a szelfet érintik. Ezek határozzák meg az ítélkező álláspontját az ítélet tárgyához való kapcsolatában." [Zajon]
Zajonc itt a Clyde H. Coombs által bevezetett skálafogalmakra utal [Clyde] Ha viszont különböznek a kognitív és affektív ítéleteink, akkor meg kellene mondanunk, hogy miben is áll ez a különbség. Zajonc erre egy újabb fogalomkettőst vezet be, aminek értelmét akkor érthetjük meg igazán, ha gondolunk arra, hogy Zajonc azonos minőségeknek tekintette az érzelem és a preferencia fogalmait. [♦] " … nem alaptalan az a feltételezés, hogy sok döntésben fontosabb szerepe van az érzelmeknek, mint amit el akarunk ismerni. Gyakran áltatjuk magunkat, hogy egy racionális utat követünk és mérlegeljük az alternatívák pro és kontra érveit. De ez a konkrét esetben valószínűleg ritkán történik így. A leggyakrabban, amikor 'X mellett foglaltam állást', az nem jelentett egyebet annál, hogy 'kedveltem X-et'." Abból indult ki, hogy a kognitív ítéleteink arra támaszkodnak, hogy a világból érkező ingereket megkülönböztjük (képesek vagyunk a diszkriminálásra), amikoris minél pontosabb diszkriminációra vagyunk képesek, annál finomabb reakciókra van esélyünk. Azokat a tulajdonságokat, amelyek lehetővé teszik ezt a külvilág ingereinek feldolgozása során, Zajonc diszkriminandáknak nevezte el, és ezekkel állította szembe az affektív téleteink során használatos ingertulajdonságokkal, amikre ráhúzta az – általa alkotott – preferenda kifejezést. Utóbbiak azonban más minőséggel rendelkeznek az előbbiekhez képest."Azok az ingertulajdonságok, amelyek segítenek minket a tárgyak és események elkülönítése, felismerése, kategorizálása során, nem feltétlen használhatók ezen tárgyak értékelésekor. Ha pedig a dolgok így állnak, akkor léteznie kell egy olyan tulajdonságosztálynak, amely könnyen kombinálódik az érzelmekkel, és ezáltal lehetővé teszi számunkra, hogy elvégezhessük ezeket az értékeléseket, hogy megtapasztalhassuk a vonzódást, a taszítást, a kellemességet, a konfliktust és az érzelem további formáit, valamint biztosítsák számunkra, hogy megjelenhessenek bennünk ezek az érzelmi reakciók szinte azonnal a szenzoros élmények felbukkanása után. Ezek a tulajdonságok lehetnek egészen durvák, elmosódottak, globálisak, így könnyen előfordulhat, hogy nem szolgáltatnak elégséges alapot a legtöbb kognitív ítélet számára – akár még a legegyszerűbb megismerés-felidézés számára sem. Abból a célból, hogy megkülönböztethessük ezt a tulajdonságosztályt a diszkriminandumoktól, a továbbiakban preferendumnak fogom nevezni őket." [Zajon]
A Zajonc nézetét idővel egyre többen fogadták el. A követők közül Seymour Epstein elméletét emelném ki, aki ugyan új kifejezéseket vezetett be, viszont pontosabban definiálta voltaképp ugyanazt a kettősséget, amit már Zajonc is felállított. Epstein szerint kétféle megismerési, gondolkozási mód létezik, az intuitív-tapasztalati és a racionális-analitikai."Nem szűkölködünk a bizonyítékokban arról, hogy a mindennapi életben az emberek két, lényegileg különböző módon értelmezik a valóságot. Az egyiket nevezhetjük intuitív, automatikus, természetes, nem-verbális, narratív vagy tapasztalati módszernek, a másikat analitikainak, mérlegelőnek, verbálisnak vagy racionálisnak." [Epste]
Epstein sokféle címkét megengedhetőnek tart a két típusra való hivatkozásban, az elsőre legtöbbször az intuitív és a tapasztalati jelzőket alkalmazza, míg a másodikra elsősorban analitikai címkét ragasztotta, de gyakran hivatkozik rá racionálisként is. Ezzel némileg nehezíti annak a – maga által is vallott – tézisnek az elfogadtatását, miszerint mindkét megismerési, gondolkozási mód tartalmaz racionális elemeket – igaz, az analitikus többet, mint a másik. Az intuitív-tapasztalai rendszerünk ősi, az evolúció terméke, ami lehetővé tette elődeinknek a gyors reakciókészséget. Korábban is, most is nagyobb adaptivitást biztosít nekünk, hogy rendelkezünk intuícióval, ösztönös reakciókkat, zsigeri érzésekkel – például arról, hogy egy állatot szabad-e megközelíteni vagy a víz iható-e [PaulS] Idővel pedig kiépült a racionális-analitikai megismerési rendszerünk is, ami nagyon más elvek szerint működött a tapasztalai-intuitív rendszerhez képest. Epstein egy táblázatba összefoglalva mutatta be a kétféle megismerési, gondolkozási mód jellegzetességeit [Epste]| holisztikus | 1 | analitikus | ||||||||||||
| affektív: öröm-fájdalomorientált (mi jó) | 2 | logikus: értelemorientált (mi ésszerű) | ||||||||||||
| asszociációs kapcsolódások | 3 | logikai kapcsolódások | ||||||||||||
| a viselkedést a múltbeli tapasztalatokban gyökerező megérzések vezérlik | 4 | a viselkedést a történtek tudatos értékelése vezérli | ||||||||||||
| a valóság konkrét képekben, metaforákban, narratívákban képeződik le | 5 | a valóság absztrakt szimbólumokban, szavakban, számokban képződik le | ||||||||||||
| a feldolgozás gyorsabb, közvetlen cselekvésre irányul | 6 | a feldolgozás lassabb, késleltett cselekvésre irányul | ||||||||||||
| a változások lassabbak, az ismétlődő, intenzív tapasztalatokhoz igazodnak | 7 | a változások gyorsabbak, a gondolkodás sebességéhez igazodnak | ||||||||||||
| durvább differenciáltság, túlzó általánosítási hajlam, sztereotipikus gondolkodás | 8 | magasabbfokú differenciáltság | ||||||||||||
| durvábban integrált, disszociatív, érzelmi komplexek, kontextusfüggő feldolgozás | 9 | magasfokon integrált, kontextusközi feldolgozás | ||||||||||||
| passzív és tudatelőttes módon megtapasztalt: az érzelmeink irányítanak | 10 | aktív és tudatosan megtapasztalt: a gondolataink vezérelnek | ||||||||||||
| magától értetődő érvényesség, a tapasztalatban való hiten alapul | 11 | logikán és bizonyítékon alapuló igazolást követel | ||||||||||||
" … a másodlagos érzelmek által generált érzések sajátos esetei. Ezeket az érzelmeket és érzéseket tanulás révén összekapcsoljuk bizonyos szcenáriók előrejelezhető jövőbeni kimenetével. Amikor egy negatív szomatikus jelölő együtt jár egy bizonyos jövőbeni kimenettel, a kombináció vészcsengőként működik. Ha ehelyett egy pozitív szomatikus markert kapcsolunk össze a dologgal, az vonzerő jelzés lesz." [Anton]
A szomatikus markerek tehát úgy működnek bennünk, hogy erős élmények hatására elraktároztunk egy értékmozzanatot a valóság valamely összefüggéséről, és bizonyos feltételek teljesülésekor ezt az élményt testünk felidézi, azonnali testi jelzést ad, amely erősen befolyásolja, gyakran teljesen meghatározza döntéseinket. Ez funkcióját tekintve megegyezik azzal, amit Frijda mondott a késztetés (érdek) mint működési komponens értelméről. Az a damasioi gondolat, hogy a szomatikus markerek mint az affektív rendszerünk fontos összetevői elemi erővel hatnak a racionális gondolkodára is (előbbiek nélkül nem is létezhetne az utóbbi), itt most másodlagos (majd visszatérek rá a racionalitás tárgyalásakor). A szomatikus markerek azt építik be a késztetéseink, érdekeltségeink "affektív raktárkészletébe", hogy milyen irányú, polaritású, illetve milyen erősségű élmények értek a korábbi cselekvéseink során, és a későbbiek során az új ingerek felbukkanásakor az érzelmi folyamat mechanizmusai már ebből a folyamatosan változó jelzéskészletet használva működnek (ahogy azt Frijda leírta). Újra hangsúlyozom, hogy Damasio szomatikus marker elmélete nincs teljes fedésben egyik eddig bemutatott elmélettel sem, jelentősége is inkább a racionális gondolkodásunkra vonatkozó magyarázóerejében van, itt csak a szomatikus markerek és a késztetés/érdekeltség fogalmai közti hasonlóságra akartam rámutatni. Az a belső késztetés- és gátlásrendszer, amit Frijda a késztetés, Bourdieu az érdek, Damasio a szomatikus markerek fogalmával próbált megragadni, nem az indulati-érzelmi cselekvéstípushoz tartozik, és még csak nem is a teljes affektív mezőhöz vagyis az érzelmi jelenségek jóval tágabb köréhez, hanem az összes cselekvéstípushoz, vagy méginkább, a cselekvéshez általában. Nincs cselekvés vonzások és taszítások, késztetések és gátlások nélkül. Mérő László szerint Damasio szomatikus markerei másodlagos jelenségként épülnek rá a természet által bennünk kiépített alapérzelmekre úgy, hogy a megoldás egyáltalán nem értékelhető elegánsnak, meglepően barkácsolt jellegűnek mondható [MrLsz] Abban igazat adok neki, hogy a szomatikus markerek valóban rátelepülnek a már létező, biológiailag adott belső mechanizmusainkra, és ennyiben másodlagos jelenségek. A barkácsolt jelleget sem vitatnám. Csak azt látom másként, hogy mi is az az elsődleges rendszer, amire ráépülnek ezek második szinten. Szerintem nem az (alap)érzelemekre általában, hanem a biológiailag adott késztetéseinkhez, késztetésrendszerünkhöz képest másodlagosak. Az érzelmeinket is lehet szintekre bontani, de az másfajta felosztást jelent, mint a késztetések, érdekeltségek egész rendszerének két szintre osztása. Késztetéseinknek biztos van egy olyan rétege, ami biológiailag adott számunkra, és erre épülhetnek rá az életünk során a szomatikus markerek. Érdemes még megemlíteni azt, hogy a bennünk zajló érzelmi folyamatok eddig bemutatott jellegzetességeiből további következtetéseket vonhatunk le. Paul Slovic például rámutatott arra, hogy a tapasztalati-intuitív alapú megismerési és viselkedési üzemmódunk értelmezhető úgy is, mintha érzelmi heurisztikákat dolgoznánk és működtetnénk magunknak [PaulS] Az affektív mechanizmusok ismertetett vonásai, durvább, de előre kidolgozott, gyors válaszadás képessége könnyebbé és sok esetben hatékonyabbá teheti a viselkedést, mint az előnyöket, hátrányokat mérlegelő, összehasonlítgató, a memóriában emléknyomok után keresgélő racionális döntéshozatali mechannizmus. Különösen akkor van ez így, ha komplex döntéseket kell hozni, miközben a rendelkezésre álló mentális erőforrások valamiért korlátosak. Ilyenkor jöhetnek jól az slovici érzelmi heurisztikák. Az is igaz, hogy ha ezek a heurisztikák (affektív mechanizmusok, érzelemautomaták) a mindennapi életünk részei, akkor könnyen elképzelhető, hogy mások ezt kihasználhatják. Tudjuk jól, könnyen becsaphatóak, manipulálhatóak vagyunk. Sokszor (talán legtöbbször) azért, mert döntéseinkben a tapasztalati-érzelmi üzemmódra hagyatkozunk. Ezt ismerték fel és ezt használják ki a reklám- és marketinggépezetek. A viselkedésgazdaságtan területéről sok olyan példa hozható, amelyek azt szemléltetik, hogy hogyan képesek félrevezetni minket saját affektív-heurisztikus döntéseink (☜) Persze, látni kell azt is, hogy az érzelmi heurisztikáinknak vannak komoly, lényegükből adódó korlátai. A villámgyors reakció evolúciós eredetű követelményének azon az áron lehet(ett) megfelelni, hogy az affektív gépezetbe a cél teljesítéséhez szükséges elfogultságok, egyoldalúságok épültek be. Úgy tűnik, hogy az affektív rendszerünk arra lett tervezve, hogy a környezetünk kis mértékű változásaira tudjunk érzékenyen reagálni, a nagyobb léptékű változásokat már nem tudjuk jól kezelni. Slovic – kissé morbid – példája erre az, hogy nagyon éles különbséget tudunk tenni 0 és 1 ember halála között, de annál inkább érzéketlenné válunk erre, minél nagyobb számú haláleset közti különbséget kéne "értékelnünk". Nem tudjuk sehogy sem kezelni az 500 és 600 haláleset közti különbséget. Ugyanezt fejti ki Szent-Györgyi Albert is – csak kicsit érzékletesebb megfogalmazásban."A közös emberi szenvedés ugyancsak könnyen válik elvonttá. Engem személy szerint nagyon mélyen érint a szenvedés, a halál pedig felzaklat. Gyakran megkerülök egy háztömböt, hogy ne találkozzam egy temetési menettel; százezer ember halála azonban nincs rám semmilyen hatással. Csak mosolygok, mert képtelen vagyok megszorozni a halált vagy a szenvedést százezerrel. Ez nekem már csak puszta szám, absztrakció. Egy halál tragédia – százezer halál statisztika … " [Szent]
Tulajdonképpen ehhez hasonló jelenség az is, amikor a zsigeri érzéseket (éhség, szomjasság, addiktív sóvárgás) a jelenben erősnek érezzük, de a jövőbeni hatásukat, a jövőbeni cselekvéseinkre irányuló befolyásolási képességüket alábecsüljük. Egyáltalán: az időbeni folyamatokat, azok hatásait nem tudjuk igazán jól becsülni, előrejelezni. Ennek oka vélhetőleg az, hogy a tapasztalati gondolkodásmódunk a mostban, a jelenben zajló cselekvéseink megkönnyítésére jött létre. E korlátunknak egyértelmű példája az, hogy az egynapos differencia a ma és a holnap között sokkal nagyobbnak tűnik számunkra, mint ugyanaz az időtartamnyi különbség az 'egy év múlva' és az 'egy év plusz egy nap múlva' között. Ugyancsak és ugyanazért tudjuk nehezebben kezelni az időben lassan zajló változásokat az érzelmi rendszerünkön keresztül. Ezzel kapcsolatban Slovic meggyőző magyarázatot mutat be arra vonatkozóan, hogy a dohányosok miért kezdenek el a dohányzásba, miközben tisztában vannak annak káros hatásaival. Vitatható módon ugyan, de a dohányzást meg lehet kísérelni racionális alapon is megmagyarázni [huora] de a tapasztalati döntések figyelembe vételével más – és jobb – értelmezést is adhatunk. Amikor a dohányos a cigi után nyúl, akkor rövidtávú előnyöket, az azonnali élvezet lehetősége áll szemben a racionális rendszer által mérlegelhető hosszútávú kockázatokkal. Ebben az összehasonlításban az érzelmi heurisztika könnyen és gyakran felülkerekedhet a racionális mérlegelésen. Az érzelmekről szóló gondolatmenetem elején jeleztem, hogy az indulati-érzelmi cselekvések az affektív mezőnek csak egy részét képezik, és vannak olyan affektív jelenségek, amelyeket már nem lehet az indulat cselekvés terjedelmébe sorolni. A hangulatok, a temperamentumok is érzelmi jelenségek körébe tartoznak, de már nem jellemzi őket az az egydimenziós, egyfókuszú irányultság, és ebből adódóan csak korlátozott szándékosság van jelen vagy esetleg nem is érhető tetten az akaratlagosság. Az indulati-érzelmi cselekvések intencionálisak, de nem szándékoltak. Viszont minden érzelmi jelenség mélyén ott van az érdekeltségek rendszere, amelynek tartalmát, összetételét éppen az affektív mechanizmusok frissítik. Ez a mentális energiaközpont azonban nemcsak az affektív jelenségek számára, de minden más ugyanazt a szerepet tölti be.Habituális cselekvés
Nem véletlen, hogy Max Weber cselekvéstipológiájában utolsóként említi meg a tradicionális cselekvés típusát. Nem véletlen, mert Weber nem igazán szentel teret ennek a fogalomnak saját elméletén belül. Pedig sokkal több figyelmet érdemelne ez a cselekvéstípus, mert a hétköznapok világában nagyon sok esetben ez jellemzi a cselekvéseinket. Hogy ez így van, azt még maga Weber is elismerte – igaz, csak egy mondat erejéig. Bizonyságul erre, meg egyébként is, érdemes teljes terjedelmében felidézni azt, amit Weber erről a cselekvéstípusról írt. Nem sok.
A társadalmi cselekvés " … tradicionális: ha meggyökeresedett szokások határozzák meg a cselekvést."
[weber]
"A szigorúan tradicionális cselekvés – akárcsak a puszta reakciószerű utánzás … – teljesen a határán van annak – sőt, gyakran túl van azon –, amit egyáltalán » értelemhez« igazodó cselekvésnek lehet nevezni. Nagyon sokszor ugyanis csupán valamilyen homályos reagálást jelent a megszokott ingerekre, s a reakció irányát az egyszer meggyökeresedett beállítottság szabja meg. A megszokott mindennapi cselekvések többsége közel áll ehhez a típushoz, amelyet nemcsak azért kell fölvenni a rendszertanba, mert határesetet jelent, hanem azért is, mert … a megszokotthoz való kötődés különböző mértékben és többféle értelemben tudatosan is fenntartható. Ha ez a helyzet, a tradicionális cselekvés a 2. pontban tárgyalandó [értékracionális – Syi] típushoz kerül közel."
[weber]
" … az önmagukat meghatározott eredmény elérése érdekében szelektáló emberfajták nevelésének a fogalma a történelemnek is alapvető mozzanata: a látás tanítása, a járás, földmászás, lemenés, futás tanítása. Ez kiváltképp a higgadtság elsajátításában áll. Ez pedig elsősorban késleltetési mechanizmus, az összehangolatlan mozgások megakadályozása; a késleltetés pedig lehetővé teszi az összehangolt mozdulatok immár összehangolt válaszát, amelyek így az akkor megválasztott cél irányába hatnak. Az embert megrohanó nyugtalansággal szembeni ellenállás a társadalmi és mentális életben alapvető dolog." [mauss]
Van szépség és biztos, hogy van egy nagy adag igazság is abban, amit itt Mauss ír, de azt nem hiszem, hogy minden habituális cselekvés fogalma alá sorolható szabályszerűséget így lehetne és kellene megmagyaráznunk. Még kevésbé fogadható el vagy talán pontosabb úgy fogalmaznom, hogy még kevésbé lényeges számomra az, ahogy Mauss összekapcsolja a társadalmat és egyént ebben a jelenségben."A társadalomnak köszönhető, hogy a tudat beavatkozik. Nem a tudattalannak köszönhető, hogy beavatkozik a társadalom. A társadalomnak köszönhető, hogy létezik a kész mozdulatok biztonsága, a tudat uralkodik az érzelmen és a tudattalanon." [mauss]
Cselekvéselméleti nézőpontból csak első szinten azt kell tudnunk elkülöníteni egymástól, hogy milyen típusai vannak a cselekvésnek, és mivel a cselekvés fogalmát a hozzá kapcsolat szubjektív értelemmel, az intencionalitással magyarázhatjuk meg, ezért ezen a szinten nincs még szükségünk válaszolni arra, hogy miért is alakulnak ki, miért is léteznek egymás mellett az egyes cselekvéstípusok. E programhoz képest Pierre Bourdieu habitusértelmezése sokkal bővebb, sokkal ambíciózusabb, de ezt a kiterjesztést itt én szükségtelennek – és magam szempontjai szerint, sajnos, kicsit zavarónak – tartom. Újra hangsúlyozom: mindezt csak azért említem, mert szeretném indokolni, hogy az itt tárgyalt cselekvéselméleti modell számára miért "sok" Bourdieu habitusfogalma. Természetesen Bourdieu elemzése zseniális, mint ahogy frappánsak az olyan kifejezései is, mint "a habitus nem más, mint tudattalanított rutin" [Pokol] vagy "a habitus társadalmasított szubjektivitás", [Pierr] Bourdieu magára a fogalomra a következő meghatározást adta."A habituson olyan tartós és átvihető hajlamok rendszerét értjük, amely, valamennyi múltbeli tapasztalatot beépítve, minden pillanatban mint észlelési, értékelési és cselekvési minta működik. [Pierr]
Ebbe a definícióba tartalmilag nem tudok belekötni, bár nem tartom elég pontosnak. Mielőtt megadnám azt, hogy mit hiányolok belőle és hogyan javasolom kiegészíteni, szeretném megmutatni egy újabb idézet segítségével, hogy mi is az igazi kifogásom a buerdieu-i felfogással szemben. Bourdieu szerint a habitus egyszerre a társadalmi gyakorlatok eredménye (opus operandi), illetve a társadalmi gyakorlatok működésmódja (modus operandi), ebben az értelemben azok fenntartója. Ebben igaza van, mint ahogy a következő szövegrésszel sem tudnék, és nem is akarnék vitatkozni." … a habitus nem más, mint emberi természetté vált történelem, vagyis második természetté vált és így letagadott történelem. A "tudatalatti" valójában nem más, mint a történelem elfelejtése, ami abból fakad, hogy a történelem a habitusokba, e kvázi természetekbe ágyazza bele az általa létrehozott struktúrákat." [Pierr]
Bármennyire is elfogadom az idézet minden pontját, alkalmazhatóságát vitatom. Vitatom azon az alapon, hogy ez az értelmezés észrevétlenül átvisz minket a módszertani individualista megközelítésből egy olyan holisztikus szemléletmódba, ami egy cselekvéselmélet számára nem jelenthet adekvát nézőpontot. Igaza van (lehet) tehát Bourdieu-nek mindabban, amit mond, de minden gondolata inadekvát, ami nem a módszertani individualizmus talaján mozog. Márpedig amikor letagadott történelemről, osztályokról, természetté vált történelemről, szimbolikus hatalom érvényesítéséről az osztályhabitusokon keresztül, és ezekhez hasonló fogalmakról beszél Bourdieu, akkor már messze eltávolodik a módszertani individualizmus szintjétől. A bourdieu-i habitusfogalom egy másik értelemben is szélesebb terjedelmű ahhoz képest, mint ami elfogadható számomra. Az ő habitusfelfogása ugyanis nem érzékeny arra kérdésre, hogy milyen mechanizmusok révén alakul ki és marad fent a habitusba rögzült szabályszerűség. Számára oda tartozik az is, amikor az adott viselkedési mintázat valóban a puszta ismétlődés eredményeként jön létre, és az is, amikor a mintázat létét az attól való eltérést követő társadalmi szankció biztosítja. Weber fogalmaival leírva ugyanezt: a bourdieu-i habitusfogalom alá besorolható a weberi szokáshoz igazodó cselekvés, illetve a weberi rendhez igazodó cselekvés kategóriája egyaránt. Sőt, még a bourdieu-i értelmezésbe belefér az érzelmi cselekvések során beégetett értékelő jelzések, a szomatikus markerek teljes jelensége is. Ezt az értelmezést – saját modellem számára – túl tágnak tartom. És akkor most lássuk, hogy szerintem hogyan lehet értelmezni a tanult automatizmusok jelenségét, hogyan működnek valójában ezek a folyamatok, és hogyan lehet őket jellemezni a többi, részben hasonló jelenséghez való viszonyukban. Az egyik nagyon fontos vonása a habituális cselekvéseknek az, hogy van bennük egy olyan "gazdaságossági" mozzanat, ami elementáris erővel meghatározza a létüket és működésüket. Ezek az automatizmusok az agyunkat sokszor komoly mértékben tehermentesíteni tudják, és ez a képességük az, amivel a leginkább magyarázhatjuk az ilyen rutinok kialakulását és fennmaradását. Patkányokon, majmokon végzett mérések szerint a szokások kialakulása előtt a később szokásba rögzülő tevékenységsor még teljes agyi igénybevétel mellett zajlik, majd a szokás kialakulása után a rutinszerűen végrehajtható viselkedési elemek már nem dolgoztatják az agyat. Ez az agy számára rendkívül gazdaságos, mert egy ilyen viselkedési séma levezénylése sokkal kevesebb munkát igényel tőle. A rutineljárásokat az agy a legősibb területeken tárolja el, ahonnan már tudatos kontroll nélkül is irányíthat minket. Charles Duhigg megfogalmazásában: cselekvéseink jelentős részét "ciklikus agyi folyamatok", szokáshurkok (habit loop) vezérlik [Charl] E kifejezéssel Duhigg a viselkedést kiváltó jel, a végrehajtandó rutin és a tevékenység révén megszerezhető jutalom ciklikusságában megnyilvánuló automatizmust jelöli. [♦] A lényeg az, hogy a testünket gyakran trenírozzuk arra, hogy gépként hajtson végre valamilyen – többé-kevésbé bonyolult – mozgásfolyamatot. Vélhetnénk úgy, hogy egyáltalán nem véletlen az, hogy Mauss testtechnikáknak nevezte az általa elemzett tanult automatizmusokat. Ha valahol van valamilyen értelme valamilyen tevékenység ismételt megvalósításának úgy, hogy minél kisebb mértékben kelljen terhelni a tudatos agy feldolgozókapacitását, a figyelmet, akkor érdemes kialakítani ezeket az automatizmusokat. Ezek az automatizmusok a testi folyamatok esetén látványosak és egyértelműen működőképesek. Azonban koránt sincs arról szó, hogy csak testi mozgásokra lehetne ezt alkalmazni. Az előszóban már idéztem Neumann Jánost, aki azt mondta, hogy " ... a matematikában az ember nem megérti a dolgokat, hanem megszokja", aztán ennek a fejezetnek az elején olvasható az a Whitehead idézet, ami szerint a mentális folyamatainkban is rengetegszer rögzített, tehát automatikus gondolatmeneteken, hivatkozásokon keresztül haladunk előre, végül álljon itt még egy idézet e tárgyban."A szabályok létét az indokolja, hogy az emberek nem képesek erőfeszítések nélkül és hibátlanul alkalmazni az utilitariánus elvet; szükség van rá, hogy időt takarítsanak meg, és útjelzőket tűzzenek ki." J. Rawls [rawls]
A tanult automatizmusok nemcsak testi, de mentális folyamatok esetében is előfordulhatnak. Az eddig említett példákon túl gondoljunk csak az anyanyelven, majd az idegennyelven való megszólalás vagy az olvasás, az írás, a számolás, a kottaolvasás, a szakszövegolvasás és még ezernyi mentális készségre mint a tanult mentális automatizmusok példáira. Ezeket is rengeteg gyakorlással, trenírozással, belső szokáshurkok kialakításával építjük be magunkba, és miután már készségeinkké váltak, nem kell figyelmet szánnunk rájuk – vagyis minden ugyanúgy történik, mint a "hagyományos" testtechnikáink esetében. Bizonyos értelemben mondhatnánk, hogy nemcsak a habituális cselekvések tekinthetők automatizmusoknak, de az indulati-érzelmi cselekvések is – abban az értelemben legalábbis, hogy egyik cselekvéstípusban sincs mérlegelési, döntési lehetőség, s így nincs alternativitás sem a cselekvésben. Ehhez meg kell vizsgálnunk, mit is jelent az automatizmus fogalma. Mielőtt ezt megtenném, rá kell mutatnom egy nagyon lényeges különbségre a habituális és az indulati-érzelmi cselekvések között. Ha felidézzük azt a Mauss-idézetet, amelyben a testtechnikák értelméről volt szó (☜) akkor emlékezhetünk rá, hogy ott olyan kifejezések bukkantak fel, mint 'higgadtság elsajátítása', 'késleltetési mechanizmus az összehangolatlan mozgások megakadályozására' vagy 'nyugtalansággal szembeni ellenállás'. Mauss (és mindenki más, aki utána a habitusról értekezett) érték- és érzelemmentes automatizálásról beszélt, és ezáltal egy olyan vonást emelt ki és tartott jellemzőnek, ami pont "ellentétes" az érzelmek egész világával. Ez fontos különbség. A habituális cselekvések, a tanult automatizmusok – a jólismert ryle-i fogalmat használva – tudni hogyan jellegű készségek kialakítását és működtetését jelentik. Az indulati-érzelmi, illetve a habituális cselekvés abban tehát megegyezik, hogy nem a tudatos, szándékos irányítás, tehát nem a kontroll jellemzi őket, hanem inkább az automata jelleg, az viszont jelentős eltérés köztük, hogy az előbbiek az értékirányultságaink, utóbbiak a – tudni hogyan típusú – készségeink kezelésével kapcsolatosak. És akkor következzék az automatizmus fogalmának elemzése. Automatizmuson itt nyilván emberi cselekvések automatikus jellegét kell értenünk, amit érdemes szembeállítani egy másik cselekvéstípussal. Ha az automatikus cselekvés fontos minőségének érezzük a tudatosság hiányát, akkor ezzel szemben definiálhatjuk azokat a cselekvéseket, amelyek tudatosan vezéreltek. Daniel M. Wegner és John A. Bargh a kontrollált vagyis tudatosan irányított és az automatikus vagyis nem-tudatosan vezérelt folyamatokat elemezte egy tanulmányában [Wegne] amiből sokat tanulhatunk. Mielőtt bemutatnám, milyen tulajdonságokkal jellemezték Wegnerék a kontrollált folyamatokat, meg kell adnom azt, hogyan különítették el a folyamatok két típusát egymástól. A mérnökök világából jólismert fogalmakat átvéve azt mondhatjuk, hogy az automatikus folyamatokat a nyitott hurok, az előretáplálás (open-loop/feed-forward), [♦]- tudatos szándék irányul a folyamat révén elérendő célra,
- a kontroll érzése, észlelése,
- a várt eredmény eléréséhez szükséges "költséges" erőfeszítés,
- visszacsatoláson alapuló ellenőrzés a kimenet fellett.
- autonómia (miután a folyamat elindult, nincs szüksége tudatos irányításra),
- gyorsaság,
- hatékonyság (kevés figyelemkapacitásra van szüksége),
- előretáplált működésmód.
"… a kontrollt nemcsak pszichológiai folyamatotként kell érteni, de úgy is, mint egy érzést: annak tapasztalatát, hogy az ember valamit kontrollál vagy épp kontroll alatt van. A kontroll erőfeszítést követel meg, és pont ezen erőfeszítés elvárása teremt egy olyan érzést, hogy az ember csinál valamit, nem pedig csak hagyja történni a dolgokat. A tudatos kontroll során ugyanúgy maximálisnak tűnik a kognitív erőfeszítések tényleges ráfordítása, mint a mindent kitöltő erőfeszítés érzékelhető tapasztalata." [Wegne]
Az a tény, hogy a figyelem nagyon korlátos kapacitás, az információfeldolgozásban is "megköveteli és kitermeli" az automatikus folyamatokat [Shiff] [Schne] W. Schneider és R.M. Shiffrin kísérleteiben kiderült, hogy a kísérleti alanyok egy begyakorlási folyamat után tizenhat stimulus feldolgozásával is ugyanúgy megbirkóztak, mint amikor a kísérletek elején csak hat vagy kilenc stimulust kaptak, amiből az következik, hogy az információfeldolgozásban is vannak automatikus folyamatok. Feltehető a kérdés, vajon a két alapfolyamat jellemezhető-e, elkülöníthető-e aszerint, hogy miként viszonyulnak a többszörös folyamatok vezérléséhez, vagyis több folyamat létezése esetén a soros vagy párhuzamos vezérlés jellemzi-e őket. Tendenciaszerűen annyi mondható, hogy a nem-tudatos folyamat sokszor párhuzamos szálakból áll, míg a soros feldolgozás inkább tudatos folyamatokra jellemző, vagy fordítva: a tudatos folyamatokat inkább soros módon vezéreljük. Ez megintcsak a tudatos figyelem szűkös jellegéből kiindulva érthető meg. Amikor monitorozunk, mérlegelünk, döntünk, amikor egy folyamatot tudatosan vezérlünk, akkor mindig a maximális figyelmi erőfeszítés állapotában vagyunk, és ilyenkor nem tudunk egy másik tudatos folyamatot is ugyanilyen módon figyelemmel ellátni. Az automatizmus azonban nem jelenti sem a tudatosság, sem az intencionalitás teljes hiányát. David M. Armstrong a tudatosság alapvonásait, az elme, a szellem modelljét kereste, azt, hogy hogyan lehet megmagyarázni az intencionalitást, az elmét, a menális jelenségeket [David] Armstrong szerint a behaviorizmus rossz választ adott akkor, amikor kijelentette, hogy – karteziánus nézetekkel szemben – nincs szellem a dobozban, a mentális jelleg magában a cselekvésben fejeződik ki. Ezzel a magyarázósémával az a probléma ugyanis, hogy vannak olyan helyzetek, amikor a mentális folyamatok léteznek, de semmilyen viselkedésben nem reprezentálódnak: például magában (belül) mérges valaki. Armstrong kritizálta Gilbert Ryle – a diszpozíció fogalmára támaszkodó – magyarázatát is, aminek az a lényege, hogy az egyén nem viselkedik az adott módon, de diszpozicionált (beállított, előhangolt) úgy viselkedni (Armstrong ezt a minőséget a törvényekhez, normatív szabályokhoz hasonlítja). Ryle így írt a diszpozíció fogalmáról:"Ha valami egy diszpozicionális tulajdonsággal rendelkezik, akkor ez nem azt jelenti, hogy az illető dolog valamilyen különleges állapotban van, vagy hogy valamilyen speciális változáson megy át, hanem azt, hogy amikor valamilyen sajátos feltétel megvalósul, akkor szükségképpen vagy valószínűleg valamilyen sajátos állapotban lesz, vagy valamilyen speciális változáson megy át." [ryle:]
Armstrong szerint ez jó előrelépés, de kevés. Amikor mentális állapotban vagyunk minden külső viselkedési nyom nélkül, akkor valami csak történik ott belül, nem pusztán potencialitásról beszélhetünk."Amikor én gondolkozom, de a gondolataim nem valamely cselekvés végrehajtására irányulnak, akkor teljesen nyilvánvaló, hogy valami zajlik bennem, ami a gondolataimat eredményezi. Nem egyszerűen arról van itt szó, hogy beszélnék, cselekednék, ha bizonyos feltételek fennállnának, amelyek jelenleg nem állnak fent. Valami éppen akkor – a szó legerősebb, szószerinti értelmében véve – zajlik, végbemegy bennem, és ez a valami az én gondolatom. A ryle-i behaviorizmus tagadja ezt, ezért nem is kilégítő, nem is elfogadható az elme elmélete számára." [David]
Armstrong szerint a behaviorizmus akkor téved, amikor a mentális folyamatokat, az elmét egybemossa (azonosítja) a viselkedéssel. Ennél gyengébb kapcsolat is elképzelhető köztük. Armstrong javaslata: az elme, az egyéni mentális állapotok és a viselkedés között logikai kapcsolat létezik. A gondolat nem megfelelő feltételekre "váró" beszéd, hanem inkább valami az emberen belül, ami megfelelő körülmények között előidézi a beszédet. Ehhez viszont nem kell feltétlenül teljes tudatában lennek annak, amit éppen végrehajtunk. Armstrong az autóvezetést hozza fel például. Amikor az ember hosszú időn keresztül vezet, automatikussá válik szinte minden tevékenysége: gázt ad, fékez, forgatja a kormány, indexel stb. de mindezt nem tudatosan teszi. Pontosabban: a vezetése nagyobb részben nem tudatos, mert persze bizonyos értelemben azért használja a tudatát. A tudatosság teljes hiányában nem észlelné, hogy az út kanyarodik, nem forgatná el megfelelő mértékben a kormányt, és a kocsija az első kanyarban leszaladna az útról, vagy beleszeladna az előtte haladó autóba, ha nem észlelné, hogy a másik kocsi fékezett, és ne lépne rá ő is a fékre (a tudatos figyelem hiányában). Mégha a teljes tudatosság nincs is jelen, az intencionalitás akkor is megkérdőjelezhetetlenül benne van a folyamatban. És nemcsak az intencionalitást érhetjük tetten ilyenkor, de mindig kell találnunk valamilyen tudatosságot a folyamat valamely pontján, tipikus módon legalább a folyamat legelején. A vezetés, az írás, olvasás és minden más automatikus készségünk gyakorlás után válik automatikussá, de minden esetben valamilyen tudatos akarat van jelen az effajta folyamatok beindításakor. Amikor elindulok autóval, akkor tudatosan teszem ezt. És amikor váratlan, szokatlan esemény történik (például jégre futok a kocsival), akkor szükség lesz figyelemre, és egyből a tudat homlokterébe kerül az addig automatikusan végzett mozdulatok vezérlése. Az értelmezés kedvéért eddig élesen szembeállítottam egymással a kétféle folyamatot, ami sugallhatta azt, hogy ezek egymástól élesen elkülönülve működnek, működhetnek csak. Ez nem így van. Mégha egy ideáltipikus megközelítésben egyértelműen elválaszthatók is egymástól a kontrollált és automata folyamatok, a valóságban nagyon sok esetben egymásba fonódnak, összekapcsolódnak egymással. Wegnerék felsoroltak pár olyan kapcsolódási lehetőséget, ami a kontrollált és automatikus folyamatok között valósulhat meg, és amelyek valamilyen átmenetet, átalakulást eredményeznek az addigi folyamatokban.| többszálúság | párhuzamosan futnak kontrollált és automata folyamatok | |||||||||||||
| feladatátruházás | egy kontroll folyamat elindít egy automata folyamatot | |||||||||||||
| orientálás | egy automata folyamat elindít egy kontroll folyamatot | |||||||||||||
| rátelepülés | egy automata folyamat felülír egy kontroll folyamatot | |||||||||||||
| felülvizsgálat | egy kontroll folyamat felülír egy automata folyamatot | |||||||||||||
| automatizálódás | egy kontroll folyamat átalakul automata folyamattá | |||||||||||||
| megszakítás | egy automata folyamat átalakul kontroll folyamattá | |||||||||||||
Célracionális cselekvés
Kimondva-kimondatlanul, hivatkozva-hivatkozatlanul, de akik cselekvéselmélettel foglalkoztak az elmúlt, mondjuk, egy évszázadban, azok mindig kiemelt figyelmet szenteltek a racionális cselekvés és általában a racionalitás fogalmának. Persze nem is nagyon tehettek mást. Annyira a cselekvésünkhöz, sőt, emberi mivoltunkhoz tartozik a racionalitás minősége, hogy megkerülhetetlen. Nem lehet a cselekvésről beszélni nélküle. Ez így van még akkor is, ha a (cél)racionális cselekvést evolúciós értelemben megelőzi mind az indulati-érzelmi, mind a habituális cselekvés. Mondhatjuk azt is, hogy a racionalitás mechanizmusa ezekre "ül rá". A célracionális cselekvés esetében is Max Weber a kályha, tőle érdemes elindulnunk. Weber a következő meghatározást adta." … a cselekvést az határozza meg, hogy a cselekvő milyen viselkedést vár a külvilág tárgyaitól és más emberektől, és mennyiben képes e várakozásokat mint » feltételeket«, vagy mint » eszközöket« fölhasználni arra, hogy saját, racionálisan kiválaszott és mérlegelt céljait sikeresen elérje." [weber]
Mivel Weber kétféle racionális cselekvést különít el, ezért nyilván meg kell majd mutatni azt, hogy miben egyezik meg és miben különbözik a kétféle racionális cselekvéstípus. Ehhez elég lesz egyfajta racionalitásfogalmat felvenni a modellbe, és a különböző fogalmi összetevők, paraméterek eltérő értékeire rámutatva lehet majd elkülöníteni a racionális cselekvés kétféle altípusát egymástól. A racionalitás fogalmának meghatározása előtt azonban érdemes azt megvizsgálni, hogy miben tér el a kétféle racionális cselekvés az eddig tárgyalt másik két cselekvéstípustól, az indulati-érzelmi és a habituális cselekvéstől. A válasz egy szóval megadható, ami persze csak annyit jelent, hogy egy másik kifejezést használunk a racionalitás terminusa helyett. Az indulati-érzelmi és a habituális cselekvés során a cselekvő tudatában vagy nem volt ott a cselekvés intencionalitását adó értelem, mint a habituális cselekvés esetében, vagy egyetlen tárgyra irányult a cselekvő tudata. Mindkét esetben igaz az, hogy a cselekvőnek nem volt mit mérlegelnie. Ez a feltétel adja a lényegi közös vonásukat. Amikor ez a helyzet megváltozik, vagyis amikor a cselekvő tudatában több lehetséges szubjektív értelem is bekerül, melyek közül választania kell, amikor tehát alternativitás kerül a tudat elé, akkor beszélhetünk arról, hogy a cselekvő mérlegel. Amikor mérlegelünk, akkor alternatív cselekvési lehetőségeket vetünk össze egymással, melyek közül választanunk kell, és ez a választás, vagyis az általunk hozott döntést határozza meg, hogy végülis mit cselekszünk. Meg kell tehát vizsgálnunk a választás (döntés) fogalmát. Amikor mérlegelünk, választunk, a tudatunk saját tartalmaira irányul, ebben az értelemben a mérlegelés mindig magasabbrendű tudattevékenységet jelent, hiszen a mérlegelés mentális művelete más tudattartalmak közti választásként (tehát magasabbrendű fogalomként) értelmezhető. Ha egy cselekvésre azt mondjuk, hogy racionális, akkor ésszerűnek gondoljuk. A kérdés az, hogy mit is tartunk ilyenkor ésszerűnek. Sok mindenre vonatkozhat ugyanis az 'ésszerű' minősítés, a célok, az eszközök, a feltételek közti választás technikájára, a döntési folyamat egészére vagy annak valamely részére, a döntési mechanizmus "logikájára" vagy akár a választási folyamat végeredményére. Jack Hirshleifer azt hangsúlyozza, hogy a racionalitás elsősorban módszert, nem pedig eredményt jelent."A racionalitás instrumentális fogalom. Ha valaki saját céljait (preferenciáit) figyelembe véve megfelelő eszközöket (cselekvéseket) választ, akkor racionális; ha nem, akkor irracionális. A 'megfelelő' itt inkább a módszerre, mint az eredményre vonatkozik. A racionális viselkedés olyan cselekvés, amit a logika és az érvényesség más normái szerint mérlegelve hajtanak végre. A változásoknak köszönhetően pedig egy jó megoldás nem mindig vezet jó eredményhez." [JackH]
Hirshleifer nézetével egyetértve a továbbiakban a fenti racionalitásértelmezést próbálom meg alaposabban kibontani. Amennyire fontos fogalom a racionalitás, annyira sokféleképpen próbálják meg a fogalom jelentését megragadni, a definícióját megadni. Ez nyilván nem véletlen. Az eltérő szakmai nézőpontok máshová teszik a hangsúlyt. Az sem meglepő, hogy a racionalitás fogalmával a közgazdaságtan foglalkozott a legtöbbet, és a választásban megnyilvánuló racionalitás fogalmának kidolgozását nagyon komoly matematikai apparátussal támogatták meg az idők során (☜) Mégha egyoldalúnak, elfogultnak is tartom és ezért kiegészítendőnek vélem a közgazdasági értelmezést, ez természetesen nem jelenti azt, hogy ne tartanám szükségesnek bemutatni és a cselekvéselméleti modellbe beemelni ezt a fogalmat (pontosabban fogalomcsaládot). Szükség van azonban arra is, hogy kiegészítsük a közgazdasági értelmezést azokkal a szempontokkal, amelyeket más tudományágak, a filozófia, a szociológia képviselői tartanak fontosnak. [♦]Racionalitásértelmezések
a kontrollált folyamatokat zárt hurok, a visszacsatolás (close-loop/feedback) jellemzi. A zárt-hurkú, előretáplált folyamatokat Wegnerék a következő tulajdonságokkal jellemezték: John Broome filozófusként tágabb horizonton vizsgálta a racionalitás jelenségét [JohnB] Broome három racionalitásfeltételt kötött ki, melyek közül az egyikbe "belevetíthető" a közgazdászok által preferált értelmezés is (de erről majd később). Broome első feltételét az alábbi formulával fejezhetjük ki.$(\rel{B}_i(\phi) \land \rel{B}_i(\phi \to \psi))\to \rel{B}_i(\psi)$
modus ponens alkalmazása (hun) – applying Modus Ponens (eng)
A feltételt úgy értelmezhetjük, hogy ha az i személy hisz a $\phi$ állításban, és azt is hiszi, hogy a $\phi$ állításból "következik" egy másik, a $\psi$ állítás, akkor i-nek hinnie kell $\psi$-ben is. Ez nem jelent mást, mint hogy alkalmazza a modus ponens következtetési szabályt, vagyis képes következetések levonására, azaz képes a logikus gondolkozásra. Vannak, akik szerint ez kevés, a racionalitáshoz a logikai helyesség önmagában még nem elég. Evans-Pritchard a zandék törzsénél végzett vizsgálatai alapján azért különböztette meg a tudományos és a logikus gondolkozást, hogy rámutathasson, a törzsi társadalmak tagjai is logikusan (de még nem tudományosan) gondolkodnak."A tudományos képzetek azok, amelyek összhangban vannak az objektív valósággal mind a premisszáik érvényességét, mind az állításaikból levont következtetéseket tekintve … A logikai képzetek azok, amelyekben a gondolkodás szabályainak megfelelően az igaz premisszákból levont következtetések is igazak, a premisszák igazsága lényegtelen. … Egy fazék eltört égetés közben, valószínűleg a homoknak köszönhetően. Vizsgáljuk meg a fazekat, nézzük meg, tényleg ez volt-e az ok. Ez logikus és tudományos gondolkodás. A betegséget a boszorkányok okozzák. Egy ember megbetegedett. Kérdezzük meg a jósdát, melyik boszorkány a felelős érte. Ez logikus és tudománytalan gondolkodás." [E.E.E]
Evans-Pritchard megkülönböztetésével egyet lehet érteni, de ez az egyetértés még nem mond semmit arról, mit tartsunk racionálisnak, a logikus vagy a tudományos gondolkozást. Ha a tudományos gondolkodást követelnénk meg, azzal túl erős feltételt teremtenénk. Ráadásul a tudománytörténetből rengeteg olyan példát hozhatnánk, amikor egy tudományosan megalapozott premissza igazságáról kiderült annak hamissága, és ilyen esetekben egy darabig racionálisnak, majd utána nem-racionálisnak kellene tartanunk ugyanazt a hitet. Ezért én azt az értelmezést fogadom el, amely szerint – a most vizsgált kontextusban – a racionális feltételéül a logikus gondolkodás képességét kell megszabnunk. Evans-Pritcharddal szemben (és persze így Broome-mal egyetértve) Peter Winch és Steven Lukes is ezt az értelmezést fogadja el [WINCH] [LUKES] Broome második racionalitáskritériuma a cselekvés céljaira és eszközeire vonatkozó vélekedéseket és szándékokat kapcsolta össze. A feltételt így fejezhetjük ki formálisan.$(\rel{B}_i(M\to G) \land \rel{I}_i(G) \land \rel{B}_i(\rel{I}_i(M)\to M)) \to \rel{I}_i(M)$
szükséges eszközök akarása (hun) – wanting necessary means (eng)
A második broome-i feltétel annyit jelent, hogy ha az i személy úgy véli, hogy az általa megvalósulni kívánt G cél akkor teljesül a jövőben, ha az M eszköz is megvalósul, és i úgy gondolja, hogy M teljesülése az ő szándéktól függ, akkor i akarni fogja M megvalósulását. Magyarán: ha valamilyen célt el akarunk érni, és tudjuk, hogy a cél elérésének eszközeként valamit meg kell tenni, ami a mi szándékunkon múlik, akkor az utóbbit akarnunk kell megtenni. Ez a feltétel összeköti a célra irányuló cselekvések megvalósításának szándékát és a célok eléréséhez szükséges eszköz jellegű cselekvésekre irányuló szándékokkal. Broome harmadik kritériuma is a szándékainkkal kapcsolatos.$(\rel{B}_i(\rel{O}F)\land \rel{B}_i(\rel{I}_i(F)\to F))\to \rel{I}_i(F)$
krasia (hun) – krasia (eng)
A harmadik Broome-féle kritérium szerint ha i úgy véli, hogy meg kell tennie F-t, miközben úgy gondolja, hogy F-t csak akkor teheti meg, ha akarja megtenni, akkor i-nek akarnia kell megtenni F-t. Ez a feltétel a cselekvés szándékoltságát ragadja meg. A közgazdászok közül Harsányi János volt az, aki a szokásos, leszűkítő jellegű megközelítéshez képest jóval általánosabb szempontokra figyelembe véve foglalkozott a racionalitás problémakörével [Harsa] [Harsa] Egy 1976-os cikkében Harsányi abból indult ki, hogy a racionalitás szabályokhoz való következetes, koherens, konzisztens igazodást jelent. Nem fogadta el azonban a racionalitás cél-eszköz leírását vagyis a célok és eszközök viszonyrendszerén belüli, leszűkítő jellegű értelmezését mondván, hogy az nem foglalja magába a kritériumhoz igazodó viselkedést. Amikor a cél eléréséhez – például felmászni a legmagasabb hegyre – nem eszköz(ök)re, hanem kritériumra van csak szükség. A másik probléma a cél-eszköz racionalitás modellel az, hogy csak az adott cél eléréséhez szükséges alternatív eszközök mérlegelését teszi lehetővé, és ezáltal nem fedi le az alternatív célok közti racionális választás jelenségét, tehát nem lehet megmagyarázni, ha valaki egy adott cél helyett valami mást választ. Ezért van az, hogy ebből a modellből hiányzik a változás, a dinamika megragadásának lehetősége. Harsányi szerint ezen a ponton még előnyös a közgazdaságtani megközelítés hozadéka, mert a cél-eszköz alapú leírás helyett jobb a preferencia-lehetőség leírás modell, amely szerint a cselekvőnek vannak preferenciái, lehetőségei, és az ágens utóbbiakból választ az előbbiek alapján. Amennyiben az alternatív lehetőségek halmazából valaki kiválaszt egyet, akkor ez egyben azt is jelenti, hogy a többi lehetőséget nem választja, és a nem választott lehetőségekben rejlő kívánatosságpotenciált értékelhetjük a választási egyfajta költségeként is. A dolgokat így értékelve egyszerűen megmagyarázhatjuk azokat a jelenségeket, amikor valaki akkor is célt vált, ha az alternatív célokra vonatkozó preferenciái változatlanok maradtak, egyszerűen csak azért, mert az alternatívák költségei (még pontosabban: az effajta költségekről való ismeretei) megváltoztak. A preferencia-lehetőség modell magába foglalja mind a cél-eszköz, mind a kritérium-teljesítő modellt. Ha az ágens preferenciái megfelelnek bizonyos konzisztencia- és folytonossági feltételeknek, akkor ez a modell lehetővé teszi, hogy a preferenciáinkat hasznosságfüggvénnyel reprezentáljuk, és ebben az esetben a racionális cselekvés haszonmaximalizáló viselkedést jelent. Ezzel azonban nem tudunk mindenfajta racionalitást leírni. A döntéselmélet hozadéka az a fontos felismerés, hogy nem mindig, sőt, inkább ritkán cselekszünk biztos tudás birtokában vagyis a teljes bizonyosság (certainty) állapotában. Az életünket sokkal jobban jellemzi az a tény, hogy bizonytalanság (uncertainty) és kockázat (risk) mellett kell döntéseket hoznunk. Olyan racionalitásértelmezésre tehát van szükség, amely a bizonytalanság feltételei között is használható marad. Mielőtt megnéznénk, hogy tudunk ennek megfelelni, tegyünk egy rövid kitérőt a bizonytalanság fogalomkörével kapcsolatban. Először rögzítsük a három alapfogalom jelentését.$\concept{CERTAINTY}\defi \forall j(\modop{B}_i (p(A_j)=1))$
bizonyosság (hun) – certainty (eng)
$\concept{UNCERTAINTY}\defi \exists j(\modop{B}_i (p(A_j)\neq 1))$
bizonytalanság (hun) – uncertainty (eng)
$\concept{RISK}\defi \exists j \forall x(\lnot \modop{B}_i (p(A_j)=x) \land (0\leq x \leq 1))$
kockázat (hun) – risk (eng) – bizonytalanság (hun) – uncertainty (eng)
Akkor beszélünk bizonyosságról, ha a cselekvés során figyelembe venni kívánt, lehetséges kimenetre vonatkozó információink biztosak. Azt a helyzetet tarthatjuk bizonytalannak, amikor egyes kimenetek bekövetkezésének valószínűségét nem ismerjük. Ha létezik akár csak egyetlen kimenet, aminek megvalósulására nem tudunk még valószínűségi becslést sem adni, akkor azt bizonytalannak kell tartanunk. Kockázatról viszont akkor van szó, ha az egyes kimenetek bekövetkezésének valószínűsége (jól) ismert, kiszámítható. A lottózás során az egyes számok kihúzásának esélye pontosan ismert, tehát ezt kockázatnak kell minősítenünk. A kockázat és bizonytalanság itt megadott értelmezése – logikai szempontból tekintve – nem problémamentes, mert nem igaz az a sokszor hangoztatott nézet, miszerint a kockázat a bizonytalanság alárendelt fogalma lenne. Mivel azonban itt nincs szükségünk erre a tézisre, ezért nem is kell a modellbe felvenni. Azt viszont nem én állítom, hanem hazai közgazdászok (amit készséggel elfogadok), hogy a kockázat és bizonytalanság közti határvonalat tartalmilag is nehéz (vagy talán nem is lehet) pontosan meghúzni, és e fogalmak kezelését is sok esetben a pongyolaság, túlhasználtság jellemzi [Belya] [Belya] [Medve] [SzazJ] [Kovac]
"A modern közgazdaságtan egyik fundamentális észrevétele a kockázat és a bizonytalanság különbsége. A bizonytalanság melletti döntés kérdése alapvetően korlátozza a közgazdasági, így többek között a pénzügyi döntések lehetőségét. A kockázat feltárására, eliminálására számos lehetőséget tartalmaz az irodalom. Ugyanakkor, függetlenül attól, hogy ezeket milyen hatékonysággal hajtják végre a piaci szereplők, az inherens bizonytalansággal nem tudnak mit tenni. Bizonytalanság melletti döntés esetén az egyetlen lehetséges megoldásnak a 'több szem többet lát' módszere tűnik. Az optimális, igaz döntés lehetetlensége nem teszi szubjektívvá a rossz vagy előkészítetlen döntés fogalmát. A statisztikai módszerek által nyújtott, objektív kritériumok azonban nagyrészt illúziók, amelyek – minden kifinomultságuk ellenére – csak a múlt alapján következtetnek a bizonytalan, és így inherens módon ismeretlen jövőre.
Ugyanakkor a bizonytalanság és a kockázat megkülönböztetése is csak egy elmélet, amelynek az igaz vagy hamis volta nem vethető fel. Egyetlen döntési szituációban sem lehetünk biztosak abban, hogy kockázattal vagy bizonytalansággal állunk-e szemben, vagyis soha sem tudhatjuk előre, hogy az előrejelzések nem bizonyulnak-e végül igazaknak."
[Medve]
| $Alter_1$ | $Alter_2$ | |||||||||||||
| $Ego_1$ | 1,3 | 1,3 | ||||||||||||
| $Ego_2$ | 0,0 | 2,2 | ||||||||||||
- 1)] ha a játékosok elkülönülten páronként is találkozhatnak, akkor az első – mindegy, hogy kik között – létrejött találkozó szereplői vélhetőleg azonnal koalíciót formálnak és egyenlően elosztják maguk között a nyereményt;
- 2)] ha nincs mód szeparált találkozókra, és nincs elég idő a hármas találkozón arra, hogy kettős koalíció alakulhasson ki, akkor a három fél megegyezhet a hármas koalícióban, és harmadolhatják az összeget;
- 3)] ha a fentiekhez képest más feltételek adottak, akkor ilyen esetben bármilyen koalíció kialakulhat, de ezt nem lehet előre megjósolni.
- 1)]
az alacsony költségigény esetén követjük a pártatlanság és közjó elvét
Ha olyan helyzetekben vagyunk, amelyben nincs közvetlenül érdekeltségünk, akkor hajlandók vagyunk pártatlanok lenni, hajlandók vagyunk a köz érdekében, altruista módon fellépni, mindezt azonban csak akkor, ha nem túl megerőltető számunkra. A bírót kivonják az ügyintézésből, ha érdekeltsége van abban, de ha nincs, akkor képes részrehajlás nélkül ítélkezni – enélkül nem lenne működőképes közigazgatásunk. Elmegyünk szavazni annak ellenére, hogy racionális módon gondolkodva nem érné meg nekünk, és csak azért tesszük meg, mert kevés fáradságba kerül. - 2)]
konfliktus esetén sikeres lehet a pártatlan közvetítőkön keresztüli érdekaggregálás
A posztulátum értelme az, hogy ha ennek alapján egy harmadik – pártatlan – felet is bevonunk az érdekellentétes helyzetekbe, akkor a konfliktusban állók közötti kompromisszumkötést segítheti az új szereplő. Ez magyarázza meg a csoportérdek, osztályérdek, nemzetérdek fogalmát, jelenségét, de ez adja a morál alapját is, hiszen olyan megoldásokat lehet ezáltal találni a konfliktusok feloldására, amelyek minden ember érdekére tekintettel vannak. - 3)]
mások iránti elköteleződéseink korábbi racionális választásaink eredménye
Az ember személyes elköteleződései (a családtagok, a munkatársak, a barátok iránt) gyakran altruizmust eredményeznek. Ezek az elköteleződések azonban valamilyen racionális választás eredményeiként jöttek létre korábban. Miután az ember így vagy úgy elköteleződött, utána ezek az elköteleződések gyakran "altruista irányban" befolyásolják a mindenkori racionális döntéseket, de ez nem változtat azon a tényen, hogy az elköteleződések valamilyen korábbi racionális döntési helyzetben születtek. - 4)]
két fő motívumunk a gazdasági előnyök követése és a társas elfogadás igénye
Cselekvéseinket alapvetően két domináns érdekkel magyarázhatjuk. Az egyik alapmotiváció a gazdasági előnyök maximálása és a gazdasági veszteségek minimalizálása, a másik pedig a társas elfogadás iránti alapkésztetés. Cselekvéseink során mindig e két fő motívumból fakadó célok megvalósítására törekszünk.
Arkhimédeszi preferencia
A mérlegelés, a célracionális cselekvés fogalmának tárgyalásakor korábban már jeleztem, hogy ezek – bizonyos értelemben – másodrendű fogalomként értelmezhetőek, hiszen a mérlegelés folyamata azt jelenti, hogy célokat, eszközöket, következményeket veszünk figyelembe, vagyis több különböző szempontokat követve valamilyen döntést hozunk. A másodrendű minőség abban a mozzanatban érhető tetten, hogy amikor a mérlegelési folyamatban különböző szempontokat veszünk figyelembe és azok mentén hozunk részdöntéseket, akkor voltaképp belső késztetéseink, illetve ezek alapján a tudatossá váló preferenciarendezéseink határozzák meg a részdöntéseinket. A mérlegelés folyamatának egésze viszont nem jelent mást, mint ezen részleges belső szempontok (preferenciarendezések) egymáshoz viszonyítását, vagyis valamiféle másodrendű preferenciarendezés kialakítását az elsőrendű preferenciák felett. Mondhatjuk ezt a műveletet preferenciaaggregálásnak is, hiszen arról van szó, hogy több preferenciarendezésből kell egyetlen végső rendezést kialakítani. Ez az "elvárás" ugyanaz, mint a közösségi döntések elméletében leírt közösségi preferenciaaggregálás feladata (☜) A másodrendű preferenciarendezés persze többféle lehet. Én két fajtáját fogom bemutatni. A arkhimédeszi preferencia(rendezés) fogalmával kezdem azért, mert ezt a célracionális cselekvéshez kapcsolhatjuk. Vegyük át még egyszer, miről is van szó. Amikor a preferenciánkat fejezzük ki, akkor valamilyen szempont szerint valamely alternatívákon végrehajtunk egy preferenciarendezést. A szempontok tartalmával nem kell foglalkoznuk, viszont figyelnünk kell arra a mozzanatra, hogy könnyen előfordulhat (és gyakran elő is fordul), hogy ugyanazt az alternatívahalmazt több szempont szerint is értékelnünk (rendeznünk) kell. Ilyenkor merül fel a kérdés, hogy miként lehet egyszerre több szempontot is figyelembe venni. Azért fontos ez a kérdés, mert feltételezhető, hogy a különböző szempontok szerint más és más végeredményhez lehet jutni a rendezések során, miközben a mérlegelési folyamattól az egyértelmű döntést "várjuk el", hogy ti. a folyamat végén egyetlen kiválasztott cselekvési alternatíva álljon rendelkezésre a cselekvő számára. A következő fontos "technikai" kérdés, hogy milyen módon lehet a preferenciarendezést végrehajtani több elem (és/vagy több szempont) esetén. Ahogy már említettem, az egyik ilyen mód az arkhimédeszi preferenciarendezés alkalmazása. Az arkhimédeszi preferencia matematikai értelemben vett leglényegesebb tulajdonsága az, hogy nincs sem végtelen nagy, sem végtelen kicsi eleme, vagy másként: nincs ugrás az őt leíró függvényben. Ez persze már azt feltételezi (jelenti), hogy az arkhimédeszi preferencia folytonos függvénnyel reprezentálható. Amikor a preferenciát így tudjuk jellemezni, akkor alkalmazhatjuk rá a közgazdaságtan egyik központi kategóriáját, a hasznosság jenningsi fogalmát. Minden olyan esetben tehát, amikor a hasznosság fogalma kerül elő a cselekvések leírásában, feltételezhetjük/kijelenthetjük, hogy a cselekvők a döntési szempontjaikat az arkhimédeszi preferencia jellegzeteségének megfelelően veszik figyelembe. Az arkhimédeszi jelzővel tehát a cselekvők (döntéshozók) másodrendű preferenciarendezéseit minősíthetjük. Nem mindenkire és nem minden helyzetben jellemző ez az arkhimédeszi beállítódás, bár sokak szerint a modernizáció egyet jelent az archimédeszi preferencia elterjedtségének folyamatos növekedésével. Az arkhimédeszi rendezés dominánssá válásának és ezzel szoros összefüggésben a – következő fejezetben tárgyalandó – lexikografikus rendezés háttérbe szorulásának folyamatát Csontos László és társai "uralmi" tézisnek nevezték el [Csont] Ez a dominancia azt jelenti, hogy egyre több emberben, egyre több szempontra vonatkozóan kiterjed(t) az arkhimédeszi tulajdonság érvényessége. Amikor megfogalmazzák az "eladó az egész világ" szlogenjét, vagy amikor a reklámozásban való részvétellel szembeni ellenállás feladását fejezik ki a "van az a pénz, amiért korpás lesz a hajam" bonmot-val, akkor az arkhimédeszi tulajdonság terjedését, új területekre benyomulását példázzák. A kérdés itt az, hogy miként lehet formalizálni ezt a fogalmat. A relációelméleti részben bevezettem a sorrendezés vagy archimédeszi rendezés fogalmát (☜) az arkhimédeszi preferencia voltaképp ez alá a rendezési fogalom alá sorolható be. A közgazdászok az arkhimédeszi preferencia meghatározásakor a preferenciarelációt fogyasztói kosarakra (a matematikai reprezentáció szintjén vektorokra) alkalmazzák, tehát az összehasonlítást nem egyedi entitásokra, hanem entitások (mégpedig különböző típusú entitások) halmazaira vonatkoztatva fejezik ki. Erre a "módosított" preferenciarelációra írják elő az arkhimédeszi axióma érvényesülését, amely a következőképpen formalizálható (az arkhimédeszi preferenciarelációt az $\rel{R}$, az X és Y termékek különböző mennyiségeit $x_{i}$ és $y_{j}$ szimbólumokkal jelölve). [♦]$\concept{ARCHIMEDEAN\_PREFERENCE}\defi \forall i \forall j \exists k (\rel{R}((x_{i},y_{i}), (x_{j},y_{j})) \to \rel{R}((x_{j},y_{k}), (x_{i},y_{i})))$
arkhimédeszi preferencia (hun) – archimedean preference (eng)
A képlet azt fejezi ki, hogy bárhogy is állítunk össze két csomagot az X és Y termékekből, amelyek közül az egyik csomag ($x_{i},y_{i}$) többet ér a másiknál ($x_{j},y_{j}$), ha az Y jószág mennyiségét növeljük ($y_j$-t kicseréljük $y_k$-ra), akkor megfordulhat a preferenciareláció iránya, azaz ($x_{j},y_{k}$) csomag értékesebbé válhat az ($x_{i},y_{i}$) csomagnál. Az arkhimédeszi preferencia lényege az, hogy a szempontok összehasonlításakor, tehát másodrendben úgy járunk el, hogy nincsenek a szempontok között olyanok, amelyeket külön kellene kezelnünk a többiektől. Az egyes szempontokat természetesen mindig rendezi a döntéshozó, vagyis egyes szempontokat fontosabbnak, olykor sokkal fontosabbnak tart, mint a többieket, de mindig előállhat olyan konstelláció, amelyben a legerősebb szempont is hátrább kerülhet egy másik szemponttal szemben. Mindez jobban érthetővé válhat azután, hogy a másik fontos másodrendű preferenciarendezést, a lexikografikus preferencia fogalmát is bemutattam. Előtte azonban tárgyalnom kell az utolsó cselekvéstípust, az értékracionális cselekvés fogalmát.Értékracionális cselekvés
A weberi cselekvéstipológia negyedik eleme az értékracionális cselekvés kategóriája. Ez is nyilván racionális, mérlegelő cselekvés, és a legfontosabb kérdés az, hogy miben tér el a célracionális cselekvéstől ez a típus. Weber a következő meghatározást adta." … a cselekvés … lehet … értékracionális: ekkor a cselekvést egy meghatározott magatartásnak – pusztán mint olyannak, függetlenül attól, hogy sikeres-e – a feltétlen etikai, esztétikai, vallási vagy bármilyen más néven nevezendő önértékébe vetett tudatos hit határozza meg." [weber]
A definíció egyik fontos eleme, hogy Weber önértékbe vetett tudatos hitről beszél. Ebből számunkra az következik, hogy egyfelől ezt a cselekvéstípust a mérlegelés világába kell besorolnunk, másfelől a mérlegelést, a választást itt valamilyen értékelköteleződés határozza meg. Az érték jelenléte lényegi módon befolyásolja a mérlegelést. A fogalom meghatározásának másik lényeges összetevője az, hogy a mérlegelésnek nem a sikeresség a szempontja, hanem az értékelköteleződésnek történő megfelelés. Weber a definícióhoz fűzött magyarázó megjegyzései között ezt tovább egyértelműsíti, amikor összehasonlítja az indulati-érzelmi és értékracionális cselekvéseket."A cselekvés indulati-érzelmi és értékracionális orientációja abban különbözik egymástól, hogy az utóbbi tudatosan megszabja a cselekvés végső célját, és tervszerű következetességgel igazodik hozzájuk. Egyébként közös bennük, hogy a cselekvés értelmét nem a rákövetkező sikerben, hanem magában a meghatározott fajtájú cselekvésben látják." [weber]
Tudatos céltételezés és a célhoz való tervszerű igazodás – a mérlegelő cselekvés két legfontosabb eleme érhető tetten ebben az idézetben is. Mindez azonban nem jelenti azt, hogy az értékracionális cselekvést jellemző értékelköteleződésnek csak a célválasztásra lehet hatása. A mérlegelés során az eszközök kiválasztását is meghatározhatják értékválasztásaink. A mérlegelés egy újabb, különös fajtájáról van itt szó, és ezt a különös jelleget fogom feltárni a továbbiakban. Az értékelköteleződés fogalma alatt itt azt értem, amit a késztetésekről, vágyakról szóló fejezetben fejtettem ki (☜) Az érték az egyszerű késztetésekhez vagy vágyakhoz képest a vonzódás tudatosságában különbözik. Az értékeink úgy működnek, hogy amikor a mérlegelés során a lehetséges célok vagy eszközök között olyan alternatívák tűnnek fel, amelyeket értékelköteleződés köt minket, akkor azt az értékkötött alternatívát nem szabad figyelembe vennünk, vagy – épp ellenkezőleg – azt kell mindenáron végrehajtani. Ha egy férfi tervezi a hétvégi szórakozását, és mérlegeli, hogy a pénzéből mire mennyit költsön, akkor – ha számára a nőválasztás kérdése érték – eldönti, hogy kajára, piára mennyit adjon ki, de nem kalkulál azzal, hogy a szexuális szolgáltatás tervezett igénybevételének mennyi lesz az ára. A 'szerelmet nem lehet pénzért venni' értéke nem engedi meg számára azt, hogy prostituálttól vegye igénybe ezt a "szolgáltatást". Számára még csak szolgáltatásról sem is lehet beszélni. Az 'igazi háziasszony maga gyúrja a levesbe való tésztát' értékelkötelezettsége nem engedi meg, hogy a családi ebéd során bolti tésztát egyék a család. A cselekvési célt az értékelköteleződés jelöli ki, és nem számít, hogy mibe kerül. Nem lehet szempont, hogy vasárnap korábban kell felkelni és többet kell dolgozni, sok esetben még az sem számít, hogy a gyerekek valamiért már a bolti tésztát szeretik jobban (mert a menzán azt szokták, azt szerették meg). A kérdés az, hogy miként lehet ezt a kivételes szerepet megmagyarázni. Ebben segít minket a lexikografikus preferencia fogalma.Lexikografikus preferencia
Natura non facit saltum. A latin mondás szerint a természet nem szereti az ugrást. Az emberi természet más. A világhoz való viszonyaink között van olyanok, amelyeket nem tudunk folytonos függvénnyel reprezentálni. A lexikografikus preferenciarendezés művelete is ilyen. A döntéselméletben úgy mondják, hogy az arkhimédeszi preferencia kompenzatórikus jellegű, a lexikografikus preferencia pedig nem-kompenzatórikus. Kompenzatórikus egy döntési eljárás, ha bármelyik értékelési kritérium szerinti eredmény kompenzálható a többi szempont szerinti értékelésekkel, és nyilván a nem-kompenzatórikus eljárásban valamelyik kritériumra ez nem igaz [J.Dom] Szemléletes példa erre – bár a preferencia jelenségéhez való kapcsolata nem annyira egyértelmű – az az oktatási helyzet, amikor egy diák nem mehet tovább a következő félévre, ha nem teljesítette egy tantárgy minimálkövetelményét, mégha az összes többi tantárgyból jelest is szerzett. Ez úgy általánosíthatjuk, hogy előfordulhatnak helyzetek, amelyekben egy szempontot kiemelten kezelünk, és minden máshoz képest erősebbnek tartunk. Amikor a helyzetben releváns módon figyelembe lehet venni azt a szempontot, akkor az adott szempont kell, hogy meghatározza a döntésünket, és minden más szempontot figyelmen kívül kell hagyni. A közgazdasági szakirodalomba Nicholas Georgescu-Roegen vezette be a lexikografikus preferencia fogalmát [groeg] [groeg] A fogalom formális elemzésével Peter C. Fischburn foglalkozott a legtöbbet [Peter] [Peter] [Peter] [Peter] [Peter] [Irvin] [Irvin] [Steve] a fogalom elméleti alkalmazásáról, a vele kapcsolatos kísérleti eredményekről lásd: [lavoi] [colma] [elste] Említettem az arkhimédeszi rendezés dominánssá válásának tézisét [Csont] Itt nyilván e folyamatnak azt az ezzel párhuzamosan érvényesülő összetevőjét érdemes kiemelni, hogy az arkhimédeszi preferenciák terjedésével együtt a lexikografikus preferenciák fokozatosan háttérbe szorulnak. Ezt sokan értékvesztési folyamatként, az értékelvű magatartás eltűnéseként minősítik. Ebben a könyvben ennek a kérdésnek a tárgyalását nem tartom relevánsnak, de annyit azért jeleznék – a tendenciák létezét elismerve –, hogy az arkhimédeszi preferencia szerintem sosem terjedhet ki az életünk minden területére. Bizonyítani itt nem tudom ezt a tézisemet, nem is akarom, de szemléltetni azért szeretném, mégpedig azzal a reklámmal, amely egyébként az – arkhimédeszi preferenciát reprezentáló – bankkártyát próbálja népszerűsíteni. A Mastercard bankkártya 'Felbecsülhetetlen' szlogennel bevezetett reklámjában a kártyát magát azzal próbálják meg magasra értékelni, hogy a reklámban rámutatnak egy értékre (barátságra, családra, szerelemre, meghitt pillanatra stb.), ami "megfizethetetlen", majd a kártyát rögtön emögé pozícionálják. A reklámokat lezáró szlogen is ezt a kettősséget fejezi ki: "Van, amit nem lehet pénzért megvenni. Minden másra ott a MasterCard." Bármennyire is dominánssá válik az arkhimédeszi preferencia beállítódása, az értékekre való hivatkozást nem tudja nélkülözni. Nézzük meg tehát, hogy milyen módon tudjuk leírni a lexikografikus preferencia fogalmát. Ha van két termékünk (szolgáltatásunk vagy bármink, amire a preferenciareláció alkalmazható), akkor azok különböző mennyiségeit egy-egy vektorral reprezentálhatjuk: $(x_{1}, x_{2}, …, x_{i})$, $(y_{1}, y_{2}, …, y_{j})$, ahol $x_{i}$ az X jószág csökkenő nagyság szerinti sorrendbe állított $i.$ egyede, míg $y_{j}$ az Y jószág $j.$ példánya. Ebben az esetben a lexikografikus preferencia fogalmának formális meghatározását a következőképpen adhatjuk meg (a preferenciarelációt $\rel{R}$-fel jelölve). [♦]$\concept{LEXICOGRAPHIC\_PREFERENCE}\defi \forall j \exists i (j <{i} \to (\rel{R}(x_{j}, y_{j}) \land \rel{R}(y_{j}, x_{j}) \land \rel{R}(x_{i},y_{i})))$
lexikografikus preferencia (hun) – lexicographic preference (eng)
A formula értelmezésekor ki kell használnunk azt a feltételt, hogy a két jószágból vett különböző mennyiségeket – nagyság szerint csökkenő – sorrendbe állítva jelöljük $x_i$-vel és $y_j$-vel. Így a fenti képlet azt fejezi ki, hogy akármekkora mennyiséget veszünk is a két jószágból, azaz vehetjük akárhányadik ($j.$) elempárt a sorrendbe rakott termékekből, a két terméksor $j.$ elemeit megelőző párjaira még lehet döntetlen az állás köztük (ezt fejezi ki az $\rel{R}(x_{j}, y_{j}) \land \rel{R}(y_{j}, x_{j}$ részformula), de az $i.$ elemtől kezdve már az X termék a preferáltabb az Y-nal szemben ($\rel{R}(x_{i},y_{i}$). Ezt azt is jelenti egyben, hogy az X termék "összességében" kívánatosabb a másikhoz viszonyítva. A közgazdász értelmezés után megmutatom a lexikografikus rendezés matematikusok által kidolgozott modelljét is, mert egyrészt nagyobb kifejezőerőt, másrészt az általánosabb megközelítésmód miatt további hasznosítási lehetőségeket nyerhetünk vele. A modellt Andréka Hajnal, M.D. Ryan és P.Y. Schobbens dolgozta ki [HAndr] Andrékáék abból indulnak ki, hogy a preferenciarendezés fogalma nem elég a lexikografikus rendezés fogalmának definiálásához, szükség van a prioritás operátor bevezetésére. Azért, mert többféle szempont szerint is rendezhetünk dolgokat (autóvásárláskor figyelembe vehetjük az autó árát, gyorsulását, fogyasztását, vezethetőségét, színét, méretét, alakját stb.). Minden egyes szempont szerinti rendezés egy-egy preferenciarendezésnek felel meg, tehát sok rendezési relációnk is lehetséges. Ha pedig több szempont szerint kell rendezni ugyanazt az elemkészletet, akkor más és más sorrendek alakulhatnak ki a különböző szempontok (rendezések) szerint, amikor pedig szükség van arra, hogy a szempontok (rendezések) is valamilyen prioritást alakítsunk ki (vagyis valamilyen sorrendbe állítsuk őket. A rendezések rendezésének problémáját általánosítva túl lehet lépni az egyéni rendezések problémakörén, és felállítandó modell hatókörét ki lehet terjeszteni a közösségi döntések területére is. Amikor a többszerelős döntési folyamatokban egyetlen közösségi döntést kell hozni, akkor az egyéni preferenciákat kell egy közös preferenciába aggregálni. Matematikailag ezt ugyanúgy lehet kezelni, mint azt a helyzetet, amikor egy személy többféle szempontját kell egyetlen döntés során figyelembe venni. Andrékáék mindkét helyzetre (sőt, még továbbiakra is) érvényes modellt állítottak fel. Kiinduláshoz egy $\rel{R}$ tetszőleges reláció, valamint az $\underline{\rel{F}}$ teljes reláció és az $\underline{\rel{E}}$ üres reláció fogalmára van szükség (☜) Bár az $\rel{R}$-re preferenciarelációként hivatkozunk, a korábbi erős feltételeket (☜) itt nem követeljük meg. Nem kell feltételeznünk sem azt, hogy $\rel{R}$ reflexív, sem azt, hogy $\rel{R}$ tranzitív legyen. Semmilyen tulajdonságot nem kell megkövetelnünk $\rel{R}$-től. A "legalább olyan jó" (jobb vagy ugyanolyan jó) jelentés mentén értelmezett $\rel{R}$ relációra támaszkodva a következő további relációkat vezethetjük be.$\rel{R}(m,n)$
$\rel{R}$ a legalább olyan jó (jobb vagy ugyanolyan jó; jobb vagy közömbös) reláció; $\rel{R}$ a $P=\{m,n, …,o\}$ (világ)állapotok halmazán van értelmezve.
$\overline{\rel{R}}(m,n)\defi\lnot \rel{R}(m,n)$
$\overline{\rel{R}}$ a rosszabb (se nem jobb, se nem közömbös) reláció; $\overline{\rel{R}}$ az \rel{R} negáltja.
$\concept{BETTER}(m,n)\rel{R}^{<}(m,n)\defi\rel{R}(m,n)\land\lnot \rel{R}(n,m)$
$\rel{R}^{<}$ a jobb (szigorúan jobb; erősen preferált; szigorúan preferált) reláció; $\rel{R}^<$ aszimmetrikus.
$\concept{INDIFFERENT}(m,n)\rel{R}^\equiv(m,n)\defi\rel{R}(m,n)\land \rel{R}(n,m)$
$\rel{R}^\equiv$ a közömbös (indifferens) reláció; $\rel{R}^<$ szimmetrikus.
$\concept{INCOMPARABLE}(m,n)\equiv\rel{R}^\#(m,n)\defi\lnot \rel{R}(m,n)\land\lnot \rel{R}(n,m)$
$\rel{R}^\#$ az összehasonlíthatatlan (inkompatibilis) reláció.
Az univerzális és üres reláció, valamint a fenti preferencia-vonatkozású relációk között megállapíthatóak a következő összefüggések:$\overline{\underline{\rel{F}}}=\underline{\rel{F}}^{<}=\underline{\rel{F}}^\#=\underline{\rel{E}}^{<}=\underline{\rel{E}}^\equiv=\underline{\rel{E}}$ $\underline{\rel{F}}^\equiv=\underline{\rel{E}}^\#=\overline{\underline{\rel{E}}}=\underline{\rel{F}}$
Ezekután az $\rel{R}(m,n)$ preferenciarendezés mintájára vegyük az $\{\rel{R}_v(m,n)\}_{v\in V}$ preferenciarelációk valamely halmazát (ahol $m,n \in M$). A preferenciarelációinkra legyen adott még egy $|V|$-edrendű < (szigorúan részben rendezett) prioritás operátor is.$<(\rel{R}_x(m,n),\rel{R}_y(m,n))\equiv<(x,y)\equiv x<{y} \defi \concept{STRICT\_PARTIAL\_ORDER}(x,y)$
prioritás reláció (hun) – priority relation (eng)
A formula azt fejezi ki, hogy a prioritás reláció szigorú részben rendezés, azaz a reláció reflexív (☜) tranzitív (☜) és antiszimmetrikus (☜) Ekkor a $\{\rel{R}_v(m,n)\}_{v\in V}$ preferenciarelációk halmazán, azok kombinációjaként értelmezett $\langle\rel{R}_v(m,n)\rangle_{v\in V}$ rendezett $|V|$-es, amit innentől $lpref(m,n)$ lexikografikus preferenciarendezésnek nevezünk, így definiálható.$\langle\rel{R}_v(m,n)\rangle_{v\in V}(m,n)\equiv \concept{LPREF}(m,n) \defi \forall i\in N (\rel{R}_{v(i)}(m,n) \lor \exists j \in N(<(j,i) \land \rel{R}_{v(j)}^<(m,n)))$
lexikografikus rendezés (hun) – lexicographic order (eng)
A formula egy diszjunkció. Az első komponens akkor lesz igaz, ha az aggregátum összes eleme ($\rel{R}_x(m,n)$) ugyanúgy rendezi el a két elem (m és n) viszonyát. Ennek kiderítéséhez végig kell menni az aggregátumba bevont összes preferenciarendezésen, hiszen univerzális kvantor zárja le ezt a részformulát. A képlet második összetevője megadja a kiértékelési folyamat gyorsabb lezárásának lehetőségét (ebben az értelemben rendkívül praktikus szabálykomponenesnek minősíthetjük). A diszjunkció második eleme ugyanis azt rögzíti, hogy ha elindulunk a prioritási sorba állított preferenciarendezések kiértékelésében, és ezek között van olyan reláció (a prioritási sor $y.$ pontján), amely az összehasonlított két elem (m és n) közül az egyiket szigorúan preferálja a másikkal szemben ($\rel{R}_y^{<}(m,n)$), akkor ez a tény eldönti az teljes lexikografikus rendezést is (az éppen adott prioritási ponton szigorúan preferált alternatíva vagyis az m javára). Értelmezéséhez segíthet, ha a szótári rendezés példájára gondolunk. A szótárakban (lexikonokban) szavakat kell sorba állítanunk, ezeket jelöljük itt az $m,n$ változókkal. A < prioritás operátor itt a betűk szavakon belüli pozícióinak sorrendjét határozza meg (európai írásmód esetén balról jobbra halad a sorrend). A $\rel{R}_x(m,n)$ preferenciarelációink mind megegyeznek, és az ábécé szerinti rendezést jelentik. Annyi preferenciarelációnk van ($|V|$), ahány betűje van a szótár legtöbb betűből álló szavának. Minden szó tetszőleges $x.$ pozíciójában a $\rel{R}_x(m,n)$ preferenciareláció alapján meg tudjuk mondani, hogy az ott található betű alapján az adott szó mely szavakat előz meg, mely szavak vannak előtte, illetve mely szavakkal van azonos helyzetben (amikor ugyanaz a betű szepel az $x.$ pozíción). Ez azonban kevés a lexikon szavainak sorrendbe állításához. A végleges rendezést a < prioritás operátor segítségével lehet csak kialakítani. Nézzük meg ezt a következő példa segítségével:E példában a pék a példa arra, hogy ki pótolható, de ő példázza azt is, hogy kit nem lehet pótolni.
A későbbi azonosíthatóság miatt érdemes megjelölni a szavak helyét (sorrendjét a mondaton belül). Erre azért lesz szükség, hogy kezelni tudjuk a szavak többszöri előfordulásait is. Mivel a szótárba nem kerülnek be a központozási jelek, csak a szavak, így a fenti mondatot húsz szóalakra bonthatjuk fel:E(1) példában(2) a(3) pék(4) a(5) példa(6) arra(7), hogy(8) ki(9) pótolható(10), de(11) ő(12) példázza(13) azt(14) is(15), hogy(16) kit(17) nem(18) lehet(19) pótolni(20).
Ezt a húsz szót a lexikografikus elv alapján rendezve a szabály két összetevője közül két esetben alkalmazhatjuk az első komponenst. Az 'a' és a 'hogy' szavak esetében a formula első komponesét kell mindvégig alkalmazni, vagyis e két-két szóelőfordulásra a szabály azt hozza ki, hogy legalább olyan jók, mint a másik, hiszen a szavak minden pozíciójában megegyeznek a betűk. A többi esetben a lexikografikus szabály mindkét összetevőjét figyelembe kell venni, és mindig találhatunk egy olyan pozíciót az egyes szavakon belül, amelyekben az éppen összehasonlított szavak valamelyikének betűje megelőzi a másik szó betűjét. Az 'azt' és az 'arra' szavak esetében például a második pozícióban levő betűk esetében az 'r' előbb van a 'z' betűhöz képest az ábécé szerinti rendezés szerint, amiatt az 'arra' szavunkat előbbre soroljuk az 'azt' szavunkhoz képest. Az egybetűs szavakat már az első pozíció alapján rendezni lehet (ezért kerül előbbre az 'a' az 'e' vagy 'ő' szavakhoz képest), a több betűből álló szavaknál a későbbi pozíciók alapján lehet csak sorrendet kialakítani a szavak között. "Példaszótárunk" összeállításában a hatodik pozícióig el kellett menni ahhoz, minden szóról el tudjuk dönteni, hol a helye (a 'példában' és 'példázza', illetve a 'pótolni' és 'pótolható' szavak esetében).| \# | szó | (\#) | $pr_1$ | $pr_2$ | $pr_3$ | $pr_4$ | $pr_5$ | $pr_6$ | $pr_7$ | $pr_8$ | $pr_9$ | |||
| \multirow{2}{*}{1-2}&a&\begin{scriptsize}(3)\end{scriptsize} &a&&&&&&&\\ | ||||||||||||||
| a | (5) | a | ||||||||||||
| 3 | arra | (7) | a | r | r | a | ||||||||
| 4 | azt | (14) | a | z | t | |||||||||
| 5 | de | (11) | d | e | ||||||||||
| 6 | e | (1) | e | |||||||||||
| \multirow{2}{*}{7-8}&hogy&\begin{scriptsize}(8)\end{scriptsize} &h&o&g&y&&&&\\ | ||||||||||||||
| hogy | (16) | h | o | g | y | |||||||||
| 9 | is | (15) | i | s | ||||||||||
| 10 | ki | (9) | k | i | ||||||||||
| 11 | kit | (17) | k | i | ||||||||||
| 12 | lehet | (19) | l | e | h | e | t | |||||||
| 13 | nem | (18) | n | e | m | |||||||||
| 14 | ő | (12) | ő | |||||||||||
| 15 | pék | (4) | p | é | k | |||||||||
| 16 | példa | (6) | p | é | l | d | a | |||||||
| 17 | példában | (2) | p | é | l | d | á | b | a | n | ||||
| 18 | példázza | (13) | p | é | l | d | á | z | z | a | ||||
| 19 | pótolható | (10) | p | ó | t | o | l | h | a | t | ó | |||
| 20 | pótolni | (20) | p | ó | t | o | l | n | i | |||||
| arkhimédeszi rendezés | 1, 2, 3, 10, 11, 12, 13, 20, 21, 22, 100, 101 | |||||||||||||
| lexikografikus rendezés | 1, 10, 100, 101, 11, 12, 13, 2, 20, 21, 22, 3 | |||||||||||||
$x/y \equiv\concept{BUT}(x,y) \defi (x\cap y)\cup y^{<}$
de (operátor) (hun) – but (operator) (eng)
$x\| y \equiv\concept{ON\_THE\_OTHER\_HAND}(x,y) \defi x\cap y$
másfelől (operátor) (hun) – on the other hand (operator) (eng)
Az operátorok jelentésének értelmezéséhez segítséget jelenthet, ha arra gondolunk, hogy miként vesszük figyelembe a hierarchiába szervezett emberek véleményét. Amikor emberek egyetértenek, akkor bárhol is legyenek a szervezeten belül, a "közös véleményük" is az lesz, amit egyenként helyeselnek. A kérdés az, hogy miként összesítsük az eltérő véleményeket. Ezen a ponton lehet megérteni a két operátor szemantikáját. Amikor alá-fölérendeltségi viszonyban levő emberek véleménye eltér, akkor a magasabb ponton levő (a szervezeten belül nagyobb prioritással rendelkező) ember véleményét vesszük figyelembe. Ha i és j a két személy, és i van az alárendelt szerepben j-hez képest ($i<{j}$), akkor azt mondjuk, hogy "i véleménye az, hogy x, de j azt gondolja, hogy y", és ez utóbbi számít. Alá-fölérendeltségi viszony esetén tehát a de (but) operátort alkalmazzuk. Amikor viszont két ember azonos hierarchikus szinten van, akkor az eltérő véleményeik között nem tételezünk prioritási különbséget, azonos mértékben vesszük figyelembe őket. Ekkor azt mondjuk, hogy "(egyfelől) i azt gondolja, hogy x, másfelől j úgy véli, hogy y". Ilyen esetekben a másfelől (on_the_other_hand) operátort használjuk. Érdemes még megjegyezni, hogy bár matematikai értelemben elégséges a fenti két operátort definiálni, létezik egy harmadik is, amit leginkább akkor lehet értelmesen igénybe venni, amikor az elmélet alkalmazni akarjuk a társadalmi cselekvések leírásakor. A but operátorban ugyanis megcserélhetjük az argumentumok változóit. Ez a reláció (operátor) konverzének felel meg, amit logikailag kifejezhetünk új kategória felvétele nélkül is. Azért érdemes mégis említeni (és felvenni a modellbe) ezt a "másik irányú" relációt (operátort), mert közel sem mindegy, hogy melyik végén áll az ember egy alá-fölérendeltségi viszonyban. Az új operátor definíciója, amelyhez – a de operátorhoz képest megfordított jelentésének jelzésére – az ed (tub) nevet rendelném hozzá, a következő.$y/x \defi (y\cap x)\cup x^{<}\equiv x/^{- 1}y$
ed (operátor) (hun) – tub (operator) (eng)
Mivel az új operátor matematikai értelemben redundáns, az elmélet további kifejtésekor nem számolunk vele, noha később még hivatkozhatunk rá. A két alapoperátor viszont két ok miatt is nagyon fontos. Egyrészt bizonyítható, hogy bizonyos feltételeknek [♦] megfelelő, végesrendű operátor meghatározható a két alapoperátor és a változók segítségével ( [HAndr] ), másrészt a két operátorra támaszkodva definiálhatunk egy preferenciális algebrát is, ami az elméletet nagyon erőssé teszi. Ehhez az alábbi axiómákat kell rögzítenünk.
$x \| x = x$
$x \| (y \| z) = (x \| y) \| z$
$x \| y = y \| x$
$(x/x) = x$
$x/(y/z) = (x/y)/z$
$(x \| y)/z = (x/z) \| (y/z)$
$(x/y)\| x = x \| y$
preferenciális algebra (hun) – preferential algebra (eng)
A fenti tételek a két operátor idempotens, illetve asszociatív jellegét, a but művelet kommutativitását, a but művelet disztributivitását az on_the_other_hand operátorra nézve, valamint utóbbi művelet egy abszorbtív jellegű tulajdonságát mondják ki (☜) Ez az algebra azért is különösen fontos, mert ez a modellt értelmezhetjük a hierarchia jelenségének leírásaként is. Márpedig a hierarchia fontosságát nem kell különösebben ecsetelni. A biológiában, kognitív tudományban a hierarchia két fontos típusaként a beágyazott és nem-beágyazott hierarchia típusait elkülönítve egymástól fontos tételként kezelik azt, hogy az élő rendszerek (így az emberi agy is) beágyazott hierarchiaként jellemezhetőek [ToddE] A szervezetszociológia a munkaszervezés világának vagy még általánosabban a szervezetek szervezésének egyik kiemelten fontos módjaként elemzi a hierarchiát [Steph] Az általában vett szervezés, irányítás területén a hierarchia elvének előnyeiről szól Herbert Simon híres órás példája [Herbe] A mérnökök az általuk tervezett rendszerek irányításának eltérő logikáját próbálják megragadni a hierarchikus és heterarchikus irányítás kettősségével [Vamos] Az archívumok, könyvtárak világában a tartalmi eligazodást segíteni hivatott tudásszervezési rendszerek szervezési módjai között elkülönítenek egymástól kétféle hierarchiafogalmat, a monohierarchia, illetve a polihierarchia típusait [syi:e] [♦] Nagy lépést tettek meg Andrékáék, amikor egyetlen modellbe vonták össze a személyen belül, illetve személyek között egymás mellett létező, versengő preferenciarelációk leírását mondván, hogy formális szempontból a személyen belüli preferenciakonfliktusok azonos lényegűek a személyek közti preferenciaütközésekkel. Ez azt is jelenti egyben, hogy a mindkét önállóan kutatott szakterületnek lehet mondanivalója a másik számára, azaz a társadalmi választások elméletének relevanciája lehet az egyéni preferenciakezelést leíró elmélek számára, és fordítva. Persze arra azért vigyázni kell, hogy ne kövessünk el túláltalánosításokat. Mindenesetre nagyon izgalmasak azok az új kísérletek, amelyek ezen a nyomvonalon haladva próbálják meg minél pontosabban leírni a preferenciák kezelésével, dinamikájával, változásaival kapcsolatos jelenségeket [deJon] [Fenro] [Girar](A)racionális (a)racionális
Akármelyik értelmezését is fogadjuk el a racionalitás fogalmának, ha elkötelezzük magunkat valamelyik definíció mellett, és ennek szellemében vizsgálni kezdjük az emberek viselkedését, akkor biztosak lehetünk benne, hogy a tényleges társadalmi gyakorlatban rengetegszer megsértik a racionalitás elvét. Ennek sok oka van. Szemléltetésként vegyük a többszempontú döntési helyzetek példáját. Amikor valaki egyetlen szempont szerint akar választani az alternatívák halmazából, akkor ezt megteheti a szemponthoz "illeszkedő" preferenciareláció segítségével. Amikor azonban több szempont is felmerül a választás során, akkor a választás döntési helyzetté alakul, ami annyiban lesz több és más, hogy az eltérő szempontok más és más rendezéseket eredményezhetnek. Ezt nyilván kezelni kell valahogy, amit azonban többféleképpen tehetünk meg. A döntéselmélet – legalább részben – ennek a problémának a tárgyalására jött létre. A sokféle szempont egyeztetése során lehetséges, hogy a szempontokat egyenrangúaknak, nem rendezetteknek tekintik, és lehetséges, hogy különböző szintekre sorolják, vagyis rendezik őket. Nem célom itt az egyéni döntési eljárások, módszerek, szabályok ismertetése. [♦] A probléma érzékeltetése végett röviden bemutatok három jól ismert, sokat elemzett döntési stratégiát, a maximin, a maximax és a minimax szabályt. A maximin szabály, amit neveznek még pesszimista, biztonságra törekvő, kockázatkerülő módszernek, Wald-féle Wald kritériumnak, a legrosszabbak legjobbikát választja ki az alternatívák közül. A szabály lényege, hogy első körben kiválasztja az alternatívák egyes szempontok szerinti leggyengébb értékelését, majd második körben ezen leggyengébb elemek közül kiválasztja a legjobbat. A maximax szabály vagy másként az optimista módszer első körben kiválasztja az alternatívák egyes szempontok szerinti legerősebb értékelését, majd második körben ezek közül veszi a legjobbat. Ez módszer tehát a legjobbak legjobbikát keresi meg. A minimax szabály megkeresi az egyes szempontok szerint várható legrosszabb eredményeket, és ezek közül kiválasztja a legkisebb veszteséget ígérő alternatívát. Ez a szabály kockázatsemleges, az elmaradó haszon minimalizálására törekszik, arra, hogy a döntéshozónak a végén a legkisebb legyen a megbánása. A módszert nevezik még Savage vagy Savage-Niehans-kritériumnak is. A maximin és a maximax szabályok közti különbség szemléltetésére megidézem itt Carl Hempel példáját [HEMPE]
A maximin szabály szerint első lépésben megkeressük a két doboz minimumát, ami az ólom (1) és az ezüst (10), második lépésben pedig vesszük a minimumok közül a legnagyobbat, ami az ezüst. A maximax szabály először megkeresi a két doboz maximumát, ami itt a platina (1000) és az arany (100), majd másodjára kiválasztja utóbbiak maximumát, vagyis a platinát. Láthatjuk tehát, hogy két – egyaránt elfogadhatónak és racionálisnak tűnő – módszertan alapján más eredményekhez jutunk. Ez mindenképpen magyarázatra szorul. Amikor értelmezni akarjuk a stratégiákat, megakarjuk magyarázni a különbségeket, akkor már nem segítenek minket az eddig bemutatott racionalitásdefiníciók. Itt már más tényező(ke)t kell beemelnünk a magyarázó modellbe. Úgy tudunk magyarázatot adni, ha hivatkozunk a döntést hozó személyek személyiségjegyeire, temperamentumára, beállítódásaira, hangulataira. Ezek ismerős fogalmak – az érzelmi, affektív jelenségek világából (☜) A racionális elvek helyett (vagy mellett) az érzelmi heurisztikákra, érzelmi-tapasztalati mechanizmusokra támaszkodó cselekvések elemzése a viselkedés-gazdaságtan területére tartozik. A viselkedés-gazdaságtan a magatartástudományok és a gazdaságtan metszetében helyezkedik el. Bár alapvetően gyakorlati irányultságú, vagyis az emberek tényleges viselkedését megfigyeléseken és kísérleteken keresztül próbálja meg leírni és értelmezni, azért két fontos előzményét vagy inkább elméleti alapját érdemes említenem. Az egyik az Amos Tversky és Daniel Kahneman munkássága alapján kibontakozó kilátáselmélet (prospect theory), a másik a Herbert Simon nevéhez köthető korlátozott racionalitás (bounded rationality) elmélete. Az új megközelítések közös vonása az a felismerés, hogy kockázatos vagy bizonytalan döntési helyzetekben, amikor úgy kell döntenünk, hogy nem áll rendelkezésre minden információ, akkor eltérünk a racionalitáselméletek által elvárt elvektől, megoldásoktól. A kilátáselmélet arra fókuszál, hogy milyen hüvelykujjszabályok, döntési heurisztikák alapján hozzuk meg tényegesen a döntéseinket, a korlátozott racionalitás elmélete pedig azt hangsúlyozza, hogy a tökéletes döntések helyett legtöbbször megelégszünk az elégséges, még elfogadható döntésekkel, vagyis korlátozott racionalitás vezérel minket. Herbert Simon a korlátozott racionalitásról szóló tézisében arra hivatkozik, hogy az ember saját korlátozott információfeldolgozó képessége miatt nem tud teljesen racionális lenni [SIMON] [proce] [Herbe] A racionális döntéshez minden szempontot össze kellene gyűjteni, minden lehetséges kimenetet, minden célt, a hozzájuk tartozó eszközökkel, azok következményeivel, mellékhatásaival együtt figyelembe kellene venni. Ezzel szemben sosem áll rendelkezésünkre az elvileg szükséges információ. Ha viszont elképzelnénk azt az esetet, hogy valamiért, valahogyan mégiscsak szert tennénk minden információra, azt a hatalmas mennyiségű és bonyolultságú információhalmazt nem lennénk képesek feldolgozni. Gyakorlatilag mindig beszerzési és feldolgozási gondjaink adód(ná)nak.
"Egy olyan világban, amelyben viszonylag szűkösek az információk, és amelyben csupán néhány, egyszerű döntési problémát kell megoldani, az információ majdnem mindig pozitív jószágnak számít. Egy olyan világban, amelyben a figyelem az egyik legszűkösebb erőforrás, az információ költséges luxuscikk is lehet, mivel figyelmünket a fontos dolgokról kevésbé fontosakra terelheti." [proce]
Az ilyen helyzetben az embernek az lehet az egyetlen értelmes válasza, hogy "feladja" az teljes racionalitás iránti elvárását, pontosabban az ilyen helyzetben a cselekvést elemző, értelmező kutatónak kell feladnia az ember teljes racionalitására vonatkozó hipotézisét. Simon is ezt lépte meg, amikor bevezette a korlátozott racionalitás tézisét, ami szerint a hétköznapi gyakorlatok során megelégszünk a (még éppen) elfogadható döntésekkel, nem törekszünk teljességre. A racionalitás legnagyobb "ellensége" tehát sajátmaga, pontosabban a racionalitás illúziója, vagyis annak fel nem ismerése, hogy az ember (a döntéshozó) szükségszerűen korlátos kognitív képeségekkel rendelkezik. Ennek számtalan jele, bizonyítéka van, ami leginkább abban nyilvánul meg, hogy az előttünk álló lehetőségekre vonatkozóan mindig kockázatokkal, bizonytalanságokkal kell számolnunk, és ezek kezelésében nagyon sokszor gyengék vagyunk, tévedünk, hibázunk, félremagyarázunk [mero:] Balhiteink egyik látványos példája a véletlen jelenségének félreértelmezése, amire a "szerencsejátékos tévedéseként" szoktak hivatkozni. A hétköznapi ember számára nem evidens, hogy minden lottóhúzás alkalmával ugyanannyi esélye van valamennyi számkombinációnaknak a nyerésre (például az 1-2-3-4-5 sornak). Ezt a tény, hogy ti. a véletlenen alapuló rendszereknek nincs emlékezete, az emlékezettel rendelkező emberek nagy része nem tudja megfelelően kezelni [mero:] Amos Tversky és Daniel Kahneman kilátáselmélete, sőt a viselkedés-gazdaságtan egésze felfogható egy olyan heurisztikagyűjteményként is, amelynek segítségével értelmezhetjük, hogy mikor, milyen módokon és miért döntünk a tényleges társadalmi gyakorlatban. [♦] A kilátáselmélet egy legismertebb fogalma a keretezési hatás (framing effect) jelenségét írja le. A keretezés lényege, hogy kockázatos helyzetekben az emberek attól függően (is) döntenek, hogy milyen módon, pozitív vagy negatív formában tálalják a döntési lehetőségekre vonatkozó információt [Kahne] Tverskyék híres kísérletében a következő lehetőségekből kellett választani. Ha egy 600 ember életét veszélyeztető járvány leküzdésére két programot dolgoznak ki, és (i) az első program szerint 200 ember életét lehet biztosan megmenteni, míg (ii) a második programban egyharmadnyi eséllyel megmenthetik mind a 600 embert, de kétharmadnyi valószínűséggel mindenki meghal, akkor a kísérleti alanyok 72%-a az első opciót választotta – miközben a két opció a várható hasznosságok szempontjából megegyezik. Ha viszont úgy tették fel a kérdéseket, hogy (iii) a harmadik program alapján 400 ember biztos meghal, viszont (iv) a negyedikben egyharmad valószínűséggel senki sem hal meg, míg kétharmadnyi esélye van annak, hogy mindenki meghal, akkor megfordult a szavazatarány, és a negyedik alternatívát választották 78%-nyian. A keretezésnek tehát iszonyú ereje tud lenni. A reklám, a marketing igen jelentős részben erre a jelenségre épül rá. Tverskyék másik "újítása" a tükrözési hatás (reflection effect) fogalmának bevezetése volt, amivel azt írták le, hogy az emberek döntő többsége kockázatvállalóként viselkedik, ha rizikós döntésében lehetséges veszteségekkel szembesül, de kockázatkerülővé válik, amikor lehetséges nyereségek között választ [kahne] A tükrözési hatás fogalmával azt a jelenséget írhatjuk le, hogy ha a kísérleti alanyokat pozitív, illetve negatív keretbe helyezzük, akkor választásaik egymás tükörképei lesznek. Az előző járványos példasorban a pozitív keretben előadott bizonytalanabb (ii) alternatívát jóval kevesebben választották, tehát kockázatkerülők voltak, míg a negatív előadásmód prezentálásakor kockázatvállalóak lettek, miközben a bizonytalanabb (iv) opcióra szavaztak inkább. Ezt jelenti az, hogy a két választás egymás tükérképe. A bizonyossági hatás (certainty effect) fogalma azt a jelenséget írja le, amikor az emberek túlértékelik a biztos kimeneteket a bizonytalanokkal szemben. Eszerint amennyiben valaki választhat a teljesen biztos 80 forint vagy a 80%-os bizonyosságú 100 forint között, akkor az előbbit választják (noha a két kimenet várható hasznossága teljesen egyforma). E hatás következtében egyébként várható nyeremények esetében a kockázatkerülő beállítódás válik dominánssá. Tversky és Kahneman elmélete természetesen követőkre talált, akik további anomáliák, irracionalitások létezésére mutattak rá. A felidézési előítélet (availability bias) szerint az ember nem is annyira aszerint tudja előhívni az információt a memóriájából, hogy az milyen gyakran vagy ritkán történik meg, tehát nem az ismertség, megszokottság kontra ismeretlenség, szokatlanság a felidézési képesség és gyorsaság fő meghatározója, hanem inkább az eseményekhez kapcsolt szubjektív fontosság. Könnyebben felidézzük az érzelmi töltéssel elraktározott eseményeket, kimeneteket. Ezért értékeljük felül a gyilkosságokat, a súlyosabb bűncselekményeket. A birtoklási hatás (endowment effect) szerint a már birtokolt tárgyak iránti elkötelezettségünk indokolatlanul magasabb. Az emberek azokat a javakat, amelyek már birtokában vannak, sokkal magasabbra értékelik, mint amelyeket még csak meg kellene szerezniük. Dan Ariely és munkatársai végeztek kísérleteket a tulajdonlás érzelmi töltetének vizsgálatára [DanAr] Az egyik rangos egyetemen az éves kosaras szuperrangadóra az egyetemisták összlétszámához képest csak nagyon kevesek juthattak be, ezért sorsolással döntötték el az érdeklődők tömegéből ki juthat jegyhez a meccsre. A kutatók megtudakolták, mennyiért vennének jegyet azok, akik elestek a vásárlási lehetőségtől azoktól, akiknek lett jegyük, óriási különbség alakult ki a kereslet és kínálat között: a lemaradók legfeljebb 175 dollárt voltak hajlandók áldozni egy jegyre, míg legalább 2400 dollárt kértek volna érte a szerencsés jegytulajdonosok. "Érzelmi szakadék támadt azok között, akik lélekben már a mérkőzés nagyszerűségére készültek, és azok között, akik arra gondoltak, mi mást is vehetnének a jegy áráért." A magyarázat: a tulajdonlás átalakít bennünket, mert érzelmi kapcsolatot teremt a tulajdonunk és saját magunk között. Tulajdonosi tudat esetén már működni kezd a tulajdon elvesztésétől való félelem. Sőt, ez már a részleges tulajdonlás esetén is így van! Ezért hajszolják bele magukat olyan gyakran a magasabb árajánlatokba a licitáló felek az aukciók során, de – részben – ezért működnek a virtuális tulajdonlás reklámtechnikái (elképzeljük magunkat a reklámozott termékkel együtt és azonnal érzelmi viszonyba kerülünk vele) vagy az elköteleződést kialakító ingyenes kipróbálási időszakok. A birtoklási hatás mélyén elég nyilvánvalóan a status quóhoz való ragaszkodás húzódik meg. A status quótól való eltérést ugyanis az emberek mindenképpen kockázatosnak ítélik. A status quo előítélet (status quo bias) hasonló ehhez, csak ekkor nem az eredetileg birtokolt tárgyhoz, hanem az eredetileg kialakított döntéshez ragaszkodnak az emberek. Erre mindenki sok példát hozhatna saját életéből. A reprezentativitási előítélet (representativeness bias) az a potenciális irracionalitás bennünk, hogy nehezen tudjuk jól kezelni a statisztikai reprezentativitás fogalmát a gyakorlatban. Erre Hámori Balázs példáját idézem [hamor]"Tételezzük fel, hogy Péter halálmegvetően bátor ember. Mi a valószínűbb, hogy alpinista, vagy az, hogy könyvtáros? Tegyük fel továbbá, hogy az alpinisták 90 százaléka bátor, míg a könyvtárosoknak csak 5 százaléka. Az országban 100 alpinista található és 5400 könyvtáros, azaz ekkora a minták nagysága. Ebből az következik, hogy 90 bátor alpinistára 270 bátor könyvtáros jut. Háromszoros a valószínűsége tehát annak, hogy Péter könyvtáros, mint annak, hogy alpinista. Mégis 100 megkérdezett ember közül 99 az előbbi kérdésre azt feleli, hogy Péter alpinista, noha nyilvánvalóan tudatában van annak, hogy sokkal kisebb valószínűséggel hozza össze a sors egy alpinistával, mint egy könyvtárossal."
Amit Tverskyék a beakaszkodás és igazodás (anchoring and adjustment) kifejezéssel ragadtak meg, azt Ariely az etológiából ismert bevésődés (imprinting) fogalmával írta le. A bevésődés vagyis az első élmények meghatározó jelentősége megfigyelhető az emberi döntésekben is. Egy új termékkel, szolgáltatással kapcsolatban az első élmények alapján kialakítunk referenciapontokat, amelyektől aztán a későbbiekben sem nagyon vagy csak nehezen mozdulunk el. Sok esetben nem (csak) a kereslet-kínálat törvénye szabja meg a piaci árakat, hanem a bevésődés is hathat az árak alakulására. Egy érdekes kísérletben a kísérleti alanyoknak különböző termékek árát kell megbecsülniük, de mielőtt belekezdtek volna, le kellett írniuk a saját társadalombiztosítási számukat a papírra. Akiknek nagyobb száma volt, azok szisztematikusan magasabb árakat írtak be a megadott terméklistára, mint azok, akiknek kisebb volt a száma. Dan Ariely azt állítja, hogy a – hagyományos racionalitásfelfogás szerint – irracionálisnak minősíthető döntéseink sokszor nagyon is kiszámíthatóak [DanAr] A döntéseinkben sokszor felismerhető heurisztikák belső logikája néha nagyon könnyen megmagyarázható. [♦] Sokszor egyszerűen csak arról van szó, hogy a nehéz döntések helyett a könnyebbet választjuk, ami viszont befolyásolja, olykor meghatározza az alternatívákra vonatkozó tartalmi döntéseinket is. Ariely egyik példája az Economist előfizetési opcióival volt kapcsolatos. Először három lehetőséget kínáltak fel a leendő olvasók számára: (i) a nyomtatott változatot 85, (ii) az online hozzáférést 125, végül (iii) mindkettő lehetőséget egyszerre 125 dollárért. Ilyen feltételek mellett az előfizetők nagy arányban a kettős hozzáférési lehetőséget kérték. Amikor azonban – egy második kísérletben – a középső opció elmaradt, akkor sokkal inkább az első, csak a nyomtatott előfizetési lehetőséget választották. Ez azzal magyarázható – mondja Ariely –, hogy amikor nehezen összehasonítható alternatívákból kell választanunk, akkor öntudatlanul leszűkítjük a döntési mezőt azokra az opciókra, amelyeket egymással könnyebben összemérhetünk. A második kísérletben azon valóban gondolkodni kell, hogy a nyomtatott vagy az online változatot vegyük-e meg, vagyis az (i) és (iii) ajánlatok közti választásnak "tétje" van, a döntésbe "munkát kell befektetni". Amikor viszont az első kísérletben az a) mellett a (ii) és (iii) opciókat is össze lehet hasonlítani, akkor az utóbbi kettő közti döntés nagyon könnyű, és – akaratlanul is – ez a könnyűség határozza meg magát a döntés tartalmát. A második kísérlet tanúsága szerint abban az értelemben irracionális ez a döntés, hogy a többség – ha már egyszer hajlandó vagy épp rá van kényszerítve az alapos mérlegelésre, akkor – mégis inkább az első ajánlatot kéri, míg a "lustaságot megengedő" döntési helyzetben az ezzel ellentétes opciót választja. A példa szerint tehát irracionálisak vagyunk, de – teszi hozzá Ariely – ez az irracionalitás kiszámítható, hiszen meg tudjuk magyarázni, előre tudjuk jelezni. Hasonló eredményeket hoztak az olyan kísérletek, amelyekben Párizsba, illetve Rómába szóló, ingyen reggelivel összekötött hétvégi utazási ajánlat mellé betettek egy másik római utat ingyen reggeli nélkül. A döntő többség a csali ajánlattal támogatott római utat választotta (a "Róma vagy Párizs" nehéz döntés helyett a "Róma reggelivel vagy Róma reggeli nélkül" könnyű döntést választották, ami után már nem volt kérdés, hogy a "Róma reggelivel" opció jobb a reggeli nélküli változatnál). Egy másik kísérletből kiderült, hogy két ember arcképe közül is azt látjuk szimpatikusabbnak, amelyik mellé beteszik annak eltorzított, csúnyább változatát is. De ugyanezen viszonylagossági tényező miatt viselkedünk másként akkor, amikor hajlandók vagyunk egy utcasarokkal távolabb menni, hogy megvegyünk 18 dollárért egy tollat, ha tudjuk, hogy 7 dollár kedvezményt adnak a 25-ből, míg nem tesszük meg ugyanezt akkor, ha megtudjuk, hogy azt a 455 dolláros öltönyt, amelyet valahol már kinéztünk, megkaphatnánk kicsit távolabb 7 dollárral kevesebbért. Jellemző ránk az ingyenességhez való viszonyunk is. Egy kísérletben két csokifajtát, egy nagyon magas és egy közepes minőségű csokit árusítottak a járókelőknek. A különleges csoki árát levitték 30 centről 15-re, az átlagos csokit viszont nagyjából a megszokott áron, 1 centért kínálták. Ilyen feltételek mellett a vásárlók háromnegyede a drága, egynegyede az olcsó csokit választotta (a 14 centes árkülönbség ellenére a jelentős árengedmény nagy csáberőt jelentett). Amikor azonban további 1-1 centtel csökkentették mindkét termék árát, a vásárlási hajlandóság teljesen eltolódott az olcsóbb, akkor már ingyenes csoki irányába. Az ingyenesség hatását sokféle módon vizsgálták, és mindig ugyanazt tapasztalták: az ingyenesség mágnesként vonzza az embert. Egy másik egyszerű kísérletben egy bevásárlóközpont bejáratánál 7 dollárért osztogattak egy 20 dolláros ajándékutalványt, illetve ingyen egy 10 dollárosat a vásárlóknak. Annak ellenére, hogy anyagilag jobban jártak azok, akik fizettek a 20 dolláros utalványért (ők 13 dollárt nyertek az ügyleten), az elsöprő többség a 10 dolláros ajánlatot fogadta el, ahol nem kellett semmit sem fizetnie. Az ingyenesség varázserejét Ariely úgy magyarázza, hogy amikor a döntéseink során mérlegeljük a lehetséges előnyöket és hátrányokat, sokkal jobban félünk a rossz döntéseink nyomán esetleg bekövetkező veszteségektől, mint amennyire vonzanak a várható előnyök. Ha pedig valamit ingyen szerezhetünk meg, ez olyan érzelmi többletet ad az ingyenes alternatívának, ami legyőzi az előzetesen kalkulált veszteségérzetet. Jól ismert az előzetes várakozások döntésbefolyásoló szerepe is: jobban ízlik ugyanaz a sör, ha úgy tudjuk, márkás gyártótól származik, jobban tetszik a mozifilm, ha nagyon jó előzetes kritikát kapott, egy szépen megterített asztalnál ülve finomabbnak ítéljük meg az elfogyasztott vacsorát stb. Az előzetes elvárások (vagy mondjuk így: sztereotípiák) gyakran előkészítik mind a cselekvőket, mind a véleményt formálókat, így azután az előzetesen várt eredmény be is következik (tehát az előítéletek sokszor önbeteljesítő próféciaként működnek). Hasonló a placebohatás esete: a placebo tényleg működik, a drágább gyógyszereket hatásosabbnak érezzük. Az előítélet, sztereotípia viszont hasznos is tud lenni, mert nem lehet mindig, mindent a nulláról indítva megítélni, dönteni. Paul Slovic az "arány dominanciája" kifejezéssel illetve idézte fel C.K. Hsee kísérleti példáját amelyben ha a kísérleti alanyoknak fagyit kínáltak nagy pohárban, de nem teletöltve vagy kis pohárban, de jól megpúpozva, akkor a legtöbb kísérleti alany az utóbbit választotta. Ez az arány megfordult, ha a két poharat egymás mellé tették, és összemérhetővé vált a két pohár nagysága [PaulS] Ezekről a heurisztikákról már volt szó korábban. Akkor, amikor az indulati-érzelmi cselekvések jellemzésekor bemutattam Zajonc, Epstein, Bruner, Slovic elméleteiben található megkülönböztetést a racionális-analiktikai és a tapasztalati-érzelmi gondolkodásra és megismerésre vonatkozóan (☜) A viselkedés-gazdaságtan legfontosabb üzenete az, hogy nem minden helyzetben racionális az ember, és amikor nem az, akkor különféle heurisztikák szerint cselekszik. A kétféle viselkedés kétféle gondolkodást, kétféle beállítódást feltételez, és az a nagy kérdés, hogy meg tudjuk-e mondani, mikor melyik válik dominánssá. Hámori Balázs ezt a termelési logikák, amunkavégzés minőségének átalakulásával véli magyarázhatónak."Addig talán rendben is volt a racionalitás axiómaként, modellen kívüli, a priori adottságként kezelése, amíg a gondolkodás, az értelem működése, az információk feldolgozása csak másodlagos kísérőjelenség volt az alapvetően materiális természetű gazdasági folyamatokban. Ma azonban, amikor egyre több ember számára a gondolkodás, a döntés nem a termelést megszakító epizód, hanem maga a munka, már nem kielégítő minden további vizsgálódás nélkül elfogadni az emberi gondolkodásra vonatkozó feltételezéseket." [hamor]
Bizonyos mértékig helytállónak gondolom ezt az érvet, de azt hiszem, hogy ennél többről és részben másról van szó. Szerintem különböző helyzetek az ember másfajta képességeit aktivizálja és így másfajta cselekvésre készteti. Ebben a döntő külünbséget az a kétféle megismerési, gondolkodás szisztéma közli választás vagy inkább választódás jelenti. Bizonyos helyzetekben az érzelmi-tapasztalati séma, máskor meg a racionális-analitikai séma mentén működünk. Lehet, hogy tendenciaszerűen korszakolni lehet az emberiség történelmét, hogy milyen helyzeteket állít elő, és ebből fakadóan milyen működési logikák aktiválódnak bennünk. Egy erre tett javaslatként fogom fel Hámori fenti gondolatát. De a jelenség jobb megértéséhez még szükségünk van arra, hogy a helyzettípusok és az aktiválódó magatartási sémák közti kapcsolatot jobban le tudjuk írni.Összefoglalás
A weberi cselekvéstípusok elemzése után szükségesnek tartok néhány észrevételt tenni. Azt, hogy miért a racionalitás fogalma van a tipológia középpontjában, hogy a racionalitás fogalma mentén "sorba lehet " fűzni a négy weberi cselekvéstípust, sokan megírták már, még maga Weber is [szant] Bertalan László figyelmeztett rá, hogy a weberi racionalitásfogalomnak van egy szűkebb és egy tágabb értelmezése [berta] A szűkebb értelmezés szerint racionálisnak csak a célracionálist tarthatjuk, és a további három típus, tehát az értékracionális, az érzelmi és a habituális valamilyen mértékig irracionális. A tágabb értelmezés szerint racionális a célracionális és az értékracionális, míg irracionális az érzelmi és a habituális. Ezt Weber is pont így látta."A cselekvés » racionalizálásának« egyik lényeges eleme, hogy a meggyökeresedett szokáserkölcshöz való belső alkalmazkodást az érdekviszonyokhoz való tervszerű alkalmazkodás váltja fel. De ez persze nem meríti ki a cselekvés » racionalizálásának« fogalmát. Ezen kívül beszélhetünk még értékracionalizálásról, ha tudatos értékek kerülnek a szokáserkölcs, és nemcsak a szokáserkölcs, hanem az indulati-értelmi cselekvés helyére. Végül lejátszódhat a racionalizálás úgy is, hogy az értékekbe vetett hittől mentes, tisztán célracionális cselekvés kerül az értékracionális cselekvés helyére." [weber]
Abban viszont már koránt sincs ilyen egyetértés, hogy az érdek, az érdekvezérelt cselekvés fogalmának vajon milyen a viszonya a weberi négyes cselekvésfelosztáshoz. Elég széles körben népszerű az a nézet, hogy egyfelől az érdekvezérelt cselekvés megegyezik a célracionális cselekvés fogalmával, másfelől az érdek kategóriája az önzés fogalmával. Az első állítást akár még el is tudnám fogadni, de hogy mégsem teszem azt, annak az az oka, hogy a második azonosságot teljesen elfogadhatatlannak tartom, és a célracionális vagy érdekvezérelt cselekvést semmi esetre sem tartanám kizárólag egoista motívumokon alapuló cselekvésnek. Mégha sokan is gondolják ezt így. Albert O. Hirschman például az érdekek és a szenvedélyek viszonyáról, az érdek fogalmának megjelenéséről és elterjedéséről szóló kitűnő könyvében azt a kitételt használta, hogy az "érdek mint ésszerű, szándékos önzés" [Alber] és könyvében végső soron "azonosult" az alábbi idézetben foglalt véleményekkel."Sokan úgy vélték, hogy az érdek egyesíti a két kategória jobbik természetét, hiszen az értelem felértékeli és kordában tartja az önzés szenvedélyét, s ez a szenvedély irányt és erőt ad az értelemnek. Az ilyen módon elegyített emberi cselekvés, úgy tartották, mentes a szenvedélyek romboló hatásától és az értelem tehetetlenségétől." [Alber]
A következő fejezetben alaposabban elemzem majd a társas motivációk körét, akkor szó lesz az agoizmus, altruizmus viszonyáról, helyéről a társas motivációk egészén belül (☜) ezért itt csak azt erősítem meg újra, hogy a Weber által bevezetett célracionális cselekvés vagy a sokak által használt érdekvezérelt cselekvés fogalma nem kapcsolható kizárólagos módon össze az egoista motiváción alapuló cselekvés fogalmával. A célracionális cselekvéssel kapcsolatos további fontos észrevételem még, hogy bár a célracionális cselekvés a weberi tipológia középpontjában helyezkedik el, mert ez a fogalom kézenfekvő viszonyítási alapot ad a többi elemzéséhez is, de a fogalmi elemzés szempontjából vett központi szerep nem jár együtt szükségszerűen a valós társadalmi gyakorlatban való központi szereppel, elterjedtséggel. A racionalitás fontos az életünkben, fontos a társadalmak fejlődésében is, de a racionalitás sosem volt, most sincs és sosem lesz egyeduralkodó. A racionalitás kizárólagosságának, de talán még a racionalitás dominanciájának az elképzelése csak egy hamis mítosz. Ennek több oka is van."A racionalitás elve két teljesen eltérő módon sérülhet. Egyrészt az emberek minden igyekezetük dacára gyakran követnek el logikai következtetési hibákat. Másrészt a cselekvéseik sokszor 'meggondolatlanok': amikor a szokás vagy a szenvedély vezérli őket, akkor még csak nem is törekednek a racionális önkontrollra. (… a racionalitás effajta hibái, csakúgy, mint az önérdekvezéreltség posztulátumának megsértései, funkcionálisan adaptívnak bizonyulhattak az emberi faj genetikai és kulturális fejlődésében.)" [JackH]
Az előző részekben írtam sokat az aracionalitás gazdaságosságáról, racionalitásáról, a döntési paradoxonokról a döntéselmélet területéről, a korlátozott racionalitásról, a kilátáselmélet által megmagyarázható irracionálisnak ítélt jelenségekről, az érzelmeink, szokásaink ésszerűségeiről. Cselekvéseinket, magunkat csak úgy értjük meg, ha nem engedjük meg a leegyszerűsítő megközelítéseket. Az összefogalás végén bemutatok egy kicsit talán meglepő ábrát, ami a weberi cselekvéstípusok és néhány további fogalom viszonyát ábrázolja. Mondhatnám azt is, hogy az áttekintő ábrán a különböző motivációjú cselekvéstípusok egymáshoz való viszonyát a logika hatszög segítségével mutatom be, de ez csak formai értelemben igaz, tartalmilag nem. Hat (pontosabban: nyolc) Weber által használt fogalmat ugyanis be lehet mutatni egy olyan rendezésben, amely formailag megegyezik a logikai hatszög struktúrájával. A logikai négyszög sarokpontjaiba lehet betenni a négy weberi cselekvéstípus kategóriáját. A köztük levő viszonyt azon az alapon lehet megmagyarázni, hogy mindegyik cselekvéstípust az alapján ítéljük meg, hogy mennyi benne a tudatos mérlegelés. Az $\rel{(A)}$-sarokban levő célracionális cselekvés mindent mérlegel, ebben az értelemben univerzális kategória. A másik univerzális kategória az $\rel{(E)}$-sarokba tett habituális cselekvés, amikor is nincs semmi tudatosan mérlegelve. A két partikuláris kategória az $\rel{(I)}$-ben levő értékracionális cselekvés, illetve az $\rel{(O)}$-ban levő indulati-érzelmi cselekvés, amikor vagy egy szempont nincs (mert nem lehet) mérlegelve, vagy egyetlen szempont jelenik csak meg a tudatban, tehát csak azt lehet "mérlegeni". A négy cselekvéstípus mellett a szokáshoz igazodó cselekvést, illetve az e fogalom alá sorolt szokáserkölcs és érdekhez igazodó szokás, valamint a rendhez igazodó cselekvés fogalmát kell figyelembe vennünk. Ez nyolc kategória, de ezek közül a szokáserkölcs fogalma megfeleltethető a habituális cselekvés, az érdekhez igazodó szokás pedig a célracionális cselekvés fogalmának. A szokás fogalmának két altípusát maga Weber definiálta így, és ő volt az is, aki az érdek fogalmát a szokás kategóriája alá rendelte. Azt, hogy a két-két fogalom megfeleltethető egymásnak, azt én állítom [SyiWe] de úgy vélem, hogy ez a weberi definíciók alapján könnyen belátható. Ha viszont ezt elfogadjuk, akkor a logikai hatszög $\rel{(U)}$-pontjába behelyettesíthetjük a szokásvezérelt cselekvés kategóriáját úgy, hogy közben még az az összefüggés is fennmarad, miszerint a szokás és a célracionális (érdekvezérelt) és habituális cselekvés diszjunkciójaként írható le (☜) Azt is könnyen védhető javaslatnak érzem, hogy a normához igazodó cselekvés kifejezését felcserélhetjük a normavezérelt cselekvés teminusával. Weber ugyan másként tipizálta a rendhez igazodó (normatív) cselekvéseket, itt mégis megfontolhatónak érzem, hogy ezt a kategóriát betegyük a logikai hatszög $\rel{(Y)}$-sarokjába. A normához igazodásban ugyanis mindig van egy kicsi értékracionalitás és mindig van egy kicsi érzelem. Az értékracionális cselekvés furcsa keveréke az elköteleződésnek és a mérlegelő beállítódásnak – ez talán könnyebben elfogadhatónak látszik. Annak támogatására, hogy a normakövetésben ott lappang mindig az érzelem, Jon Elstert hívom segítségül, aki a következőket írta." … a szégyen(érzet) nem pusztán egyik támogatója a társadalmi normáknak, hanem a támogatója." [JonEl]
Megkockáztatom tehát, hogy a normavezérelt cselekvéshez szükséges mind az értékracionális, mind az indulati-érzelmi cselekvés együttes minősége (ahogy ezt a logikai hatszög $\rel{(Y)}$-pontjától "el lehet várni"). A hat cselekvéselméleti típuskategóriát tehát összefűzhetjük egymással a logikai hatszög sémája szerint, de azt nem állítom, hogy ezzel együtt a logikai hatszög esetén fennálló logikai kapcsolatokat is tételezhetjük köztük, sőt, ezek létezését tagadom. A hatszög szerkezete tehát csak bizonyos mértékig és bizonyos szempontból érvényes itt, de ha másra nem, legalább szemléltetési célokra alkalmas ez a párhuzam. Az ábrába felvettem még két új kategóriát, amelyek a mérlegelés minősége mentén fognak egybe két-két kategóriát. Az $\rel{(R)}$-pontba tett, mérlegelésen alapuló cselekvések alá tartozik a két racionális cselekvéstípus, míg a $\rel{(U)}$-sarokban levő nem mérlegelő kategória két altípusa a habituális és az indulati-érzelmi cselekvés. [♦]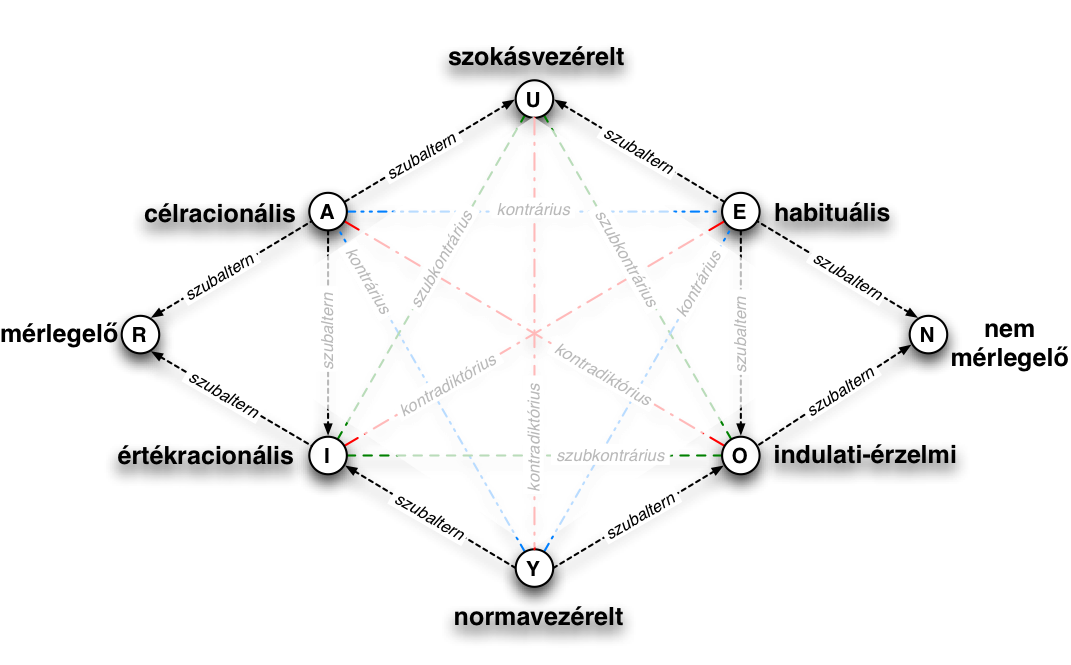
Társadalmi kapcsolat
"Sir Dannis Robertson [szerint] a közgazdász feladata megmutatni, hogyan lehet minimalizálni a legszűkösebb erőforrás, a szeretet iránti igényt. Azt követelte közgazdásztársaitól, hogy azonnal kezdjenek figyelmeztető csaholásba, ha olyan javaslatokkal találkoznak, melyek hatékony megvalósításához szeretetre van szükség." [James] "Egy racionális ágenstől általában elfogadjuk, ha saját érdekei szerint cselekszik. Egy mesterséges ágenstől azonban azt várjuk el, hogy valaki más (a felhasználó vagy a tervező) érdekében járjon el, aki az elvárásait valahogy közvetítette az ágens felé." [Towar]
A társadalmi cselekvés fogalmának elemzésekor kiderült, hogy a cselekvés fogalma annyiban szűkebb terjedelmű az egyszerű cselekvés fogalmához képest, hogy itt "megköveteljük" azt is, hogy a cselekvőn túl legyen még valaki, akihez a cselekvő – valamilyen módon – igazodik a cselekvésével (☜) Ekkor azonban ez a másik személy még csak közvetítő szerepet játszik: a társadalom potenciális hatását fejezi ki. Ez a másik személy a társadalom jelzése. Ahogy a cselekvő igazodik hozzá, úgy már a társadalmiságot érhetjük tetten. De ez még csak hatás, és nem kölcsönhatás. A társadalmiságban benne rejlő kölcsönösséget, kölcsönhatást, kölcsönös egymáshoz igazodást a társadalmi kapcsolat fogalmával lehet igazán jól megragadni."Társadalmi » kapcsolatról« beszélünk, ha többek magatartása értelmi tartalmának megfelelően kölcsönösen egymáshoz igazodik, és magatartásukat ez a kölcsönös igazodás irányítja." [weber]
A cselekvés és a társadalmi cselekvés fogalmába már bele kellett építeni az ágencia, valamint az intencionalitás minőségét, a most következő feladat a kölcsönösség, és egy kicsit később majd a kölcsönös függőség, az interdependencia összetevéjének felvétele az elméleti keretrendszerbe. Ebben a fejezetben a kölcsönös igazodásnak, egymásra figyelésnek egy különösen fontos esetét vizsgálom meg. Azt a beállítódást elemzem, amely szabályozza bennünk, hogy miként viszonyulunk magunkhoz (Egohoz) és másokhoz, a másikhoz (Alterhez) a cselekvéseink során.Ágensre irányultság: társas preferencia
Ezzel a történettel a közgazdászok nem igazán tudnának mit kezdeni. A közgazdaságtan követőinek túlnyomó részére ugyanis nagyon jellemző az a beállítódás, amely szerint az ember – gazdasági – cselekvését az 'önző ember' hipotézisére támaszkodva lehet (kell) megmagyarázni. Pedig ez nem igaz. Tagadhatatlan, hogy sokszor, nagyon sokszor valóban működőképes a hipotézis. Lehet, hogy az esetek nagyobb részében. Talán. De ugyancsak sokszor, sőt, nagyon sokszor találkozhatunk olyan helyzetekkel, amelyekben önzetlen beállítódások mentén cselekszenek az emberek. A társadalmi cselekvés modelljébe ezt a kétfajta beállítódást mindenképpen fel kell vennünk. De ha már beszélünk önző és önzetlen beállítódásokról, akkor érdemes azt is megvizsgálni, nem lehet-e általánosabban kezelni ezt a kérdést, nem lehet-e egy olyan elméleti keretet felállítani, amelyben az egoizmus és altruizmus is értelmezhető, de a modellbe fel lehet venni további fogalmakat is. A beállítódás, a motiváció fogalmát kell tehát pontosítani, és ezen belül lehet majd értelmezni a cselekvők egymáshoz való viszonyát kifejező fogalmakat. Utóbbiak terjedelme szűkebb a beállítódás általánosabb fogalmának terjedelméhez képest, meg kell tehát mondanunk azt, hogy milyen jellemzők mentén tudjuk meghatározni, tipizálni az ágenciával kapcsolatos beállítódásainkat. A beállítódásaink, motivációink sok esetben abban az értelemben (és irányban) szűkülnek le a cselekvéseink során, hogy gyakran "csak" arra figyelünk, hogy a cselekvéseink következményei hogyan érintik a társadalmi kapcsolat résztvevőit, az ágenseket (Egot és Altert). A kérdés itt az, hogy a cselekvő mennyire veszi figyelembe azt, hogy a döntése (cselekvése) hat(hat) részben saját magára, részben a társára (a másikra, a többiekre). Kézenfekvőnek tűnik erre felállítani azt a fogalmi kettősséget, amely szerint a cselekvő (Ego) lehet önző vagy önzetlen. Ezek a fogalmak azt ragadják meg, hogy a döntés/cselekvés következményei mennyire jók, előnyösek vagy károsak, előnytelenek az Ego, illetve az Alter számára. Ha az Ego a hasznok maximalizálása, illetve a károk minimalizálására törekszik (és csak arra), akkor egoizmusról ('Ego'-izmusról), egoista beállítódásról beszélhetünk, ha döntései során figyelembe veszi Alter szempontjait is, akkor altruizusról ('Alter'-izmusról), altruista beállítódásról. Ha így gondolkozunk, akkor az önző, egoista (selfish, egoist) és az önzetlen, altruista (unselfish, selfless, altruist) beállítódás egymás ellentétének, komplementerének tekinthetjük. Ez az ellentét azonban megszűnik, pontosabban átalakul, ha a másikhoz (Alterhez) való értékviszonyulást úgy kezeljük, hogy eközben figyelünk az értékelés (mint olyan) szükségszerűen bipoláris jellegére. Ha feltételezzük, hogy a döntés/cselekvés nem mindig az Ego és/vagy Alter javára irányulhat, de előfordulhat az is, hogy bizonyos helyzetekben Egonak vagy Alternek (vagy mindkettőnek) kára keletkezik, és ezt a lehetőséget is értékelni akarjuk, akkor a modellünket bővíteni, általánosítani kell ezen a ponton. Ha a bipolaritást figyelembe akarjuk venni, akkor a jóindulatú (benevolent) és rosszindulatú (malevolent) beállítódást kell szembe állítanunk egymással. A jóindulat az ágens javát, a rosszindulat az ágens kárát preferálja. A bipolaritás modellbe emelése magával vonja azt, hogy az egoizmus-altruizmus ellentétpár helyett másfajta kettősséget kell alkalmaznunk. Az ágensre irányultság általános fogalmából kell kiindulnunk. Ennek segítségével a magára irányuló (self-regarding, self-serving), illetve a másikra irányuló (other-regarding, other-directed) fogalmakat használva megragadhatjuk a kétfajta ágens (Ego és Alter) irányába történő viszonyulás mozzanatát. [♦] Ha ki akarjuk fejezni az ágensre irányultság pozitív és negatív típusait, akkor további fogalmakat kell felvennünk. Később részletesebben kifejtem, mivel, miért és hogyan érdemes bővíteni a fogalmi modellünket, de már előzetesen érdemesnek tartom itt jelezni, hogy az Alter felé irányuló rosszindulatú beállítódás jelzésére az agresszió, az Egora vonatkozó rosszindulatra pedig az autoagresszió (önagresszió) fogalmakat vehetjük igénybe. Ha így teszünk, akkor lesz két dimenziónk, az ágensre irányultság, illetve e viszony polaritása, valenciája. A két dimenzió mentén négyfajta beállítódást fejezhetünk ki: ha a jóindulat az Egora irányul, akkor egoizmusról, ha Alterre, altruizmusról, ha a rosszindulat az Egora, agresszivitásról, ha Alterre, autoagresszivitásról beszélhetünk. Kiindulásként felrajzolhatunk egy ábrát, amelyet a későbbiekben még további fogalmakkal kell kiegészíteni.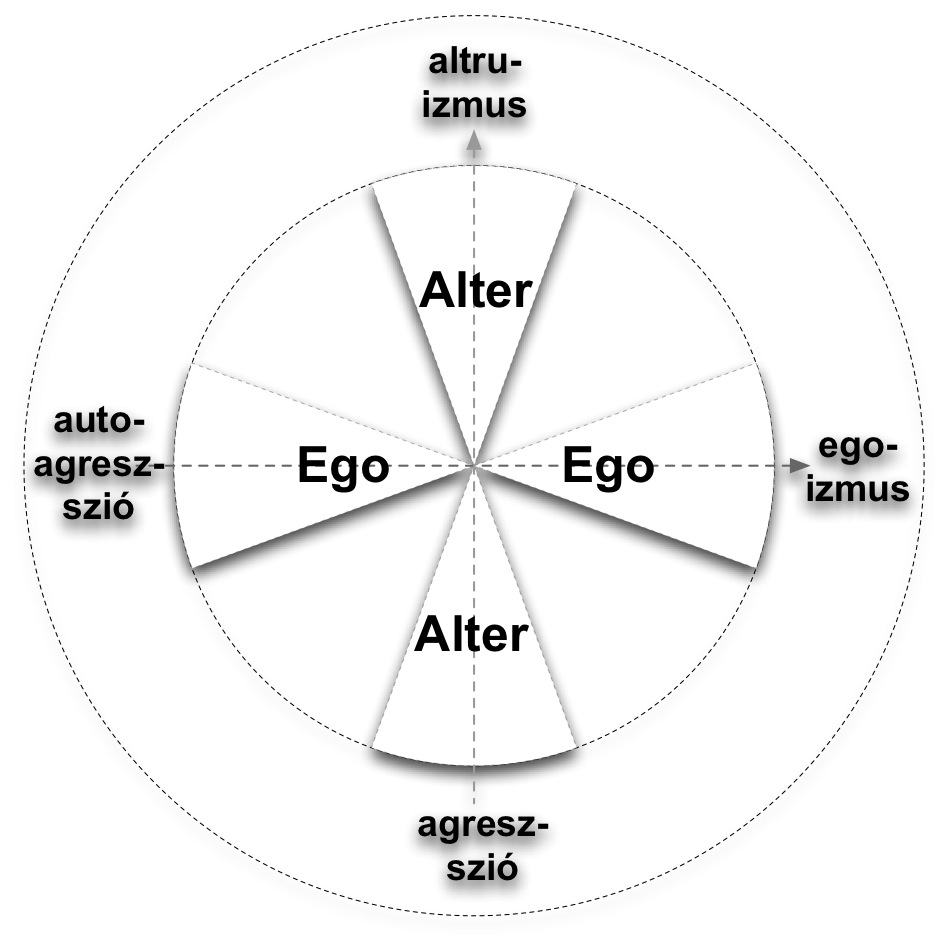
Az ágensre irányuló beállítódások, a szociális preferenciák ábrájára tekintve egyből hiányérzetünk támadhat amiatt, hogy ez a keret olyan fogalmakat határoz meg, amelyek a szociális preferenciák tiszta végpontjait jelentik egy-egy dimenzió mentén, de nem mutat semmit az átmenti állapotokból. Márpedig jogos az a feltételezés, hogy vannak, sőt, sokkal gyakrabban vannak olyan esetek, amikor valakinek a másikhoz való viszonya egy kicsit altruizmusból, egy kicsit egoizmusból áll össze, és van úgy, hogy az ember társas irányultsága olykor a pozitív, máskor inkább a negatív pólushoz áll közelebb valamelyik dimenzióban. Nagyon steril az az elképzelés, ami szerint vagy a más javát (kárát) vagy a saját javamat (káromat) akarhatom. Sokkal életszerűbb azt feltételezni, hogy a döntéseink során valamilyen módon és mértékben egyaránt figyelembe vesszük a magunk és a másik javát (kárát). [♦] Ehhez viszont arra van szükség, hogy a fenti ábrát (és az eddigi modellünket) további fogalmakkal kiegészítsük.
Magasabbrendű beállítódás: büntetni akarás
Az előző fejezetben a szociális preferenciák osztályozásához használható két dimenziót különítettem el. Az értékirányultságok bipoláris jellegének megragadására a jóindulatú, illetve rosszindulatú beállítódások szembeállítását javasoltam, hogy ezáltal definiálhassuk az agresszió (másiknak kárt okozni) és az autoagresszió (magunknak kárt okozni) fogalmát. Később még tárgyalni fogom az agresszivitás jelenségét, és akkor kitérek arra a kérdésre, hogy hol érhetjük tetten és hogyan magyarázhatjuk az agressziót az állati és emberi társadalmakban. Szükségesnek érzem azonban, hogy egy fontos kiegészítést, vagy inkább valamiféle pontosítást tegyek ezen a ponton. Ha ugyanis az agresszivitáson azt értjük, hogy nem az ágens javát, hanem kárát akarja valaki, akkor e jelenség létezését sok esetben csak úgy tudjuk megmagyarázni, ha figyelembe vesszük azt a tényt, hogy az ember büntetni akarja magát és/vagy a másikat. Ha azonban a büntetés jelenségét is figyelembe vesszük itt, akkor az agresszivitás és a rosszindulat kapcsolatáról is kicsit másként kell gondolkoznunk. A társadalmi cselekvésekről szólva korábban már említettem, hogy a cselekvés fogalmát magasabb rendben is értelmezhetjük. A tartózkodást mint negatív cselekvést például másodrendű fogalomként kell kezelnünk (☜) de elképzelhető más eset is. Amikor az emberek szankcionálják, büntetik vagy jutalmazzák a másikat, akkor az ilyen cselekvéseket magasabbrendű fogalmakkal írhatjuk le, mert önmagukban nem értelmezhetők, csak akkor, ha valamilyen másik cselekvésre "vonatkoztatjuk". A büntetés viszont a legtöbb esetben valamiféle agresszió alkalmazását jelenti. Ebben nem különbözik a "sima" agressziótól. A büntető beállítódásában viszont lényeges különbség figyelhető meg: a büntető jóindulat mentén büntet, azaz saját büntető cselekvését jónak tartja. Kárt okoz a büntetett félnek, de ez a károkozás más. Erről a fontos szemléletváltásról később még hozok példákat, a fogalmi elemzésben is mélyebben kitérek a problémára, itt csak azt akarom jelezni, hogy az agresszivitás jelenségét, az agresszív beállítódások létezését elég gyakran (bár nem mindig) a büntetési szándékkal tudjuk megmagyarázni. Azt is később fogom elemezni, hogy a büntetés, akár úgy értelmezzük, mint egyfajta beállítódást, akár úgy, mint egyfajta cselekvést, logikai értelemben magasabbrendű fogalomnak számít.Társas értékorientáció
A korábbiakban felvettem a modellbe azt a két dimeziót, amelyek mentén leírhatjuk a szociális preferenciákat. Az ágensre irányultság, valamint az értékpolaritás tengelyei mentén négy "szélsőértéket" definálhatunk: egoizmust, altruizmust, agressziót és autoagressziót. Következő lépésként bővíteni szeretném a társas motivációk fogalmi modelljét. Ezen a ponton azonban egy – talán – szokatlan módszertani probléma nehezíti a továbblépést. A szociális preferenciák modelljének kiegészítése során a társas értékorientáció (social value orientation, SVO) elméletének eredményeit szeretném használni úgy, hogy a fogalmi építkezés logikáját ne törjem meg ezzel. A társas értékorientáció elmélete alkalmas erre, mert zökkenőmentes továbblépést biztosít. Egy olyan módszertant ad a kezünkbe, amely segítségével kísérleti úton lehet mérni az emberek társas beállítódásának irányát és mértékét (minőségét, mennyiségét). Történelmi tény viszont, hogy az egész elmélet azzal a céllal jött létre, hogy valahogy meg lehessen szabadítani a kísérleti mérési szituációkat az ún. interdependencia jelenségétől azért, hogy csak az egyéni cselekvők beállítódásait tudjuk tisztán mérni. Hogy az interdependencia pontosan mit jelent, és miért kell kilépni az ilyen helyzetekből, azt a játékelmélet alapfogalmainak ismeretében lehet elmagyarázni. Ezt viszont – a fogalmi modellezés építkezési logikája miatt – csak jóval később tudom megtenni. Ezt a problémát úgy tudom csak feloldani, hogy nagyon röviden itt is el fogom mondani azt, amit tudni kell a játékelméleti helyzetek leírásáról, hogy érteni lehessen a társas értékorientáció elméletének kapcsolódását a játékelmélethez. A társas értékorientáció elméletének alapjait David M. Messick és Charles G. McClintock fektették le 1968-ban megjelent cikkükben [Messi] A tanulmányból két fontos eredményt érdemes megemlíteni. Egyfelől elkülönítettek háromféle társas értékorientációt egymástól, amelyeket individuális, kooperatív és versengő irányultságnak neveztek. Az individuális beállítódású ember csak a saját hasznát (own gain) nézi a döntései során, a kooperatív ember a maga és a társa együttes hasznát akarja maximalizálni (joint gain), míg a versengő típus arra tör, hogy minél nagyobb legyen kettejük közti különbség a maga javára (relative gain). Egy példát mutatva erre az alábbi táblázatban azt ábrázolhatjuk, hogy a vizsgált alany (Ego) két döntési lehetőség közül választhat (X és Y), mindkét alternatívában a maga és a társa számára lehetséges kifizetéseket hasonlítja össze.| $X$ | $Y$ | |||||||||||||
| Ego kifizetése | 5 | 8 | ||||||||||||
| Alter kifizetése | 2 | 6 | ||||||||||||
| $\rightarrowtail$ |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| $\rightarrowtail$ |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| individualizmus | saját nyeremény maximuma | max($Ego$) | (100 | 70) | ||||||||||
| kooperáció | együttes nyeremény maximuma | max($Ego$+$Alter$) | (90 | 90) | ||||||||||
| versengés | nyereménykülönbözet maximuma | max($Ego$-$Alter$) | (80 | 40) | ||||||||||
| altruizmus | másik nyereményének maximuma | max($Alter$) | (70 | 100) | ||||||||||
A modell bővítésének szükségességét elfogadva, de az alkalmazott terminusokat kicserélve a korábban már bemutatott, általam preferált terminusokra, az alábbi táblázatba rendezhetjük az új kategóriákat.
| autoagresszív (mazochizmus) | saját nyeremény minimuma | min($Ego$) | (10 | 50) | ||||||||||
| destrukció (szadomazochizmus) | együttes nyeremény minimuma | min($Ego$+$Alter$) | (20 | 30) | ||||||||||
| önfeláldozás (mártíromság) | nyereménykülönbözet minimuma | min($Ego$-$Alter$) | (30 | 80) | ||||||||||
| agresszió (szadizmus) | másik nyereményének minimuma | min($Alter$) | (50 | 20) | ||||||||||
| (100 | 70) | egoizmus | max(Ego) | |||||||||||
| (90 | 90) | kooperáció | max(Ego+Alter) | |||||||||||
| (80 | 40) | versengés | max(Ego-Alter) | |||||||||||
| (70 | 100) | altruizmus | max(Alter) | |||||||||||
| (10 | 50) | autoagresszió | min(Ego) | |||||||||||
| (20 | 30) | destrukció | min(Ego+Alter) | |||||||||||
| (30 | 80) | önfeláldozás | min(Ego-Alter) | |||||||||||
| (50 | 20) | agresszió | min(Alter) | |||||||||||
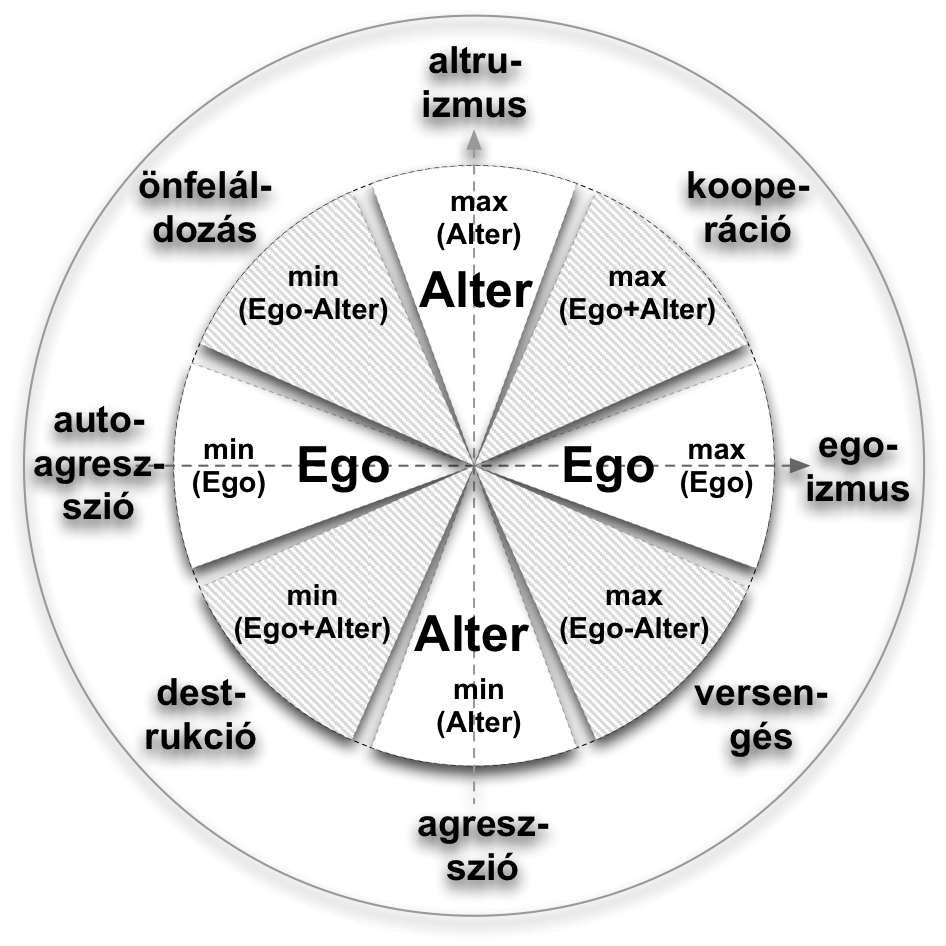
Bár ezt a nyolcas tagolású felbontást nem tudom teljes mértékben kihasználni a későbbiekben, az elméleti teljesség miatt meghagyom így a modellben. A játékelméleti fejezetbe "csak annyit" viszek tovább belőle, hogy akkor majd megengedem, sőt, tudatosan alkalmazni fogom azt, hogy a játékosok nemcsak proszelf (egoista vagy versengő) beállítódással játszhassák a játékaikat, de proszociálisak (altruisták vagy kooperatívak) is lehessenek. Ez a kettőség viszont felvet egy további komoly kérdést. Ha elfogadjuk, hogy a – játékelmélettel leírt – társadalmi helyzetekben különböző társas motivációkkal lépnek be emberek, akkor ezt a különbözőséget, az irányultságok, a társas preferenciák különbözőségeit meg kell tudnunk ragadni a fogalmi modellünkben is. Ehhez – Franz Dietrich és Christian List javaslatát megfogadva – kettős ontológiát (esetleg többes ontológiát) kell kezelnünk, hogy egyszerre leírhassuk, értelmezhessük a játékosok (és a kívülálló modellezők, megfigyelők) különböző beállítódásait ugyanazon játékszituációra vonatkozóan.
" … a preferencia kialakulását leíró, tulajdonság-alapú beszámolónkat újraformálhatjuk mint kettős-ontológiai leírást, amelyben az ágens alternatíváinak ontológiáját elkülönítjük a megfigyelőétől." [Franz]
A nagy kérdés itt az, hogy miként akarjuk modellezni a társas preferenciákat. Ha azt állítjuk, hogy a cselekvő, az Ego proszociális értékekkel rendelkezik, akkor ezt hogyan írjuk le? Nem is az az igazi kérdés itt, hogy milyen súlyokat rendeljünk a magára irányuló, illetve másikra irányuló beállítódások erősségének kifejezésére, hanem az, hogy mit fejezünk ki pontosan a proszociális motívumokkal. Az Ego vagy a megfigyelő vagy az Alter véleménye, preferenciarendezése számít-e ilyenkor? A különböző válaszok esetén mást és mást kell majd a proszociális irányultságokat leíró formulákba, képletekbe beírni. A társas értékorientációval kapcsolatos fogalmakat két szinten vizsgálhatjuk: a tényleges cselekvések szintjén, illetve a cselekvésekkel kapcsolatos motivációk, irányultságok szintjén [Ellio] Az altruista minősítéhez hozzátartozik egyfelől Ego olyan cselekvése, amely Alter számára előnyös, Egonak költsége (vagy elmaradt haszna) volt vele, viszont azt is "elvárjuk", hogy másfelől Ego altruista motiváció miatt tegye meg azt, amit megtesz. Valaki csinálhat olyat, amivel másnak kedvez, magának árt, de ha ezt öngyűlöletből vagy önbecsülés hiányából teszi, akkor ezt nem nevezhetjük altruizmusnak [Pierr] Az egoizmus minden késztetést, minden vágyat magára irányulónak tekint, az altruizmushoz "elegendő" egy másikra irányuló késztetés, vágy léte, és már beszélhetünk róla. Ez módszertanilag fontos különbséget takar a két fogalom között. Az egoista beállítódás magára irányul, azzal nincs elméleti kiterjesztési probléma. A másikra irányuló orientáció esetében azonban felmerül a kérdés, hogy lehet-e, érdemes-e tágítani a 'másik' fogalmának terjedelmét. Az általam kifejtett megközelítésben a 'másik' egy 'ágens'. A cselekvéselmélet számára ez az értelmezés elegendő. Elméletileg lehetne tágítani ezen az értelemzésen, ha megengednénk, hogy a 'másikra irányulás' lehessen egy eszme, az emberiség egésze, a Föld stb. Angolul ezekre lehetne az irányultságokra a 'selfless' terminust alkalmazni, magyarul nem tudok ennek megfelelőjéről. Korábban bemutattam, hogy miként definiálta Sober és Wilson a végső és instrumentális vágyak fogalmát (☜) Soberék a vágyfogalmak tisztázása után definiáltak három motivációfogalmat is [Ellio] amelyek közül kettő már itt is szóba került. Az egoizmus és altruizmus mellett harmadik kategóriaként vezették be a hedonizmus fogalmát. Az egoizmust, illetve altruizmust magára irányuló (☜) az altruizmust másra irányuló végső vágyként definálták, a hedonizmust pedig – az egoizmus alá rendelve – olyan vágyként határozták meg, amely az élvezet megszerzésére és a fájdalom elkerülésére irányul. Akkor beszélhetünk egyáltalán egoizmusról vagy altruizmusról, amikor az egyén saját érdekei és a releváns másik (mások) érdekei keresztezik egymást. Ilyen esetekben az altruizmus mások érdekét saját költségén támogató cselekvést jelent, az egoizmust viszont a saját érdeket mások költségén való követésével ragadhatjuk meg. Mivel ekkor két személy közti kapcsolatot elemzünk, mondhatjuk azt, hogy interperszonális önzésről, illetve interperszonális önzetlenségről van itt szó. Ennek analógiájára bevezethetnénk egy új fogalomkettőst, amit Pierre Le Morvan javasolt, és ami ugyanazon személy jelenbeli és jövőbeli érdekei között konfliktusok esetén használható, vagis intraperszonális kategóriákról, az intraperszonális önzésről, illetve intraperszonális önzetlenségről lehetne szó [Pierr] Bár megfontolandó maga ez a javaslat is, én itt inkább csak azt emelném át saját modellembe, amit Le Morvan a szükséges feltételek kapcsán dolgozott ki. Az egyszerűség és az összehasonlítás kedvéért mondhatjuk azt, hogy az önző saját, az altruista a másik érdekét elégíti ki, akkor az előbbi önérdekkövető, az utóbbi másérdekkövető, tehát van önérdek és másérdek. Ennek analógiájára nevezzük a jelenbeli érdeket jelenérdeknek, a jövőbelit pedig jövőérdeknek (ez utóbbi két kategóriát nyilván az intraperszonális attitűdökhöz rendelhetjük). Az új terminusok segítségével egyszerre fejezhetjük ki azt a három feltételt, amit Le Morvan rögzített az altruizmus és egoizmus elkülöníthetőségével kapcsolatban.| divergencia feltétel | legyen különbség, konfliktus az önérdek/jelenérdek és a másérdek/ jövőérdek között | |||||||||||||
| költségterhelési feltétel | az egyén előtt legyen választási lehetőség abban, hogy a önérdekét/jelenérdekét követi-e a másérdek/jövőérdek rovására vagy fordítva | |||||||||||||
| értékelési feltétel | az egyén számára legyenek olyan esetek, amikor a másérdek/jövőérdek kárára hozott önérdek/jelenérdek melletti döntés morálisan rossznak ítélhető, illetve a másérdek/jövőérdek támogatása az önérdek/jelenérdekkel szemben morális jónak tartható | |||||||||||||
Egoizmus
"Az ebédünket nem a mészáros, a sörfőző vagy a pék jóakaratától várjuk, hanem attól, hogy ezek a saját érdekeiket tartják szem előtt. Nem emberségükhöz, hanem önszeretetükhöz fordulunk, és sohasem a magunk szükségéről, hanem a rájuk váró előnyökről beszélünk nekik." [Smith]
Az Adam Smith által sugallt társadalomkép azonban egyoldalú, hiányos, szükség van a korrekciójára. Még akkor is szükséges módosítani ezen az elfogult szemléleten, ha közben elfogadjuk azt a tézist, miszerint a fogalmi építkezésben az egoizmus kategóriáját elsődlegesnek kell tartanunk az altruizmus fogalmához képest abban az értelemben, hogy az utóbbi csak az előbbi létezése esetén képzelhető el. Ezt Jon Elster a következőképpen indokolta."Bizonyos értelemben az önérdek … alapvetőbb, mint az altruizmus. A természeti állapot – jóllehet gondolatkísérlet – logikailag koherens helyzet. Olyan világot viszont nem tudunk logikailag koherensen elképzelni, amelyben mindenkinek kizárólag altruista indítékai vannak. … Ha senkinek sem lennének elsőfokú, önző örömei, senkinek sem lehetnének magasabb rendű, altruista indítékai sem. … Ez tisztán logikai kérdés. Ahhoz, hogy egyesek altruisták lehessenek, másoknak legalább időnként önzőnek kell lenniük, de mindenki mindig lehetne önző. … De ebből – sem általában, se bármely adott esetben – nem vonhatjuk le azt a következtetést, hogy az önzés a legelterjedtebb motiváció." [elste]
Nem tudom, mi alapján, hogyan lehetne mérni, vajon melyik lehet a legelterjedtebb emberi motiváció. Én mind a kérdésfeltevést, mind a válaszkísérleteket hanyagolnám. Nem vitatnám az egoista beállítódás létét, sőt, elsődlegességét, inkább csak a kizárólagosságát. A tisztább kép kialakítása érdekében először az egoizmus fogalmát érdemes alaposabban megvizsgálni. Kiindulhatunk abból a meglepő és provokáló kérdésből, amit Andrew Oldenquist tett fel, hogy ti. hogyan lehetséges egyáltalán az önzés mint olyan [Andre] Még mielőtt bármit is bemutatnék Oldenquist gondolatmenetéből, tisztázni szeretném, hogy Oldenquist nem kérdőjelezi meg az önzés létezését (és elterjedtségét), csak azt próbálja meg tisztázni, hogy milyen feltételek mentén beszélhetünk önzésről abban az értelemben, ahogy a hétköznapi beszédben használjuk ezt a fogalmat. Mindenesetre erős állítással kezdi tanulmányát." … a célkövető entitások "természetes állapota" a kantiánus, altruista vezérelv szerinti cselekvés, az egoizmusra jóval nehezebb magyarázatot adni, mint az altruizmusra." [Andre]
Oldenquist azzal indít, hogy képzeljük el két embert, Robert Kraut$_1$-ot (K$_1$) és Robert Kraut$_2$-ot (K$_2$), akik – klónozás eredményeként – minden tulajdonságukban megegyeznek, és a környezetüktől is ugyanazokat az ingereket kapták. kapják. Mi történik – teszi fel a kérdés Oldenquist –, ha mindkét ágensnek fájni kezd a foga, de csak egyikük kezelésére van mód. Mi, akik "kívülről" figyeljük a dolgokat, nem tudunk egyik ágens érdekében sem dönteni, hiszen nem látunk semmi különbséget köztük. Ha közöljük az érintettekkel is, hogy csak egyikük kaphat kezelést, és K$_1$ úgy reagál erre, hogy neki kell kapnia a kezelést, akkor azt mondhatjuk, hogy egoista módon cselekedett. Ő különbséget tud tenni a saját és a társa fájdalma között, és saját fájdalmának a megszüntetését előbbre tartja, mint a másik kezelését. Eddig plauzibilisnek tűnik a dolog, de Oldenquist mégis ezen a ponton tartja szükségesnek, hogy tisztáza, mit is jelent pontosan az egoizmus és altruizmus fogalma, és a különbséget a hozzájuk kapcsolható szelf fogalom két különböző értelmezésében látja. A kétféle értelmezést így írja le.
"Az egoizmus azon alapul, amit a partikuláris szelf fogalmának fogok nevezni. Ez rendelkezik azzal a képességgel, hogy különbséget tudjon tenni partikuláris dolgok között, amelyek lehetnek akár teljesen hasonlóak is, azonosítani tudja magát mint egyetlent a többi közül, és képes erre a megkülönböztetésre alapozni saját akaratait, értékeléseit és viselkedési szabályait. …
… az altruizmus … vagy … imperszonális moralitás azon alapul, amit valamely fajta szelf (egy példánya) fogalmának fogok nevezni. Ekkor, ha valamit értékelni kell, K$_1$ úgy tekint magára, mint akinek olyan tulajdonságai vannak, amelyekkel – elvileg – K$_2$ vagy bárki más is rendelkezhetne."
[Andre]
Altruizmus
Az emberiség különböző – tudományos, vallási, művészeti, erkölcsi – diskurzusaiban mindig is kiemelt helyet kapott az önzetlenség, az altruizmus kérdése. Itt én csak az altruizmus fogalmi elemzését, összetevőinek, tipizálási lehetőségeinek bemutatását szeretném elvégezni, és nem foglalkozom az altruizmus kialakulásának és fenntartásának biológiai, illetve társadalmi mechanizmusaival. Az altruizmussal kapcsolatos vizsgálatok, kísérletek első körének áttekintését nyújtja Dennis L. Krebs cikke [Krebs] majd két évtized évtizeddel később teszi meg ugyanezt E. Midlarsky és E. Kahana [Midla] illetve Jane Allyn Piliavin és Hong-Wen Charng tanulmánya [JaneA] arról pedig, hogy az altruizmus hogyan jelenik meg a különböző kultúrákban, Herbert Gintis ad alapos áttekintést egy cikkében [Herbe] [♦] A közgazdasági imperializmus egyik legszebb példájaként lehet hivatkozni Gary Becker vásott kölyök modelljére (Rotten kid theorem), amelyben Becker a családi kapcsolatokat jellemző altruizmus jelenségét írta le formális eszközökkel [becke] [♦] A méltányosságelméletekben (☜) az alkujátékok vizsgálataiban (☜) voltaképp az altruizmus létét, erősségét keresik, mérik, magyarázzák. Ezekkel az elméletekkel, elemzésekkel máshol foglalkozom, ezért itt nem térek ki rájuk. Nagyon változó, hogy mikor beszélnek kooperációról és mikor altruizmusról az ide tartozó biológiai jelenségek elemzéseiben, én a kooperáció kapcsán fogom röviden ismertetni ezeket az eredményeket, de az altruizmus fogalmához rendelten is ugyanúgy be lehetne mutatni ezeket. [♦] Az altruizmus kapcsán mindenekelőtt arra hívnám fel a figyelmet, hogy ez a fogalom bizonyos értelemben elméleti konstrukció, nehéz elképzelni a tiszta altruizmus gyakorlati megvalósulását. Nem arra gondolok, hogy ideáltipikus fogalmi konstrukció lévén a tényleges gyakorlatban nem találhatjuk meg az elméletben elképzelt jelenséget, hanem arra, hogy én nem nagyon tudok elképzelni olyan esetet, amiben az Ego a cselekvésével úgy tud a másiknak, Alternek előnyt okozni, hogy eközben semmilyen értelemben nem változik a saját (Ego) helyzete, sem előnye, sem hátránya, költsége nem származik a dologból. Ha egyszer mindig adott értéktérben valósítjuk meg a cselekvéseinket, akkor nehezen tudom elképzelni az önmagunkra vetítve teljesen értékmentes cselekvést. Elméletileg persze elképzelhető, hogy nincs költsége valakinek, miközben a másik számára előnyt biztosít a cselekvésével. Ha olyan helyzetet képzelünk el, amelyben az Ego számára két döntési lehetőség van, és mindkettő alternatíva ugyanazt a eredményezi maga számára, viszont az Alter számára Ego egyik döntése előnyös, a másik hátrányos lenne, akkor mondhatjuk azt, hogy az Alter számára előnyös döntés Ego Alterrel szembeni altruizmusát mutatná, hiszen saját szempontjait tekintve voltaképp nem lenne döntési helyzetben, a döntése igazából az Alterhez való viszonyát érintené. Az ilyen elméleti lehetőségre azonban nem nagyon tudok tényleges gyakorlati példával szolgálni. Az altruizmus másik fontos vonása az, hogy szükségszerűen másodrendű fogalom. Akárhogyan is definiáljuk az altruizmus fogalmát (az értékek, a hasznosságérzetek, a kifizetések fogalmaira támaszkodva), a másikra irányultság lényegi mozzanatát csak úgy vehetjük figyelembe, hogy az Ego értékelésébe (hasznosságérzetébe, kifizetésébe) belekalkuláljuk Alter értékelését (hasznosságérzetét, kifizetését). Ez a beágyazottság mindenképpen másodrendűvé teszi a fogalmat. [♦] Kristen Renwick Monroe azt javasolja, hogy az altruizmust olyan viselkedésként definiáljuk, ami valaki másnak okoz előnyöket úgy, hogy közben a cselekvő számára bizonyos költséggel, lemondással, esetleg valamilyen kockázattal jár [Krist] Monroe azt is kiemeli, hogy melyek a definíciójának lényegi elemei, amelyek hiányában nem beszélhetünk igazi altruizmusról. Előszöris az altruizmushoz mindig cselekvés szükséges, tehát nem elégséges valamiféle jószándék, egy nemes gondolat kifejezése. Másodszor az altruista cselekedetnek elsősorban kell a másik javára irányulónak lennie, tehát ha egy egoista cselekedet másodlagos hatásaként előnyök keletkeznek a másik számára is, akkor Monroe szerint nem beszélhetünk altruizmusról. Harmadszor a szándékok fontosabbak, mint a tényleges következmények. Ha valaki jót akar tenni valakinek, de – mindegy, milyen okok miatt – balul sül el a dolog, vagy a kezdetben előnyösnek látszó következmények esetleg hosszútávon már hátrányosakká válnak, attól még nem lehet megkérdőjelezni az eredeti szándék és cselekedet altruista jellegét. Végül, negyedszer az altruista tettnek valamilyen módon csökkentenie kell a cselekvő jólétét, hasznosságát, erőforrásait, tehát valamilyen költséggel kell járnia. Ha ilyesmi nincs, vagy még inkább, ha a cselekedet nemcsak a másik, de a cselekvő számára is előnyökkel jár, akkor az a kölcsönös előnyök, a kollektív jólét, a kooperáció, a harmónia világába tartozik. Elias L. Khalil egy nagyon alapos tanulmányában úgy definiálja az altruizmus fogalmát, hogy azt a jótékonyság, önkéntes (és névtelen) adományozás (charity) fogalmával kapcsolja össze, miközben kizár egy sor olyan értelmezési lehetőséget, amelyeket elég sokszor és elég sokan az altruizmus fogalma alá szoktak sorolni [Elias] Előbb ez utóbbiakat veszem sorba. Khalil szerint létezik három – interakció alapú – értelmezés, ami nem tartható altruizmusnak. Az első az egoista altruizmus, ami az altruista cselekvést a várható jövőbeni haszonnal magyarázza. Erre lehet példa a direkt reciprocitás jelensége, amit a játékelmélet is sokat elemzett (☜) Ez a értelmezés párhuzamba állítható az evolúcióbiológiából származó, triversi reciprock altruizmus fogalmával (☜) Khalil szerint ez a jelenség azért nem tartató altruizmusnak, mert itt csak arról van szó, hogy a jövőbeni viszonzásért cserébe, tehát a jövőbeni előnyökért hajlandók vagyunk a jelenben áldozatokat hozni a másikért. A második – Khalil által az altruizmusból kizárt – felfogás az egocentrikus altruizmus. Akkor beszélhetünk erről, ha az Ego abból eredő hasznosságérzete, hogy élvezi Alter hasznát/örömét valami jószág elfogyasztásakor, nagyobb, mint az a hasznosság, mint amit Ego az adott jószág saját fogyasztása révén érhetne el. Ilyen az anya öröme a gyereke boldogsága miatt. Többet ér az anya számára az, ha a gyerekét látja örülni, ezért nem magának vesz meg egy új cipőt, hanem a gyerekének egy játékot. Ez a helyettesítő élvezet (vicarious pleasure), az Alter öröméből Egonak jutó rész – Khalil szerint – ugyanúgy működik, mint a biológiában a rokoni kiválasztás hamiltoni mechanizmusa (☜) A harmadik téves altruizmusfelfogásként Khalil az altercentrikus altruizmust nevezi meg. E felfogás szerint vannak proszociális jegyeink, amelyek arra késztetnek minket, hogy támogassuk a velünk valamiért egy csoportba sorolt társainkat. E jelenség biológiai párhuzamaként a csoportszelekciót jelölhetjük meg (☜) Nem kell itt genetikailag örökölt morális gén létezését feltételezni, elég csak a tanult, kulturális mechanizmusokon keresztül belénk nevelt viselkedési mintákra gondolni. Ezzel, Khalil szerint, az a baj, hogy egybemossa az altruizmus és a becsület(esség) jelenségét. A második körben Khalil bemutat három olyan altruizmusértelmezési lehetőséget, amelyeket közösen normatív felfogásnak nevez, és amelyek mindegyikét ki is zárja az elfogadható altruizmusértelmezések köréből. A különböző interpretációk mögötti elméletek közül az első a kantiánus megközelítésen alapuló etikai elmélet, a második a szimbolikus interakcionizmushoz köthető szocializációs vagy kulturalizációs elmélet, a harmadik pedig a pszichológiai megközelítésű melegségvágy elmélet. Az etikai megközelítés pédájaként Khalil Amitai Etzioni könyvére hivatkozik, ami a szerző által a közgazdaságtan számára ajánlott új szempont, a morális dimenzió figyelembevételének a szükségességéről szól [Amita] Ez az elmélet sokban hasonlít ugyan az altercentrikus megközelítésre, de az megkülönbözteti őket, hogy az altercentrikus hozzáállás mindig valamilyen választott szempont szerint (például a másik jólétét szem előtt tartva) igazodik a másikhoz, az Alterhez, míg a kantiánus elv minden szempontból, tehát szempontoktól függetlenül egyenlően kezeli a másik embert, amikor nem engedi meg nekünk, hogy bárki mást eszközként kezeljünk saját cselekvésünk során. Etzioni ezt az elvet úgy modellezi, hogy a szokásos értelemben vett, az élvezettel összekapcsolható hasznosság fogalma mellé felvesz egy másik kategóriát is, amit morális hasznosságnak nevez el. Ez a kétféle hasznosságérzet egyszerre hajtja az embert. A szocializációs elméletek legfőbb képviselőjeként George Herbert Meadre hivatkozik Khalil, aki az altruista személetmód kialakulásának okát a nevelésben, szocializációban látja [mead:] A melegségvágy elmélet kidolgozója, James Andreoni szerint nem a másik jólétének növelése, hanem az adakozás vágya hajtja az embereket az altruista cselekedetek felé. Azért tesznek így, mert a segítségnyújtás után érzett belső melegségre (warm-glow) vágynak [Andre] Khalil e háromféle altruizmusmagyarázat egyikét sem fogadja el mondván, hogy ezek nem minden mástól független, belső motiváción, hanem valamilyen másfajta ösztönzésen alapulnak. Utolsó körben Khalil példákat mutat arra, hogy mit is tart igazából altruizmusnak, és – ahogy azt már említettem – kijelenti, hogy akkor és csak akkor beszélhetünk altruizmusról, ha az jótékonyságból fakad. Amikor az emberek névtelenül adományokat küldenek az arra rászorulóknak úgy, hogy tettüknek semmifajta elismerésére nem számíthatnak, amikor tisztán csak a másik ember segítésének szándéka mozgatja őket, akkor beszélhetünk – Khalil szerint – igazi altruizmusról. Végezetül – a félreérthetőség elkerülése érdekében – elkülöníti, pontosabban leválasztja az altruizmus jelenségéről egyfelől a családon belüli szülői altruizmus, másfelől a filantrópia, emberszeretet kérdését. Khalil is azt mondja, sokan másik is vallják ezt, hogy az altruizmus sok esetben nem más, mint hosszútávú egoizmus. Az anya azért segít gyermekének, mert arra számít, hogy ezt majd visszakapja, amikor öreg lesz, és támogatásra szorul. Bár úgy vélem, hogy az emberi motivációk nem képesek ilyen hosszú léptékekben érdemben befolyásolni minket, ezért én értelmesnek tartom "igazi" altruizmusnak tartani ez ilyenféle hosszútávú egoizmust is, de van egy ennél még fontosabb érvem arra vonatkozóan, hogy érdemes, sőt, el kell különíteni két fogalmat egymástól. Mégha hosszútávú egoizmusként is értelmezzük az altruizmust, akkor is szükségünk van arra, hogy a rövidtávú és hosszútávú egoizmusokat el tudjuk különíteni egymástól. Az ugyanis tény, hogy ugyanazokba a helyzetekbe kétféle beállítódás mentén lépnek bele az emberek, jelen időben egoista és jelen időben altruista módon, és ha utóbbira azt mondjuk, hogy ez a jelenidejű altruizmus valójában csak hosszútávú egoizmusként értelmezhető, akkor is meg kell tudnunk ragadni a jelenben eltérő kétféle beállítódást. Ez pedig azt követeli tőlünk, hogy továbbra is fenntartsunk kétféle fogalmat erre a kétféle jelenségre. Ha az adott kontextusban nem zavaró, akkor továbbra is megtarthatónak vélem az eredeti altruizmus-egoizmus fogalomkettőst, és csak akkor alkalmazom a hosszútávú minősítéssel ellátott egoizmus terminusát, ha ezt valamely kontextus megkívánja. Amikor Oldenquist a csoportönzés fogalmáról írt (☜) akkor azt állította, hogy a csoport tagja egymással szemben altruista módon viselkednek, viszont a csoport határain kívüli kapcsolataikban egoistákká válnak. Egészen más irányból tekintett ugyanarra a jelenségre, mégis hasonló eredményre jutott Garret Hardin, aki bevezette a diszkriminatív altruizmus fogalmát [ghard] Hardin alaptézise az volt, hogy nem lehet univerzális értelemben altruizmusról beszélni, az altruizmus megnyilvánulásához mindig szükség van arra, hogy diszkrimináljunk, vagyis valamilyen hatókörön, valamilyen csoporton belül érvényesítsük ezt a politikát, amihez természetesen hozzátartozik az is, hogy a hatókörön, a csoporton kívül felhagyunk az altruizmusunkkal. A diszkriminatív altruizmus fogalma abban az értelemben is termékeny kategória, hogy a fogalomra támaszkodva könnyen képezhetünk egy nagyon plauzubilis tipológiát. Bár Hardin olykor talán suta, kicsit nehézkes terminológiai megoldásokat választott, de tartalmilag nagyon kézenfekvő, a valós társadalmi gakorlatokat jól jellemző altruizmustipizálást javasolt.- individuum
- család
- bajtársiság, kronizmus
- tribalizmus, törzsiség
- hazafiság, patriotizmus
Kooperáció és versengés
Az egoizmus és az altruizmus fogalmainak tisztázására irányuló diskurzusban is felbukkan a kooperációs és a versengés kategóriája, de az igazi "karriert saját jogon" érte el ez utóbbi két fogalom, amihez a fókuszt és a keretet a játékelmélet biztosította (☜) A dolgokat kissé leegyszerűsítve mondhatjuk, hogy elindulása után elég hamar a játékelmélet egyik fő kérdésévé vált, hogy mikor, milyen társadalmi helyzetekben (játékokban) várhatunk kooperatív vagy versengő magatartást a résztvevőktől (játékosoktól), illetve miként lehet biztosítani a kooperációt azokban a játékokban, amelyekre alapértelmezés szerint a versengés jellemző. A játékelméletben azonban nem vagy csak kevesebbet foglalkoztak a kooperáció és versengés, valamit az altruizmus és egoizmus egymáshoz való viszonyával. Mivel a játékelméleti fejezetben sok szó esik majd a kooperáció és versengés problémaköréről, az ezeket biztosító mechanizmusokról, itt inkább a fogalmak jelentésének tisztázására törekszem. A kooperáció értékelésekor kétféle téves nézet tapasztalható. Mivel az altruizmus és az egoizmus "között" helyezkedik el félúton, ezért mindkét irányból a kooperációra tekintve könnyen az ellentétes pólushoz tartozónak lehet minősíteni azt. Mindkét besorolás egyoldalú lenne. A kooperáció lényege pont a kettős természetében jelölhető meg. Tulajdonképpen nem ad semmi újat az a felosztás, ami a nemzetközi kapcsolatok elemzésének világából származik [After] mégis segíthet minket abban, hogy a kooperáció igazi értelmét megtalálhassuk. A nemzetközi kapcsolatokban három kapcsolattípust különítenek el egymástól: a viszályt (dischord), a harmóniát (harmony) és a kooperációt (cooperation). A három fogalom értelmezése eléggé adja magát: harmónia esetén a felek érdekei konfliktusmentesen illeszkednek egymáshoz, míg a viszály esetén az érdekek ellentétesek, vagyis teljes az érdekütközés, végül a kooperáció azt jelenti, hogy a feleknek vannak egymással összeegyeztethető érdekeik, és ezek fontosabbak a többi – konfliktusos viszonyban levő – érdekhez képest. Ezt a hármas tagolás egy dimenzióban kiegészíthetjük Anatol Rapoport javaslatával [Anato] aki szerint a konfliktus (vagy az előző felosztás szerint a viszály) lehet harc (háború, verekedés), amikor erőszakos eszközöket alkalmazva próbáljuk meg a másikat legyőzni, lehet játszma (játék, önérdekkövetés), amikor erőszak nélkül, a másikkal versengve próbáljuk meg legyőzni, megelőzni őt, illetve lehet vita, amikor meggyőződéseket ütköztetve próbáljuk meg a másikat meggyőzni (ekkor már csak kommunikatív cselekvésről lehet szó). Ezt a kiegészítést egyelőre csak az elméleti teljeség igénye miatt tettem meg, gyakorlati segítséget nem jelent a kooperáció fogalmának tisztázása érdekében. A kooperáció jelenségét jobban megérthetjük, ha azt a harmónia vagy a kölcsönyös előnyök (mutualizmus), illetve a viszály (konfliktus) jelenségeihez képest próbáljuk meg elhelyezni a fogalmi térben. Ha a kooperációt úgy értelmezzük, hogy abban mind az Egonak, mind az Alternek előnyei származnak (hiszen a kooperáció az egoizmus-altruizmus tengelyek pozitív értéktartományában helyezkedik el), akkor a kooperációt a harmóniához közelebb álló fogalomnak kell tartanunk. Ha viszont arra gondolunk, hogy bár a kooperációban mindkét ágens számára előnyös, de Egonak egy ilyen helyzet kevesebb nyereséggel, s ebben az értelemben veszteséggel jár a "tiszta" egoizmust megvalósító magatartáshoz képest, akkor meg azt mondhatjuk, hogy a kooperáció nem is annyira a harmóniához, hanem inkább a viszályhoz áll közelebb. A kooperációban lényege tehát az, hogy egyszerre találhatjuk meg benne a harmóniát (kölcsönös érdekegyezést) és a – potenciális – viszályt (érdekkonfliktust). A fogalmi tisztaságot jelentős mértékben nehezíti az, hogy sokan és sokszor az egoizmus és az altruizmus úgy kezelik, mint egymással teljesen szembenálló fogalmakat, holott a társas preferenciák nyolcas tagolású felosztása egyértelműen mutatja, hogy ez az értelmezés leszűkítő jellegű, és az altruizmus és egoizmus tengelyen ábrázolni kell a pozitív és negatív polaritást egyaránt, hogy teljesebb képet kaphassunk. Ekkor viszont nagyon összezavarhatja a gondolkodást, ha nem helyezzük el pontosan ezen a két tengelyen, hogy hol tudjuk értelmezni, helyén kezelni az olyan fogalmakat, mint előny, haszon, elmaradt kár, hátrány, kár, elmaradt haszon, indokolt és indikolatlan költség, ártalom, veszteség. A játékelméleti fejezeten belül az indirekt reciprocitásról szóló részben (☜) például a kooperáció fogalmánank még a megszokott értelmezést tulajdonítjuk (kooperáció = segítés a másiknak (Egonak költség/hátrány, Alternek előny), ám a versengés, dezertálás tartalmát némiképp átértelmezzük, amikor az "nem segítésként" fogjuk fel (Egonak nincs költség/hátrány, Alternek nincs előny). A játékelméletben a versengés egoista motivációkon alapuló viselkedésnek minősítik, amellyel Ego a saját javát növeli, miközben az Alter számára kárt okoz. Ez a beállítódás annyiban közös a kooperációval, hogy van benne egoista összetevő, viszont annyiban szemben áll a két kategória egymással, hogy a versengésben van valamennyi agresszív motívum, akkor ugyanis az Ego úgy cselekszik, ami az Alter számára hátrányokkal jár. Amikor tehát szembeállítják egymással a két kategóriát, akkor a bennük levő, eltérő polaritású másikra irányultság alapján különböztetik meg őket. Ebben a beállításban eltűnik a köztük levő hasonlóság. Pedig érdemes lenne figyelni arra is. Mivel a játékelméleten belül szinte kizárólag a kooperáció vs. versengés kettőséget alkalmazzák, nem szokás megkülönböztetni az Alterrel szembeni agresszivitás különböző típusait. Ezért van az, hogy a versengés és a destrukció jelenségei egybemosódnak a játékelmélet platformján. Pedig a társas preferenciák nyolcas felosztása azt mutatja, hogy értelmes is, szükséges is lenne ez a megkülönböztetés. Ennek hiányában a versengés fogalma hol az egoista, hol az agresszív (altruizmust nélkülöző) beállítódással válik eggyé.A kooperáció biológiai mechanizmusai
A társadalmi kapcsolatokon belül a kooperációt kialakító és fenntartó mechanizmusokkal sokat foglalkozom majd a könyv játékelméleti fejezetében (☜) A játékelméleti apparátust a biológiai tudományok képviselői is hamar használni kezdték, részben az állatvilágban megfigyelhető kooperációs jelenségek modellezésére. A biológiai modellek eredményeinek bemutatását beilleszthetném a játékelméletet tárgyaló fejezetbe is, de ezt inkább itt teszem meg. Röviden bemutatom a biológiai elemzésekben leírt legfontosabb kooperációs modelleket. Alaposabb elemzésbe nem tudok, nem is akarok belekezdeni, csak egy rövid kitekintésre vállalkozom (a rokoni altruizmus, a reciprok altruizmus, a zöld szakáll hatás, az rosszindulat/spite, a csoportszelekció és a költséges jelzés vagy hátrány-elv fogalmakkal jelölhető eredményeket próbálom meg vázlatosan bemutatni.) A biológusok közül William Donald Hamilton tette meg az első komoly lépést azzal, hogy a rokonok közt létező altruizmus jelenségét megmagyarázta a rokoni altruizmus fogalmára alapozott elméletével Hamilton [hamil] [hamil] Ennek lényege röviden annyi, hogy azok a gének lehetnek sikeresebbek, amelyek olyan viselkedési mintákat örökítenek tovább a szülő gazdaállatokban, amelyek az utódok támogatását biztosítják. Ennek a sikerességének az az egyszerű evolúciós magyarázata, hogy az utódok megsegítésével a szülőállatban levő gén – egyre csökkenő valószínűséggel ugyan, de valamilyen mértékben – továbbél a leszármazottakban is, így az ő fennmaradásuk ugyanúgy a gén replikációját, továbbélését szolgálja. [♦] Az evolúcióbiológián belül a gének által meghatározott kooperatív, altruista jelenségek magyarázataban legtöbbször a Hamilton szabályt alkalmazzák [hamil] [hamil] Ez a szabály két ágens várható költsége és nyereménye közti kapcsolatot írja a köztük levő rokonsági fok erőssége szerint. A fokális ágens az, aki cselekvő szerepben van (akit neveznek Donornak is), a Recipiens pedig a potenciálisan kedvezményezett ágens, aki arra számíthat a kapcsolatban, hogy altruista, kooperatív beállítódással fognak hozzá viszonyulni. A kérdés mindig az lesz, hogy a cselekvő ágens cselekvése, ami mindig költséggel jár számára, milyen eredményeket képes kiváltani a Recipiens számára. A Donor költségét c-vel, a Recipiens előnyét b-vel, a köztük levő rokonsági fokot pedig r-rel jelölve a Hamilton szabály a következő formulával írható le. A képletet értelmezve látható, hogy ha adottnak vesszük a b előny és c költség nagyságát, akkor egy bizonyos rokonsági fok felett az egyenlőtlenség teljesülhet, vagyis a a c költséggel járó, b nagyságú segítséget csak valamely r rokoni szint fölött levő másiknak adja meg az ágens. De a képlet úgy is értelmezhető, hogy ha adottnak veszünk egy rokonsági fokot és egy előnyt a recipiens oldalán, akkor a cselekvő ágens csak egy adott c költségig hajlandó elmenni a recipiens megsegítése érdekében. Az altruizmus, a kooperáció biológiai modellezésében a következő lépés a reciprok altruizmus fogalmával leírható jelenségek elemzése következett az 1970-es évektől kezdve. A kiindulópontot Robert L. Trivers 1971-es tanulmánya jelentette [Trive] A reciprok altruizmus a kooperatív viselkedés egyik fajtájaként értelmezhető és a kölcsönös előnyök cseréjén alapul. Nemcsak azonos fajba tartozó állatok között jöhet létre, és a tartalmát tekintve nagyon sokféle tevékenységre kiterjedhet. A reciprok altruizmus fogalmával megragadható jelenségekre idővel egyre inkább használni kezdték a direkt reciprocitás fogalmát is. Trivers tanulmányában felsorolt néhány fontosabb tevékenységterületet, ahol megjelenhet a reciprok altruizmus (direkt reciprocitás).
"1. Segítségnyújtás veszély esetén (pl. baleset, ragadozók, fajon belüli agresszió)
2. Élelem megosztása
3. A beteg, a sebesült, a nagyon fiatal és az öreg megsegítése
4. A szerszámok megosztása
5. A tudás átadása"
[Trive]
"Az önzés legyőzi az altruizmust egy csoporton belül, de a az altruista csoportok legyőzik az önző csoportokat." [Edwar]
Az evolúcióbiológia egyik nagy alakja, Martin A. Nowak kutatótársaival 2010-ben felvetette, hogy a rokoni altruizmus (kin selection), az inkluzív fitnesz hamiltoni magyarázósémája helyett lehetséges eredeti evolúciós magyarázatot adni, vagyis fölösleges az inkluzív fitnesz elmélet. A javasolt új elmélet közpépontjában a "eusociality" fogalma áll [Marti] Szélesebb kontextusban nem lenne megengedhető, de a biológiai keretek között a rosszindulat vagy a károkozás (spite) fogalmát összevonhatjuk az agresszió fogalmával. Ez utóbbi kategóriát külön tárgyalom (☜) itt csak azt mutatom meg, hogy milyen elméletek születtek a rosszindulat és a kooperáció közti kapcsolatra vonatkozóan. Első pillanatra talán meglepő állítás, de a kooperáció kialakulását bizonyos feltételek mellett meg lehet magyarázni a rosszindulatú, agresszív hozzáállás feltételezésével is [Keith] [Frank] Egy háromszereplős helyzetet feltételezve modellezni lehet a kooperációt a rosszindulatú magatartás jelenlétével. Ekkor a modellbe fel kell venni harmadik szereplőként a másodlagos Recipienst, akinek előnyös lehet, ha a Donor árt a Recipiensnek. Azért lehet előnyös, mert a másodlagos Recipiens helyzete javulhat azzal, hogy kisebb lesz a versenyképessége a Recipiensnek. Ezt a jövőbeni versenyképesség-növekedést egyébként ki lehet terjeszteni akár a Donorra is [WestS] A kooperáció olyan egyedek között is kialakulhat és fennmaradhat, akik nincsenek szoros rokoni kapcsolatban egymással. A csoportszelekció, illetve a hozzá kapcsolható zöldszakáll hatás (greenbeard) fogalmával írják le ezt a jelenséget [Richa] [WestS] Ha nem rokoni kapcsolatban álló egyedek között megjelenik egy beazonosításra (és ezzel persze elkülönítésre) alkalmas biológiai jegy, akkor a jegyet hordozók között megjelenhet és tartósan megmaradhat egymás segítésének szándéka. A 'zöldszakáll' megnevezés Richard Dawkins egyik könyvéből ered, és egy olyan feltűnő jegyre utal, ami ha megjelenik egy populáción belüli kisebb csoport tagjai között, akkor a körön belüliek (tehát a zöld szakállal rendelkezők) el tudják különíteni magukat a többiektől, és egymást támogatva ki tudják használni a kooperáció adta előnyöket. E mechanizmus sikerességéhez tehát csak annyi szükséges, hogy olyan gén(ek) jelenjen(ek) és terjedjen(ek) el az egyedek valamely csoportjában, amely(ek) egyszerre ösztönöz(nek) a kooperációra egyfelől, illetve produkál(nak) látványos csoportazonosító jegyet az egyedekben másfelől. Az azonosító jelek (zöld szakáll) és a segítségre való hajlam kialakulása persze elszakadhat egymástól, vagyis megjelenhetnek azok a csaló egyedek, akik csak a csoportba tartozás külső jegyét hordozzák magukon, és ezzel élvezik a többiek altruista hozzáállását, de maguk nem vállalják a költségeket vagyis nem kooperálnak. Ez a lehetőség a kooperáció fennmaradását nehezíti ugyan, de kiderült, hogy ilyen esetekben is képesek tartósan megmaradni az "altruista zöldszakállak", sőt a kutatók találtak olyan csoportszelekciós mechanizmusokat is, amelyek a károkozással összefonódva fejlődtek ki és voltak képesek a kooperáció terjesztésére [WestS] A költséges jelzés (costly signaling) vagy hátrány-elv (handicap principle) elmélet alapjait Amotz Zahavi teremtette meg [Zahav] [♦] Zahavi a handikepelméletét részben a rokoni altruizmus és a reciprocitáselméletek hiányosságainak pótlására dolgozta ki, amit egyik tanulmánya címével is kifejezett: "Az altruizmus mint hátrány – a rokoni kiválasztás és a reciprocitás [elméletek] korlátai" [Amotz] [♦] A költséges jelzés vagy hátrány-elv elmélet lényegét akkor érthetjük meg igazán, ha arra a helyzetre gondolunk, amire vonatkozóan Zahavi felépítette elméletét (még akkor is, ha azóta a költséges jelzés elméletet más területekre vonatkozóan is alkalmazhatónak ítélték, ítélik). A párválasztás előtt álló egyedek számára érdemes lehet minél feltűnőbb külső jegyekkel felhívni magukra a potenciális partnereik figyelmét. Ezek a jelzések, amelyek minél feltűnőbbek (nagyobbak, színesebbek, hosszabbak stb.), annál inkább jelezhetik az egyed nagyságát, erősségét, rátermettségét, vagyis annál inkább felkelthetik a többiek figyelmét, és ezzel növelhetik a párosodás(ra való kiválsztódás) esélyét. De ha ez így van, akkor érdeke lehet minden egyednek csalnia e téren, és ekkor a jelzést adó minőség (a farok, az agyar, a sörény, a taréj, a tollak nagysága, színe stb.) nem feltétlen lesz összhangban az egyed valódi genetikai értékességével. Ezt a "csalást" úgy akadályozhatja meg az evolúció, hogy a jelzést költségessé tesz. Csak az a jelzés lesz hiteles, megbízható, amelynek "kifejlesztése", fenntartása sokba kerül az egyednek, ami sok esetben abban is megnyilvánul(hat), hogy hátrányt okoz hordozójának. A nagyobb szarvasagancs nehezebb, könnyebben beleakadhat a növényzetbe, nehezebben lehet közlekedni vele a fák között. De az az állat, amelyik képes fenntartani a költséges jelzésre szolgáló vonásait, testrészeit, amelyik viselni tudja a hátrányok következményeit, az méltó a kiválasztásra. És ebben van egy – a szaporodás érdekét szolgáló – jelenbeli önfeladás, altruizmus, amit abban az értelemben nevezhetünk kooperációnak, hogy nem csal saját biológiai jegyeinek "kommunikálásakor". A kooperáció (altruizmus) biológiai mechanizmusainak rövid bemutatását egy áttekintő ábrával zárom. Stuart A. West, Claire El Mouden és Andy Gardner a kooperáció jelenségének gyakori félreértelmezési hibáit számba véve, és ezáltal a kooperáció biológai mechanizmusait is sorban bemutatva az alábbi ábrában összegezték a kooperáció kialakulásának lehetőségeit [West_]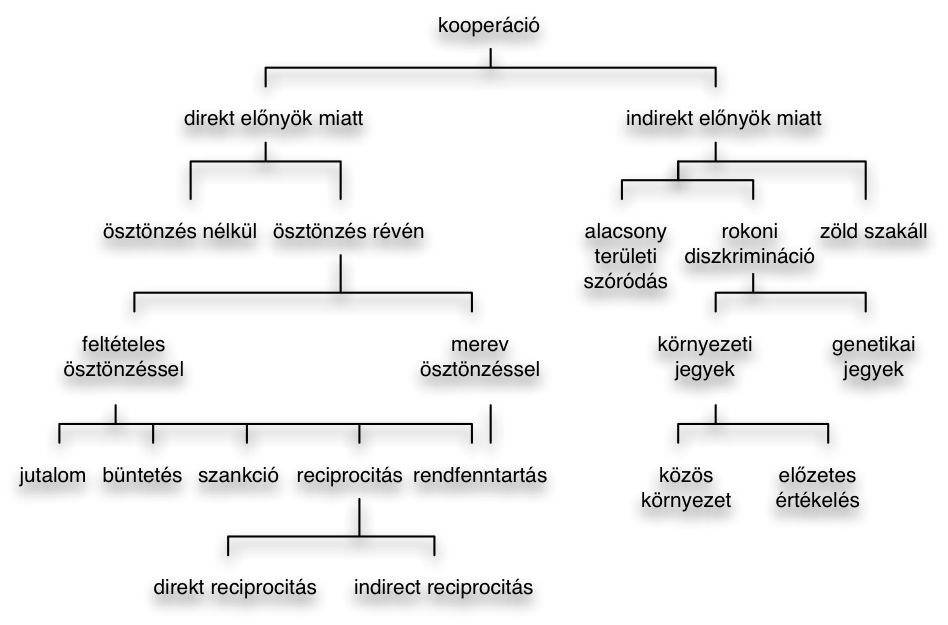
Az ábrán szerepelnek olyan jelenségek is, amelyekről itt nem beszéltem, így vannak megmagyarázatlan fogalmak, de nem gondolom, hogy itt be kellene mutatnom az összes jelenséget. Inkább csak egy jelzést akartam adni arra, hogy az olyan, az emberi társadalmakban fontos jelenségek, mint az altruizmus vagy a kooperáció, hogyan modellezhetők az evolúcióbiológia eszközeivel.
Agresszió
A tudományos vizsgálatok sokáig ugyanúgy, sőt, talán még inkább elhanyagolták a rosszindulatú, károkozásra törő cselekvések jelenségét, mint tették ezt az altruista cselekvések esetében. [♦] Pedig más (például vallási, erkölcsi, művészeti) diskurzusokban mindig is jelen volt a rosszindulat, az agresszió, a gonoszság kérdésköre (akárcsak az altruizmusé). A tudományos magyarázatok hosszabb időn keresztül az egoizmus kizárólagosságára támaszkodtak, és idő kellett ahhoz, hogy a kutatók előbb beemeljék az altruista motívumokat a társadalmi cselekvést leíró modelljeikbe. Még többet kellett várni a rosszindulat jelenségének tudományos vizsgálatára. W.D. Hamilton tágította ki először az elemzési fókuszt, amikor vizsgálandónak tartotta a rosszindulat vagy károkozás (spite) jelenségét az állatvilágban [Hamil] [♦] Hamilton rövid cikke elején még azt a kérdést tette fel, vajon lehetséges-e, hogy egy állat kárt okozzon magának úgy, hogy eközben egy másiknak még nagyobb kára keletkezzék, és ha ez előfordul, akkor ezt hogyan lehetne modellezni. Hamilton a kérdésbe foglalt állítást nevezte el rosszindulatnak. Később azonban, írása egy másik pontján már kicsit másként határozta meg ugyanezt a fogalmat, amikor azt állította, hogy "rosszindulatú az a viselkedés, amely kárt okoz másokat, de nem jár előnnyel az egyén számára". A felállított modell szempontjából végülis az utóbbi értelmezés volt a fontos, a modell eredménye pedig az lett, hogy az átlagos rokonsági szint alatti egyedekkel szemben evolúciós szempontból olykor előnyös lehet a rosszindulatú magatartás. Hogy miként lehet pontosan meghatározni az átlagos rokonsági szint alatti kapcsolatot, az most számunkra nem fontos (a lényeg, hogy a biológusok meg tudják határozni), nekünk csak azért fontos ez a minősítés, mert ezzel lehet "elérni" azt, hogy a Hamilton szabály (☜) képletében a rokonsági fokot jelző r tényező értéke lehessen negatív. Ebben az esetben már értelmezni lehet formálisan is a károkozás jelenségét is, mert így már elképzelhető olyan helyzet, amikor az egyenlőtlenség teljesül, ha a károkozás eredményeként előálló b előny negatívba vált [Gardn] Rosszindulattal kapcsolatos jelenségeket figyeltek már meg az állatvilágban, bár nem túl sokat, és mindig csak fajok közti viszonylatokban. Hamilton maga is azt állítja saját modelljéről, hogy az alapján a rosszindulatú magatartás megjelenését csak ritkán lehet elvárni, mert egyrészt minden rosszindulatú tevékenység költségekkel jár, másrészt nehezen lehet felismerni az átlagos rokonsági szinthez viszonyított "távolságot", harmadrészt a modell olyan, hogy relatíve kis méretű populációk esetében "teszi lehetővé" a rosszindulat megjelenését és elterjedését, ami viszont könnyen a populáció gyors kihalásához is vezethet. [♦] Az állatok közti konfliktusokat korlátozott háborúként értelmezve John Maynard Smith és G.R. Price megpróbálta tipizálni azokat, és elkülönített egymástól több stratégiát (az egér, a héja, a bika/szájhős, a megtorló és a szondázva megtorló stratégiákat), de ezeket itt nem mutatom be [Mayna] Edward O. Wilson szociálbiológiáról szóló könyvében – példákat is mutatva rájuk – hosszabban ír a károkozás és az agresszió jelenségéről [Wilso] és vannak kutatók, akik a károkozás segítségével próbálják meg modellezni az indirekt reciprocitás kialakulását [Johns] Az, hogy az állatvilág vizsgálata során kevesebb figyelmet szenteltek a károkozás, az agresszió jelenségének, sokkal inkább érthetőnek tűnik, mint az a tény, hogy milyen kevés elemzés irányult az emberi agresszió jelenségére (ez alól csak a pszichológia szakterülete jelent kivételt). Természetesen vannak nagyon jó elemzések az agresszivitás jelenségéről [Ramir] [McEll] Az agresszió fogalmára szerkezetét tekintve nagyjából az altruizmus definíciójához hasonló meghatározást adnak a kutatók. [♦]"Agresszióként definiálhatunk minden cselekvést, amely egy másik emberrel szemben ártó szándékkal valósul meg, és az elkövető abban a tudatban van, hogy egyfelől kárt fog okozni a másiknak, másfelől a célszemély igyekszik majd kikerülni ezt a viselkedést." [Bushm]
A definíció fontos eleme, hogy nem elég csak a károkozás tényét megállapítani, a szándékot, tudatosságot is hozzá kell rendelnünk. Ennek hiányában például az orvosi tevékenység egy részét is agressziónak kéne tartanunk. A fogorvos ugyanis fájdalmat okoz a páciensének a gyökérkezelés során, de mivel – tegyük fel, hisz ez a tipikus – nem ez a szándéka, ezért nem minősíthetjük agressziónak. Ebben az értelemben a szadomazo kapcsolatban sincs agresszió, mert az "áldozat" szerepében játszó fél nem akarja elkerülni a fájdalmat. Az agresszióval sokszor együtt jár(hat) a harag érzelme, és ilyenkor indulati-érzelmi cselekvésként kell minősítenünk, de nincs szükségszerű kapcsolat a két jelenség között. Elképzelhető, hogy valaki puszta számításból, hideg fejjel okoz kárt, fájdalmat, sérelmet valakinek. Az agresszivitás jelentkezhet kín- vagy fájdalomokozás formájában, nagyobb károk esetén már szadizmusról beszélhetünk, ami megnyilvánulhat mások megalázásában, fenyegetésében, tényleges fizikai vagy verbális bántalmazásában. Hogy miért cselekszik agresszívan valaki, az nem tartozik e fejezet tárgyához. A biológusok válasza "üss vagy fuss" ("fight or flight") szellemes ugyan, talán még szemléletes is, de az ember motivációs rendszerét azért tarthatjuk ennél bonyolultabbaknak. Alfred Adler volt az, aki az ember legfőbb mozgatórugójaként a hatalmi törekvéseket tette meg, ami a mások fölé kerekedés és a mások fölötti uralkodás vágyától egészen a mások leigázásának, totális maga alá rendelésének vágyáig húzódhat [Alfre] Az adleri emberképben nyilván helye van az agresszivitás, károkozás fogalmának, de azt a kérdést, hogy vajon ez a motívum tekinthető-e a leginkább meghatározónak az ember lelki háztartásában vagy sem, nem nekünk és nem is itt kell megválaszolnunk. A büntetéshez kapcsolódó agresszivitást (károkozást) az ember nagyon fontos részének érzem, amihez képest úgy érzem, hogy a megérdemeltnél kevesebb figyelemet kapott eddig ez a jelenség, de a társas motivációk teljes rendszerén belüli helyét, súlyát nem tudom pontosan meghatározni. A játékelméleti, közgazdasági gondolkodás világába is bekerült a rosszindulatú viselkedés problémája, igaz nem önmagában, hanem inkább a jóindulatú cselekvésekkel való viszonyában. David K. Levine empirikus kísérletekben vizsgálta az altruizmus és rosszindulat jelenlétét [David] Jack Hirshleifer pedig fogalmi szinten elemezte a gonoszság, a másik kárára irányuló motiváció, a jóindulat, illetve rosszindulat (benevolence vs. malevolence) kérdését, és megállapította, hogy a közgazdaságtannak sokkal többet kellene foglalkoznia ez e fogalmak terjedelme alá tartozó jelenségekkel [JackH] Meg kell még jegyeznem azt is, hogy az agresszió színtiszta formájában ugyanúgy csak egy elméleti konstrukció, mint ahogy a tiszta altruizmus kategóriája. Amit már elmondtam egyszer az altruizmusra vonatkozóan, azt ebben az esetben is pontosan ugyanúgy el lehetne mondani. A másiknak való károkozás ugyanis nehezen képzelhető el valamifajta költség vagy haszon nélkül.Autoagresszió
Az autóagresszió, az ágens sajátmaga ellen irányuló rosszindulata a tiszta egoizmus poláris ellentéte. Ekkor (akárcsak az egoizmus esetében) a tudatban csak az Ego van jelen, Alter nem jelenik meg, tehát ilyenkor minden rossz, ártó szándék az Egora irányul. Vannak, akik éppen ezért nevezik ezt mazochizmusnak. Kevés igazi példát lehet erre a jelenségre hozni. Ez nyilván nem véletlen. Az élet, az evolúció, az ember lényegével ellentétesnek tűnik, hogy egy ágens úgy okozzon kárt önmagának, hogy eközben senki, semmi más javát nem szolgálja. Amilyen természetesnek tűnik az "öncélú" – egyéni vagy csoportos – egoizmus, annyira temészetellenes az autoagresszió lehetősége. Az önmagára irányuló agresszió, károkozás legnyilvánvalóbb példái az öngyilkosság, öncsonkolás, önbüntetés különböző formái lehetnek, de ezek túlnyomórésze inkább az önfeláldozás fogalma alá sorolható be inkább. Az önbüntetés azon példái tartozhatnak ide, amelyekben nem találunk semmiféle olyan motívumot, amelyben a más – egyéni vagy csoportos – ágens is feltűnne. Nem nagyon hiszem, hogy az állatvilágból lehetne erre példát találni, de az ember esetében ezt el tudom képzelni. De azért ritka jelenségnek kell tartanunk.Önfeláldozás
Az önfeláldozásról akkor beszélünk, ha a cselekvő magának kárt, költséget, a másiknak előnyöket okoz. A tiszta altruizmus esetén Ego, a cselekvő ágens nem foglalkozik sajátmagával, csak a másik ágensre, Alterre figyel. Ha az altruizmust a "másiknak kedvezés" jelenségeként értelmezzük, akkor az önfeláldozás jelenti a legerősebb altruizmust. A játékelmélet világából több olyan helyzetet azonosíthatunk, amely az önfeláldozás példájaként minősíthető, bár sajnos abban a világban terminológiai szempontból elég nagy fogalmi pongyolaságot találhatunk. Az aszimmetrikus játékok közül az 'anya-fia bankrabló' nevű játék mindenképpen az önfeláldotás jelenségébe sorolható [syiDi] Nem érzem feladatomnak, hogy kitérjek itt az emberi öngyilkosság kérdésére, de annyit nyilván érdemes megemlítenem, hogy Durkheim az öngyilkosság típusai közé beveszi az altuista öngyilkosság fogalmát, amit úgy jellemez, hogy erős társadalmi integráció létezésekor a közösség elvárása olyan erős az egyénnel szemben, hogy utóbbi maga megteszi az önfeláldozó lépést [Emile] Az viszont egyáltalán nem igaz, hogy az öngyilkosság kizárólag emberi sajátosság volna. Bár nem túl gyakori, de előfordul az állatvilágon belül [Thoma] A kutatók adaptív öngyilkoságnak nevezik, és a létezését úgy magyarázzák, hogy az egyed a saját génjének sikeres továbbörökítése érdekében pusztítja el magát. Megeshet, hogy a borsótetű (Acyrthosiphon pisum) testébe darazsak beszúrják a tojásaikat, hogy az utódaik parazitaként nevelkedjenek fel a borsótetű testéből táplálkozva. Ilyen esetekben előpordul, hogy az így megfertőzött borsótetű ledobja magát a levélről, ahol addig a társaival együtt élt. A földön biztosan áldozatává válik bogaraknak, de önfeláldozásával saját génjeit hordozó rokonai számára előnyöket biztosít, mert a parazita darázslárvák nem vándorolhatnak tovább a társaira. Az ausztráliai vöröshátú pók (Latrodectus hasseltii) nősténye is megeszi a hím párját, de ezt a kutatók nem a nőstény agresszivitásával, hanem a hím önfeláldozásával magyarázzák [Thoma] Az önfeláldozásnak ugyanis adaptív előnye van, mert a magát halálba kopuláló hím saját génjeit továbbörökíti, míg a halálos párzástól megmenekülő hímtársai erre nem képesek – mindaddig, amíg nem vállalkoznak saját halálos kalandjukra. Ha figyelembe vesszük Oldenquist csoportegoizmus fogalmát (☜) akkor ezt a biológiai jelenséget úgy értelmezhetjük, hogy az az öntudat nélküli altruizmus fogalmával írható le. A vallási áldozat, az emberáldozat, a katonai önfeláldozás (Dugonics Titusz) sok-sok példája is idetartozik, mert ezek olyan önkárokozások, amelyekben mindig megtalálható valamilyen általánosított másik, valamilyen csoport, szuperindividuum.Destrukció
A romantikus emberfelfogás a destrukciót [♦] károsnak, elítélendőnek, és ezzel együtt azonban (és talán éppen ezért) ritka jelenségnek tekinti. Első ránézésre úgy tűnhet, hogy még elméletileg is alá lehet ezt támasztani, hiszen a destrukció mindkét fél számára, tehát Egonak is, Alternek is kárt, hátrányt okoz, és nehéznek tűnik érveket szállítani a kettős hátrányokozás értelmére. Pedig nem így van. Mielőtt az okokról és mechanizmusokról beszélnék, előbb hivatkoznék arra, hogy a romantizicmustól mentes közgondolkodás is "tisztában van" azzal, hogy a mindennapi életünkben is van destrukció. Ezt bizonyítja a következő mondás: "A szellem kiszabadul a palackból, és azt mondja a parasztnak, hogy egyet kívánhat, de akármit is kíván, a szomszédja kétszer annyit fog kapni. – Szúrd ki az egyik szemem! – jön a válasz." A tanmese tartalmát még rövidebben kifejezi a dögöljön meg a szomszéd tehene is – az előbbinél jóval gyakoribb – mondásunk. Szóval igenis van destrukció az életünkben. A kérdés az, hogy milyen "érvek", milyen indokok, milyen mechanizmusok képesek kiváltani ezt a jelenséget. Legalább két érvet, két mechanizmust meg tudok nevezni. Egyfelől az érzelmi mozgásaink miatt kerülhetünk ilyen helyeztebe, amikor valamilyen frusztrációt az indulati-érzelmi mechanizmusaink a destrukción keresztül tudnak csak megoldani. A "dögöljön meg a szomszéd tehene is" felkiáltás mögé könnyen ellképzelhetjük azt a helyzetet, amelyben az elkeseredettség úgy vakítja el az embert, hogy csak egyfajta totális romboláson keresztül látja feloldhatónak belső feszültségeit. Ha jobban belegondolunk, akkor már az indulati-érzelmi döntések mögött is ott dolgozik bennünk valamifajta belső büntetési szándék, és ezt, mármint a büntetés jelenségének hatókörét kiterjeszthetjük. Ha így teszünk, akkor felismerhetjük, hogy érzelmileg kevésbé meghatározott helyzetekben is tetten érhetjük a büntetésen keresztül megvalósított destrukciót. Az alkujátékok elemzése során kiderül (☜) hogy bizonyos játékhelyzetekben (például az ultimátumjátékokban) az emberek gyakran olyan döntéseket hoznak, amelyekkel mind magukat, mind a társukat elütik a várható nyereségtől, tehát destrukciót hajtanak végre. Ennek magyarázata pedig egyszerűen az, hogy a felajnálott nyeremények kölcsönösen káros visszautasítását a méltánytalannak tekintett ajánlatokkal szembeni megtorlásként értelmezhetjük [all:m] Amennyiben ez az értelmezésem helytálló, akkor viszont az állatvilágban, ahol a magasabbrendű cselekvésként értelmezhető büntetés jelenségét nem feltételezhetjük, nem számolhatunk a destrukció jelenségére sem. Ellenben amilyen mértékben "szétterül" az emberi társadalmakban a büntetés intézménye, olyan kiterjedt mértékben kell megtalálnunk a destrukció jelenségét is. A büntetést és nyilván a mélyében meghúzódó destrukciót azért nehéz egyértelműen értékelni, mert a benne rejtőző paradoxon kettős természetűvé teszi (☜)Méltányosság, szolidaritás, reciprocitás
A bemutatott társas preferenciák a fogalmi építkezés alapfogalmai közé tartoznak, amelyek persze felbukkanhatnak összetett fogalmak komponenseiként. Vannak gyakran elemzett fogalmak, amelyeket a társadalmi kapcsolat kategóriája alá kell besorolnunk, de már összetett fogalmaknak kell tartanunk őket. Ilyen a reciprocitás fogalma annak minden altípusával együtt, ilyen a méltányosság vagy igazságos (fair) beállítódás vagy cselekvés kategóriája, és ilyen a szolidaritás, a másokkal való együttérzés fogalma is. Ezek mindegyikéről tengernyi kutatás, elemzés, tanulmány, könyv született, melyek bemutatása meghaladja a lehetőségeimet. A reciprocitás fogalmát máshol már bemutattam [syiDi] itt csak néhány fontos vonását akarom kiemelni. A reciprocitás mint időben eltolt viszonzások rendszere sokrétű fogalom, és ezért nem meglepő, hogy sokféleképpen próbálták meg tipizálni. Számomra kétféle szempont szerinti felosztás fontos, amelyek azonban nem ortogonálisak egymásra, van átfedés közöttük. Szokás pozitív és negatív reciprocitás, illetve direkt és indirekt reciprocitásról beszélni. Fehr és Gächter a pozitív és a negatív reciprocitást aszerint különbözteti meg, hogy valaki kooperál, jutalmaz vagy dezertál, büntet [fehr:] Herbert Gintis ugyanerre a kettősségre a gyenge, illetve erős reciprocitás fogalmakat alkalmazza [Ginti] Az altruizmus és reciprocitás kapcsolatát elemzi még Gintis társaival az 'Explaining altruistic behavior in humans' című cikkében [ginti] amelyből kiderül, hogy a kutatók között abban a tekintetben nincs vita, hogy a pozitív és negatív reciprocitás fogalmát a jutalmazó, kooperatív, illetve a büntető viselkedéshez kötik. Ez a szembeállítás persze korántsem újkeletű. Még jóval a játékelmélet, a kísérleti közgazdaságtan "megjelenése" előtt a szociológus Alvin W. Gouldner [gould] vagy az antropológus Marshall Sahlins [sahli] is hasonló felosztást javasoltak. A könyv játékelméleti részében külön fejezetet szentelek a direkt (☜) és indirekt reciprocitás (☜) fogalmainak, ezért itt nem térek ki rájuk. A különbség annyi köztük, hogy a viszonzás egymást ismerő vagy ismeretlen emberek között valósul-e meg. Egy rövidebb részben kitérek a méltányosságelméletekhez köthető alkujátékok kérdésére is, de ennek a kérdéskörnek lényegesen kevesebb figyelmet szentelek. Egyáltalán nem foglalkozom viszont a szolidaritás problémakörével. Nem azért, mert nem tartom fontosnak, inkább a kellő felkészültség hiányzik. Magyar nyelven a méltányosságelméletekről jó áttekintést adnak Gulyás Attila cikkei [gulya] [Gulya] a szolidaritás témakörében Janky Béla könyvét ajánlom az érdeklődőknek [Janky]A társadalmi kapcsolat típusai
Az előző fejezetben a beállítódásokkal kapcsolatos fogalmakat elemeztem. Különösen sokat foglalkoztam az ágensre irányultság különböző formáival. A fejezet bevezetőjében két dolgot is jeleztem. Egyfelől azt, hogy ezek a fogalmak mind a társadalmi kapcsolat fogalma alá sorolhatók be, másfelől azt, hogy az ágensre irányultsággal kapcsolatos fogalmak szűkebb terjedelműek a társadalmi kapcsolat fogalmához képest. Természetesen minden generikusan alárendelt fogalom szűkebb terjedelmű a fölöttes kategóriához képest, de itt nem erre a trivialitásra utalok. Az ágensre irányultság mint beállítódás figyelembe vétele fontos a társadalmi kapcsolat tipizálása szempontjából, de a szükség van valami másra is. Amikor Max Weber meghatározta a társadalmi kapcsolat típusait, akkor két dimenzió mentén különítette el az új kategóriákat. Egyrészt használta azt a dimenziót, amit én az ágensre irányultság fogalmával ragadtam meg, másrészt hivatkozott a társadalmi cselekvések típusaira (racionális, illetve aracionális cselekvések két nagy osztályára), amelyeket korábban én is bemutattam. Mivel nagyon fontos kategóriákat vezetett be ezen a ponton, érdemes megnéznünk, hogyan tette mindezt. A társadalmi kapcsolat meghatározása után Max Weber a fogalom három altípusát különítette el egymástól. Először a harc (konfliktus) fogalmát definiálta, majd kicsivel később pedig megadta a közösség és a társulás meghatározását is.
"Harcnak nevezünk egy társadalmi kapcsolatot, amennyiben a cselekvőt az a szándék vezeti, hogy saját akaratát a másik vagy a többi féllel szemben keresztülvigye."
[weber]
" Közösségnek nevezzük a társadalmi kapcsolatot, ha a társadalmi cselekvést … a résztvevők szubjektíve átérzett (érzelmi-indulati vagy tradicionális) összetartozásán alapuló beállítódás jellemzi."
" ... társulásnak nevezzük a társadalmi kapcsolatot, ha a társadalmi cselekvést racionálisan (érték- vagy célracionálisan) motivált érdekkiegyenlítődésen vagy ugyanígy motivált érdekkapcsolódáson alapuló beállítottság jellemzi."
[weber]
| magára irányuló | másikra irányuló | |||||||||||||
| ? | harc | ? | ||||||||||||
| ? | ? | társulás | ||||||||||||
| ? | ? | közösség | ||||||||||||
| magára irányuló | másikra irányuló | |||||||||||||
| harc | együttműködés | |||||||||||||
| racionális | ellenfél | társulás | ||||||||||||
| aracionális | ellenség | közösség | ||||||||||||
| magára irányuló | másikra irányuló | egyikre sem irányuló | ||||||||||||
| harc | együttműködés | semlegesség | ||||||||||||
| racionális | ellenfél | társulás | kívülálló | |||||||||||
| aracionális | ellenség | közösség | kívülálló | |||||||||||
Interdependens cselekvések
A társadalmi cselekvésről szóló fejezetben eddig azt a kérdést jártam körül, hogy mit jelent a cselekvés fogalma, milyen típusai vannak a cselekvésnek, és kik a társadalmi cselekvések ágensei, az azt megelőző fejezetben pedig foglalkoztam az intencionalitás, az akarat problémájával. A cselekvés fogalmi lényegeként az intencionáltság mozzanatát adtam meg. Eddig azonban az egyéni cselekvőre koncentráltunk, és bár a másikra irányuló társadalmi kapcsolatokban már nyilvánvalóan figyelembe kellett venni a cselekvő, a fokális ágens (Ego) mellett a társadalmiságot kifejező másik résztvevőt (Altert) is, ezekből a fogalmakból, ezekből az elemzésekből még hiányzott egy fontos minőség. Eddig ugyanis még nem figyeltünk arra a lehetőségre, amikor az egyéni cselekvések megvalósulása, azok sikeressége a kapcsolatba került felek mindegyikétől függ, vagyis a felek kölcsönös függőségben vannak egymással. Ezt a társadalmi állapotot kölcsönös függésnek vagy interdependenciának, interdependens helyzeteknek nevezhetjük. A továbbiakban az interdependens helyzetek, és az ilyen helyzetekbe került cselekvések alapvonásait szedem össze. Ha már tisztázva van, hogy:- a cselekvés elméletén belül mit jelent a tevés és a tartózkodás fogalma,
- az intencionalitás elméletén belül mit jelent az akarat fogalma,
- a cselekvés elméletén belül mit jelent az ágens fogalma,
| Alter akarja | Alter nem akarja | |||||||||||||
| Ego akarja | ágens cselekvését | ágens cselekvését | ||||||||||||
| Ego nem akarja | ágens cselekvését | ágens cselekvését | ||||||||||||
| Alter akarja | Alter nem akarja | |||||||||||||
| Ego akarja | Ego megtegye (1) | Ego megtegye (2) | ||||||||||||
| Ego akarja | Ego tartózkodjon (3) | Ego tartózkodjon (4) | ||||||||||||
| Ego akarja | Alter megtegye (5) | Alter megtegye (6) | ||||||||||||
| Ego akarja | Alter tartózkodjon (7) | Alter tartózkodjon (8) | ||||||||||||
| Ego nem akarja | Ego megtegye (9) | Ego megtegye (10) | ||||||||||||
| Ego nem akarja | Ego tartózkodjon (11) | Ego tartózkodjon (12) | ||||||||||||
| Ego nem akarja | Alter megtegye (13) | Alter megtegye (14) | ||||||||||||
| Ego nem akarja | Alter tartózkodjon (15) | Alter tartózkodjon (16) | ||||||||||||
| Alter akarja | Alter nem akarja | Alter akarja | Alter nem akarja | |||||||||||
| Ego akarja | Ego megtegye | Ego megtegye | Alter megtegye | Alter megtegye | ||||||||||
| (1) | (2) | (5) | (6) | |||||||||||
| Ego akarja | Ego tartózkodjon | Ego tartózkodjon | Alter tartózkodjon | Alter tartózkodjon | ||||||||||
| (3) | (4) | (7) | (8) | |||||||||||
| Ego nem akarja | Ego megtegye | Ego megtegye | Alter megtegye | Alter megtegye | ||||||||||
| (9) | (10) | (13) | (14) | |||||||||||
| Ego nem akarja | Ego tartózkodjon | Ego tartózkodjon | Alter tartózkodjon | Alter tartózkodjon | ||||||||||
| (11) | (12) | (15) | (16) | |||||||||||
Hatalom
Amennyire meghatározza életünket a hatalom jelensége, annyira nem tudunk mit kezdeni vele. Nem tudjuk igazán megragadni, nem tudjuk leírni tudományos eszközökkel. Mindenhol ott van, de rejtőzködik, bújkál, letagadja magát. Azok tagadják le leginkább, akik élnek vele, és azok érzik leginkább, akikkel szemben élnek vele. Nem véletlen az a rengeteg értelmezési, definiálási kísérlet, ami a fogalom megragadására irányult. [♦] Nem érthetjük meg igazán a cselekvéseinket, ha nem tudjuk, mit jelent ez a fogalom, ha nem értjük, maga a jelenség hogyan befolyásolja életünket. A sokféle értelmezési kísérlet közül még mindig Max Weber meghatározását tartom a legpontosabbnak, így abból kiindulva próbálom meg explikálni a fogalmat. Nem véletlen, hogy Weber a kategóriatanában rögtön egymás után definiálta a hatalom és az uralom fogalmát, hiszen a két fogalom sok szempontból nagyon közel van egymáshoz, de az sem véletlen, hogy két kategóriát tartott szükségesnek elkülöníteni, nem egy fogalmat definiált. Persze nem könnyű a pontos határvonalat meghúzni a két weberi fogalom között, ez sokaknak nem is sikerült, és nagyon sok félreértés, félreértelmezés született a két fogalom jelentésével, egymáshoz való viszonyával kapcsolatban. Itt egyelőre csak a hatalom fogalmát próbálom meg körbejárni, az uralom kategóriáját máshol elemzem (☜) Az induláshoz idézzük Webert. [weber]"Minden olyan esetben hatalomról beszélünk, ha egy társadalmi kapcsolaton belül van rá esély, hogy valaki saját akaratát az ellenszegülés ellenére is keresztülvigye, függetlenül attól, hogy min alapul ez az esély."
A hatalom fogalmának igazi értelme az uralommal szembeállítva fedhető fel igazán, de erre még várnunk kell. Az viszont rögzíthetjük, hogy a hatalom egymással ütköző akaratok esetén létezik, vagyis az akaratkonfliktust, mégpedig a nyílt akaratkonfliktust szükséges előfeltételként kell értelmeznünk. És akkor beszélhetünk hatalomról, ha ez a konfliktus valamilyen kényszer alkalmazásával oldódik fel. Ezt fejezi ki az "ellenszegülés ellenére is" passzus a weberi definícióban. A hatalomban mindig van egy domináns és egy alárendelt "szerep", mindig van egy, a hatalmat gyakorló és egy, a hatalomgyakorlást elszenvedő fél. Az is nyilvánvaló még a meghatározásból, noha tételesen nincs kimondva, hogy a hatalomgyakorlást elszenvedő fél akarata nem teljesül, hiszen akaratkonfliktus esetén a domináns fél akarata csak akkor érvényesíthető, ha a szembenálló másik akarat nem teljesül. Márpedig az akarattal rendelkező ember (lény) azt nagyon nehezen viseli, ha az akarata ellenére kell valamit megtennie. A szabad akarat kérdése itt a másoktól független, mások által nem blokkolt vagy nem direkt módon befolyásolt akaratképzés lehetőségét jelenti. Szándékosan fogalmaztam ennyire kitekert módon. Nem minden akaratbefolyásolás tartozik a hatalom jelenségébe, csak azok, amelyek a nyílt akaratkonfliktusokat kényszer alkalmazásával törik fel. Az akaratszabadság tehát itt a másoktól független akaratképzés lehetőségét jelenti, és az akarat ilyen értelemben vett szabadsága – úgy tűnik – az egyik legfontosabb emberi minőségünk. [♦] Az akarat szabadságának pozitív értékéből fakad, hogy az akarat megtörése negatív érzelmeket vált ki. A hatalom lényegi összetevőjét jelentő kényszer alkalmazása után mindig észlelhetjük a "szenvedő" fél frusztráltságát, méltánytalanságérzetét. A hatalom pont azért rejtőzködő természetű, mert a tényleges hatalomgyakorlást, azaz mások akaratának megtörését társadalmi szinten elítéljük, és a társadalomban való létezésünk óta ki akarjuk szorítani a békés hétköznapok világából. Ez a tartós társadalmi konszenzus azonban eddig sem tudta, és vélhetőleg a jövőben sem tudja megakadályozni a hatalmon keresztüli befolyásolás jelenségét. Ha a hatalmat olyan jelenségként értelmezzük, amelyben a két ágens közti akaratkonfliktust valamilyen kényszer alkalmazásával oldja fel az egyik fél, akkor ezt a jelenséget megtalálhatjuk az állatvilágban is. Amikor szűkösek az erőforrások, amikor meg kell harcolni az élelemért, a területért, a szállásért, a szexuális partnerért, akkor ez a harc egymással szembenálló állatok között zajlik, ahol legtöbbször a nyers erő dönt. Az alfahímet nem megválasztják a többiek, hanem a legerősebb egyed harcolja ki magának ezt a pozíciót. A csípkedési sorrend nem megállapodás kérdése, nem is az érkezési sorrendet fejezi ki, hanem az aktuális erőviszonyok puszta leképezését jelenti. A szűkös erőforrásokhoz való hozzáférés sorrendjét jelzi mindenki számára, ami persze az időben folyamatosan változik, hiszen az erősek elgyengülnek, a korábbi gyengék erősekké válnak. A sorban elfoglalt pozíciót mindig meg kell védeni, és persze mindig lehet támadást indítani egy jobb helyért. És mindig az erő dönt. Az erőszakalkalmazás a hatalom legelemibb és legősibb forrása. Amikor tehát a hatalom eszközét alkalmazza az ember, akkor az egyik legősibb biológiai késztetést (és technikát) hagyja érvényesülni. Eddig még tételesen nem mondtam ki, de úgy használtam az erőszak fogalmát, mintha a hatalom egyfajta forrásaként értelmeznénk. A szembenálló fél akaratának megtöréséhez mindig szükség van valamilyen kényszerítő eszközre, és ezt az eszközt nevezhetjük a hatalom forrásának. Eddig annyi derült ki, hogy ez lehet az erőszak(alkalmazás). A kérdés az, hogy elképzelhető-e más ilyen eszköz, vagyis létezik-e másfajta hatalomforrás is. A válasz nyilván igenlő. A tudás (információ), a pénz (gazdasági erőforrás), a pozíció (hatáskör) olyan erőforrásként is értelmezhetőek, amelyek egyenlőtlen eloszlása aszimmetrikus viszonyokat teremt a felek között, és a hatalom gyakorlását teszi lehetővé. Az a társadalmi konszenzus, hogy a hatalomgyakorlás nem kívánatos jelenség, amit ki kell szorítani a társadalmi gyakorlatokból, megnyilvánul abban a tényben is, hogy a hatalomgyakorlás minden formáját, vagyis a hatalom mindenféle eszközének, forrásának alkalmazását bünteti a jogrend. Az erőszak, a zsarolás, a pénzzel, gazdasági erőfölénnyel való befolyás, a bennfentes kereskedés, a monopolhelyzettel való visszaélés, a szervezeti pozíció kihasználása, a hatáskörtúllépés, a politikai befolyás tilalma mind valamilyen hatalomgyakorlási helyzetet akar megakadályozni a jog eszközével – miközben a hatalom potenciális forrásait "nevezi meg". A társadalmi választások elmélete rengeteg olyan problémát vetett fel (☜) amelyek a hatalomgyakorlás különböző lehetőségeiként is értelmezhetők egyben. A háború művészete, a hatalommérnökség, a harci konfliktusok feloldásának, megnyerésének technikái is – legalább részben – a hatalom eszközeiről, forrásairól és ezáltal kicsit a hatalom típusairól is szólnak, de ezek tudományos feldolgozása még várat magára. Weber azt írta a hatalom kategóriájáról, hogy amorf fogalom. Részben ez magyarázhatja azt, hogy nagyon kevés értelmes tipizálás jelent meg a hatalom fogalmával kapcsolatban. Talán az egyetlen régóta létező és elfogadható tipizálás azt a kettőséget ragadja meg, hogy az akaratérvényesítés során a hatalmat gyakorló fél mire tudja rávenni a másikat: arra, hogy megtegyen, vagy arra, hogy ne tegyen meg valamit. Ennek megfelelően beszélhetünk pozitív hatalomról, amikor az alárendelt fél megtesz valamit, amit egyébként önszántából nem akarna, illetve negatív hatalomról, amikor az alárendelt egyén nem teszi meg azt, amit egyébként megtenne magától. Bármennyire is száműzni szeretnénk ezt a jelenséget a társadalmi térből, a hatalom mindenhol jelen van, sokszor ez dönti el a konfliktusaink kimenetét. Ez a felismerés könnyen kialakíthatja azt a pesszimista hozzáállást, hogy ez ellen nem lehet semmit sem tenni, mindig minden a hatalmasoké volt a múltban, van a jelenben, és lesz a jövőben, a hatalom mozgatja a világot. Bár én is úgy vélem, hogy a hatalom az egyik legmeghatározóbb tényezője a társadalom működésének, a hatalom mindenhatóságának tézisében nem hiszek. Említettem már, hogy a hatalmat csak az uralomhoz való viszonyában érthetjük meg teljesen. De azt még nem mondtam, hogy van egy másik fontos szempont is, amit figyelembe kell vennünk, ha teljes mélységben meg akarjuk érteni a hatalom fogalmát. Jack Hirshleifer hívta fel a figyelmet arra [JackH] hogy a hatalom nem mindenható. Hirshleifer a katonai konfliktusról értekezett, de érvelését nyugodtan kiterjeszthetjük a hatalomgyakorlás mindenféle formájára. A földrajzilag kicsinek mondható csatatéren a nyertes mindent visz, ami azt jelenti, hogy ha – akárcsak egy picinyke katonai erőfölény birtokában, de – megnyeri a csatát, akkor utána – a katonai erőfölényéhez képest aránytalan mértékben – megszerez mindent magának. A közgazdaságtanban ezt a jelenséget a növekvő mérethozadék vagy skálahozadék (increasing-return) elvével írják le. Ez az elv azonban nem terjeszthető ki a legyőzött ország teljes területére, nem érvényes már a háború egészére nézve sem, nem beszélve a békés időszakokról. Minél nagyobb földrajzi területre szóródnak szét az emberek (a csata után), annál inkább egy másik logika, a csökkenő mérethozadék vagy skálahozadék (decreasing-return) elve kezd érvényessé válni. Ekkor az egyre több katonai/hatalmi erőforrás biztosítása is csak relatíve egyre kevesebb eredményt képes produkálni. Minél inkább szészóródnak az emberek a földrajzi (vagy a társadalmi) térben, annál nehezebben lehet hatalomtechnikákat alkalmazni velük szemben. Hiershleifer megjegyezte még azt is, hogy a növekvő mérethozadék elve miatt lehet kialakítani (és fenntartani) az állami erőszak-monopóliumokat, és a csökkenő mérethozadék logikájából érthető meg, miért nem alakul ki a világállam, vagy miért esnek szét a nagy birodalmak, és miért képtelenek minden téren érvényesíteni a nagy hatalomközpontok saját akarataikat.A hatalom fogalmának explikációja
Korábban bemutattam, hogy milyen interdependens társadalmi kapcsolatba kerülhet két cselekvő (☜) Ezek közül voltak konszenzusos, voltak konfliktusos helyzetek. Definiáltam a harc (konfliktus) fogalmát is (☜) Az akaratkonfliktus lényege, hogy az egymásnak feszülő (egymásnak ellentmondó) akaratok csak egymás kárára valósulhatnak meg. A kérdés tehát az, hogy miként "győzhet" az egyik akarat a másik "fölött", vagy fordítva: miért nem érvényesül valaki saját akarata a másik ágens akarata ellenében. Ezen a ponton nagyon körültekintőnek kell lennünk. A pontos ítéletkezéshez arra van szükség, hogy figyelembe vegyük azt, hogy az éppen vizsgált helyzetben melyik ágens cselekvésével kapcsolatos akaratkonfliktusról van szó. E szempont figyelembe vételével kétféle akarattípust különböztethetünk meg. Beszélhetünk saját cselekvésre irányuló 'cselekedni akarás'-ról, illetve a másik cselekvésére irányuló 'befolyásolni akarás'-ról. Az akaratkonfliktus ténye még csak az ellentétes akaratok létezését fejezi ki, semmi többet. A nagy kérdés az, hogy milyen módon oldódik fel ez a konfliktus. A konfliktus kétféle lehetséges kimenete közül az egyik az, amikor a cselekedni akarás érvényesül (tehát a befolyásolási akarat kudarcot vall), másik az, amikor a befolyásolási akarat érvényesül. Az első esetben a befolyásolási akarat sikertelen marad, a másodikban sikeres. Ha valaki az utcán elém áll, és pénzt követel tőlem, de én nem akarok adni neki, kitérek az útjából, tovább megyek, akkor a másik nem volt képes érvényesíteni az akaratát velem szemben. Ha viszont a másik fél egy fegyvert fog rám, és azzal fenyeget, hogy lelő, akkor odaadom a pénzemet neki, saját – eredeti – akaratom ellenére. Konfliktus esetén mindkét fél elsődleges akarata valamelyikük cselekvésére irányul, de a két akarat eltér egymástól. Az akarat jelzése azonban még nem elég a megvalósuláshoz. A saját akarat érvényesítéséhez szükség van egy második akaratra is, mégpedig arra az akaratra, hogy a másik fél változtassa meg saját elsődleges akaratát, illetve a partnerben olyan másodrendű akarat keletkezik, aminek tartalma; nem akarni a saját elsődleges akaratának megváltoztatását. A konfliktushoz ez a kétfajta és kétszintű akaratkülönbség elengedhetetlen. Lehetséges, hogy valaki az elsődleges akaratkonfliktus konstatálása után inkább visszalép, nem akarja érvényesíteni saját akarát a másikkal szemben. Viszont ha mégis erre törekszik, akkor az akaratok kétszintű konfliktusa feloldásához szükség van valamire. A befolyásoló akarattal rendelkező ágens oldaláról szükség van arra a pótlólagos cselekvésre, aminek eredményeként a cselekedni akaró fél megváltoztatja a saját eredeti akaratát, és a befolyásoló akarat szerint fog cselekedni. A befolyásoló akarattal a kapcsolatba belépő ágensnek elfogadható (gyakorlati) indokot kell szolgáltatnia arra vonatkozóan, hogy a cselekedni akaró (vagy nem akaró) ágensnek miért kellene megváltoztatnia a saját cselekvésére irányuló eredeti akaratát. A befolyásoló akarat kifejtése, kifejezése elsőrendű cselekvés, az megfelelő indok szolgáltatása viszont már másodrendű cselekvés (ami egy másodrendű akarattal kapcsolható össze), hiszen a befolyásolni akaró ágens indokot szolgáltató cselekvése (illetve az erre irányuló akarata) a másik fél elsőrendű cselekvésére irányuló akaratának megváltoztatására irányul. A folyamatot így ábrázolhatjuk.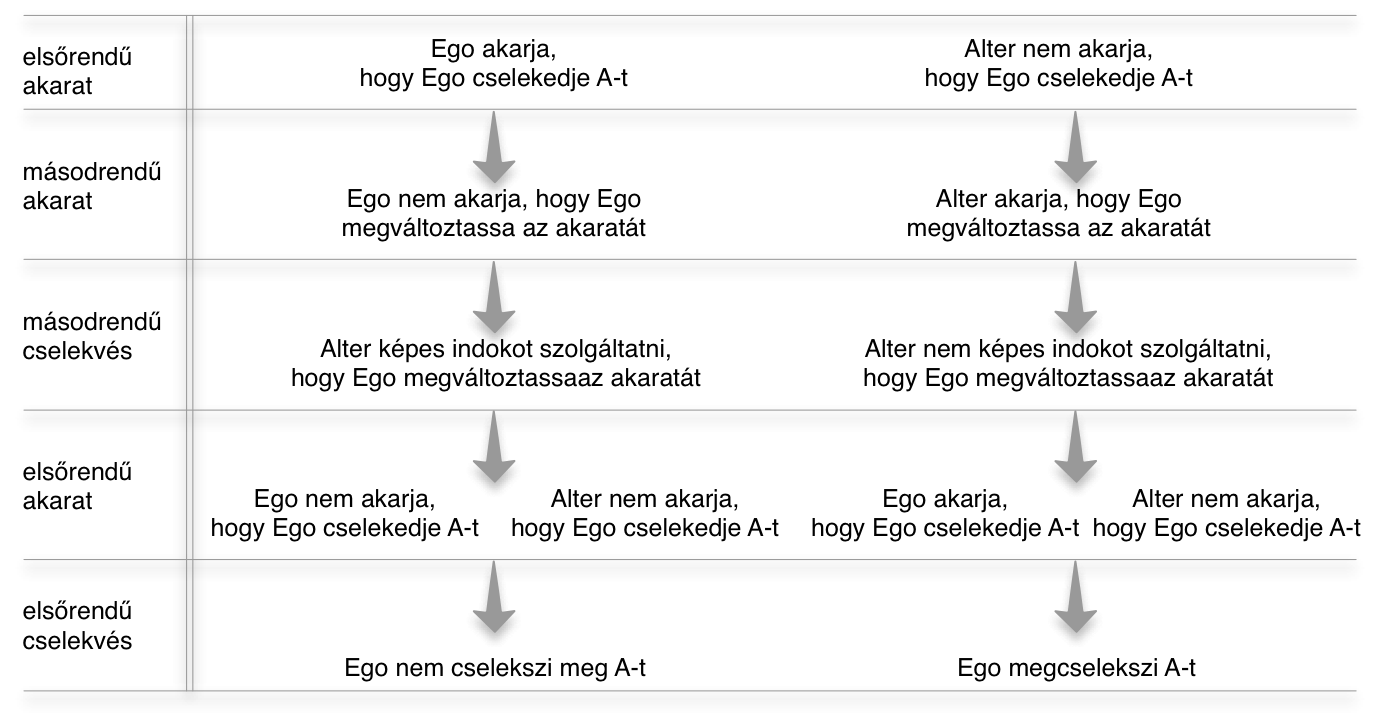
Háromféle módszer, háromféle indok szolgáltatása lehetséges a cselekvő eredeti akaratának megváltoztatására. Az egyik módszer a --- weberi értelemben vett – hatalom (power), a másik a – weberi értelemben vett - uralom (authority) gyakorlása, a harmadik a "vitán keresztüli" meggyőzés (belief-revision). A hatalom esetében az akaratot megtörik ("ellenszegülés ellenére viszik keresztül az akaratot"), az uralom esetében az ellenkezést úgy iktatják ki (☜) hogy egy norma által előírt kötelességre vagy tilalomra hivatkoznak. A vita során érveket hoznak fel egymással szemben a másik akaratának megváltoztatása érdekében. Akkor beszélhetünk hatalom jelenségéről, ha a hatalmat gyakorolni kívánó fél valamilyen kényszert alkalmaz gyakorlati indokként a vele szemben levő akaratának megváltoztatására. Ahogy azt már korábban jeleztem, ez lehet erőszakkal, tudással, pénzzel, gazdasági erőforrással, szervezeti pozícióval, de akár valamilyen a másik személyes elköteleződéssel való (vissza)élés. A lényeg az, hogy az adott társdalmi kapcsolatban alkalmas legyen az alávetett fél akaratának megtörésére. Ha hatalmi helyzeteket akarunk megérteni, akkor mindig azt kell megtalálnunk, hogy milyen hatalomforrásra tudott támaszkodni a hatalmat gyakorló fél, illetve ez miért volt alkalmas arra, hogy az alávetett személy megváltoztassa az akaratát.
Kényszermentes társadalmi kapcsolat
"Két ember megy a szavannában, amikor meglátnak egy oroszlánt. Az egyik elkezdi ledobálni magáról mindenét, hogy gyorsabban tudjon futni az oroszlán elől. Ezt látva a társa megszólal:
– Hova erőlködsz? Az oroszlán gyorsabb az embernél, úgysem tudsz elfutni előle.
Mire a válasz:
– Nekem nem is az oroszlánnál kell gyorsabban futnom, hanem a nálad." (Pesti vicc)
- hányan játszák a játékokat (lehet két- vagy többszereplős a játék);
- hány döntési alternatíva van a játékosok előtt (lehet két- vagy többalternatívás játék);
- hányszor játszanak egymással a játékosok (lehet egyszer vagy többször játszott, tehát egyszeri vagy ismételt a játék);
- azonosan értékelik-e a játékosok a játékot vagy sem (lehet szimmetrikus vagy aszimmetrikus a játék);
- a preferenciarendezések szigorú rendezésen alapulnak-e vagy sem, vagyis megengedhető-e az, hogy két döntési alternatívát azonosnak minősítsen egy játékos, esetleg egy alternatívát ne értékeljen (lehet szigorúan rendezett vagy nem szigorúan rendezett a játék);
- ismerik-e egymást a játékosok vagy sem, aminek az ismételt játékok esetében van kiemelt jelentősége (lehet direkt vagy indirekt reciprocitás játék);
- kommunikálhatnak-e a játékosok a döntések meghozatala során és ennek során tehetnek-e egymásnak ígéreteket, elköteleződéseket vagy sem (lehet nem-kooperatív, "ígéretmentes" vagy kooparatív, "ígéretes" a játék [♦] });
- egyszerre döntenek-e a játékosok vagy egymás után, egyik a másik döntésének ismeretében (lehet szinkron, szimultán, statikus vagy aszinkron, szekvenciális, alternáló, dinamikus a játék, de ide tartoznak a méltányosságelméletekhez használt alkujátékok is).
$\mathscr{L}_{IL}$($\mathscr{L}_{BL}, \mathscr{L}_{DL})$
| $\mathscr{L}_{BL}$ | preferencialogika |
| $\mathscr{L}_{DL}$ | deontikus logika |
Magjátékok
A társadalmi kapcsolatok játékelméleti modellezését úgy építhetjük fel, hogy kiindulunk a lehető legegyszerűbb, legkisebb méretű társadalom modelljéből, majd lépésenként egyre több kezdeti feltételt "elengedünk", hogy a társadalom egyre összetettebb, egyre bonyolultabb modelljéhez juthassunk. Ebben az építkezésben a preferenciamátrix van a központban. Kiindulásként rögzítjük, hogy egyszerre érvényesül a kétszereplős, kétalternatívás, egyszeri, szimmetrikus, szigorúan rendezett, szinkron, nem kooperatív játékok feltételegyüttese. Ezeket a játékokat korábban magjátékoknak neveztem el [syiDi] és – ahol lehetett – alapos leírást is adtam rájuk (sok példával), ezért itt csak a legfontosabb vonásait mutatom be a játékoknak.| magjátékok | ||||||||||||||
| aszimmetrikus játékok | szimmetrikus | |||||||||||||
| többalternatívás játékok | kétalternatívás | |||||||||||||
| többszereplős játékok | kétszereplős | |||||||||||||
| nem szigorúan rendezett játékok | szigorúan rendezett | |||||||||||||
| aszinkron játékok | szinkron | |||||||||||||
| ismételt játékok | egyszeri | |||||||||||||
| direkt reciprocitás játékok | ismerős játékosok | |||||||||||||
| indirekt reciprocitás játékok | ismeretlen játékosok | |||||||||||||
| kooperatív (ígéret) játékok | nem kooperatív (ígéretmentes) | |||||||||||||
|
$\rightarrowtail$ |
|
$\rightarrowtail$ |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
$\rightarrowtail$ |
| $\rightarrowtail$ |  | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| magának ad | másiknak ad | |||||||||||||
| C | 1 | 2 | ||||||||||||
| D | 2 | 0 | ||||||||||||
| tanul | nem tanul | |||||||||||||
| átmegy a vizsgán | 2 | 3 | ||||||||||||
| megbukik a vizsgán | 0 | 1 | ||||||||||||
Fogolydilemma játék
| 3,3 | 1,4 | |||||||||||||
| 4,1 | 2,2 | |||||||||||||
| \ | ||||||||||||||
| a játék száma | ||||||||||||||
| Rapoport-Guyer: | 12 | |||||||||||||
| Brams: | 32 | |||||||||||||
| Robinson-Goforth: | 111 | |||||||||||||
Mártírjáték
| 3,3 | 4,1 | |||||||||||||
| 1,4 | 2,2 | |||||||||||||
| \ | ||||||||||||||
| a játék száma | ||||||||||||||
| Rapoport-Guyer: | 9 | |||||||||||||
| Brams: | 9 | |||||||||||||
| Robinson-Goforth: | 166 | |||||||||||||
Gyáva nyúl játék
| 3,3 | 2,3 | |||||||||||||
| 4,2 | 1,1 | |||||||||||||
| \ | ||||||||||||||
| a játék száma | ||||||||||||||
| Rapoport-Guyer: | 66 | |||||||||||||
| Brams: | 57 | |||||||||||||
| Robinson-Goforth: | 122 | |||||||||||||
Önkéntes játék
| 3,3 | 4,2 | |||||||||||||
| 2,4 | 1,1 | |||||||||||||
| \ | ||||||||||||||
| a játék száma | ||||||||||||||
| Rapoport-Guyer: | 7 | |||||||||||||
| Brams: | 7 | |||||||||||||
| Robinson-Goforth: | 155 | |||||||||||||
Vezérjáték
| 2,2 | 3,4 | |||||||||||||
| 4,3 | 1,1 | |||||||||||||
| \ | ||||||||||||||
| a játék száma | ||||||||||||||
| Rapoport-Guyer: | 68 | |||||||||||||
| Brams: | 54 | |||||||||||||
| Robinson-Goforth: | 133 | |||||||||||||
Hősjáték
| 2,2 | 4,3 | |||||||||||||
| 3,4 | 1,1 | |||||||||||||
| \ | ||||||||||||||
| a játék száma | ||||||||||||||
| Rapoport-Guyer: | 69 | |||||||||||||
| Brams: | 55 | |||||||||||||
| Robinson-Goforth: | 144 | |||||||||||||
Szarvasvadászat játék
| 4,4 | 1,3 | |||||||||||||
| 3,1 | 2,2 | |||||||||||||
| \ | ||||||||||||||
| a játék száma | ||||||||||||||
| Rapoport-Guyer: | 61 | |||||||||||||
| Brams: | - | |||||||||||||
| Robinson-Goforth: | 322 | |||||||||||||
Háztulajdonos játék
| 4,4 | 3,1 | |||||||||||||
| 1,3 | 2,2 | |||||||||||||
| \ | ||||||||||||||
| a játék száma | ||||||||||||||
| Rapoport-Guyer: | 5 | |||||||||||||
| Brams: | - | |||||||||||||
| Robinson-Goforth: | 355 | |||||||||||||
Koordinációs játék: ügyfél
| 4,4 | 1,2 | |||||||||||||
| 2,1 | 3,3 | |||||||||||||
| \ | ||||||||||||||
| a játék száma | ||||||||||||||
| Rapoport-Guyer: | 63 | |||||||||||||
| Brams: | - | |||||||||||||
| Robinson-Goforth: | 333 | |||||||||||||
Koordinációs játék: balszélső
| 4,4 | 2,1 | |||||||||||||
| 1,2 | 3,3 | |||||||||||||
| \ | ||||||||||||||
| a játék száma | ||||||||||||||
| Rapoport-Guyer: | 60 | |||||||||||||
| Brams: | - | |||||||||||||
| Robinson-Goforth: | 344 | |||||||||||||
Harmóniajáték: csónakos
| 4,4 | 2,3 | |||||||||||||
| 3,2 | 1,1 | |||||||||||||
| \ | ||||||||||||||
| a játék száma | ||||||||||||||
| Rapoport-Guyer: | 6 | |||||||||||||
| Brams: | - | |||||||||||||
| Robinson-Goforth: | 311 | |||||||||||||
Harmóniajáték: pacifista
| 4,4 | 3,2 | |||||||||||||
| 2,3 | 1,1 | |||||||||||||
| \ | ||||||||||||||
| a játék száma | ||||||||||||||
| Rapoport-Guyer: | ||||||||||||||
| Brams: | ||||||||||||||
| Robinson-Goforth: | 366 | |||||||||||||
A magjátékok áttekintése
A tizenkét magjáték között érdekes összefüggések vannak, amelyek még inkább észrevehetőek, ha valamilyen összesítő ábrában mutatjuk meg őket. Tanulságos áttekinteni egyszerre is az egyes játékoknál egyenként bemutatott vizuális reprezentációkat.
Az "útjelzős" ábrán jól látszik, hogy háromféle mintázat van, a z-, az n- és az x-betűs. A függőleges tengelyen van négy játék, melyek középpontjában a fogolydilemma (potyautas) és a harmónia (csónakos) játék van (mellettük ott vannak még a tengelyen a komplementer párjaik). A fogolydilemmaból (és komplementer társából, a mártírjátékból) kaphatjuk meg a gyáva nyúl és a szarvasvadászat játékokat (illetve ezek komplementereit), majd még egy "lépés téve" jobbra , illetve balra eljuthatunk a kétféle nemek harca, illetve kétféle koordinációs játékhoz. A játékok topológiai sajátosságait mutató kis ábrákat egy közös térben feltüntetve és ezáltal az összes magjátékot egyszerre nézve még jobban szembeötlővé válik az a tény, hogy a fogolydilemma (potyautas) játék adja, ígéri a legkisebb nyereményt a játékosok számára. Még a szarvasvadászat játékban fordulhat elő az, hogy a szuboptimális egyensúlyi pontot (2,2) választják a résztvevők, egyébként minden más esetben csak magasabb nyereményekkel lehet a játékokból kijönni. Ha a legfontosabb adatokat mind egy helyen tüntetjük fel, akkor adódik egy harmadik lehetőség is a játékok egyidejű ábrázolására. Valahogy így.
Az ábra elkészítéséhez segítségül hívtam azt a vizuális technikát, amelyet már évezredek óta használ az emberiség személyiségtípusok megjelenítésére. A zodiákus tizenkét állatövi jegyét, tizenkét személyiségtípusát sokszor jelenítik meg kördiagram segítségével. Ezt a megoldást vettem át én is a tizenkét magjáték ábrázolására. Természetesen egy percig sem állítom, hogy bármilyen tartalmi kapcsolat lenne a kétfajta reprezentáció között, kizárólag a vizuális megjelenítés áttekinthetőséget és megérthetőséget könnyítő szerepe miatt veszem igénybe ezt a technikát. Az összes fontos vizuális információt, a játékok preferenciamátrixait és neveit, valamint a Robinson-Gofort könyvben használt azonosítószámokat feltüntettem az ábrában. A magjátékok bemutatása után úgy léphetünk tovább a társadalmi cselekvések játékelméleti modellezésében, hogy egymás után "elengedünk" egyet-egyet a kezdetben megfogalmazott feltételeink közül. Ezáltal a társadalmi kapcsolatok egyre összetettebb modelljéhez jutunk. A modell fokozatos kiterjesztését az alábbi lépésekben fogom elvégezni. Először megmaradok annál a feltételnél, hogy a játékosok csak egyszer találkoznak egymással, vagyis egyszeri játékot játszanak. Ezeket nevezem statikus játékoknak. Ezután a játékok logikai rendjében engedem meg a változtatást azzal, hogy figyelembe veszem a büntetés mint cselekvési alternatíva lehetőségét is. A büntetni csak akkor tudunk, ha van egy azt megelőző – büntetendőnek ítélt – cselekvés. Ehhez el kell engedni a szinkronitás feltételét, vagyis aszinkron játékokat kell elemeznünk. Ha így teszünk, még a statikus játékok világán belül maradunk, hiszen lehetnek egyszeri aszinkron játékok (például az alkujátékok). A következő lépésben lehet dinamikát adni a játékoknak, amit az ismételt játékok segítségével tudunk modellezni. A játékok ismétlésére, a dinamikus szemlélet alkalmazására akkor van módunk, ha a modellünkbe beemeljük a társadalmi emlékezet fogalmát. A játékok ismétlődésének ugyanis az a feltétele (és persze hozadéka is egyben), hogy a játékosok tudják azt, mi történt velük az előző forduló(k)ban, vagyis ki hogyan cselekedett korábban. Első körben a direkt reciprocitás játékokat tárgyalom, amelyekben a játékosok ismerik egymást. Ezt követi az indirekt reciprocitás játékok elemzése, amikor egyfelől a játékosokról nem kell feltételeznünk, hogy ismernék egymást, másfelől viszont a döntési szabályok alátámasztásához szükség lesz az értékelési rendszerek, reputációképző szabályok modellbe emelésére is. A legvégén pedig röviden kitérek majd arra, hogy a koordinációs problémáknak, a koalíciós helyzeteknek milyen különös vonásaik vannak.
A játékok statikus kiterjesztése
A magjátékok tárgyalása utáni modellbővítést a statikus játékokon belül maradva végzem el. Sorban bemutatom, hogy milyen módokon lehet leírni, jellemezni az aszimmetrikus, a többalternatívás, a többszereplős, végül a nem szigorúan rendezett játékokat.Aszimmetrikus játékok
Az aszimmetrikus játékoknak aszimmetrikus preferenciamátrixuk van, minden másban megegyeznek a szimmetrikus játékokkal. A kétszemélyes, kétalternatívás játékok közül csak 12 szimmetrikus, az összes többi aszimmetrikus. Korábban már elmondtam, de nem baj ha itt megismétlem, hogy hosszú időn keresztül széles körben elfogadott volt Rapoport és Guyver nézete, amely szerint 66 aszimmetrikus alapjátékot különíthetünk el egymástól. Ez a szám úgy jött ki, hogy Rapoporték ekvivalensnek minősítették azokat a játékokat, amelyek a két játékos felől nézve ugyanúgy "néznek ki". Ha arra gondolunk, hogy mindegy, hol is "áll" a két játékos, a Sor vagy az Oszlop játékos szerepében játszik-e, akkor ez az ekvivalenciatételezés elfogadható. Ha azonban Egoról és Alterről beszélünk, vagyis elkülönítjük egymástól azt a két szerepet, amelyek közül az egyiket (Egot) kitüntetett helyzetbe tesszük, hiszen mindig az ő cselekvését, döntéseit akarjuk megérteni az adott játék értelmezésekor, akkor már igenis "láthatunk" különbséget két olyan játék között, amelyek közül az egyikben Ego a Sor, a másikban Ego az Oszlop játékos szerepébe kerül. Egonak nem mindegy, hogy az aszimmetrikus helyzet melyik pólusán van. Ezt a szemléletváltást hozta el Robinson és Gofort 2005-ös könyve [Robin] és ezt fogadom el én is. Ebből következően az alapjátékok száma 144, az aszimmetrikus játékoké pedig 132.| magjátékok | ||||||||||||||
| aszimmetrikus játékok | aszimmetrikus | |||||||||||||
| többalternatívás játékok | kétalternatívás | |||||||||||||
| többszereplős játékok | kétszereplős | |||||||||||||
| nem szigorúan rendezett játékok | szigorúan rendezett | |||||||||||||
| aszinkron játékok | szinkron | |||||||||||||
| ismételt játékok | egyszeri | |||||||||||||
| direkt reciprocitás játékok | ismerős játékosok | |||||||||||||
| indirekt reciprocitás játékok | ismeretlen játékosok | |||||||||||||
| kooperatív (ígéret) játékok | nem kooperatív (ígéretmentes) | |||||||||||||
Többalternatívás játékok
A kétalternatívás játékok abban az értelemben nagyon egyszerű társadalomképet feltételeznek, hogy ebben a világban csak "igen-nem" döntések hozhatnak a játékosok. Sok esetben elég ez a megoldás. De természetesen nem kevésszer kerülhetünk olyan helyzetbe, amelyekben a döntéseink nem ilyen egyszerű szerkezetűek, amikor több alternatíva közül kell választanunk. Gondoljunk csak a kő-papír-olló néven ismert, egyébként nagyon egyszerű játékra, amelyben három döntési lehetőség közül kell választaniuk a játékosoknak. Az ilyen helyzeteket a többalternatívás játékokkal modellezhetjük.| magjátékok | ||||||||||||||
| aszimmetrikus játékok | szimmetrikus | |||||||||||||
| többalternatívás játékok | többalternatívás | |||||||||||||
| többszereplős játékok | kétszereplős | |||||||||||||
| nem szigorúan rendezett játékok | szigorúan rendezett | |||||||||||||
| aszinkron játékok | szinkron | |||||||||||||
| ismételt játékok | egyszeri | |||||||||||||
| direkt reciprocitás játékok | ismerős játékosok | |||||||||||||
| indirekt reciprocitás játékok | ismeretlen játékosok | |||||||||||||
| kooperatív (ígéret) játékok | nem kooperatív (ígéretmentes) | |||||||||||||
Többszereplős játékok
A többalternatívás játékok modellezése nagyon könyen megoldható a kétalternatívás döntéssorozat technikájának alkalmazásával. Nem ez a helyzet a többszereplős játékok esetében. Sok minden megváltozik ugyanis akkor, amikor a társadalmat már úgy modellezzük, hogy két játékos helyett sok szereplő alkotja azt. Ezt a lépést meg kell tennünk, mert bár sokszor találhatjuk magunkat kétszemélyes játékszituációkban, de még többször kerülünk olyan helyzetekbe, amikor a helyzet minősítő sajátossága az, hogy sokan, nagyon sokan vagyunk benne.| magjátékok | ||||||||||||||
| aszimmetrikus játékok | szimmetrikus | |||||||||||||
| többalternatívás játékok | kétalternatívás | |||||||||||||
| többszereplős játékok | többszereplős | |||||||||||||
| nem szigorúan rendezett játékok | szigorúan rendezett | |||||||||||||
| aszinkron játékok | szinkron | |||||||||||||
| ismételt játékok | egyszeri | |||||||||||||
| direkt reciprocitás játékok | ismerős játékosok | |||||||||||||
| indirekt reciprocitás játékok | ismeretlen játékosok | |||||||||||||
| kooperatív (ígéret) játékok | nem kooperatív (ígéretmentes) | |||||||||||||
Nem szigorúan rendezett játékok
Elméleti szempontból érthetőnek és könnyen elfogadhatónak tűnik az az elvárás, amely szerint feltételezzük, hogy a játékosok egyértelműen sorba tudják rendezni a játék lehetséges kimeneteit, alternatíváit. A preferenciarendezésre vonatkozó szigorú rendezési feltétel azonban a tényleges gyakorlatban sok esetben túlzottan szigorú elvárásnak minősül. Nem tudunk mindig minden alternatívát egyértelműen sorba rendezni. Van, hogy nem tudunk valamely alternatívát megítélni és egyszerűen kihagyunk a rendezésből, de az is előfordul, hogy nem vagyunk képesek dönteni két vagy több alternatíva esetében, és ilyenkor "döntetlenre hozzuk ki" a sorrendet köztük. Az ilyen esetek modellezésére az olyan játékok alkalmasak, amelyekben nem követeljük meg a szigorú rendezés feltételének fennállását.| magjátékok | ||||||||||||||
| aszimmetrikus játékok | szimmetrikus | |||||||||||||
| többalternatívás játékok | kétalternatívás | |||||||||||||
| többszereplős játékok | kétszereplős | |||||||||||||
| nem szigorúan rendezett játékok | nem szigorúan rendezett | |||||||||||||
| aszinkron játékok | szinkron | |||||||||||||
| ismételt játékok | egyszeri | |||||||||||||
| direkt reciprocitás játékok | ismerős játékosok | |||||||||||||
| indirekt reciprocitás játékok | ismeretlen játékosok | |||||||||||||
| kooperatív (ígéret) játékok | nem kooperatív (ígéretmentes) | |||||||||||||
A játékok magasabbrendű kiterjesztése büntetéssel
A játékelmélet első szintjén a játékosok stratégiáit úgy értékeljük, hogy a cselekvések (döntések) tartalmát absztraháljuk, vagyis lecsupaszítjuk a kooperálás-dezertálás dichotómiájára. A kooperálás a jó, a dezertálás a rossz, és az a nagy kérdés, hogy mikor, hogyan, miért lehet elérni, remélni, hogy kooperáljanak a játékosok. Ez a séma persze nem pontos. Hiszen a koordinációs játékoknál láthattuk, hogy a kooperálás vagy dezertálás fogalma már nem használható tartalmas módon. Az összes alapjátékra igaz viszont, hogy ha van valamilyen feloldandó társadalmi dilemma vagy koordinációs probléma, akkor mindig van olyan kimenet, amely jobb, kívánatosabb a többinél, és a kérdés úgy szól, hogy milyen eszközzökkel lehet biztosítani a társadalmilag kívánatosnak tartott kimenetek követését. Az egyik válasz a döntések szankcionálása. Ismételt vagy aszinkron játékok esetében, amikor az egyik játékos ismerheti a másik döntését, szankcionálhatja a már ismert döntést, vagyis saját cselekedetét a másik játékos előző döntéséhez igazíthatja. Mancur Olson vezette be a szelektív ösztönző (selective incentive) fogalmát [olson] de tovább már nem pontosította. A fogalom alapos elemzését Pamela Oliver végezte el [olive] [olive] aki meggyőzően mutatta be azt, hogy milyen helyzetekben lehet hatásosan alkalmazni a pozitív ösztönzőket, azaz a jutalmakat (reward), és mikor a negatív ösztönzőket, azaz a büntetéseket (punishment). Több, más szempont mellett az egyik legfontosabb szempont a kollektív javak előállításához szükséges emberek számosságának kérdése. Amennyiben kevés ember hozzájárulása elegendő lehet (például egy kisvárosi újság finanszírozásához), akkor a pozitív ösztönzés elégségesnek bizonyulhat (kitüntetést adni a kevés támogatónak), de minél nagyobb létszámú hozzájárulóra van szükség, annál inkább csak a negatív ösztönzés lesz működőképes (például a sztrájktörés megakadályozására). Bár a hétköznapi szóhasználatban ritkán fordul elő, de legalábbis idegenül hangzik a negatív ösztönzés terminusa, de ugyanúgy szokatlannak lehet tartani a pozitív szankció kifejezését is, pedig a szankcióra is ráhúzhatjuk a pozitív vagy negatív minősítéseket, hogy azokkal a jutalmazás vagy büntetés jelenségét jelezzük. A továbbiakban én a pozitív és negatív ösztönzés, illetve szankció, valamint a jutalom és büntetés terminusait egymással felcserélhető módon fogom használni. Azt is jeleznem kell azonban, hogy a későbbiekben gyakorlatilag csak a büntetés jelenségét fogom figyelembe venni a modellek felépítése során, és a jutalmazás intézményét hanyagolni fogom. Az ösztönzés, szankcionálás fogalmát, különösen annak negatív változatát, azaz a büntetést el kell tudnunk választani a "puszta" károkozás, "sima" agresszió jelenségétől. Ezt akkor tudjuk megtenni, ha felismerjük azt, hogy a büntetés (és jutalmazás) jelenségében van egy logikai értelemben magasabbrendű minőség.Másodrendű játékok – költséges büntetés
A legáltalánosabb szempont szerint a szankcionálásnak két típusa lehetséges, a pozitív, illetve a negatív szankció. A negatív szankció vagyis a büntetés a rossz, nem kívánatos cselekvésre adott negatív tartalmú válasz. A pozitív szankció ennek ellentéte, vagyis a kívánatos cselekvésre adott pozitív tartalmú válasz. Pozitív és negatív válaszokon azt kell itt érteni, hogy a szankcionált fél számára előnyökkel vagy hátrányokkal jár-e az alkalmazott szankció. A szankció alkalmazásának nyilván az lehet a célja, hogy a másik felet valamely cselekvés folytatásra vagy épp az attól való tartózkodásra lehessen bírni. Ha csak ennyiben állna a dolog, akkor egyszerű lenne a helyzet, hiszen a szankcionálás révén remélni lehetne a kívánatos állapotok elérését. Azonban a szankció mindkét fajtája költségekkel jár a szankciót alkalmazó ágens számára, és ez újfajta problémát eredményez a játékelméleti modellezés számára. Azzal ugyanis, hogy figyelembe kell venni a szankciónak, büntetésnek a költségeit, fel kell tenni a kérdést, hogy kik lesznek azok, akik magukra vállalják ezeket a szankcionálási költségeket, amelyeknek a közösség számára lehetnek ugyan előnyei, de a szankció költségeit viselő egyén számára biztosan olyan egyedi terheket jelentenek, amiért közvetlen hasznot nem remélhetnek. Ez a probléma vezette el a kutatókat, hogy megalkossák a másodrendű fogolydilemma játék fogalmát, amelyben az elsőrendű fogolydilemmát a szankcionálással feloldani próbáló másodrendű szankcionálási játékban ugyanolyan – immár másodrendű – dezetálási hajlammal szembesülhetünk, mint ami a "hagyományos", elsőrendű fogolydilemmát jellemzi [olive] [Panch] Ki fogja a költséges büntetést elvégezni a köz érdekében – ez a másodrendű fogolydilemma fő kérdése. Azért kell itt másodrendű fogalomról beszélnünk, mert a büntetésről csak úgy van értelme beszélni, ha azt egy előző, a büntetni kívánt cselekvésre vonatkoztatjuk. A büntetés leírásakor mindig meg kell tudnunk adni, hogy milyen korábbi cselekvést szankcionál, ami azt jelenti, hogy egy cselekvést (a büntetést) úgy tudunk leírni, hogy a paraméterei közt megadunk egy másik (a büntetendő) cselekvést, vagyis másodrendű fogalmat képzünk. Az általános kép felfestése után érdemes picit a részletekben is elmerülni, és megvizsgálni azt, hogy milyen módon próbálják meg tipizálni a büntetések világát a szakirodalomban. Arra fókuszálva, hogy a büntetendő cselekvés valakinek valamilyen sérelmet okozhatott, jellemezhetjük aszerint a büntetéseket, hogy ki hajtja végre a büntetést. Amennyiben a sértett, akkor sértetti büntetésről (second-party punishment – 2PP) beszélhetünk, ha viszont egy harmadik személy, aki nem volt közvetlenül érintett az eseményben, akkor kívülálló büntetésről (third-party punishment) lehet szó [Ernst] Az, hogy milyen motívumok miatt büntetnek (altruista, agresszív stb.), itt másodlagos kérdés. Meg lehet különböztetni egymástól a csoporton belüli (within-group) és a csoporton kívüli, csoportok közötti (inter-group) büntetést. Az evolucionalista magyarázat szerint a csoportok közti versengésben alakulhat ki és szilárdulhat meg a kooperáció (altruizmus) jelensége (☜) Egyes kutatók szerint a csoportok közti versengésben, konfliktusokban gyakran megjelenhet a parokiális altruizmus (parochial altruism) jelensége, ami azt jelenti, hogy valamilyen szempont szerint összetartozó csoport tagjai erősebben védelmezik magukat a kívülről érkező, nem kívánatos, ártó, büntetendő cselekvésekkel szemben a büntetés eszközével [Helen] A büntetés motivációjára vonatkozóan versengő elméletek léteznek. N.J. Raihani és K. McAuliffe kísérleteik alapján azt állítják [N.J.R] hogy a csalás megbüntetésének szándékát nem pusztán a csalás ténye váltja ki, így nem annak viszonzásáról, tehát nem negatív reciprocitásról van szó, hanem az ítélkezők a csalás megtörténte után azt is figyelembe veszik, sőt, elsősorban azt veszik figyelembe, hogy miként változott saját kifizetésük a csalóéhoz képest a csalás után (és következtében), és csak akkor büntetnek, ha az így észlelt egyenlőtlenséget nem tartják elfogadhatónak. Ernst Fehr, Urs Fischbacher és Simon Gächter megkülönbözeti a stratégiai és a nem stratégiai büntetéseket egymástól [Ernst] A stratégiai büntetés motivációját nem érzelmi tényezők adják, hanem inkább az a racionális megfontolás, hogy a büntetés által növelni lehet a saját haszon nagyságát a többi játékos nyereségének rovására. Fehrék megkérdőjelezik e büntetési forma széleskörű elterjedtségét. Ezzel szemben a nem-stratégiai büntetés motivációs hátterét a társadalmi normák be nem tartása miatt keletkező érzelmek biztosítják. Ilyen esetekben a büntetés célja a megsértett társadalmi normák betarttatása, az elvárt viselkedés kikényszerítése. Más szerzők szerint előfordulhatnak olyan esetek, amikor a büntetés motivációjaként rosszindulatot, agressziót (spite) vagy az irigységet (envy) lehet kimutatni. Gyakran olyan játékosok, kísérleti alanyok büntetnek így, akik a partnerüket túl "veszélyes" vetélytársuknak tekintik, akik hozzájuk képest sikeresebbek, és fenyegetik az érdekeiket [FalkA] [FehrE] Egy másik fejezetben bemutatom a méltányosságelméletekhez kapcsolható kísérleti játékokat (☜) amelyek nagy részében megtalálhatjuk (sőt mérni lehet) a büntetés jelenségét, és ott bizony az egyik lehetséges magyarázat a – valamilyen értelemben vett – destruktív magatartás (☜) Ilyen esetekben könnyen előfurdulhat az, hogy valaki maga számára kis veszteséggel másoknak nagyon nagy károkat képes okozni [FalkA] ugyanakkor ezen kísérletek másik nagy tanulsága az, hogy sok esetben igen nagy személyes veszteséget is hajlandóak az emberek magukra vállalni csak azért, hogy büntethessék partnerük méltánytalannak érzett cselekedeteit.Szankcióparadoxon
A büntetés funkcióját azzal magyarázhatjuk, hogy a kívánatos cselekvési mintákat azáltal (is) reméljük általánossá tenni és fenntartani a társadalomban, hogy büntetjük a nem kívánatos cselekvési formákat, amihez persze szükséges, hogy legyenek, akik magukra vállalják a dezertálók büntetését (annak költségeit). Ezen a ponton azonban egy furcsa paradoxonnal kell szembenéznünk. Ha ugyanis: (i) a büntetés "célja" általában a dezertáló, a nem-segítőkész magatartás szankcionálása, viszont (ii) a büntetés maga mindig valamilyen nem kívánt jelenség kiváltását, a segítésnyújtás megtagadását vagy testi, lelki erőszak alkalmazását jelenti, vagyis (iii) a büntetés tartalmát önmagában megítélve rossznak, dezertálásnak kell minősítenünk, akkor konstatálhatjuk, hogy e három tétel között ellentmondás feszül. Ezt többféleképpen lehet értékelni. Ha mindenekfölött álló értéknek tartjuk a segítést, a kooperálást, akkor nem szabad büntetni senkit, mert az nem kooperatív hozzáállás. Ezzel az elvvel azt lehet szembeállítani, hogy ha nem büntetünk, akkor ezzel "jóváhagyjuk" mások dezertálását, helytelen magatartását, ami a kooperáció fenntartása, a közösség egésze szempontjából nem előnyös. Ha erre az érvre hivatkozva mégiscsak büntetünk, akkor árnyalni kell a büntetést végrehajtó személy megítélését, hiszen ebből a szempontból mondhatjuk, hogy a büntető a közösség érdekét követve büntet. Ha így tesz valaki, akkor a büntetés "jogos, igazolt", amit szembe lehet állítani azzal a helyzettel, amikor valaki "jogtalan, igazolatlan" módon büntet. Ez pedig megkívánja, hogy beemeljük a modellünkbe a diszkrimináció jelenségét (és fogalmát), hiszen különböző irányban, különböző megítélésű szereplőkkel szemben másként kell alkalmazni a büntetés eszközét. [♦] Ez a paradox jelleg a büntetés másodrendű voltából fakad. Szemléletessé tehetjük ezt egy táblázat segítségével, ha abban feltüntetjük, hogy a cselekvések kétféle rendjében, kétféle szintjén milyen döntések elé kerülhetnek a cselekvők, és milyen cselekvési lehetőségeket lehet elkülöníteni egymástól.| másodrendben kooperál, büntet | másodrendben dezertál, nem büntet | |||||||||||||
| első rendben kooperál | kooperál és büntet | kooperál, de nem büntet | ||||||||||||
| első rendben dezertál | nem kooperál, de büntet | nem kooperál és nem is büntet | ||||||||||||
| másodrendben kooperál | másodrendben dezertál | |||||||||||||
| (büntet = nem segít) | (nem büntet = segít) | |||||||||||||
| első rendben kooperál (segít) | elsőrendben segít, másodrendben nem segít | elsőrendben segít, másodrendben segít | ||||||||||||
| első rendben dezertál (nem segít = büntetés | elsőrendben nem segít, másodrendben nem segít | elsőrendben nem segít, másodrendben segít | ||||||||||||
Aszinkron játékok
A magjátékok kevésbé reflektált, kevesebbet elemzett feltétele a játékok szinkronitásának elvárása. Pedig vannak olyan esetek, amelyekben nem tartható fent ez a feltétel. A szimultán játszott, szinkron jellegű játékokkal szembe állíthatóak azok a helyzetek, amelyekben az aszinkron (szekvenciális, alternáló) döntéshozatal a jellemző. Ekkor a játékosok nem egyszerre, szimultán módon hoznak döntést, hanem egymás után, így a másik döntésének ismeretében választanak az alternatíváik közül.| magjátékok | ||||||||||||||
| aszimmetrikus játékok | szimmetrikus | |||||||||||||
| többalternatívás játékok | kétalternatívás | |||||||||||||
| többszereplős játékok | kétszereplős | |||||||||||||
| nem szigorúan rendezett játékok | szigorúan rendezett | |||||||||||||
| aszinkron játékok | aszinkron | |||||||||||||
| ismételt játékok | ismételt | |||||||||||||
| direkt reciprocitás játékok | ismerős játékosok | |||||||||||||
| indirekt reciprocitás játékok | ismeretlen játékosok | |||||||||||||
| kooperatív (ígéret) játékok | nem kooperatív (ígéretmentes) | |||||||||||||
Alkujátékok
Az aszinkronitást nem csak az ismételt játékok esetén lehet feltételeznünk. A kísérleti közgazdaságtan, viselkedés-gazdaságtan vizsgál olyan helyzeteket is, amelyek csak egyszer játszott játékoknak felelnek meg, ám a játékosok nem egyszerre, hanem egymás után döntenek, így a későbbi döntéshozók már ismerik a partnereik választásait. Ezeket is aszinkron helyzeteknek minősíthetjük. Az ilyen játékokat a kísérleti közgazdaságtan régóta és elég nagy intenzitással vizsgálja, igaz, nem elősorban a helyzetek aszinkronitása miatt, hanem inkább azért, mert ezekben a játékokban jól lehet vizsgálni a kísérleti alanyok beállítódásait, értékelköteleződéseit, normatív struktúráit. Ezért tárgyalhatnám máshol is ezeket a játékokat, [♦] (☜) de mivel vannak érvek amellett, hogy itt szerepeljenek, ezért itt mutatom be őket. Problémásnak érzem a játékok általános megnevezését is. A szakirodalomban gyakran alkujátékoknak (bargaining games-nek) nevezik az ilyen játékokat, ami több szempontból is vállalható, megmagyarázható, de az alkuelmélet kifejezéssel párba állítva már kicsit félrevezetőnek, könnyen félreérthetőnek tartom az alkujátékok terminusát. Az 'alku' fogalmának kétszeres használatával "sugallt" szemantikai közelség itt félrevezető, mert amíg az alkuelmélettel egy folyamatot, egy procedurát írunk le, addig az alkujátékok az egyének beállítódásainak egyszeri kinyilvánításait "mérik". Mivel azonban az alkufolyamat mélyén is ott lapulnak az alkudozó egyének beállítódásai, értékelkötelződései, ezért – fenntartásokkal ugyan, de – elfogadhatónak tartom az alkujátékok megnevezés használatát. Az is amellett szól, hogy az alkujátékokat ebben a fejezetben tárgyaljam, hogy ezek aszinkron játékok. A játékosok itt egyszemélyes játékokat játszanak szekvenciális módon." … az ultimátum (alku) játékokban a stratégiai interakció pusztán a jövőbeni döntések előrejelzésében testesül meg. Itt nincs az egyidejű lépések és végtelen játéksorozat tényéből fakadó kölcsönös függősség (interdependencia)." [Werne]
Ezekben a játékokban a méltányosság (fairness, equity) jelenlétét, mértékét, százalékokban is kifejezhető erősségét keresik. Azt vizsgálják, hogy milyen mértékű a másik személy iránti reciprok beállítódás mértéke, azaz mennyire hajlandó a kísérleti személy kooperálni a másikkal (lemondani saját előnyei egy részéről a másik javára), illetve hajlandó-e büntetni a másikat, ha az nem kooperál, még akkor is, ha a büntetés saját magának költségbe kerül. Mivel a személyiségben rejtőzködő reciprocitási hajlamot vizsgálják, gyakran nevezik erős reciprocitás (strong reciprocity) elméletnek ezt a vizsgálati irányt. Egyszeri és ismételt játékok egyaránt előfordulnak, az a közös bennük, hogy empirikus kísérleteken, vizsgálatokon alapul az egész. Éppen ezért ezek az empirikus vizsgálatok nagyon szépen kiegészítik a formális játékelméleti modellek, gondolatkísérletek eredményeit. Nagyon sok kultúrában, szubkultúrában elvégezték, megismételték már a leghíresebb kísérleteket, és nagyjából hasonló eredményeket kaptak – akárhol is, akármilyen kultúrában is gyűjtötték az adatokat. Természetesen a különböző kultúrákban, szubkultúrákban felvett adatok között volt különbség, ami fontos vizsgáltai kérdéseket vet, vetett fel, de az erős reciprocitás elmélet körébe tartozó kísérletek talán legfontosabb tanulsága az az általánosíthatónak tűnő állítás, miszerint minden kultúra valamilyen mértékben beleteszi, beleneveli a tagjaiba a reciprocitásérzet, a méltányosságérzet valamilyen fokát. Ez a tétel pedig megintcsak azt a közgazdaságtan világán belül széles körben elterjedt vélekedést kezdi ki, amely szerint az ember – alapértelmezés szerint – önző beállítódással lép másokkal kapcsolatba. A következőkben röviden bemutatom az ultimátumjátékot, a diktátorjátékot, a nyilvános javak játékát és a bizalmi játékot.Ultimátumjáték
Az alkujátékok talán legismertebb és egyben paradigmatikus példája az ultimátumjáték (Ultimatum Game – UG). A játék lényege a következő. [♦] Adott összegből (i) az egyik játékos, az ajánlattevő (Proposer, Allocator) javaslatot tesz a másik játékos, a kedvezményezett (Responder) számára, hogy milyen arányban osztaná fel kettejük között a pénzt (i-c, illetve c). A második lépésben a másik játékos csak annyit tehet, hogy az ajánlatot elfogadja vagy visszautasítja. Amennyiben elfogadja, akkor mindketten megkapják az ajálattevő által javasolt összeget, visszautasítás esetén egyikük sem kap semmit.
A játék azért keltett (és kelt a mai napig) meglepetést sokakban, mert tisztán önérdekkövető játékosokat feltételezve már a legkisebb ajánlatot is el kellene fogadniuk a kezdeményezetteknek, ám a kísérletek tanulságai szerint ennél jóval magasabb ajánlatot fogadnak csak el átlagosan a játékosok. Az előzetes "elméleti" megfontolások alapján ugyanis azt lehet feltételezni, hogy a racionális (és önző) beállítódású kedvezményezettek úgy gondolkozhatnak, hogy a legkisebb egységnyi ajánlat is több, mint a semmi (amit a visszautasítás esetén kapnának), ezért érdemes elfogadni bármilyen ajánlatot, ami a nullánál több. Ezt tudva az ajánlattevők is gondolkozhatnak hasonlóképpen és nyugodtan adhatják a legkisebb ajánlatot. A kísérletek azonban egészen más eredményeket hoztak, hoznak. Az eddigi felmérésekben (kultúráktól függően) 20-50 százalék között mozgott mindenhol az átlagos ajánlattétel nagysága.
A kísérletek tanulsága szerint ezeket a helyzeteket nem lehet leírni a racionális és önző ember hipotézisére támaszkodva. Valami más magyaráző tényezőt kellett tehát találni. Ezen a ponton lehetett felvenni az ember, a társadalom modelljébe a méltányosságérzet fogalmát. Az emberben levő méltányosságérzettel tudjuk csak megmagyarázni az a büntetési szándékot, ami a visszautasítások tényében érhető tetten. A kedvezményezettek ugyanis saját anyagi érdekeikkel szemben vállalják a visszautasítást, ami így büntetésként fogható fel, hiszen így az ajánlattevő sem kap semmit a méltánytalan ajánlata miatt. A kedvezményezettben létezik valamiféle méltányosságérzet, ami meghatároz egy elfogadható ajánlati százalékot, és ha a konkrét ajánlat ennél az összegnél kisebb, akkor a kedvezményezett ezt a partner önzésének tudja be, és a méltánytalan ajánlatot visszautasítással bünteti. Az ajánlattevők pedig ezt a helyzetet racionálisan mérlegelve részben a büntetéstől (és ezáltal a teljes veszteségtől) való félelmükben, részben a bennük is létező méltányosságérzettől vezéreltetve elmozdulnak a fele-fele (fifty-fifty) elv irányába.
Diktátorjáték
A diktátorjáték (Dictator Game – DG) neve nagyon félrevezető, mert a játéknak nincs semmi köze a diktátorsághoz, a diktátori szerephez. Nyilván csak azt akarták kifejezni ezzel a névvel, hogy ebben a játékban egyszemélyi döntésről van szó, a másiknak nincs beleszólási lehetősége a döntésbe. A diktátorjáték hasonlít az ultimátumjátékhoz.
A különbség csak annyi közöttük, hogy a kedvezményezettnek nincs mérlegelési joga a második lépésben. Pontosabban nincs második lépés, vagyis az ajánlattevő ajánlata a játék végeredménye, a javak végleges megosztása is egyben. A kedvezményezetnek semmilyen formában nincs módja befolyásolni a végeredményt. Mivel ezt tudja az ajánlattevő is, ezért arra lehetne számítani az ilyen kísérletek előtt, hogy itt már igenis érvényesülhet az önző racionális ember hipotézise, és az ajánlattevők a minimális ajánlat környékén teszik majd meg ajánlataikat.
Az eredmények azonban mégsem ezt mutatják. Bár már kisebb mértékben, mint az ultimátumjátékban, de még mindig elég magas arányban ajánlanak fel összeget a kedvezményezett számára. Még akkor is (vagy inkább: annak ellenére is) így van ez, hogy ezekben a helyzetekben már azt sem lehet feltételezni, hogy a "büntetéstől" való félelem miatt lennének nagylelkűek az ajánlattevők. Ezek a kísérletek egyértelműen az ajánlattevő altruista beállítódását mérik (és mutatják egyben).
Nyilvános javak játék
A nyilvános javak játék (Public Goods Game – PGG) felfogható az előzőek sokszereplős kiterjesztéseként is (nevezik Simultaneous-Decision Prisoners' Dilemma játéknak is).
Van x (az egyszerűség és összehasonlíthatóság kedvéért legyen megint csak 2) játékos (Ego és Alter), mindegyiknek van valamennyi pénze (i), és mindenki beadhat a közösbe valamennyi pénzt (legyen ez c és d). Az egyéni döntések után a közös kasszába tett teljes összeget megtöbbszörözik (m), és a közös javakból egyenlő arányban visszakapják a játékosok a saját részüket. A kísérleti eredmények szerint kezdetben nagy az altruista hajlam a játékosokban, de idővel (vagyis a játékok számának növekedésével párhuzamosan) ez a kooperatív hajlandóság csökken. A kezdetben mért 40-50%-os felajánlások leesnek nulla közeli értékekre. Az is kiderült azonban ezekből a felmérésekből, hogy ha bevezetik a büntetés lehetőségét (amikor a játékosok saját pénzükből büntethetik a potyautasokat vagyis azokat a társaikat, akik keveset ajánlottak fel a közösbe, akkor a csoport egészén belül jelentősen megugrik a kooperálási hajlandóság. Erre a játékra is igaz, hogy a világ minden pontján, sokféle kultúrán belül elvégezték a kísérleteket, és mindenhol nagyjából hasonló eredményeket kaptak. Ez a játék sokban hasonlít a fogolydillema játékosztályba tartozó 100 dolláros játékhoz (bár nem azonos vele), amelynek a döntési folyamatábrája a következő.
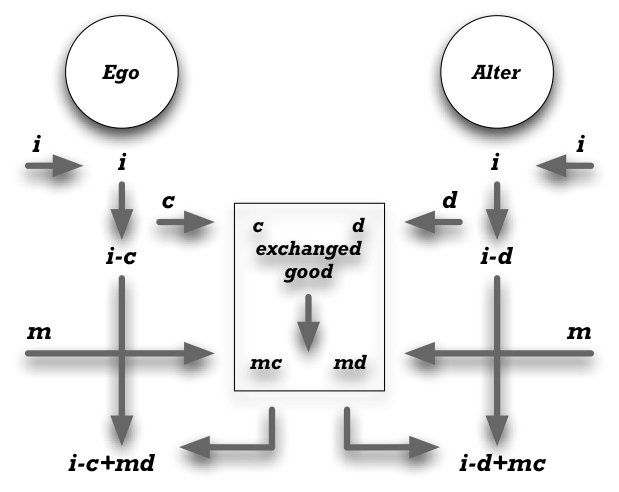
Bizalomjáték
A bizalomjáték (Trust Game – TG, Investment Game – IG) név alatt más játékot értenek az alkujátékok, az erős reciprocitás elméletében, mint a kétszemélyes magjátékok körében, ahol az egyik magjátékot is ezzel a névvel illetik.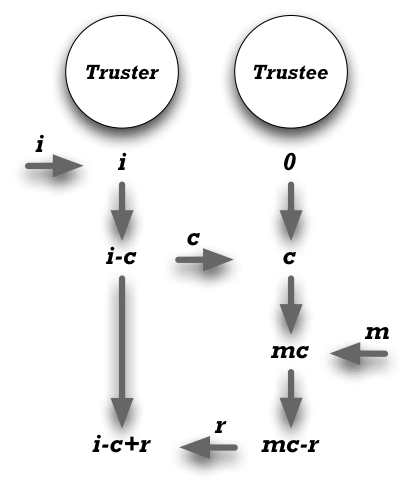
Ebben a játékban is két játékos tesz ajánlatokat egymásnak. Az ajánlattevő lépése előtt a kedvezményezett (Truster) kap egy összeget (i), amiből lehetősége van egy részösszeget (c) "visszaajánlani" a partnerének (Trustee). Ezt az előajánlott összeget megtöbbszörözik (m), és a megnövelt összegű pénzt az ajánlattevőnek meg kell osztani kettejük között, amiből a kedvezményezett visszakap valamit (r).
A játék konstrukciója olyan, hogy leginkább a viszonzási hajlandóságot, a negatív reciprocitást lehet mérni benne, hiszen az ajánlattevő (akinek a viselkedését vizsgálják) az őt ért impulzus (az előzetes ajánlat) hatására dönt (legalább részben). Ebben a kísérleti játékban is az előző játékokhoz hasonlóakat tapasztaltak, vagyis a mérési eredmények szerint az ajánlattevő személyekben – kisebb, nagyobb mértékben – jelen van az altruizmus.
A bevezetőben jeleztem, hogy magam is vitatható döntésnek tartom, hogy a méltányosságelméleteket az aszimmetrikus játékok fogalma alá sorolom. Vitathatóságánál tán csak a szokatlansága nagyobb e döntésnek. Nem lehet vita azonban azzal az elkülönítéssel (és besorolással), amivel a az eddig tárgyalt egyszer játszott, tehát statikus játékokat és a most tárgyalandó ismételt, tehát dinamikus játékokat elválasztjuk egymástól.
A játékok dinamikus kiterjesztése emlékezettel
Ha elengedjük az egyszer játszott játékok feltételét, akkor ismételt játékokhoz jutunk. Ekkor ugyanazt a játékot többször lejátszák egymással a játékosok, vagyis játék helyett játéksorozatot kell vizsgálni. Az egyes játékokat fordulóknak is nevezhetjük, és szükségünk lesz a stratégia fogalmának átértelmezésére is.| magjátékok | ||||||||||||||
| aszimmetrikus játékok | szimmetrikus | |||||||||||||
| többalternatívás játékok | kétalternatívás | |||||||||||||
| többszereplős játékok | kétszereplős | |||||||||||||
| nem szigorúan rendezett játékok | szigorúan rendezett | |||||||||||||
| aszinkron játékok | szinkron | |||||||||||||
| ismételt játékok | ismételt | |||||||||||||
| direkt reciprocitás játékok | ismerős játékosok | |||||||||||||
| indirekt reciprocitás játékok | ismeretlen játékosok | |||||||||||||
| kooperatív (ígéret) játékok | nem kooperatív (ígéretmentes) | |||||||||||||
$\concept{G}\equiv \concept{G}(x,t_i) \equiv \concept{GOOD}(x,t_i)\defi \concept{VALUE}(x,t_i)=Good$
jó (hun) – good (eng)
$\concept{B}\equiv\concept{B}(x,t_i)\equiv \concept{BAD}(x,t_i) \defi \concept{VALUE}(x,t_i)=Bad$
rossz (hun) – bad (eng)
$\concept{B}(x,t_i) \leftrightarrow \neg \concept{G}(x,t_i)$
jó és rossz dichotómiája (hun) – dichotomy of good and bad (eng)
$\concept{DO}(agent,a,t_i)\to (\concept{G}(a,t_i) \leftrightarrow \neg \concept{B}(a,t_i))$
jó és rosz cselekvés dichotómiája (hun) – dichotomy of good and bad action (eng)
$\concept{C}\equiv\concept{C}(agent,t_i)\equiv\concept{COOPERATION}(agent,t_i) \defi \concept{DO}(agent,a,t_i) \land \concept{VALUE}(a,t_i)=Good$
kooperáció (hun) – cooperation (eng)
$\concept{D}\equiv\concept{D}(agent,t_i)\equiv\concept{DEFECTION}(agent,t_i) \defi \concept{DO}(agent,a,t_i) \land \concept{VALUE}(a,t_i)=Bad$
dezertálás (hun) – versengés (hun) – defection (eng)
$\concept{D}(agent,t_i) \leftrightarrow \neg \concept{C}(agent,t_i)$
kooperáció és dezertálás dichotómiája (hun) – dichotomy of cooperation and defection (eng)
Az ismételt játék n lépésig (fordulóig) tart, és a stratégiát leíró szabálynak meg kell adnia minden i. lépésre (vagy másként: mindent $t_i$ időpontra), hogy Ego mit lép. A feltételes cselekvési stratégiák olyan formulákkal írhatók le, amelyekbe valamelyik ágens korábbi cselekvése is be van ágyazva paraméterként, míg a stratégia szabály jellegét a deontikus operátor ($\rel{O}$) fogja jelezni.Reciprocitás
A feltételes stratégia (cselekvési szabály) összekapcsol két döntést, a jelen aktuális döntését a múlt vagy a jövő döntésével (esetleg döntéseivel). A feltételes stratégia így egymásra "feleselő", egymásra hivatkozó döntéseket, cselekvéseket köt össze, és ezzel lehetővé teszi azt, hogy modellezni tudjuk a reciprocitás jelenségét. A reciprocitás fogalmát cselekvések időben eltolt viszonzási rendszereként értelmezve a feltételes szabály fogalmával tudjuk megragadni a reciprocitás legfontosabb összetevőjét. A reciprocitás jelenségében ugyanis összekapcsolódik az aktuális – jelenbeni – döntés/cselekvés a múltbeli, illetve a jövőbeni döntésekkel/cselekvésekkel, a jelen, a jövő és a múlt összerendelése adja az időben eltolt viszonzási rendszer lényegét (lásd Gouldner cikkét a reciprocitás értelmezéséről [gould] Fontosnak tartom azonban megjegyezni, hogy egy szempontból nagyon félrevezető itt reciprocitásról beszélni. A reciprocitás fogalmának gouldneri értelmezése ugyanis normatív szinten zajlik (Gouldner összekapcsolódó jogosultságokról és kötelezettségekről beszél), míg a játékelméletnek ezen a szintjén még sehol nincsenek normák. A feltételes szabályokban megtestesülő szankciók, a jutalomként felfogható kooperációk, illetve a büntetésként felfogható dezertálások bár nyilván hasonlítanak a normativitás lényegi mozzanatát alkotó szankcionálási mechanizmushoz, de van egy nagy különbség. A játékelméletben itt még nincs norma, nincs előre rögzített előírás, nincs senkiben igény mások cselekvésére irányuló kötelezettségek vonatkozóan. És mindezen "hiányok" miatt természetesen a legitimitás kérdése sem vethető fel egyelőre.Direkt reciprocitás játékok
A direkt reciprocitásról akkor beszélhetünk, ha a játékosok ismerik egymást. Kérdés persze, hogy miért is fontos mindez, mit is jelent ez az ismeretség. Amikor ismételt játékokat engedünk meg, akkor azon túl, hogy a modellezni tudjuk a társadalmi emlékezet jelenségét, valami más is lehetővé válik. A játékok ismételhetősége, az a tény, hogy a játékok sorban követik egymást, az teszi lehetővé, hogy a játékosok reagálni tudjanak a másik cselekvésére. Figyelembe vehetik a partnerük múltbeli cselekvéseit (esetleg a sajátjukat is), illetve mérlegelhetik azt is, vajon a jövőben mit lépne a partnerük, ha ők a jelenben így vagy úgy cselekednének. Innentől kezdve a játékosok már alkalmazhatnak feltételes stratégiákat is.| magjátékok | ||||||||||||||
| aszimmetrikus játékok | szimmetrikus | |||||||||||||
| többalternatívás játékok | kétalternatívás | |||||||||||||
| többszereplős játékok | kétszereplős | |||||||||||||
| nem szigorúan rendezett játékok | szigorúan rendezett | |||||||||||||
| aszinkron játékok | szinkron | |||||||||||||
| ismételt játékok | ismételt | |||||||||||||
| direkt reciprocitás játékok | ismerős játékosok | |||||||||||||
| indirekt reciprocitás játékok | ismeretlen játékosok | |||||||||||||
| kooperatív (ígéret) játékok | nem kooperatív (ígéretmentes) | |||||||||||||
Evolúciósan stabil stratégia
A stratégia fogalmát már bemutattam, és a későbbiekben is lesz még róla szó. Az evolúciósan stabil stratégia (Evolutionarily Stable Strategy – ESS) fogalmát azonban még nem vettem tárgyalásba, most viszont megteszem, mert szükségem lesz rá. [♦] A fogalom az evolúciós elméletek területéről szivárgott át a játékelmélet vidékére. [♦] Az evolúciósan stabil stratégia fogalmával speciális minőséget lehet kifejezni a stratégiák egymáshoz való viszonyában. Az evolúcióbiológiától átvehető egyik fontos módszertani eszköz a populációdinamikai modellezés technikája. Ha vizsgálni akarjuk, hogy valamely viselkedésmód, magatartási stratégia hogyan képes elterjedni egy nagyobb populációban, akkor azt úgy tehetjük meg, hogy a "versengő" stratégiákat "szétosztjuk" a különböző csoportok között, és szimulációs számításokat végzünk arra vonatkozóan, hogy a csoportok, egyének interakciói során a különböző stratégiák követése mennyi nyereséget, veszteséget hoz a stratégiákat követő egyének, csoportok számára. A stratégiák sikerességét azzal fejezhetjük ki, hogy a népesség egészében egyre több egyed követi a sikeres viselkedési szabályt. Erre a "kiválasztódási folyamatra" nyugodtan mondhatjuk azt, hogy társadalmi tanulással, nem pedig biológiai kiválasztódással valósul meg. A népesség egészében elterjedni látszó – ebben az értelemben – domináns stratégiák azonban még nem biztos, hogy hosszú ideig képesek lesznek stabilan fennmaradni. Fontos kérdés az, hogy mi történik, ha a populáción belül egy domináns stratégia mellett megjelenik egy másik stratégiát követő csoport. Meg tudja-e az új – mutáns – stratégia ingatni a korábban domináns stratégia helyzetét? Saját magával szemben hogy viselkedik a stratégia, megerősíti-e saját magát, vagy esetleg utat nyit más stratégiák számára, amelyek később "lenyomhatják" őt? Ilyen kérdések merülhetnek fel a domináns stratégiákkal kapcsolatban. Az evolúciósan stabil stratégiák képesek ellenállni az ilyenfajta "támadásoknak", vagyis az adott viselkedési mintázatot tartósan fenn tudják tartani a populáció egészén belül.A négy másodrendű stratégia
Az ismételt játékok modelljében az az egyik döntő mozzanat, hogy megjelenik benne az emlékezet. A feltétel nélküli stratégiák esetében nincs szükség még erre, de a tit-for-tat és a többi feltételes stratégia már az emlékezet segítségével tudja a stratégia feltételét szabályba foglalni. És ha már a modellbe bekerül az emlékezet, akkor megjelenhet, megjelenik a jövő is, hiszen ha megismerem a partnerem stratégiáját, akkor ez alapján saját döntésemet formálhatja a jövőre vonatkozó elvárás is. Axelrod szép kifejezésével élve: a jövő árnyéka visszavetül a jelenre. Nem mindegy azonban, hogy mit veszek figyelembe a múltból. A tit-for-tat arra figyel, hogy a partner mit lépett az előző fordulóban. Ez gazdaságos megoldás, mivel nem kell hozzá sok információt tárolni. Minél több patnerünk lehet, annál fontosabbá válik ez a szempont. Két irányban is tágíthatjuk a megjegyzendő múltbeli információk körét. Egyfelől hátranézhetünk messzebb az időben, vagyis több lépésre visszamenőleg figyelhetjük partnereink cselekedeteit. A tit-for-two-tat stratégia például két forduló adatait jegyzi meg: a partner első dezertálása után még kooperál és "csak" a sorban második dezertálást bünteti megtorlással. A távoli múltba nézés azonban nem igazán terjedt el a szimulációs elemzések világában – vélhetőleg azért, mert minél több lépést kéne megjegyezni a múltból, annál nagyobb memóriaigénnyel járna ez a feladat. Mellesleg ez nem is lenne életszerű, hiszen a való életben sem tartjuk minden partnerünkről számon azt, hogy pontosan mit tett velünk korábban. Sokkal inkább valamiféle általános benyomást alakítunk ki róluk, de ennek figyelembe vétele már a reputációs elméletekhez vezetne el minket, amivel csak a következő fejezetben foglalkozom majd (☜) A memória bővítésének másik útja az lehet, hogy továbbra is megmaradunk az előző forduló adatainál, de nemcsak a partnerünk lépését, hanem a sajátunkat is figyelembe vesszük. A tit-for-tat szabály ezt nem teszi meg, de vannak olyan stratégiák, amelyek figyelnek erre. Ha tudni szeretnénk, hogy a direkt reciprocitás feltételei mellett hány stratégia lehetséges elméletileg és mik ezek, akkor érdemes egy egyszerű formalizmust alkalmazni a stratégiák leírására [SyiHO] Egy cselekvési szabály abból áll, hogy bizonyos feltételekhez kooperálást (C), másokhoz dezertálást (D) ír elő. Ezt kifejezhetjük úgy is, hogy a kooperáláshoz az '1', dezertáláshoz '0' értéket rendeljük. Mivel itt a stratégiákat mindig a játékos és partnere előző fordulóban tett lépései alapján határozhatjuk meg, egy cselekvési szabályt úgy adhatunk meg, hogy az előző forduló négy lehetséges állapotához, a kölcsönös kooperáláshoz (CC) és dezertáláshoz (DD, illetve a két aszimmetrikus cselekvéshez (CD és DC) egy-egy cselekvésértéket rendelünk, vagyis a (CC,CD,DC,DD) állapotsorhoz hozzátesszük a szabály által előírtakat. Ezt 16-féleképpen tehetjük meg, tehát ennyi stratégia létezik, és az egyes stratégiákat a (0,0,0,0), (0,0,0,1), …, (1,1,1,1) számsorozatok valamelyikével reprezentálhatjuk. Nem minden elméletileg lehetséges stratégia "értelmes". Vannak olyanok, amelyek gyakran felbukkannak a szimulációs elemzésekben és, ami fontosabb, a gyakorlati életben. Ilyen a feltétel nélkül kooperáló allC (1,1,1,1), a feltétel nélküli dezertáló allD (0,0,0,0), a véletlen szerint döntő random (0.5, 0.5, 0.5, 0.5) vagy az alternáló Alt (0,0,1,1) stratégia. A stratégiák között előfordulnak olyanok is, amelyek sosem szerepelnek jól a szimulációk során, és a gyakorlati előfordulásuk esélye is kicsi. Ezeknek nevet sem szokás adni, ezért csak a számnégyesükkel hivatkozhatunk rájuk. Ilyen például ez a stratégia: (0,0,0,1). A következő fejezetekben röviden megvizsgálom a négy legfontosabb stratégiát, amelyek valamilyen értelemben sikeresnek mondhatóak a szimulációs számítások és a gyakorlati élet tapasztalatai szerint.Tit-for-tat, a tiszta viszonzó stratégia
A direkt reciprocitás elmélethez kapcsolható stratégiák legismertebb példája, a tit-for-tat a Robert Axelrod által meghirdetett számítógépes torna kapcsán került be a köztudatba. Axelrod nyilt versenyt hirdetett ismételt fogolydilemma játéksorozatban való részvételre. A versenybe benevezett stratégiák (pontosabban a stratégiákat megvalósító számítógépes programok) sok meneten keresztül egymás ellen játszottak, mindenki mindenki ellen megmérkőzött, a játékosok (stratégiák) minden játék után pontokat kaptak, ezeket folyamatosan összesítették, aztán a torna végén győztest hirdettek. A végeredmény mindenkit meglepett. Az általánosnak mondható elvárásokkal szemben, amelyek valamilyen dezertáló jellegű stratégia győzelmét jósolták, a tit-for-tat stratégia lett a torna nyertese, amely viszont tartalmazott kooperatív elemeket is. Mellesleg a tit-for-tat stratégia volt a legegyszerűbb az összes között, hiszen csupán két szabályból áll: A Bibliában is több helyen találhatunk olyan passzusokat, amelyek "ugyanerről beszélnek".
"A ki ember-vért ont, annak vére ember által ontassék ki; …" [Mózes I. 9.6]
"Szemet szemért, fogat fogért, kezet kézért, lábat lábért,
Égetést égetésért, sebet sebért, kéket kékért." [Mózes II. 21.24-25]
"Törést törésért, szemet szemért, fogat fogért; a milyen sérelmet ő ejtett máson, olyan ejtessék rajta is.
A ki barmot üt agyon, fizesse meg azt, de a ki embert üt agyon, halállal lakoljon." [Mózes III. 24.20-21]
"És a bírák vizsgálják meg jól a dolgot, és ha hazug tanú lesz a tanú, a ki hazugságot szólott az ő atyjafia ellen:
Úgy cselekedjetek azzal, a mint ő szándékozott cselekedni az ő atyjafiával. Így tisztítsd ki közüled a gonoszt;
Hogy a kik megmaradnak, hallják meg, és féljenek, és többször ne cselekedjenek te közötted ilyen gonosz dolgot.
Ne nézz reá szánalommal; lelket lélekért, szemet szemért, fogat fogért, kezet kézért, lábat lábért. [Mózes V. 19.18-21]
| 42. | 43. | |
| Barátnak barátja légy, | Barátnak barátja légy, | |
| adományt adománnyal | s barátod barátjának | |
| hálálj híven. | szintén szívese; | |
| Gúnyt fizess meg gúnnyal, | ám aki ellened, | |
| s ne maradj fösvény, | egyetlen hívét | |
| fizetvén gonoszért. | se szíveld soha. |
- barátságos (mert az első menetben kooperál),
- megtorló (mert a dezertálást azonnal megbosszulja),
- megbocsátó (mert a kooperálásra azonnal kooperálással válaszol, bármi is volt azt megelőzően) és
- nem irigy (mert egy játékban sosem győzi le a másikat, maximum annyi pontot szerez, mint a partnere).
| $Ego$ és $Alter$ cselekvései az előző fordulóban | (CC, | CD, | DC, | DD) | ||||||||||
| \multirow{2}{*}{$Ego$ cselekvése az aktuális fordulóban}&(C,&D,&C,&D)\\ | ||||||||||||||
| (1, | 0, | 1, | 0) | |||||||||||
$\concept{TFT}(Ego,t_i) \defi ((\concept{C}(Ego,t_{i- 1}) \to$
$(\concept{D}(Alter,t_{i- 1}) \to \rel{O}\concept{D}(Ego,t_i)) \land (\concept{C}(Alter,t_{i- 1}) \to \rel{O}\concept{C}(Ego,t_i))) $
$\land (\concept{D}(Ego,t_{i- 1}) \to$
$(\concept{D}(Alter,t_{i- 1}) \to \rel{O}\concept{D}(Ego,t_i)) \land (\concept{C}(Alter,t_{i- 1}) \to \rel{O}\concept{C}(Ego,t_i))))$
tit-for-tat (hun) – szemet szemért (hun) – viszonzó stratégia (hun) – tit-for-tat (eng) – TFT (eng)
A formula azt fejezi ki, hogy mit tesz az Ego az i. lépésben. A viszonzó stratégiát két állítással definálhatjuk. Az első lépésben ($t_1$ időpontban) Ego kooperál (C). Ez egy kivételszabály, amit az első fordulóra nézve minden stratégiának tartalmaznia kell. Mivel az összes vizsgált stratégia kooperálással kezd, ezért ennek jelzését (itt is, később is) elhagyom a formulákból. A tit-for-tat szabály a második fordulótól kezdve ($t_i > t_1$) mindig a játékostársa (Alter) előző ($t_{i - 1}$ időpontbeli) lépését ismétli. A tit-for-tat stratégia tehát sikeresnek bizonyult mind a szimulációban, mind a gyakorlatban. A kezdeti ragyogását azonban idővel kissé beárnyékolta az a tény, hogy kiderült, bár a stratégia kollektíve stabil, de evolúciós értelemben már közel sem az [Rober] Ha a hibázás lehetőségét is beépítjük a modellbe, figyelembe vesszük a szimulációk során, akkor a stratégia jóval gyengébben teljesít. Ezt persze tudtuk már jóval a szimulációs számítások előtt is, hiszen a szemet szemért (tit-for-tat) elv kritikája kétezer év óta jól ismert a keresztény kultúrkörön belül. Hiszen a jézusi ki kardot ránt, kard által vész el mondat ugyan egyfelől a negatív reciprocitás tényszerű megállapítás, de másfelől egy figyelmeztetés, normatív felszólítás gesztusa is egyben.
"Szemet szemért-szemért-szemért … ott ér véget, ahol mindenki vak." (Gandhi)
"A szemet szemért ősi törvénye mindenkit vakon hagy." (Martin Luther King Jr.)
Bűnbánó stratégia
Ha aszinkron játékokból képezünk játéksorozatot, akkor meglehetősen sikeres stratégiának bizonyul a szigorú, de igazságos (firm-but-fair – FBF) szabály) [Marcu] Bár a 'szigorú, de igazságos' kifejezést a magyar közgondolkodás is ismeri, alkalmazza, mégis úgy gondolom, hogy jobban járunk, ha a bűnbánó stratégia (contrite tit-for-tat strategy) kifejezést használjuk helyette. Az FBF stratégia erősen kooperatív, mert csak egy esetben dezertál: ha az előző menetben a játékos kooperált, miközben a partnere dezertált. Ezt úgy értelmezhetjük, hogy nem is annyira a nagylelkűség, mint inkább a "bűnbánás" a stratégia igazi sajátossága, hiszen ha a játékos korábban dezertált, utána mindkét esetben kooperál (mintegy megbánva korábbi "bűneit"). A tit-for-tat stratégiától a kétszeres dezertálásra való reakcióban tér el azzal, hogy a bűnbánó ekkor kooperál, míg a tit-for-tat dezertál. A tit-for-tat szabály a partner minden dezertálását bünteti, ám a bűnbánó stratégia nem. A kölcsönös dezertálás helyzetét már "szégyenli" (hiszen ő is dezertált), ezért próbálja azt "kijavítani" a kooperálással. A bűnbánó stratégia táblázata a következő.| $Ego$ és $Alter$ cselekvései az előző fordulóban | (CC, | CD, | DC, | DD) | ||||||||||
| \multirow{2}{*}{$Ego$ cselekvése az aktuális fordulóban}&(C,&D,&C,&C)\\ | ||||||||||||||
| (1, | 0, | 1, | 1) | |||||||||||
$\concept{CTFT}(Ego,t_i) \defi ((\concept{C}(Ego,t_{i- 1}) \to$
$(\concept{D}(Alter,t_{i- 1}) \to \rel{O}\concept{D}(Ego,t_i)) \land (\concept{C}(Alter,t_{i- 1}) \to \rel{O}\concept{C}(Ego,t_i))) $
$(\land \concept{D}(Ego,t_{i- 1}) \to$
$\rel{O}\concept{C}(Ego,t_i)))$
bűnbánó stratégia (hun) – szigorú, de igazságos (hun) – contrite TFT (eng) – Firm-But-Fair (eng) – FBF (eng)
A formulából elhagytam az első forduló kivételszabályát (Ego $t_i=t_1$ esetén kooperál), így a fenti két részformula az összes többi fordulóban érvényes előírást rögzíti. Az egyik részformula írja le azt a részszabályt, hogy amennyiben az előző fordulóban ($t_i=t_{i - 1}$) az Ego kooperált (C), akkor az i. menetben a partnere (Alter) előző lépését ismétli. A másik összetevőben pedig az szerepel, hogy amennyiben az Ego az előző fordulóban dezertált (D), akkor most kooperálnia kell (C). Meg kell még itt jegyezzem, hogy amikor Frean bevezette az FBF-stratégiát, akkor a zajos játékokhoz igazodó sztochasztikus stratégiát tervezett, így a kétszeres dezertálás esetében nem a biztos, csak a nagyon valószínű kooperálást írta elő, amit ezzel a mintázattal fejezhetünk ki: (1,0,1,p). Az eddig elmondottak logikája és érvényessége azonban nem változik meg amiatt, hogy a bűnbánó stratégiát a FBF-szabály determinisztikus változataként értelmezem. Érdemes még ehhez azt is hozzátenni, hogy ugyanez a cselekvési szabály felbukkan a bűnbánó tit-for-tat (contrite TFT) [boyd:] valamint a hírnévápoló (Standing) stratégia név alatt is [sugde] Ezekkel azért nem foglalkozom itt, mert mindkettő stratégia az indirekt reciprocitás körébe tartozik.Számító stratégia
Ahogy Axelrod tornáján Anatol Rapoport pszichológus volt az, aki beküldte a nyertes tit-for-tat programot, úgy az ő nevéhez köthető annak a stratégiának az első megfogalmazása is, amit együgyű (Simpleton) stratégiának nevezett el [Ridle] Ez a stratégia később más neveket is kapott, és inkább ezek terjedtek el szélesebb körben. A nyer-marad-veszít-vált (angolul win-stay-lose-shift – WSLS) stratégia [nowak] valamint a Pavlov megnevezések [krain] [krain] egyaránt a Rapoport-féle együgyű stratégiának felelnek meg, aminek lényegét a Győztes csapaton ne változtass! mondás fejezi ki a legjobban. Ez a szabály a kölcsönösség után vagyis a szimetrikus cselekvések esetén (CC és DD) kooperál, aszimmetrikus helyzetekben (CD és DC) dezertál, amit így írhatunk fel.| $Ego$ és $Alter$ cselekvései az előző fordulóban | (CC, | CD, | DC, | DD) | ||||||||||
| \multirow{2}{*}{$Ego$ cselekvése az aktuális fordulóban}&(C,&D,&D,&C)\\ | ||||||||||||||
| (1, | 0, | 0, | 1) | |||||||||||
$\concept{PAVLOV}(Ego,t_i) \defi ((\concept{C}(Ego,t_{i- 1}) \to$
$(\concept{D}(Alter,t_{i- 1}) \to \rel{O}\concept{D}(Ego,t_i)) \land (\concept{C}(Alter,t_{i- 1}) \to \rel{O}\concept{C}(Ego,t_i))) $
$\land (\concept{D}(Ego,t_{i- 1}) \to$
$(\concept{C}(Alter,t_{i- 1}) \to \rel{O}\concept{D}(Ego,t_i)) \land (\concept{C}(Alter,t_{i- 1}) \to \rel{O}\concept{D}(Ego,t_i))))$
számító (hun) – győztes csapaton ne változtass (hun) – Win-Stay-Lose-Shift (eng) – Simpleton (eng) – WSLS (eng) – Pavlov (eng)
A formulából az első forduló kivételszabályát (Ego kooperál) elhagytam. Az első részformula szerint, amennyiben az előző fordulóban ($t_i=t_{i - 1}$) az Ego kooperált (C), akkor az i. menetben a partnere (Alter) előző lépését ismétli. A második részformulában pedig az szerepel, hogy amennyiben az Ego az előző fordulóban dezertált (D), akkor a jelenlegiben pont az ellenkezőjét csinálja annak, mint amit az Alter csinált az előzó menetben. [♦] Ez a szabály tanuló stratégia, mivel az előző forduló tapasztalatait értékelve alakítja ki az aktuális lépését. Mivel a szabály arra figyel, hogy mindig a legtöbb pontszámot érje el, ezért a számító stratégia megnevezés tűnik számára a legmegfelelőbbnek, de használni fogom a Pavlov nevet is. Ez a stratégia is akkor igazán sikeres, ha a tit-for-tat játékosok előzőleg megtisztítják a terepet az önző allD stratégiáktól [Ridle]Haragtartó stratégia
Az elemzésekben időről időre felbukkan a Grim trigger (GT) stratégia [James] amit haragtartó, engesztelhetetlen, zord vagy zordra váltó stratégiának fordíthatnánk (Axelrod 1984-es könyvében ezt Friedman stratégiának nevezi [axelr] Ez a cselekvési mintázat barátságosan kezd, és mindaddig kooperál, amíg a másik is ezt teszi, de a partner első dezertálása után ő is azonnal dezertálásba vált, és attól kezdve már sosem tér vissza a kooperáláshoz. Ez a stratégia engesztelhetetlenül haragtartó, sosem bocsát meg. Azok, akik ezt a stratégiát javasolják, az tartják az előnyének, hogy nagy a visszatartó ereje, hiszen a kooperálás feladását az örökös dezertálással fenyegeti, vagyis a legerősebb büntetést helyezi kilátásba. A haragtartó stratégiára a következő mintázat jellemző.| $Ego$ és $Alter$ cselekvései az előző fordulóban | (CC, | CD, | DC, | DD) | ||||||||||
| \multirow{2}{*}{$Ego$ cselekvése az aktuális fordulóban}&(C,&D,&D,&D)\\ | ||||||||||||||
| (1, | 0, | 0, | 0) | |||||||||||
$\concept{GT}(Ego,t_i) \defi ((\concept{C}(Ego,t_{i- 1}) \to$ $(\concept{D}(Alter,t_{i- 1}) \to \rel{O}\concept{D}(Ego,t_i)) \land (\concept{C}(Alter,t_{i- 1}) \to\\ \rel{O}\concept{C}(Ego,t_i)))$ $\land (\concept{D}(Ego,t_{i- 1}) \to \rel{O}\concept{D}(Ego,t_i)))$
haragtartó (hun) – Grim Trigger (eng) – Friedman (eng)
Az első forduló kooperálási szabályát itt is kihagytam. Az első részformula szerint Ego előző fordulóbeli kooperálása esetén az aktuális fordulóban megismétli a partnere (Alter) előző lépését. A második összetevő pedig azt írja le, hogy amennyiben az Ego az előző fordulóban dezertált (D), akkor most is dezertálni fog (D) függetlenül attól, mit tett korábban a partnere. A szimulációs eredmények azt mutatják, hogy ez a stratégia sosem tud igazán jól szerepelni, mert nagyon könnyen keveredik megtorlási spirálba [Rober] Különösen így van ez zajos játékokban.A négy alapstratégia
Ez eddig bemutatott stratégiák mind olyanok voltak, hogy a szimulációs számítások és a gyakorlati tapasztalat szerint is a sikeres, bizonyos feltételek mentén gyakran alkalmazott cselekvési szabályoknak lehet minősíteni őket. Talán csak a haragtartó (Grim trigger) stratégia volt az, amire kevesebbszer hivatkoztak mint kooperációkész szabályra a többi háromhoz képest. A bemutatott stratégiáknak van egy érdekes közös vonása, ami talán nem véletlen. Mind a négy szabály megegyezik abban, hogy mit ír elő azután, hogy a játékos kooperált az előző fordulóban (mondhatjuk erre, hogy a játékos jó volt):- kooperál, ha a partnere kooperált,
- dezertál, ha a partnere dezertált.
| (CC, | CD, | DC, | DD) | |||||||||||
| viszonzó | TFT | (1, | 0, | 1, | 0) | |||||||||
| bűnbánó | FBF | (1, | 0, | 1, | 1) | |||||||||
| számító | WSLS | (1, | 0, | 0, | 1) | |||||||||
| haragtartó | GT | (1, | 0, | 0, | 0) | |||||||||
Társadalmi hiba – zajos játékok
Az előző fejezetekben megírtam, hogy az ismételt fogolydilemma játék (Iterated Prisoner's Dilemma Game – IPDG) bevezetésével modellezni tudjuk a társadalmi emlékezetet és ezzel a cselekvéseink viszonzási rendszeren keresztüli összekapcsolását. Az egymásra hivatkozó, egymásba kapcsolódó cselekvési láncok megfelelő stratégiák követésével alakíthatók ki és tarthatók fenn. Ezen stratégiák között a legismertebb a tit-for-tat szabály, aminek megtalálhatjuk a nyomát minden kultúrában. És – legalább a keresztény-zsidó kultúrából – ismert a tit-for-tat stratégia talán legfontosabb hátránya is: a szemet szemért elv könnyen "rálöki" az embert a megtorlási spirál pályájára. A történelem, a mindennapi élet tapasztalatai azt mutatják, hogy ha mindig a tit-for-tat szabályhoz ragaszkodnánk mereven, akkor egyetlen tévedés, kicsiny kis hiba is elegendő lenne ahhoz, hogy az egymásra feleselő cselekvések a dezertálási-büntetési ágra váltsanak át (vagyis a megtorlási spirálba keveredjenek bele). Axelrod tornájával szemben elég hamar megfogalmazták azt a kritikát, hogy ebből a szempontból nézve súlyos deficittel küzd, mivel nem képes kezelni a társadalmi hibázás lehetőségét. A számítógépes programok sosem hibáznak. Az éppen adott szabályt minden lépésben pontosan végrehajtják. Ebben az értelemben nagyon sterilek, és nem képesek modellezni azt a tényt, hogy a valós emberek – bár sokszor követnek valamely stratégiát – néha eltérnek a cselekvési szabály előírásaitól. Többféle oka is lehet ennek. Lehetséges, hogy a cselekvő maga téveszt, és eltér a szabály által előírtaktól. Ilyenkor – Reinhard Selten szép kifejezésével élve – a remegő kéz (trembling hand) jelenségéről beszélhetünk. De előfordulhat az is, hogy mások hibáznak abban az értelemben, hogy félreértik (akaratlanul vagy akarattal) a cselekvésünket. A téves percepció (fuzzy mind) ugyanúgy befolyással lehet a játéksorozat kimenetére, hiszen végülis az a fontos, hogy a játékosok mit észlelnek egymás cselekvéseiből (nem pedig az, hogy ténylegesen mi történik). A számítógépes szimuláció során a tit-for-tat stratégia sosem kerülhet megtorlási spirálba, míg a valós életben egy ember, aki általában követi a tit-for-tat szabályt, olykor mást léphet, mint amit a szabály szerint éppen lépnie kellene. Ezt a hibázási lehetőséget a játékelméleti modellekbe úgy "vehetjük fel", hogy bevezetjük a zajos játékok fogalmát [DrewF] Ez annyit jelent, hogy amikor az egyes stratégiákat követő játékosok közöti játéksorozatot szimuláljuk, akkor a bizonyos valószínűség mellett – mintegy "kívülről beavatkozva" –megváltoztatjuk egy-egy lépés tartalmát (tehát ha valakiken kooperálnia kéne, a lépését dezertálásra váltjuk, és fordítva). Ezzel beviszünk egy hibázási faktort a rendszerbe, és a nagy kérdés az lesz, vajon milyen stratégiák lesznek sikeresek ilyen feltételek között. A válasz tulajdonképpen nem meglepő. Olyan stratégiák képesek kezelni a megváltozott – tegyük hozzá: a valóságot jobban modellező – helyzeteket, amelyek egyrészt jóindulatúbbak a tit-for-tat stratégiához képest, másrészt tanulni képesek a múlt – jó és rossz – döntéseiből. Az előzőre a nagylelkű tit-for-tat (Generous Tit-For-Tat – GTFT) szabály a példa [nowak] az utóbbira a pavlovi ("győztes csapaton ne változtass" elvet megvalósító) stratégia [nowak] A GTFT-t azért mondják nagylelkű tit-for-tat szabálynak, mert – a stratégia követésébe egy belső valószínűségi változót csempészve – bizonyos pontokon, amikor dezertálnia kellene az előírás szerint, mégis kooperál. Néha nagylelkűen "elnézi" a partner dezertálását. Ez a szabálymódosítás elég lehet ahhoz, hogy a társadalmi hiba miatt beinduló - és egyébként végtelenné váló – megtorlási spirált meg lehessen szakítani, és vissza lehessen téríteni a kooperálási ágra a játék menetét. A Pavlov stratégiát már bemutattam korábban, a szabály logikáját az ott leírtak alapján lehet megérteni (☜)A játékok közösségi kiterjesztése reputációval
Említettem, hogy a direkt reciprocitás jelensége csak kis létszámú társadalmakban működik, hiszen az a feltétel, hogy a résztvevőknek ismerniük kell egymást, nem enged meg nagyobb létszámot. Viszont a helyi közösségek növekedés sok helyen nagyobb létszámú társdalmakat eredményezett, ám ezekben a társadalmakban is megtalálhatóak a kooperáció mintázatai, itt is van reciprocitás. A kérdés az, hogy miként, milyen formában, miért alakulnak ki mindezek? A társadalmi modellünket ezen a ponton újra csak bővítenünk kell, mégpedig egy nagyon fontos társadalmi intézményt kell felvennünk: a reputáció mint társadalmi értékelés jelenségét. Ahhoz pedig, hogy ezt modellezni tudjuk, szükségünk lesz arra, hogy a 'közösséget' mint az értékelést végző új "szereplőt" is felvegyük a modellbe a játékosok mellé.Indirekt reciprocitás játékok
A direkt reciprocitás jelensége kialakítható és fenntartható azzal, hogy kooperálás és dezertálás (büntetés) valamilyen egyvelegéből kialakított stratégiát érvényesítünk. Az ilyen feltételes stratégiák azonban csak akkor és azon az alapon működnek, ha feltesszük, hogy a játékosok ismerik egymást. A kooperációt azonban megtalálhatjuk olyan ismétlődő társadalmi helyzetekben is, amelyekben idegenek kerülnek kapcsolatba egymással. Meg kell tudnunk magyarázni az olyan eseteket is, amikor a játékok ismétlődnek, de a játékosok ismeretlenek egymás számára. Az ilyen helyzeteket nevezzük indirekt reciprocitásnak.| magjátékok | ||||||||||||||
| aszimmetrikus játékok | szimmetrikus | |||||||||||||
| többalternatívás játékok | kétalternatívás | |||||||||||||
| többszereplős játékok | kétszereplős | |||||||||||||
| nem szigorúan rendezett játékok | szigorúan rendezett | |||||||||||||
| aszinkron játékok | szinkron | |||||||||||||
| ismételt játékok | ismételt | |||||||||||||
| direkt reciprocitás játékok | ismerős játékosok | |||||||||||||
| indirekt reciprocitás játékok | ismeretlen játékosok | |||||||||||||
| kooperatív (ígéret) játékok | nem kooperatív (ígéretmentes) | |||||||||||||
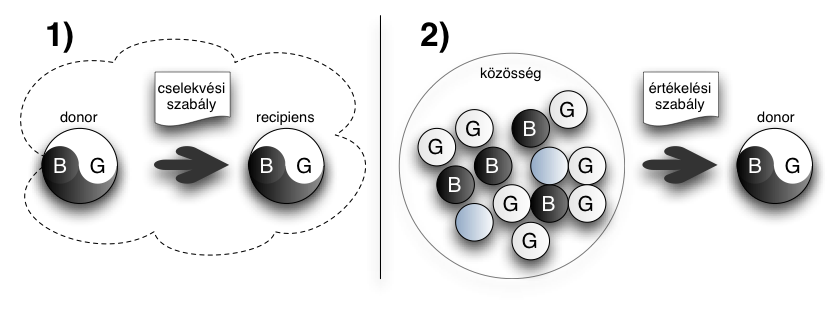
Az indirekt reciprocitás stratégiafogalmát kiterjesztve mindig tudnunk kell, hogy milyen viselkedési szabály szerint dönt a Donor, illetve milyen értékelési rendszer alapján értékeli (újra) a Donor reputációját a közösség a Donor cselekvése alapján. A cselekvési szabályokról bővebben írtam másutt, itt elegendőnek tartom hivatkozni az ott leírtakra [syiDi] Az értékelési mechanizmusokat viszont itt kell bemutatnom, úgyhogy a következőkben röviden áttekintem a legfontosabb reputációs rendszereket. Első körben a négy másodrendű értékelési rendszert veszem sorba, majd utána bemutatom azt, hogy a harmadrendű értékelési rendszereket hogyan lehet modellezni a már ismert másodrendű rendszerek segítségével. A másodrendű értékelési szabály fogalma azt jelenti, hogy az értékelés során két dolgot veszünk figyelembe: a Donor cselekvését, illetve a Recipiens reputációját. A harmadrendű értékelés ezeken felül figyel a Donor reputációjára is [syiDi] Az indirekt reciprocitás, a reputáció típusainak megragadásához további formulákat kell felvennünk a formális modellünkbe. Valamilyen logikai elemmel meg kell tudnunk ragadni a reputáció, vagyis a közösségi értékelés jelenségét. Erre a célra alkalmas lehet egy $\rel{A}$ deontikus operátor felvétele a leíró nyelvünkbe, amivel – a már ismert $value(agent, t_i)$ értékelési függvényünkkel együtt – kifejezhetjük azt, hogy egy értékelési szabály szerint jó és rossz minősítést (reputációt) kell kiosztani az ágensekre. [♦]
$\rel{A}\{\concept{VALUE}(agent, t_i) = Bad\}$
ágens rossz reputációja (hun) – bad reputation of agent (eng)
$\rel{A}\{\concept{VALUE}(agent, t_i) = Good\}$
ágens jó reputációja (hun) – good reputation of agent (eng)
A Donor saját cselekvési szabálya szerint cselekszik, ami a most vizsgált esetekben mindvégig egy nagyon egyszerű, másodrendű szabály lesz. A diszriminatív kooperálás (Disc:Co) stratégiáját fogja az összes vizsgált módszer alkalmazni (a jó Recipienssel szemben kooperál, a rossz partnerrel szemben dezertál). [♦] Az értékelő közösség saját reputációs szabálya szerint ítéli meg a Donor aktuális cselekvését, és nyilván különbözni fognak egymástól a most bemutatandó értékelési módszerek. Egy valamit kell még tisztázni, mielőtt a reputációs szabályok bemutatásába kezdenék: meg kell adni, hogyan lehet összekapcsolni a cselekvéseket és az értékeléseket egymással. Ezt a következő szabállyal (formulával) fejezhetjük ki.$\concept{DO}(Ego,a,t_i) \to \concept{VALUE}(Ego,t_i)=\concept{VALUE}(a,t_i)$
a cselekvés és értékelés összekapcsolása (hun) – connection of action and assessment (eng)
Ez a formula azon az alapon teremti meg a kapcsolatot a cselekvés és az ágensek minősítése között, hogy a cselekvésekre, illetve ágensekre vonatkozó értékelés valenciája megegyezik (például a kooperációra mint cselekvésre és a jó cselekvőre mint ágensre irányuló értékelés valaencája mindkét esetben pozitív).Kép-mutató (Image Scoring) értékelési rendszer
Az indirekt reciprocitás első elmélete az Image Scoring módszertant mutatta be, mint a reputációs rendszerek prototípusát [nowak] Szigorú módszertani szempontok szerint ez az értékelési rendszer nem is másod-, hanem elsőrendű, de ez nem változtat azon a tényen, hogy ebben a minőségében is az elméletileg lehetséges négy másodrendű értékelési rendszer egyik típusát jelenti.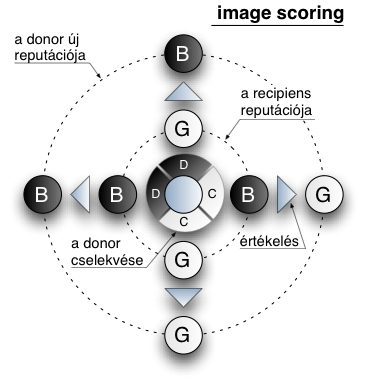
A többihez hasonlóan ez a módszertan is azzal indít, hogy mindenkinek 'jó' minősítése van a játékban. A cselekvési szabály a már említett diszkrimanítív kooperálás szabálya: Jóval szemben kooperálni, Rosszal szemben dezertáni kell. Az Image scoring módszer lényege az, hogy minden egyes döntés után a Donor reputációja, képe (imidzse) aszerint változik, hogy segítette-e a Recipienst vagy nem. Ha a Donor kooperált, vagyis segített, akkor onnantól Jó lesz (akármi is volt addig), dezertálása esetén pedig, vagyis amikor nem segített, a Donor rossz minősítést kap (akármi is volt addig a reputációja).
Az első reputációs elméletről szóló cikkben a szerzők (Nowak és Sigmund) azt hozták ki, hogy ez a módszertan képes stabil kooperációt kialakítani egy közösségen belül, de a későbbi szimulációs számítások árnyaltak ezen a képen. Egyesek olyan – katalizáló – szerepet tulajdonítanak ennek a stratégiának, mint amilyet szerepet a TFT-stratégia tölt be a direkt reciprocitást szimuláló modellekben
[nowak]
Mindenesetre születtek később olyan publikációk is, amelyek az Image Scoring módszer tényleges érvényesülését mutatták ki az állatvilág bizonyos szegmenseiben.
[♦]
A módszer formális reprezentációja.
$\concept{IS}(Ego,t_i) \defi ($
$(\concept{G}(Alter,t_i) \to \rel{A}\{\concept{DO}(Ego,a,t_i) \to \concept{VALUE}(Ego,t_i)=\concept{VALUE}(a,t_i)\}) \land (\concept{B}(Alter,t_i) \to $
$\rel{A}\{\concept{DO}(Ego,a,t_i) \to \concept{VALUE}(Ego,t_i)=\concept{VALUE}(a,t_i)\}))$
kép-mutató (hun) – Image Scoring (eng)
Az Image Scoring módszert nemcsak azzal támadták később, hogy sok esetben nem képes a kooperáció tartós kialakítására, de "érték" alapon is kritizálták sokan. Ez a módszer ugyanis "érzéketlen" a Recipiens reputációjára. [♦] Márpedig – szóltak az ellenérvek – ha nem segít valaki a Recipiensnek, az nem feltétlen jelent rosszat, amiért a Donort reputációját "le kéne húzni". Mert mi van akkor, ha a Donor büntetésből nem segít a rossz Recipiensnek. E kérdésből kiindulva kezdtek el keresni további értékelési rendszereket.Egyszerű hírnévápoló (Simple Standing) értékelési rendszer
A Simple Standing értékelési rendszer abban tér el az Image Scoring módszertől, hogy a rossz Recipienssel szemben megengedi a büntetést. Ez abban nyilvánul meg, hogy ha a Donor egy rossz Recipiensnek nem segít (büntetésből), akkor ezt a Simple Standing módszer helyesli és a Donort ezek után Jó minősítéssel látja el.
Ez a módszertan az egyik legtöbbet sulykolt értékelési rendszert modellezi a valós társadalmi gyakorlatunkból. A gyerekeinket úgy neveljük fel, és felnőttkorunkban is ezerszer kerülünk olyan helyzetbe, hogy elmondjuk azt a mondatot (magunknak, másoknak), amely a Simple Standing módszertant megalapozó elvnek tekinthető:
A büntetés igazolását adja meg ez az értékelési rendszer, ezért olyan fontos. A mindennapi narratíváink egyik legfontosabb összetevője ez az elv. Ezáltal tudjuk nagy létszámú társadalmakban is fenntartani a kooperációs mintákat, mert lehetővé teszi a büntetés intézményét az ismeretlenekkel, idegenekkel szemben úgy, hogy a büntetésben megnyilvánuló – elsőrendű – dezertálást társadalmilag igazoltnak, megengedhetőnek minősítsük.
[♦]
Ez a stratégia a Standing metódus másodrendű változata
[ohtsu]
[ohtsu]
[Ohtsu]
A különbség köztük abban van, hogy ez az egyszerűsített változat jónak minősíti a rossz személy visszautasítását akkor is, ha a Donor maga előtte rossz volt (az eredeti hírnév-gyűjtő stratégia ezt a diszkriminációt csak a jó Donorokkal szemben alkalmazta). Ez annyit jelent, hogy ez a szabály jónak tartja azt is, ha a hipokrita játékos bünteti a Rosszat. A másodrendű változat alkalmazásának "célja" az értékelési feladat egyszerűsítése lehet, hiszen ebben az esetben kevesebb információt kell beszerezni és feldolgozni. A szabály formulája a következő.
$\concept{SS}(Ego,t_i) \defi ((\concept{G}(Alter,t_i) \to \rel{A}\{\concept{DO}(Ego,a,t_i) \to $
$\concept{VALUE}(Ego,t_i)=\concept{VALUE}(a,t_i)\}) \land (\concept{B}(Alter,t_i) \to$
$ \rel{A}\{\concept{G}(Ego,t_i)\}))$
egyszerű hírnévápoló (hun) – Simple Standing (eng)
A Simple Standing értékelési módszer lényege az, hogy "bevezeti" a büntetés intézményét. Ebben azonban nem még csak az első lépést teszi meg, hiszen ez a stratégia azzal ismeri el a büntetést, hogy jutalmazza azokat, akik megbüntették a Rosszakat. Kitart viszont azon értékelés mellett, hogy a kooperáció feltétlen jó dolog, ha tehát valaki kooperál, akkor őt mindenképpen jónak kell minősíteni.Kérlelhetetlen (Stern Judging) értékelési rendszer
A kérlelhetetlen (Stern Judging) értékelési rendszer még egy lépést tesz a büntetés irányába a Simple Standing módszertanhoz képest. Az utóbbi ugyanis egy ponton még "elnéző" a Rosszakkal szemben, és ezen a ponton lehet még szigorítani a rossz Recipiensekkel szembeni fellépésen.
A Stern Judging
[pache]
megegyezik egy jóval korábban megfogalmazott elképzeléssel, amit kandori-módszernek neveztek el
[kando]
A stratégia két alszabályból áll:
- (i)] nő a Donor reputációja, ha segíti a Jót és nem segíti a Rosszat, illetve
- (ii)] csökken a Donor reputációja, ha segíti a Rosszat és visszautasítja a Jó támogatását.
$\concept{SJ}(Ego,t_i) \defi ((\concept{G}(Alter,t_i) \to \rel{A}\{\concept{DO}(Ego,a,t_i)$
$ \to \concept{VALUE}(Ego,t_i)=\concept{VALUE}(a,t_i)\}) \land (\concept{B}(Alter,t_i) \to$
$ \rel{A}\{\concept{DO}(Ego,a,t_i) \to \concept{VALUE}(Ego,t_i)\ne \concept{VALUE}(a,t_i)\}))$
kérlelhetetlen (hun) – Stern Judging (eng)
Jól látszik az értékelési szabály formuláján, hogy mindkét feltétel (jó vagy rossz Recipiens) esetén reciprok módon alakul ki a Donor új reputációja, csak amíg a jó Recipienssel szemben az új reputáció megegyezik, addig a Rossz esetében ellentétes lesz a Donor cselekvésének értékelésével.Elkerülő (shuning) értékelési rendszer
A Shunning értékelési rendszer próbálja még tovább növelni a "büntetési faktort", ami első pillanatra talán nehezebben vehető észre, ha a módszertan ábrájára tekintünk, mert a Stern Judging módszertanhoz képest annyi a változás benne, hogy a Rosszal szemben alkalmazott büntetést (nem segítést) most rossznak minősíti (ezzel "törli" a Simple Standing módszer által bevezetett szabályt a rossz megbüntetésének helyességére vonatkozóan). A módszertan kevesebb figyelmet kapott a többi három másodrendű értékelési rendszerhez képest, pedig fontos társadalmi jelenség modellezésére alkalmas [panch] [takah] [Ohtsu] A Shunning stratégia logikája (két alszabálya) a következő:- (i)] mindig bünteti a dezertálást és
- (ii)] minden esetben bünteti a Donort, ha az rossz személlyel kerül kapcsolatba – még akkor is, ha egyébként a Donor segíti a Recipienst
A módszer névválasztásával azt akarták kifejezni, hogy a stratégia a Rosszak kizárására, elkerülésére ösztönözhet, mivel a velük kapcsolatos bármilyen érintkezés "káros" lehet a Donor számára. Első hallásra talán meglepő, nehezebben értelmezhető, elfogadható ez az értékelési módszer, pedig a Rosszakkal való érintkezés büntetése meglehetősen gyakran előfordult a történelemben
[syiDi]
és nyilván a jövőben is találkozni fogunk ezzel a jelenséggel. Ez az értékelési rendszer a kizárásra törekvő, a szegregációs szándékok mélyén meghúzódó logika. Vannak társadalmi állapotok, amikor társadalmi csoportok között túl naggyá válnak a társadalmi, kulturális távolságok, és elérkezhet egy pillanat, amikortól az egyik közösség hirtelen átvált a Shunning módszertanra, mert a közösségközi konfliktusokat úgy vélik feloldhatónak, ha a két közösséget teljesen elszeparálják egymástól. Ilyenkor veszik elő ezt a módszertant. A szimulációs számítások ezt az értékelési rendszert kooperációs minták kihordására többnyire alkalmatlannak szokták minősíteni, és a történelmi tapasztalatok sem igazán arról szólnak, hogy a szegregáció képes lett volna megoldani a közösségközi konfliktusokat. Formulája a következő.
$\concept{SH}(Ego,t_i) \defi ((\concept{G}(Alter,t_i) \to $
$\rel{A}\{\concept{DO}(Ego,a,t_i) \to \concept{VALUE}(Ego,t_i)=\concept{VALUE}(a,t_i)\}) \land (\concept{B}(Alter,t_i) \to $
$\rel{A}\{\concept{B}(Ego,t_i)\}))$
elkerülő (hun) – Shunning (eng)
A kirekesztés, a szegregáció szabályának formuláján érezni a Rossz dominanciáját, hiszen a jó Recipiens esetén a reputációs értékelés megyezik a cselekvés értékvalenciájával, ám a Rossz partnerrel szemben csak rossz minősítést lehet kapni (bármit is tegyen az ember).A négy értékelési szabály áttekintése
Az értékelési szabályok bemutatása után érdemes egyetlen táblázatba rendezni őket, hogy jobban szembetűnővé válhassanak a köztük levő hasonlóságok és különbségek.| \multirow{2}{*}{értékelési szabály $\downarrow$}&$\concept{value'}(Alter,t_{i})\rightarrow$&\multicolumn{2}{c}{G}&\multicolumn{2}{c}{B}\\ | ||||||||||||||
| $do'(Ego,t_{i})\rightarrow$ | C | D | C | D | ||||||||||
| Image Scoring&\multirow{4}{*}{$\concept{value'}(Ego,t_{i})\rightrightarrows$}&G&B&G&B\\ | ||||||||||||||
| Simple Standing | G | B | G | G | ||||||||||
| Stern Judging | G | B | B | G | ||||||||||
| Shunning | G | B | B | B | ||||||||||
Harmadrendű stratégiák dekomponálása
A stabil kooperációképes másodrendű stratégiákat még inkább fontosnak tarthatjuk, ha felismerjük, hogy a sikeres harmadrendű stratégiák mind visszavezethetőek a most tárgyalt másodrendű stratégiákra [syiDi] Elméletileg 4096 harmadrendű stratégia létezik, és ebből összesen nyolc olyan van, amely kooperáció kialakítására és fenntartására képes. Ám ezek – egy egyszerű dekomponálási technika alkalmazásával – könnyen értelmezhetőek a korábban elemzett négy másodrendű értékelési szabály és egy-egy egyszerű cselekvési szabály kompozíciójaként.A direkt és indirekt reciprocitás közös mintázatai
Korábban bemutattam, hogy mind a direkt, mind az indirekt reciprocitás feltételei közt négy-négy másodrendű stratégia (cselekvési, illetve értékelési szabály) képes valamilyen formában és mértékben hozájárulni a kooperáció kialakulásához. A stratégiákhoz rendelt formulák hasonlósága alapján a cselekvési és értékelési szabályok párba kapcsolhatók egymással. Az egyszerű TFT és az Image Scoring, a bűnbánó és a Simple Standing, a Pavlov és a Stern Judging, valamint a haragtartó és a Shunning szabályok ugyanazt a mintázatot mutatják, logikájukat tekintve hasonlóképpen működnek [Rosas] Ha a direkt reciprocitáshoz tartozó stratégiák esetén a feltételes cselekevési szabályokban kicseréljük a kooperálásra, illetve dezertálásra utaló C, illetve D jelzéseket 1, illetve 0 értékekre, valamint az indirekt reciprocitás értékelési szabályait összegző táblában szereplő G, illetve B jelek helyett szintén 1, illetve 0 értékeket írunk, akkor a kétféle szabálynégyest egy táblában reprezentálhatjuk.| \multirow{2}{*}{ACRs $\downarrow$}&\multicolumn{2}{c}{C}&\multicolumn{2}{c}{D}&$\leftarrow\concept{do'}(Ego,t_{i \minus 1})$\\ | ||||||||||||||
| C | D | C | D | $\leftarrowdo'(Alter,t_{i - 1})$ | ||||||||||
| Simple TFT | 1 | 0 | 1 | 0 | Image Scoring | |||||||||
| Contrite TFT | 1 | 0 | 1 | 1 | Simple Standing | |||||||||
| Pavlov | 1 | 0 | 0 | 1 | Stern Judging | |||||||||
| Grim Tigger | 1 | 0 | 0 | 0 | Shunning | |||||||||
| $\concept{do'}(Ego,t_{i})\rightarrow$&C&D&C&D&\multirow{2}{*}{$\uparrow$ ASRs}\\ | ||||||||||||||
| $\concept{value'}(Alter,t_{i})\rightarrow$\multirow{2}{*}{}&\multicolumn{2}{c}{G}&\multicolumn{2}{c}{B}&\\ | ||||||||||||||
"Úgy véljük, hogy a Scoring szerepe az indirekt reciprocitásban hasonló, mint a Tit-for-tat szabályé a direkt reciprocitáson belül. Egyik stratégia sem evolucionárisan stabil, de az a képességük, hogy katalizálják a kooperáció kialakulását kedvezőtlen körülmények között, valamint az egyszerűségük jelentőséget kölcsönöz nekik." [nowak]
Mindkét szabály "ellenzi" a büntetést, bár ezt hipokrita módon teszik. Közös elvük az, hogy nem fogadják el büntetést, tehát ha valaki büntet, akkor azt büntetik: 'büntesd, aki büntet'. Amikor Sugden 1986-ben javasolta saját $T_1$ módszerét (a Standing szabályt) [sugde] akkor ő nem beszélt reputációról, bár ahhoz közel álló fogalmat használt: 'kiállás' ('standing'). Sugden nem igazán reflektált a kérdésre, de tény, hogy cselekvési és nem értékelési szabályokról beszélt. Jóval később Sugden szabálya Standing (Simple Standing) néven mint értékelési szabály az indirect reciprocitás elméletek részévé vált. Amikor 1989-ben Boyd újracímkézte Sugden szabályát bűnbánó tit-for-tat stratégiának [boyd:] akkor ő is cselekvési szabályként hivatkozott rá. Ez a kettős kezelésmód persze valamiféle terminológiai zavar, fogalmi pongyolaság jele, de mindebben az a fontos most, hogy ez az "összemosás" nem véletlen. Az összekeverhetőség ugyanis a bűnbánó és a Simple Standing szabályok közötti szoros kapcsolatot jelzi. Amikor Frean bevezette a szigorú, de igazságos Firm-But-Fair szabályt, akkor a következőpen értelmezte a szabályt:" … » szigorú«, mert dezertálással torolja meg, ha az előző menetben szívott (ő kooperált, a partnere dezertált). Viszont » igazságos«, mert nem torolja meg a partner dezertálását, ha vele együtt ő is dezertált korábban, és nem folytatja tovább a partnere kizsákmányolását akkor, ha az előző menetben egyszer már kihasználta őt." [Marcu]
Ez az indoklás ahhoz hasonlít, amit a Contrite TFT stratégia bemutatásakor már elmondtunk egyszer – bár az érvelésben tetten érhető egyfajta elmozdulás a büntetés irányába. Ego úgy értékeli Alter előző fordulóbeli dezertálását, hogy az igazolt büntetés volt Ego's saját korábbi dezertálásával szemben, és mivel Ego egyfelől egyetért az igazolt büntetés intézményével ('firm'), másfelől igazságos ('but fair'), így Ego kooperál Alter lépésére válaszul. Közös szlogenjük ez lehetne: 'ne büntesd, aki büntet'. A Pavlov vagy WSLS stratégia jellemzésekor többen kiemelték annak tanulási képességét, mi több, ezzel magyarázták a stratégia sikerességét is. Amikor ezt a cselekvési szabályt állítjuk párba a Stern Judging értékelési szabállyal, akkor – a büntetéshez való viszonyra fókuszálva – kicsit átértelmezhetjük a Pavlov szabály logikáját, hatásmechanizmusát. Rosas úgy értékeli, hogy a Pavlov/Stern Judging szabálykettős hízelgő (flattery), alázatos (obsequious) stratégia [Rosas] Szerintem inkább arról van szó, hogy a Pavlov esetében is a Stern Judging módszer logikája érvényesül. Mindkét szabály hasonlóképpen értelmezhető. Ego úgy értékelheti Alter's kooperálását Egoval szemben, hogy ezzel Alter tartózkodott megbüntetni Egot, aki pedig dezertált az előző fordulóban. A dezertálás büntetése viszont Alter kötelessége lett volna, s mivel ezt elmulasztotta, ezért Ego ezt a kooperálás helytelennek tartva böntetéssel (dezertálással) sújtotta. Ez volt a Stern Judging értékelési szabály logikája, és ez az indoklás érvényes, alkalmazható a Pavlov cselekvési szabály esetében is. Éppen ezért lehet mindkettejük receptje a következő szabály: 'büntesd, aki nem büntet'. Mind a haragtartó (Grim Trigger), mind a Shunning szabály erősen, vagy inkább túlzottan büntetéspártinak mondható. Nem véletlen, hogy a szimulációk során kiderült, hogy ezek a stratégiák nehezen, ritkán vezettek a kooperációs minták elterjedéséhez. A haragtartó stratégia az első dezertálásra végnélküli büntetéssel reagál, azaz bármit is tesz a partnere, a stratégia képviselője válogatás nélkül dezertál. A Shunning módszer is ugyanezt a logikát követi, csak ebben az esetben a partner "rosszasága" váltja ki ezt az egyértelmű elkülönülést. A közös vonásuk tehát az, hogy büntetik mind a kooperációt, mind a dezertálást, ami úgy is értelmezhető, hogy nem az – ilyen vagy olyan – cselekvést, hanem magát a cselekvőt utasítják el. Elvük lehetne: 'büntess mindent'. A négy stratégiakettős bemutatása alapján megállapíthatjuk, hogy négy párhoz négy alapelvet társíthatunk, amelyek mindegyike a büntetéshez való eltérő viszonyulást fejez ki. Ezt összegzem a következő táblában.| szabálypár | közös elv | |||||||||||||
| egyszerű TFT & Image Scoring | büntesd, aki büntet | |||||||||||||
| bűnbánó TFT & Simple Standing | ne büntesd, aki büntet | |||||||||||||
| Pavlov & Stern Judging | büntesd, aki nem büntet | |||||||||||||
| haragtartó & Shunning | büntess mindent | |||||||||||||
A játékok koalíciós kiterjesztése elköteleződésekkel
A kooperatív és nem-kooperatív játékok fogalmát John Nash vezette be. Kétféle módon szokták magyarázni, mit is jelent ez a megkülönböztetés. Egyfelől nem kommunikálhatnak egymással, ami azért fontos, mert nem így nem köthetenek egyezséget a partnereikkel a játékosok annak érdekében, hogy kikerüljenek a társadalmi csapda helyzetekből.| magjátékok | ||||||||||||||
| aszimmetrikus játékok | szimmetrikus | |||||||||||||
| többalternatívás játékok | kétalternatívás | |||||||||||||
| többszereplős játékok | kétszereplős | |||||||||||||
| nem szigorúan rendezett játékok | szigorúan rendezett | |||||||||||||
| aszinkron játékok | szinkron | |||||||||||||
| ismételt játékok | egyszeri | |||||||||||||
| direkt reciprocitás játékok | ismerős játékosok | |||||||||||||
| indirekt reciprocitás játékok | ismeretlen játékosok | |||||||||||||
| kooperatív (ígéret) játékok | kooperatív (ígéretmentes) | |||||||||||||
Pozíció, szerep, norma, uralom
"A jogtudományt tanuló angol diákok döntő többsége a jog alapvető kategóriáival való ismerkedést Hohfeld 'Alapvető jogi fogalmak' című tanulmányával kezdi."
[H.L.A]
"Egy rossz normától megszabadulni mindannyiunk érdeke, mégis sokszor nagyon nehéz elérni ezt."
[Crist]
[Crist]
"A karizma az a képesség, hogy hatni tudjunk másokra logika nélkül." (Quentin Crisp)
Perszonális deontika
A logikai alapozó fejezetben jeleztem (☜) hogy a deontikus logika évtizedeken keresztül személytelen, imperszonális módon építkezett. Megkockáztatom, hogy az imperszonális megközelítés dominanciája is hozzájárult ahhoz, hogy a deontikus logika hosszú időn át nem tudta beváltani a hozzá fűzött kezdeti reményeket. Sokan várták ugyanis, hogy a deontikus logika fejlődése során hamar eléri az a szintet, amikor már megfelelő alapokat képes nyújtani jogi, normatív szövegek formális leírásához, a jogi szövegek konzisztenciájának vizsgálatához és ezáltal jogi szövegek számítógépes feltárásához. Ez azonban nem következett be. Nem is nagyon következhetett be, mert amíg a deontikában nem lehetett személyközi viszonyokat kifejezni, kezelni, addig nem lehetett megragadni a jogban, normativitásban alapvető jogi, normatív viszonyokat. A társadalmi kapcsolatok feltárásához szükség volt arra, hogy az ágensek közti kapcsolatokat is kezelni lehessen a deontikán belül. A deontikus logika a deontikus modalitások, a kötelezések, tiltások, megengedések, eltekintések logikájával foglalkozik. Amíg imperszonális deontikát "űzünk", azaz amíg egyetlen ágenst feltételezünk, amíg egyetlen deontikus operátoron van a fókuszunk, amivel ki tudunk fejezni egy normatív, deontikus állítást, addig nem tudjuk megragadni a jognak (normativitásnak) azt a minőségét, alapvonását, hogy a létező jogi (normatív) rendszerekben jogi (normatív) viszonyokat kell kezelnünk. Ez a deontika nyelvén azt jelenti, hogy a deontikus operátorokkal kifejezhető normatív aktusokat mindig "párosával", egymással összekapcsolódva kell értelmeznünk. A jogtudománynak már nagyon régóta az egyik alapvetése ez a tétel [StigK] Ahol valakinek jogosultsága van valamire, ott van valaki más, aki valamilyen kötelezettséggel rendelkezik az adott jogosultsághoz kapcsolódóan. Vagy fordítva: a kötelezettségek mindig mások jogosultságával járnak együtt. W.N. Hohfeld egyetértőleg idézi az alábbiakat:"Kötelesség vagy jogi kötelezettség az, amit valakinek meg kell tennie vagy nem szabad megtennie. A 'kötelesség' és a 'jog' korrelatív kifejezések. Ha megsértenek egy jogot, megszegnek egy kötelességet is." [hohfe]
A jogbölcseletben vita van arról, vajon csak általában vagy mindig érvényes ez a fajta komplementaritás. Vannak nagy hatású jogelméleti gondolkodók, akik vitatják a korrelativitás teljeskörűségének tézisét. Joseph Raz például így ír:"Egy népszerű nézet szerint minden joghoz tartozik egy korrelatív kötelezettség. Minthogy a jog a kötelezettség egyik alapja, jó adag igazság van az efféle korrelativitás-tézisben. A tézis legtöbb szokásos megfogalmazása mégis félrevezető." [JRaz:]
Ebben a vitában nem tudok, nem is akarok állást foglalni, és mivel a fomális modell építésének jelen szakaszában nem is igazán lényeges ez a kérdés, el lehet tekinteni e szempont figyelembe vételétől. Lehet, hogy igaza van Joseph Raznak, és nem áll mindig a korrelativitás tézise, de azt Raz sem tagadja, hogy sok esetben igaz. Ha viszont azt állíthatjuk, hogy a jognak, normativitásnak vannak olyan területei, ahol diadikus viszonyokat, azaz jogi relációkat kell kezelnünk, akkor a jogi fogalmak fent hivatkozott kettősségét, korrelativitását valahogy be kell építeni a fogalmi modellünkbe. Ezt a relációs jelleget úgy tudjuk megragadni, ha a imperszonális szemléletmódot felváltjuk a perszonális megközelítéssel. A továbblépés előtt azonban szükséges figyelmeztetnem arra, hogy az elemzendő fogalmak, terminusok mindennapi használatában sajnos sokfajta és elég széles körben elterjedt pongyolaság figyelhető meg. A terminusokat sokszorosan túlhasználják, vagyis egy-egy terminust – sokszor akaratlanul – többféle jelentéssel vesznek használatba, és ez sok esetben nagyon könnyen fogalmi zavarokhoz, félreértésekhez vezethet. Érdemes ezért itt egy-két előzetes megjegyzést tennem. A jog a deontikus logika operátorait kifejező terminusok közül a kötelezést és a tiltást kiterjedt módon alkalmazza, ám a megengedés terminusát ritkábban veszi igénybe (ha egyáltalán használja). Sokkal elterjedtebb a jog, jogosultság terminusa. Ennek ellenére nyugodtan rögzíthetjük, hogy a jog, jogosultság, megengedés terminusai mind ugyanahhoz a jelentéstartományhoz sorolhatók, mint ahová a megengedés is tartozik. Ebből persze az is következik, hogy akárcsak a megengedés kategóriája esetében, úgy a jogosultság mindennapi használatában is keveredik az a két lehetőség, hogy a nem-kötelezés vagy a nem-tiltás állapotát fejezzük-e ki a terminussal. Mivel a hétköznapi fogalomhasználati gyakorlatba mindkét értelmezés mélyen beleivódott, értelmetlen lenne bármelyik interpretációt elsődlegessé tenni a másik ellenében, így csak arra törekedhetünk, hogy tudatosan figyelve erre a problémára, a terminusok használata során mindig egyértelművé tegyük, az adott pillanatban éppen melyik értelmezés tartjuk érvényesnek. A szinonimitásról beszélve megállapíthatjuk még, hogy a kötelezettség és kötelesség terminusait is egymással felcserélve lehet használni. Sajnos létezik egy másik terminológiai pongyolaság jogi alapfogalmak területén, ami a laikusok számára még több problémát, félreértést okozhat – legalábbis a magyar nyelvben. A 'jog' terminusa ugyanis többféle értelemben használható. A jog egyfelől jelenthet jogosultságot, illetve másfelől normatív megnyilatkozást, és az utóbbi jelenthet egyetlen normatív kijelentést (mint jogszabály, jogtétel), de jelentheti akár az egész jogi rendszert is. Az igazi megkülönböztetést a jog mint jogosultság és a jog mint normatív rendszer (tételes jog) között kell megtennünk, a jogtétel és a tételes jog közti különbség inkább mennyiségi, nem annyira minőségi. Természetesen a jogtudomány réges rég elvégezte ezt a megkülönböztetést, hiszen az 'alanyi jog' (facultas agendi) és a 'tárgyi jog' (norma agendi) fogalmai lényegileg erre a kettősségre reflektálnak. Ami nagyon fontos (és ez sokak számára szokatlan, meghökkentő lehet), fogalmilag szükségünk van a 'jogi jog' és 'erkölcsi jog' elhatárolására egymástól, amit csak a jog fogalmának pontos explikációja, sokszálú értelmezése révén tehetünk meg. Amikor a későbbiekben a norma fogalmát fogom tipizálni a különböző fogalmi összetevők alapján (☜) akkor a különböző tipizálási lehetőségek egymás utáni kibontásával jobban lehet majd érzékeltetni, hogy valóban értelmes kategória akár a 'jogi jog', akár az 'erkölcsi jog' fogalma. Másfajta fogalmi zavar jelentkezik a jogi viszonyok minősítésében. Itt nem terminológiai (poliszémikus jellegű) túlhasználásról, hanem fel nem ismert szinonimitásról van szó. Amikor a jogtudósok az összetartozó jogokról és kötelességekről beszélnek, akkor a köztük levő viszonyra a 'korrelativitás' terminusát alkalmazzák. Wesley Newcomb Hoh-feld is a korrelativitás kategóriáját használta. A mai napig bevett ez a szóhasználat a jog világában. Később, amikor elemezni fogom a szociológusok által bevezetett társadalmi szerep fogalmát (☜) szólok arról, hogy a társadalmi szerepek normatív összetevői közt ugyanúgy jogokat és kötelességeket találhatunk, mint a jog esetében. A szociológusok azonban az általuk vizsgált normatív komponensek közt megfigyelhető viszonyt más kategóriával ragadják meg, ők erre a komplementaritás terminusát használják. Hohfeld fogalmait elemezve a korrelativitás terminusa helyett Stig Kanger két másik kategóriát javasol alkalmazni [StigK] Később bemutatom, hogy Kanger milyen alapon minősíti hol inverz, hol konverz relációnak két jogviszony közt létező korrelativitást. Jogi szövegekben előfordul olykor a jogi viszonyok 'reciprocitása' kifejezés is, ami szintén a korrelativitás, komplementaritás jelenségéhez kapcsolódik. Nagyon hasonló tartalom mentén van tehát négy-öt terminus, a korrelativitás, a komplementaritás, az inverzitás és konverzitás, illetve a reciprocitás, amelyek közül nekem is választanom kell majd. Mivel az empirikus társadalomtudományokban a korreláció fogalmának a korrelativitás itteni tartalmához képest nagyon más jelentése van, ezért a korrelativitás helyett inkább a komplementaritás kategóriáját fogom használni, illetve ahol szükség lesz a nagyobb pontosságra, ott a konverzitás és inverzitás terminusait is alkalmazni fogom. És mindezek mellett – ha történeti vagy olykor stilisztikai okokból szükségesnek látszik – megengedhetőnek tartom a korrelativitás terminus használatát is. Mivel a reciprocitás fogalma nagyon erősen használt a társadalomtudományokban, nem tartanám szerencsésnek ezt a fogalmat az itt tárgyalt jelentésben is használatba venni.Normatív pozíciók
A társadalmi cselekvések indoklásai során rengetegszer hivatkozunk a jogainkra, a jogosultság fogalmára. Ilyeneket mondunk: Ezek a példák azt jelzik, hogy egyrészt a jogaink irányulhatnak tevőleges cselekvésre (csinálásra), illetve nem-cselekvésre (tartózkodásra), másrészt a jogaink vonatkozhatnak a saját, illetve mások cselekvésére, harmadrészt a jogaink tetszőleges cselekvésre irányulhatnak, de olykor "csak" azt szabályozzák, hogy a jogi-normatív viszonyainkat megváltoztathatjuk-e vagy sem. De a fenti példák azt is mutatják egyben, hogy a jogosultságainkhoz valóban hozzárendelhetők mások kötelezettségei. Amikor például a kölcsönadott pénzt várjuk vissza, akkor mindig valaki más kötelezettségére gondolunk (akinek vissza kell adnia a pénzt), vagy ha nekem jogom van erőszakmentes életre, akkor azt is jelenti egyben, hogy mindenki másnak tilos megvernie engem (kötelező tartózkodnia az erőszak alkalmazásától). Végül a példákból kitetszik az is, milyen sokféle jelentést sűrítünk a jog-jogosultság fogalmába. Itt az idő, hogy megnézzük, hogyan lehet szétszálazni ezt az összefonódó sokféleséget.Hohfeld elsőrendű jogviszonyfogalmai
Wesley Newcomb Hohfeld volt az, aki miután észlelte, hogy a jog(osultság) és kötelesség fogalmát sokszorosan túlhasználják a jogászok, megpróbálta elválasztani a különböző jelentésrétegeket egymástól. Hohfeld két tanulmánya a jog és kötelesség fogalmainak többértelműségéről csak a halála után, 1913-ban és 1917-ben jelent meg. [♦] A jogosultságok és kötelezettségek közti korrelatív kapcsolat tézise már Hohfeld előtt is nyilvánvaló volt a jogtudományon belül [StigK] Hohfeld azzal hozott újdonságot, hogy rámutatott, a jogosultság, illetve kötelezettség fogalmaiban meghúzódó jelentésrétegek hogyan különíthetőek el egymástól.Hohfeld jogfogalmainak struktúrája
Hohfeld szerint négy-négy jogosultság-, illetve kötelezettségtípust definiálhatunk, és ezek mindegyikét kétféle módon is kapcsolatba hozhatjuk egymással. Minden jogosultságnak van egy ellentéte, illetve van egy korrelatív párja a kötelezettségek között (és természetesen mindez igaz fordítva is, a kötelezettségekhez is rendelhető jogosultság). Hohfeld a következő kategóriákat vezette be.| right | privilege | power | immunity | |||||||||||
| duty | no-right | liability | disability | |||||||||||
| jog | szabadság | felhatalmazottság | mentesség | |||||||||||
| kötelezettség | joghiány | beavatkozásnak kitettség | beavatkozásképtelenség | |||||||||||
| legal relation | jogi viszony | korrelatív párja | ellentéte | |||||||||||
| right | igényjog | kötelezettség | igényhiány | |||||||||||
| duty | kötelezettség | igényjog | szabadság | |||||||||||
| privilege | szabadság | igényhiány | kötelezettség | |||||||||||
| no-right | igényhiány | szabadság | igényjog | |||||||||||
| power | felhatalmazottság | beavatkozásnak kitettség | beavatkozásképtelenség | |||||||||||
| liability | beavatkozásnak kitettség | felhatalmazottság | mentesség | |||||||||||
| immunity | mentesség | beavatkozásképtelenség | beavatkozásnak kitettség | |||||||||||
| disability | beavatkozásképtelenség | mentesség | felhatalmazottság | |||||||||||
Az ábra nemcsak azt mutatja, hogy mely fogalmak között van ellentétes, illetve korrelatív viszony, de az is "leolvasható" róla, hogy a fogalmak két csoportra oszthatók. Az egyik csoport az igényjog, a másik felhatalmazottság köré szerveződik, és mindkettő csoportnak hasonló belső mikrostruktúrája van. A későbbiekben majd kiderül, hogy milyen kapcsolat van a két csoport, illetve a két csoport elemei között.
Az igényjog köré szerveződő fogalmak értelmezése
A hohfeldi jogfogalmak struktúráját már bemutattam, de se nem definiáltam, se nem adtam példákat az egyes fogalmakra, pedig az értelmezésükhöz, modellbe építésükhöz mindkettőre szükség lenne. Első körben bemutatom Hohfeld saját meghatározásait, miközben igyekszem tőle (vagy a korai Hohfeld-recepcióból) származó példákat hozni rájuk. Az első fogalmi csoport középpontjában a jogigény kategóriája áll, aminek komplementere a kötelezettség és ellentéte a joghiány fogalma. Hohfeld példája így szól." … ha X-nek joga van ahhoz, hogy Y az ő földjén kívül tartózkodjék, ezzel korrelatív (és ennek megfelel) Y azon kötelessége, hogy maradjon távol attól a helytől." [hohfe]
A fenti idézetben Hohfeld két jogi terminust nevez meg (az igényjogot és a kötelezettséget), de ezzel igazából nem két "különálló" jogviszonyt állít szembe egymással. Az igény és a kötelezettség voltaképpen ugyanannak a jogviszonynak két "nézetét" jelenti. [♦] Ezért mondja rájuk Hohfeld, hogy korrelatív kapcsolatban vannak egymással. A két jogviszonyt így bonthatjuk fel összetevőkre.| jogosult & jogviszony &cselekvő& \multicolumn{2}{l}{cselekvés}\\ | ||||||||||||||
| Ego | igénye | Alter | nem | átjárni Ego telkén | ||||||||||
| Alter | kötezettsége | Alter | nem | átjárni Ego telkén | ||||||||||
" … ha X-nek joga vagy igénye van arra, hogy Y – valaki más – maradjon távol földjétől, akkor neki magának megvan az a szabadsága, hogy belépjen e területre; másként fogalmazva, X-t nem terheli a távolmaradás kötelezettsége. A belépés szabadsága a kívülmaradás kötelezettségének ellentéte." [hohfe]
Szabadság és kötelezettség tehát ellentétes fogalmak, de pontosan látni kell, mit is ért Hohfeld az 'ellentétes' fogalom jelentése alatt." … e ponton nem árt némi óvatosság; hiszen amikor azt mondjuk: egy adott szabadság egy kötelezettség puszta negációja, akkor ezt természetesen mindig úgy értjük, hogy a kötelezettség tartalma az, ami pontosan ellentétes a kérdéses a kérdéses szabadságéval." [hohfe]
A telektulajdonosnak szabadsága van saját telkén átjárnia, másoknak kötelezettségük van tartózkodni az átjárástól. Utóbbi úgy is értelmezhető, hogy mások kötelesek nem átjárni a tulajdonos telkén. Ha Egora és Alterre vonatkoztatjuk mindezt, akkor a következő formában adhatjuk meg a két jogviszony összetevőit.| jogosult & jogviszony & cselekvő& \multicolumn{2}{l}{cselekvés}\\ | ||||||||||||||
| Ego | szabadsága | Ego | átjárni Ego telkén | |||||||||||
| Alter | kötelezettsége | Alter | nem | átjárni Ego telkén | ||||||||||
"Amit a jog [az igényjog] hozzátesz a szabadsághoz, az másoknak az a kötelessége, hogy tartózkodjanak a beavatkozástól." [JoelF]
Feinberg arra utal, hogy Hohfeld két kategóriáját szigorúan el kell választani egymástól, a szabadság nem feltételezi – sem logikailag, sem gyakorlatilag – a jogigény létezését. A szabadság önmagában még nem teremti meg, nem hozza magával azt az igényjogot, hogy az Alter nem avatkozik be, nem zavarja meg Egot abban a cselekvésben, amire Egonak szabadsága van. Hohfeld példája arra, hogy a szabadság nem keletkeztet korrelatív kötelezettséget a másik fél be nem avatkozásra, így szól."A, B, C és D mint salátatulajdonos esetleg azt mondja X-nek: 'Edd meg a salátát, ha tudod; engedélyezzük ezt neked, de nem értünk egyet azzal, hogy ne zavarjunk meg ebben.' Ebben az esetben a szabadság létezik, s amennyiben X-nek sikerül megennie a salátát, akkor nem sérti meg egyik fél jogát sem. Világos azonban az is, hogy ha A-nak sikerülne olyan gyorsan elkapnia a tálat, hogy X egy falatot sem tudna abból enni, úgy Y-nek semmilyen joga sem szenvedne csorbát." [hohfe]
A példa szemléletesen rávilágít, hogy mi a különbség a kétfajta jogviszony, az igény és a szabadság között. De vehetek egy másik példát a hétköznapok világából. Ha egy vonatra helyjegyet veszek, akkor igényjogom keletkezik arra, hogy leüljek a székemre. Ha valaki ül azon a széken, amire a helyjegyem szól, akkor igényelhetem tőle, hogy adja át a helyét, és ezzel "párhuzamosan" neki kötelessége lesz felállni. Ha viszont nem helyjegyes vonaton utazom, akkor szabadságom van a még szabad székek bármelyikére leülnöm, de nem igényelhetem senkitől sem, hogy adja át nekem azt a széket, amin ő ül. Viszont ha én leülök egy szabad székre, utána nem leszek köteles átadni az a helyt valaki másnak, ezt senki sem igényelheti tőlem. Amíg viszont vannak szabad székek, addig bárki elfoglalhatja azok bármelyikét, és megakadályozhat engem abban, hogy a kiszemelt szabad helyre leülhessek, ha ő előbb teszi ezt meg. Nem könnyű észrevenni a szabadság "függetlenségét" az igényjogtól, már ha valóban magában áll. A tényleges gyakorlatban a jogviszonyok az esetek nagy részében összetettek, és a szabadság és igényjog együttjár. Így van ez például a tulajdonjog esetében. De ez a gyakorlati együttjárás semmiképpen sem jelent logikailag szükségszerű összetartozást köztük. Ha viszont a szabadság hol magában, hol az igényjoggal együtt fordul elő a különböző gyakorlati jogfogalmak között, akkor ezt a kétféle helyzetet, pontosabban e kétféle helyzetre jellemző szabadságfogalmat érdemes lehet jelzős szerkezetbe téve elkülöníteni egymástól. Erre tett javaslatot Jeremy Bentham, aki a nyers szabadság (naked liberty), illetve a szerzett szabadság (vested liberty) fogalompárt javasolta alkalmazni erre a kétféle helyzetre (Bentham nézeteit ismerteti: [LarsL] Amikor a szabadság csak magában áll, akkor nyers, védtelen ahhoz képest, amikor az igényjoggal kiegészülve védve van a mások általi beavatkozástól. A nyers szabadságban megtehetünk mindent tetszésünk szerint, de mindenki másnak szabadsága van megakadályozni minket saját szabadságunk (akaratunk) érvényesítésében. A védett szabadságban a beavatkozás tiltva van a többiek részére. Nem ejtettem még szót az utolsó hohfeldi kategóriáról, a joghiányról. Ez a fogalom az igényjog ellentéte és a szabadság korrelatív párja. A korrelativitás azt jelenti itt, hogy az egyik fél (Ego) szabadsága megtenni valamit megegyezik azzal, hogy a másik félnek (Alternek) joghiánya van (nincs igénye) arra, hogy az egyik (Ego) ne tegye meg azt." … X azon jogának korrelatív párja, hogy Y ne lépjen a földjére, azonos Y azon kötelezettségével, hogy ne tegye azt; X azon szabadságának korrelatív párja azonban, hogy saját földjére lépjen, azonos Y azon 'jogának hiányával', hogy igényelhesse X távolmaradását." [hohfe]
Az ingatlanos példa jogviszonyait kifejező mondatok összetevőkre bontásával a következő táblázatot kaphatjuk.| jogosult & jogviszony &cselekvő& \multicolumn{2}{l}{cselekvés}\\ | ||||||||||||||
| Ego | szabadsága | Ego | átjárni Ego telkén | |||||||||||
| Alter | igényhiánya | Ego | nem | átjárni Ego telkén | ||||||||||
| jogosult & jogviszony &cselekvő& \multicolumn{2}{l}{cselekvés}\\ | ||||||||||||||
| Ego | igénye | Alter | nem | átjárni Ego telkén | ||||||||||
| Alter | igényhiánya | Ego | nem | átjárni Ego telkén | ||||||||||
| jogosult & jogviszony &cselekvő& \multicolumn{2}{l}{cselekvés}\\ | ||||||||||||||
| Ego | igénye | Alter | nem | átjárni Ego telkén | ||||||||||
| Alter | kötelezettsége | Alter | nem | átjárni Ego telkén | ||||||||||
| Ego | szabadsága | Ego | átjárni Ego telkén | |||||||||||
| Alter | igényhiánya | Ego | nem | átjárni Ego telkén | ||||||||||
| jogosult & jogviszony &cselekvő& \multicolumn{2}{l}{cselekvés}\\ | ||||||||||||||
| Ego | szabadsága | Ego | nem | átjárni Ego telkén | ||||||||||
| Alter | igényhiánya | Ego | átjárni Ego telkén | |||||||||||
Az igényjog köré csoportosítható jogviszonyok felbontása
A hohfeldi jogviszonyfogalmak pontosítása, egyértelmű formalizálása érdekében első lépésként érdemes grafikai eszközökkel reprezentálni a kategóriák közti viszonyokat. Egy hohfeldi jogviszonyt négy változóval írhatunk le. Mindig meg kell adnunk a jog típusát, a jog birtokosát, a jog tartalmát adó cselekvés típusát és e cselekvés ágensét. Ezt az alábbi formulában összegezhetjük.| (i) – $right(Agent, \pm do(Agent,T(\pm p,\pm p)))$ |
| (ii) – $right(Agent, \pm do(Agent))$ |
| acea |
| a jog (right) típusa: | claim $\mid$ liberty $\mid$ duty $\mid$ no-claim |
| a jog birtokosa (Agent): | Ego (E) $\mid$ Alter (A) |
| a jog tartalmát adó cselekvés ($\pm$do): | do $\mid \lnot$do |
| a cselekvés ágense (Agent): | Ego (E) $\mid$ Alter (A) |
A nyolc síkot négy-négy térnegyedbe rendezhetjük azon az alapon, hogy milyen cselekvésről van szó (vagyis kinek a milyen cselekvéséről beszélünk). Az a) jelű térnegyedben Alter tevésével, a b) jelűben Alter tartózkodásával, a c) jelűben Ego tevésével, a d) jelűben Ego tartózkodásával kapcsolatos jogviszonyok láthatóak úgy, hogy egy-egy negyedbeli síkon Ego, illetve Alter jogai vannak "összekötve". Észre kell vennünk azonban, hogy nem minden – logikailag lehetséges – jogviszony értelmes. Az igény (jogigény) például csak akkor értelmezhetó, ha a jogbirtokos és a cselekvő különbözik. Nincs értelme saját cselekvésemre irányuló igényről beszélni. Ezen a ponton ugyanis feltételezhetjük, hogy egy ágens saját cselekvésére irányuló akarata egyértelmű, ha valaki akar valamit, akkor azt végre is hajtja. [♦] Ugyancsak (és ugyanazért) értelmetlen az igényhiány fogalma is azonos ágensek esetében. Tartalmatlannak tarthatjuk a szabadság fogalmát is – eltérő ágensekre vonatkozóan. A szabadság csak saját cselekvésemet illetően értelmes, mással cselekvésére vonatkozóan nekem nincs, nem lehet szabadságom. Ugyanez igaz a kötelezettségre is: csak magamat illetően lehetnek kötelezettségeim, másokra nézve csak a kötelezettségre vonatkozó igényem képzelhető el.
Ha mindezek alapján a "nem értelmes" fogalmakat töröljük a "palettáról", akkor már csak 16 jogviszonyhoz jutunk. Ha ezek között feltüntetem a hohfeldi korrelativitási kapcsolatokat, akkor a következő ábrát kapjuk:
Az ábrán már nem láthatóak az "értelmetlen" jogviszonyok, csak azok szerepelnek, amelyek a hohfeldi értelmezésekben felbukkantak, felbukkanhattak. A korrelativitást jelző vonalak "átkötései" más negyedekbe szépen mutatják azt, hogy a jogfogalmak közti belső összefüggések másfajta cselekvéseket kapcsolnak össze. Az ábra tehát azt is szemlélteti egyben, hogy a fogalmak pontos értelmezéséhez mennyire fontos figyelembe venni azt, hogy milyen cselekvésre vonatkoznak a jogviszonyok. Hohfeld sajnos nem igazán reflektált erre a kérdésre. A jogviszonyok elméletileg teljesnek mondható ábráját tovább egyszerűsíthetjük úgy, hogy két-két negyedet "összecsúsztatunk". Ha az egymás alatt levő negyedekkel (tehát az a) és c), illetve a b) és d) jelűekkel) tesszük meg ezt, akkor olyan síkokhoz jutunk, amelyek ugyanannak a jogbirtokosnak a jogviszonyait mutatják. A két alsó síkon Ego, a két felső síkon Alter jogviszonyai láthatók. A jobb áttekinthetőség kedvéért a jobb oldali két síkot tükröztem a függőleges tengely mentén, mert így jobban láthatókká váltak a korrelativitási kapcsolatok. Ez alapján már könnyben értelmezhető ábrát kapunk, hiszen már csak feleannyi pozíciót kell értelmeznünk.
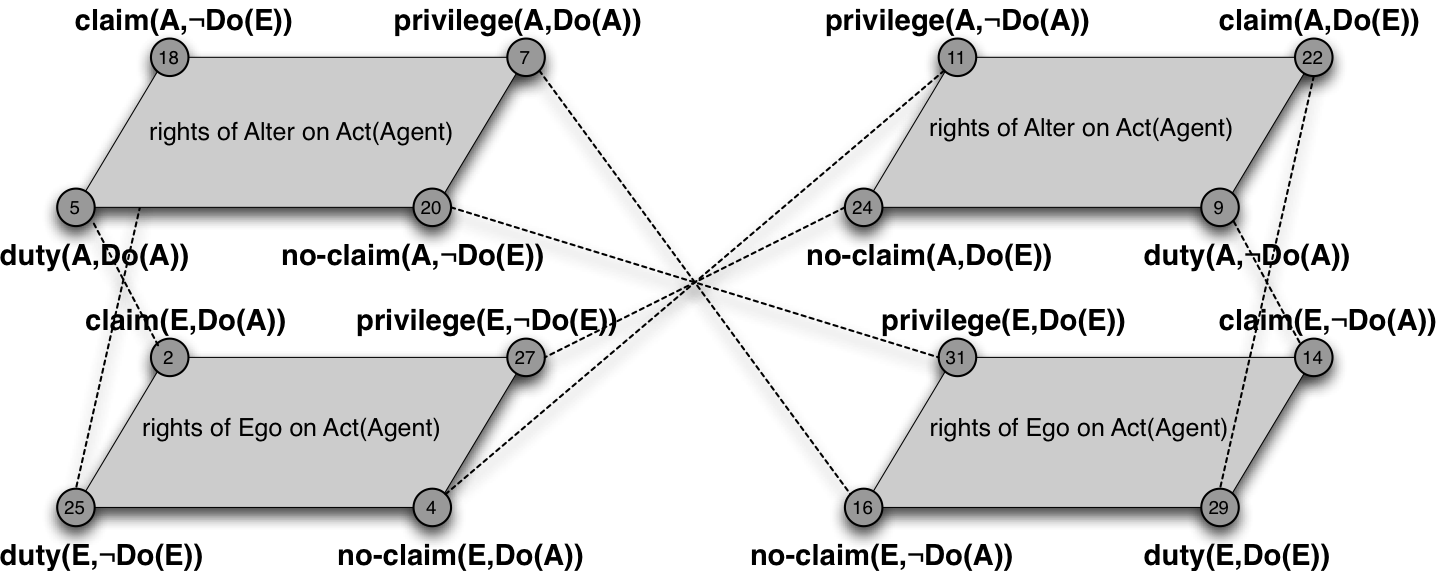
Egy utolsó átrendezést végrehajtva a Hohfeldi sémához nagyon hasonló szerkezethez juthatunk. Csak annyit kell tennünk, hogy a két felső síkot a vízszintes tengelyük körül elforgatjuk 180 fokkal (vagyis a síkok felső és alsó csúcspontjait megcseréljük egymással), majd ezután a két felső sík privilege és no-claim jogviszonyait kicseréljük egymással, végül a második kocka csúcspontjait a lapra merőleges, függőleges síkra vetítve tükrözzük. Ekkor ugyanúgy az alsó két síkon helyezkednek az Ego, a felső két síkon az Alter jogviszonyai, viszont a korrelatív kapcsolatok egymás fölé kerülnek, és az egész struktúra két részre "esik szét". A két kocka elemei csak abban térnek el egymástól, hogy mindig az ellentétes cselekvésre vonatkozó jogviszonyt írják le.
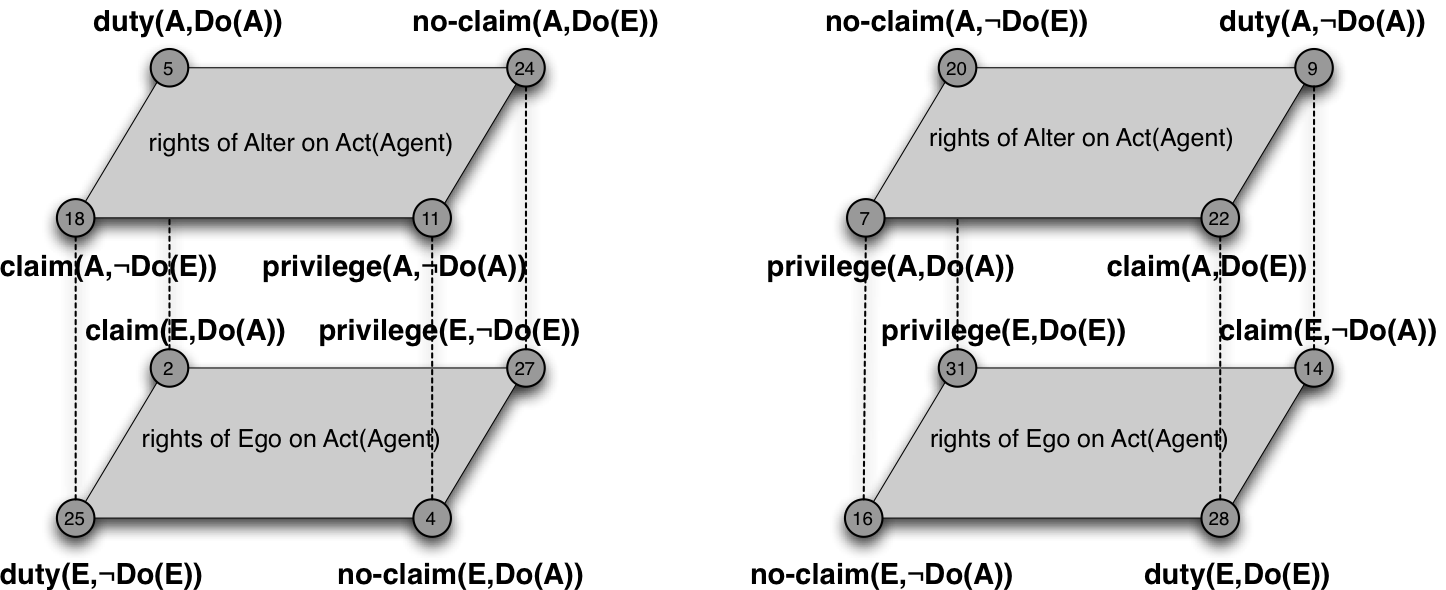
Mindkét ágens jogviszonyai között (tehát a felső és alsó két síkon) találhatunk két-két négyes csoportot. Mindkét ágens esetében négy-négy jogfogalom összetartozik azon az alapon, hogy a jogviszony az ágens saját vagy a partnere cselekvésére irányul-e (mindig a Duty és Privilege, valamint a Claim és No-claim fogalmak kapcsolódnak így össze). Ezeket a fogalmi négyeseket lehet majd deontikus logikai formulák segítségével megragadni. Az ábrából az is kiderül, hogy Hohfeld négy-négy jogosultság, illetve kötelezettség fogalma kevés, valójában kétszer annyira van szükség. Az utolsó ábra "eredményeit" táblázatos formában, szövegesen is reprezentálhatom. A pozitív és negatív cselekvést tevésnek és tartózkodásnak írva a már megszokott táblázatos formában az alábbi módon írhatjuk fel a nyolcféle jogviszonyt.
| jogosult | jogviszony | ágens | cselekvés | jogosult | jogviszony | ágens | cselekvés | |||||||
| Ego | igénye | Alter | tartózkodni | Alter | kötelezettsége | Alter | tartózkodni | |||||||
| Ego | szabadsága | Ego | megtenni | Alter | igényhiánya | Ego | tartózkodni | |||||||
| Ego | igénye | Alter | megtenni | Alter | kötelezettsége | Alter | megtenni | |||||||
| Ego | szabadsága | Ego | tartózkodni | Alter | igényhiánya | Ego | megtenni | |||||||
| Ego | kötelezettsége | Ego | tartózkodni | Alter | igénye | Ego | tartózkodni | |||||||
| Ego | igényhiánya | Alter | megtenni | Alter | szabadsága | Alter | tartózkodni | |||||||
| Ego | kötelezettsége | Ego | megtenni | Alter | igénye | Ego | megtenni | |||||||
| Ego | igényhiánya | Alter | tartózkodni | Alter | szabadsága | Alter | megtenni | |||||||
"Mivel mind a negatív, mind a pozitív jogok passzívak, vannak olyan jogok, amelyek se nem negatívak, se nem pozitívak. A szabadság és a felhatalmazottság nem lehet negatív jog, a szabadság, felhatalmazottság és a mentesség nem lehet pozitív jog. Az a jog (szabadság), hogy belépsz egy épületbe, vagy az a jog (felhatalmazottság), hogy magadra vállalod egy szerződés kötelmeit, se nem negatív, se nem pozitív." [LeifW]
Nem értek teljesen egyet ezzel a gondolatmenettel. Azon a ponton mindenképpen tévesnek tartom, amikor a pozitív/negatív jog kettősségét a passzív jog fogalma alá rendeli. A pozitív és negatív jog megkülönböztetése ugyanúgy értelmes az aktív jog esetében is. Ezt mutatom meg a továbbiakban. Adja magát, hogy azonnal hivatkozzak itt a kérdés leghíresebb szerzőjére, Isaiah Berlinre, aki a 'A szabadság két fogalma' című tanulmányában definiálta a pozitív és negatív szabadság fogalmát [Isaia] és ezzel megalapozta, hogy e két fogalom hosszú időre bekerüljön a jogok típusairól szóló diskurzusba. Arra azonban nagyon vigyázni kell Berlin kétféle szabadságfogalma kapcsán, hogy ne tévesszen meg minket a terminusszintű azonosság. Berlin ugyanis – részben vagy teljesen – más értelemben használja a fogalmait. Talán úgy tudom legpontosabban megmutatni, hogy miben és hol tér el egymástól a hohfeldi és berlini értelmezés, ha előbb megvizsgálom Jan Narveson szabadságfelfogását. Narveson is kétféle szabadságfogalmat definiál, hasonló szellemben, mint ahogy azt Berlin is teszi, csak még általánosabb formában [JanNa] Pozitív szabadság (positive freedom) fogalma alatt Narveson azt az állapotot érti, amikor minden szükséges feltétel adott ahhoz, hogy valamely cselekvés végrehajtható legyen. Ezek a feltételek lehetnek külső és belső feltételek egyaránt. Utóbbira a foci szabályainak ismeretét, megfelelő testi kondíciót, előbbire a szükséges számú társ jelenlétét, focilabda, szabad focipálya meglétét hozza fel Narveson példaként. Ezzel szemben a negatív szabadság (negative freedom) fogalmát Narveson olyan állapotként definiálja, amelyből hiányzik minden olyan mozzanat, amely megakadályozná valamely cselekvés végrehajtását. Példa lehet erre egy másik, ugyanazon a pályán focizni vágyó társaság hiánya. Narveson tehát a kétféle szabadságfogalom értelmezésekor bármilyen feltételt "megengedhetőnek", figyelembe vehetőnek tart. Berlin a negatív szabadság fogalmával kezdi az elemzését, és abban az értelemben Narveson definíciójához hasonlítható Berlin meghatározása is, hogy a cselekvést akadályozó feltételek hiányaként értelmezi a negatív szabadságot.
"Kényszeríteni valakit annyi, mint megfosztani őt a szabadságától."
[Isaia]
"Általában azt mondják, hogy annyira vagyok szabad, amennyire más emberek vagy más emberekből álló csoportok nem avatkoznak be cselekedeteimbe. A politikai szabadság ebben az értelemben egyszerűen az a terület, amelyen belül az ember anélkül cselekedhet, hogy mások megakadályoznák ebben."
[Isaia]
"… a szabadság ebben az értelemben a valamitől való szabadságot jelenti, vagyis a változó, de mindig felismerhető határok áthágásának hiányát."
[Isaia]
"Mit ér a szabadság annak, aki nem tud mit kezdeni vele? Mi a szabadság értéke, ha nincsenek meg a felhasználásához szükséges feltételek?"
[Isaia]
"Egy cél elérésére való képtelenség önmagában nem jelenti a politikai szabadság hiányát. … Azt mondják, nagyon meggyőzően, hogy ha egy ember túl szegény ahhoz, hogy elérjen valamit, amit jogilag nem tilos – egy vekni kenyeret, egy világ körüli utat, vagy azt, hogy a bírósághoz fordulhasson jogorvoslatért –, éppoly kevéssé szabad, mint hogyha ezen dolgok elérésétől a törvény tiltaná el."
[Isaia]
"A » szabadság« szó » pozitív« értelme az egyénnek abból a vágyából fakad, hogy saját magának az ura legyen. Azt szeretném, ha életem és döntéseim rajtam múlnának, nem pedig holmi külső erők határoznának rólam. Saját akarati aktusomnak kívánok eszköze lenni, nem pedig másokénak. Szubjektum, nem pedig objektum akarok lenni, szubjektum, amelyet saját gondolatai, saját tudatos céljai irányítanak, s nem külső okok mozgatnak."
[Isaia]
A pozitív jogok " … nem érvényesíthetők bírósági úton: különleges szerepet töltenek be, és elsősorban arra szolgálnak, hogy az állami tisztségviselők és az állampolgárok összességének általános céljait megfogalmazzák.
A negatív jogok … azonban bírósági védelmet élveznek, és nem szükséges a bírói út igénybevétele előtt semmilyen más állami hatósághoz fordulni. Senki sem függhet az állami hatóságoktól, ha a jogait bíróság előtt kívánja étvényesíteni.
A gazdasági szabadságok megőrzésére tett erőfeszítéseket kísérheti az a tudatos törekvés, hogy csökkentsük a gazdasági jogok szerepét."
[CassR]
A jogelméleti diskurzus kétféle jogtipológiája, a pozitív-negatív jog, illetve az aktív-passzív jog fogalomkettőse csak kisebb részben, de azért használható a hohfeldi elmélet pontosítására. A passzív-aktív dimenzió a későbbiekben segíthet még minket a hohfeldi jogviszonyok értelmezésében, de a modellépítésnek jelen fázisában nem alkalmazható. A pozitív-negatív jog megkülönböztetése egy az egyben ráhúzható az igényjog két altípusára, a pozitív és negatív cselekvésekre irányuló igényjogok eseteire. Amíg a pozitív igényjog esetén a partner pozitív cselekvésére (tevésére) irányuló igényről beszélhetünk, addig a negatív igényjog esetén az igény a partner negatív cselekvésére (tartózkodására) vonatkozik. A szabadság esetében is ugyanezt megtehetjük, tehát értelmezhetjük a negatív és pozitív szabadság fogalmát (tevésre és tartózkodásra irányuló szabadságokat értve alattuk), de ez a felfogás teljesen eltér a Berlin-féle értelmezéstől. Meg kell itt jegyeznem azt is, hogy könnyen zavart okozhat az, hogy mind a pozitív és negatív, mind az aktív és passzív minőségeket vonatkoztatjuk a cselekvésekre, és a gyakorlatban nehéz a pontos különbséget tenni köztük, ami sajnos sok félreértésre, félrehasználatra, olykor túlhasználatra ad alkalmat. Ennek oka egyszerű (és érthető): mindkét dichotómia könnyen "ráhúzható" a tevés és tartózkodás kettősségére, hiszen a tartózkodás a tevéshez képest értelemezhető egyfelől negatívnak a pozitívhoz, másfelől passzívnak az aktívhoz képest. Ezen a pongyolaságon nem tudok változtatni. Csak annyit tehetek a potenciális félreértések kizárása érdekében, hogy ebben a könyvben az aktív-passzív jelzőpárost csak a jogra vonatkoztatom, míg a pozitív-negatív minőségeket mind a jog, mind a cselekvés fogalma esetében arra használom, hogy a jog, illetve a cselekvés típusait képezzem a segítségükkel. Ez a kétfajta használat azonban erőteljesen összekapcsolódik, hiszen a pozitív és negatív jog (igény vagy szabadság) altípusait (pozitív, illetve negatív jog) a pozitív vagy negatív cselekvésre (tevésre vagy tartózkodásra) irányultság alapján definiálom.
Az elsőrendű jogviszonyfogalmak formalizálása
A hohfeldi jogfogalmak logikai leírását a skandináv logikai iskola tagjai végezték el a hatvanas-hetvenes években. A legfontosabb szereplője ennek a történetnek Stig Kanger, svéd logikus volt. Ebben a fejezetben Kanger formalizálási kísérletét mutatom be, majd rámutatok arra, hogy bár a Kanger által teremtett formalizmus konzisztens, ezért beemelhetőnek gondolom a társadalmi cselekvés általános modelljébe is, de a kangeri javaslat nem pontosan a hohfeldi fogalmakat ragadja meg. Ezek után megpróbálom korrigálni a kangeri elmélet problémáit, pótolni a hiányosságait. Eközben természetesen többször támaszkodni fogok Kanger követőinek észrevételeire, kritikáira, javaslataira. [♦] Stig Kanger az ötvenes évek végén és a hatvanas években írta meg azokat a tanulmányait, amelyek a hohfeldi jogviszonyok formállogikai feldolgozásával foglalkoztak [StigK] [StigK] [StigK] Kanger első lépésként logikát dolgozott ki a hohfeldi kategóriákra, majd ezekből az elemi jogtípusokból összetett jogtípusokat definiált, amiket atomi jogoknak nevezett el. Mielőtt a kangeri formalizmust bemutatnám, hangsúlyoznom kell, hogy egy szempontból hibásnak tartom Kanger megoldását, amit mindenképpen javítani kell. Kanger ugyanis azzal, hogy egy logikai szintre helyezi el a két hohfeldi jogviszonycsoportot, elfogadhatatlan módon összecsúsztatja azokat, és így nem tudja a felhatalmazottság köré szerveződő jogviszonyfogalmakat jól megragadni. Ez nem azt jelenti, hogy a javasolt formalizmus nem alkalmazható. A logikai struktúra egy az egyben elfogadható és átvehető, csak annyi változtatásra van szükség, hogy a kangeri sémát más fogalmak értelmezésére használjuk. Ebből persze az is következik, hogy mivel a felhatalmazottság körüli fogalomnégyest nem lehet figyelembe venni a kangeri séma interpretációja során, ezekre a fogalmakra új sémát kell kidolgozni. A hohfeldi jogviszonyfogalmak formalizálása és interpretációja előtt Kanger felállít egy logikai elméletet, egy öt axiómából álló sémát, amelyben aztán két operátort definiál. Ezek segítségével fogja majd Kanger a hohfeldi jogfogalmakat meghatározni. Kanger a logikai sémája eredetileg ebből az öt formulából állt.| 1) | $If F \longrightarrow G, then Shall F \longrightarrow Shall G$ | |||||||||||||
| 2) | $(Shall F and Shall G) \longrightarrow Shall (F and G)$ | |||||||||||||
| 3) | $Shall F \longrightarrow not Shall (not F)$ | |||||||||||||
| 4) | $If F \longrightarrow G and G \longrightarrow F, then X causes F \longrightarrow X causes G$ | |||||||||||||
| 5) | $X causes F \longrightarrow F$ | |||||||||||||
| $Shall F $ | = | it shall be that F |
| X causes F | = | X sees to it that (brings about) F holds |
| R(X,Y,F(X,Y)) | $\rightarrowtail$ | $right(Agent,\pm do(Agent,\pm F))$ |
A hohfeldi jogviszonyokat négy egymásra épülő szinten írhatjuk le. Az első szinten az állapotok vannak, a másodikon az események (változások, átmenetek), a harmadikon a cselekvések, a negyediken a jogviszonyok. Az árucserét az állapotszinten úgy írhatjuk le, hogy a kezdőállapothoz képest ($p \land \lnot q \land r \land \lnot s$) a végállapotban minden ellentétébe fordul ($\lnot p \land q \land \lnot r \land s$). A két állapot közti átmenetet az eseményszinten az alábbi formula írja le.
$T(p,\lnot p,e_1)\land T(\lnot q,q,e_1)\land T(r,\lnot r,e_1)\land T(\lnot s,s,e_1)$
| jogosultság | kötelezettség | (= jogosultság tagadása) | ||||||||||||
| right | duty | (= not privilege) | ||||||||||||
| privilege | no-right | (= not right) | ||||||||||||
| power | liability | (= not immunity) | ||||||||||||
| immunity | disability | (= not power) | ||||||||||||
| Hohfeld kategóriái | Kanger kiegészítései | |||||||||||||
| claim | counter-claim | |||||||||||||
| freedom | counter-freedom | |||||||||||||
| power | counter-power | |||||||||||||
| immunity | counter-immunity | |||||||||||||
| claim(Ego,Alter,F(Ego,Alter)) | $shall do(Alter,F(Ego,Alter))$ | |||||||||||||
| counter-claim(Ego,Alter,F(Ego,Alter)) | $shall do(Alter,\lnot F(Ego,Alter))$ | |||||||||||||
| immunity(Ego,Alter,F(Ego,Alter)) | $shall \lnot do(Alter,\lnot F(Ego,Alter))$ | |||||||||||||
| counter-immunity(Ego,Alter,F(Ego,Alter)) | $shall \lnot do(Alter,F(Ego,Alter))$ | |||||||||||||
| power(Ego,Alter,F(Ego,Alter)) | $\lnot shall \lnot do(Ego,F(Ego,Alter))$ | |||||||||||||
| counter-power(Ego,Alter,F(Ego,Alter)) | $\lnot shall \lnot do(Ego,\lnot F(Ego,Alter))$ | |||||||||||||
| freedom(Ego,Alter,F(Ego,Alter)) | $\lnot shall do(Ego,\lnot F(Ego,Alter))$ | |||||||||||||
| counter-freedom(Ego,Alter,F(Ego,Alter)) | $\lnot shall do(Ego,F(Ego,Alter))$ | |||||||||||||
"… Hohfeld fogalmainak pontos meghatározása érdekében a két csoport fogalmai közül igazából csak egyet-egyet kell explikálnunk – az igényjog és a mentesség fogalmait." [StigK]
Ezzel szemben Hohfeld a két csoport "vezérfogalmaként" az igényjogot és a felhatalmazottságot emeli ki. Később fogom elemezni, bemutatni, hogy Kanger miért "tér el" ezen a ponton Hohfeldtől, itt csak annyit vetítek előre, hogy Kanger nem veszi észre, hogy a második hohfeldi jogviszonycsoport tagjait másodrendű fogalmakként lehet megragadni, ezért nem ismeri fel azt sem, hogy az új fogalmaknak kettős öröklődése és így kettős tulajdonsága lesz. A magasabbrendű fogalmiság abban a mozzanatban érhető tetten, ahogy Hohfeld a második jogcsoportot meghatározza. Az első és második jogviszonycsoport abban tér el egymástól – Hohfeld intenciója és meghatározása szerint –, hogy a második esetben a jogviszonyok szűkebb cselekvési tartományra vonatkoznak. Hohfeld a felhatalmazottság fogalmával a jogviszonyok változtatásának lehetőségét, képességét akarta kifejezni, de a többi három új jogfogalom is más jogokra irányuló jogként értelmezendő. A felhatalmazottság és a szabadság egymáshoz való viszonyát tehát más szinten kell kezelni, és nem úgy, ahogy Kanger teszi, amikor a két fogalom közti különbséget a pozitív vagy negatív cselekvések (tevés vagy tartózkodás) hozzárendelésével írja le. Hétköznapi fogalmakra átfordítva Kanger formuláit azt kellene mondanunk, hogy a felhatalmazottság az, ami nem tilos és a szabadság az, ami nem kötelező, de ez egyáltalán nem tűnik intuitívnek. Újra hangsúlyozom: a logikai séma jó, csak az elemeihez fűzött interpretáció nem elfogadható. A megoldás az lehet, hogy Kanger logikai sémáját megtartjuk, de a séma egyes elemeinek interpretálásakor nem alkalmazzuk a hohfeldi másodrendű fogalmakat. Ez azt jelenti, hogy a szabadság, igényjog, felhatalmazottág és mentesség helyett a szabadság és igényjog pozitív, illetve negatív altípusait használjuk a kangeri formulák értelmezéséhez. Ezzel a megoldással megmaradunk az elsőrendű logikai szintjén úgy, hogy a kangeri formalizmus erejét teljes mértékben ki tudjuk használni, így viszont a másodrendű hohfeldi fogalmak kikerülnek a formális modellből, ezért a későbbiekben még ki kell dolgozni az őket leíró formulákat.| positive-claim(Ego,Alter,F(Ego,Alter)) | $shall do(Alter,F(Ego,Alter))$ | |||||||||||||
| counter-positive-claim(Ego,Alter,F(Ego,Alter)) | $shall do(Alter,\lnot F(Ego,Alter))$ | |||||||||||||
| negative-claim(Ego,Alter,F(Ego,Alter)) | $shall \lnot do(Alter,\lnot F(Ego,Alter))$ | |||||||||||||
| counter-negative-claim(Ego,Alter,F(Ego,Alter)) | $shall \lnot do(Alter,F(Ego,Alter))$ | |||||||||||||
| negative-freedom(Ego,Alter,F(Ego,Alter)) | $\lnot shall \lnot do(Ego,F(Ego,Alter))$ | |||||||||||||
| counter-negative-freedom(Ego,Alter,F(Ego,Alter)) | $\lnot shall \lnot do(Ego,\lnot F(Ego,Alter))$ | |||||||||||||
| positive-freedom(Ego,Alter,F(Ego,Alter)) | $\lnot shall do(Ego,\lnot F(Ego,Alter))$ | |||||||||||||
| counter-positive-freedom(Ego,Alter,F(Ego,Alter)) | $\lnot shall do(Ego,F(Ego,Alter))$ | |||||||||||||
| $\b{O} (x do F) $ | $\b{O} (x do \lnot F)$ | $\b{O} (y do F) $ | $\b{O} (y do \lnot F)$ | |||||||||||
| $\lnot \b{O} (x do F) $ | $\lnot \b{O} (x do \lnot F) $ | $\lnot \b{O} (y do F) $ | $\lnot \b{O} (y do \lnot F) $ | |||||||||||
| $\b{O} \lnot (x do F) $ | $\b{O} \lnot (x do \lnot F) $ | $\b{O} \lnot (y do F) $ | $\b{O} \lnot (y do \lnot F) $ | |||||||||||
| $\lnot \b{O} \lnot (x do F)$ | $\lnot \b{O} \lnot (x do \lnot F)$ | $\lnot \b{O} \lnot (y do F)$ | $\lnot \b{O} \lnot (y do \lnot F)$ | |||||||||||
| $(\pm)\b{O}(\pm)\left(\begin{array}{c} X | $\rightarrowtail$ | $(\pm)\b{O}(\pm)\left(\begin{array}{c} Ego | Alter \end{array} \right)do (\pm)F$
Kanger atomi jogtípusai
A jogok tipizálása már Jeremy Bentham számára is fontos volt [LarsL] Bentham három jogtípust különített el, a kötelezés, a tiltás és a nem tiltás és nem kötelezés típusait. Ez a hármas felosztás megfelel a JEPD-elvnek, vagyis a három kategória terjedelme nem fedi át egymást, együttesen viszont kiadják a felettes fogalom (a jog) teljes terjedelmét. A hohfeldi jogviszonyfogalmak nem felelnek meg ennek az elvárásnak. Ezzel tisztában volt Kanger is, ezért a jogfogalmakra JEPD-kompatibilis felosztást dolgozott ki. Kanger kiindulópontja az volt, hogy az általa bevezetett nyolc elemi jogtípus, illetve ezek komplementer párjai összetételével összetett jogi viszonyokat lehet képezni. A hohfeldi-kangeri elemi jogviszonyok összekapcsolásával atomi jogviszonyokat definálhatunk, mégpedig úgy, hogy a 26 egymástól különböző, tehát egymást át nem fedő atomi jogtípus összességében teljesen kitölti a jog fogalmának teljes terjedelmét. Nézzük meg, hogy jutott el Kanger a 26 atomi jogtípusáig. A nyolc elemi összetevőt (a nyolc jogosultságot és kötelezettséget), valamint ezek tagadásait logikailag $2^8$ módon tehetjük össze, így 256-féle, elméletileg lehetséges elemi típusunk (possible atomic types) lehet. Ha ezeket mind feírnánk egy táblázatba, akkor 256 sort kapnánk, és valahogy így nézne ki a táblázat.| 1. | 2. | 3. | 4. | 5. | 6. | 7. | 8. | |||||||
| 1. | claim | freedom | power | immunity | counter-claim | counter-freedom | counter-power | counter-immunity | ||||||
| 2. | claim | not-freedom | power | immunity | counter-claim | counter-freedom | counter-power | counter-immunity | ||||||
| 3. | claim | freedom | not-power | immunity | counter-claim | counter-freedom | counter-power | counter-immunity | ||||||
| 4. | claim | freedom | power | not-immunity | counter-claim | counter-freedom | counter-power | counter-immunity | ||||||
| 5. | claim | freedom | power | immunity | not-counter-claim | counter-freedom | counter-power | counter-immunity | ||||||
| … | ||||||||||||||
| 255. | not-claim | not-freedom | not-power | not-immunity | not-counter-claim | not-counter-freedom | not-counter-power | counter-immunity | ||||||
| 256. | not-claim | not-freedom | not-power | not-immunity | not-counter-claim | not-counter-freedom | not-counter-power | not-counter-immunity | ||||||
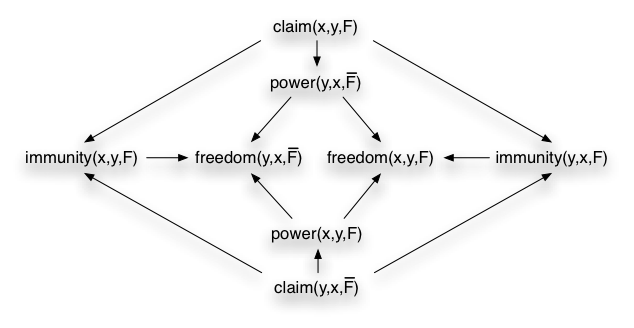
Ha a fenti logikai kapcsolatok miatt mind a 256 sorból elhagyjuk a logikailag fölösleges összetevőket, akkor előfordulhat, hogy kettő vagy több sor meg fog egyezni. A 256 sor eredetileg mind különbözött egymástól, de a "ritkítás" után kevesebb egyedi sort kell kapjunk. Kanger szerint összesen 26 különböző sor marad a végén. Ezeket nevezi Kanger atomi jogtípusoknak. Van olyan sor, amelyben kettő, de van olyan is, amelyben hat elemi jogtípus marad meg. Az atomi jogtípusok és elemi összetevőik listája az alábbi táblázatban olvasható.
| 1) | Power, not immunity, counter-power, not counter-immunity | |||||||||||||
| 2) | Not power, immunity, not counter-power, counter-immunity | |||||||||||||
| 3) | Claim, not counter-freedom | |||||||||||||
| 4) | Not claim, power, immunity, counter-freedom, not counter-power, not counter-immunity | |||||||||||||
| 5) | Power, immunity, counter-power, counter-immunity | |||||||||||||
| 6) | Claim, power, counter-freedom | |||||||||||||
| 7) | Claim, not power | |||||||||||||
| 8) | Power, immunity, counter-freedom, not counter-power, counter-immunity | |||||||||||||
| 9) | Power, immunity, counter-power, not counter-immunity | |||||||||||||
| 10) | Power, not immunity, not counter-power, counter-immunity | |||||||||||||
| 11) | Not freedom, counter-claim | |||||||||||||
| 12) | Freedom, not power, not immunity, not counter-claim, counter-power, counter-immunity | |||||||||||||
| 13) | Freedom, counter-claim, counter-power | |||||||||||||
| 14) | Counter-claim, not counter-power | |||||||||||||
| 15) | Freedom, not power, immunity, counter-power, counter-immunity | |||||||||||||
| 16) | Power, not immunity, counter-power, counter-immunity | |||||||||||||
| 17) | Not power, immunity, counter-power, not counter-immunity | |||||||||||||
| 18) | Not power, not immunity, not counter-power, not counter-immunity | |||||||||||||
| 19) | Not claim, not counter-freedom, not counter-immunity | |||||||||||||
| 20) | Not counter-freedom, counter-immunity | |||||||||||||
| 21) | Not claim, not power, immunity, not counter-power, not counter-immunity | |||||||||||||
| 22) | Power, not immunity, not counter-power, not counter-immunity | |||||||||||||
| 23) | Not freedom, not immunity, not counter-claim | |||||||||||||
| 24) | Not freedom, immunity | |||||||||||||
| 25) | Not power, not immunity, not counter-claim, not counter-power, counter-immunity | |||||||||||||
| 26) | Not power, not immunity, counter-power, not counter-immunity | |||||||||||||
Y has versus X a right of type Q that S(X,Y) míg a konverzió fogalmát az alábbi módon határozza meg: X has versus Y a right of type P that S(X,Y) $\leftrightarrow$
Y has versus X a right of type Q that not-S(X,Y) Kanger a fenti két "korrelativitási" reláció mellé felvesz még egy harmadik relációt, a koordinációt, de ezt itt nem tartom fontosnak bemutatni. Kanger a 26 atomi jogtípust az alábbi ábrába rendezte.
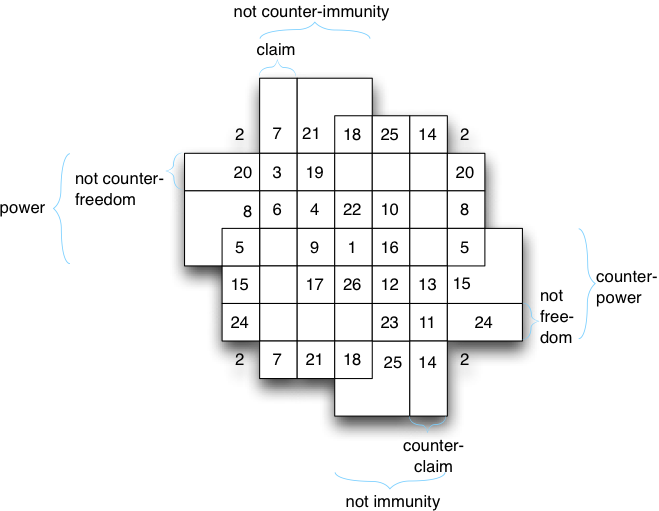
A szokatlan alakú táblázat arra jó, hogy jelezze az egyes kangeri atomi jogtípusok közti kapcsolatokat. A formalizmus alapján pontosan tudható, hogy mely típusok állnak rendre konverz vagy inverz kapcsolatban egymással.
Hohfeld másodrendű jogviszonyfogalmai
A hohfeldi elmélet bemutatásának talán nem "tett jót", hogy nem egyhuzamban mentem végig a hohfeldi kategóriákon, de a logikai építkezés szempontjából rákényszerültem erre. A Kanger által javasolt formalizmust én csak az elsőrendű hohfeldi fogalmakra tartom alkalmazhatónak. Ezért "mozogtam" eddig csak az elsőrendű logikai szinten. A további hohfeldi jogviszonyfogalmak tárgyalásához viszont fel kell majd lépnünk másodrendű fogalmak szintjére, és ez a tény megkívánja (és indokolja is egyben) a két szakaszra osztott tárgyalásmódot. Hohfeld a második – magasabbrendű – jogviszonycsoportba a felhatalmazottság (power), a mentesség (immunity), a beavatkozásnak kitettség (liability) és a beavatkozásképtelenség (disability) kategóriáit sorolta be. Ebben a fogalmi csoportban a felhatalmazottság az a "kulcsfogalom", ami köré a többi három fogalmat szervezve az első csoport esetében megismert struktúrához jutunk újra. A jogi felhatalmazottság a jogi beavatkozásra képtelenség ellentéte és a jogi beavatkozásnak kitettség korrelatív párja. Több részletet is idézek itt, hogy a példák segítségével jobban érthetővé váljék, mit gondol Hohfeld a felhatalmazottságról."Egy meghatározott jogi viszonyban bekövetkező változás fakadhat (1) olyan új tényből, illetőleg ilyen tények együtteséből, amely kívül esik az emberi lény(ek) akaratlagos befolyásán; vagy (2) olyan új tényből, illetőleg tények együtteséből, amely egy vagy több emberi lény akaratlagos befolyása alá esik. Az esetek utóbbi csoportjában az a személy (vagy azok a személyek), aki(k)nek akaratlagos befolyása meghatározó, (jogi) felhatalmazottsággal bír(nak) arra, hogy meghatározott változást idézzen(ek) elő a kérdéses jogviszonyban." [hohfe]
"X fel van hatalmazva arra, hogy hogy Y-ra ruházza érdekeltségét – azaz megszüntesse saját érdekeltségét, és ezzel együtt új és azonos érdekeltséget keletkeztessen Y javára. X tehát felhatalmazottsággal rendelkezik különböző fajta szerződéses kötelezettségek keletkeztetésére." [hohfe]
"A megbízási viszony keletkezése inter alia magában foglalja a jogi felhatalmazottság átruházását a megbízottra, s az ennek megfelelő beavatkozásnak kitettséget a megbízó oldalán. Másként fogalmazva: az egyik fél – P – felhatalmazottsággal rendelkezik arra, hogy megbízotti felhatalmazást hozzon létre a másik fél – A – oldalán, például arra, hogy átruházza P tulajdonát, úgynevezett szerződéses kötelezettséget keletkeztessen P terhére, feloldjon egy P-vel szemben fennálló tartozást, 'megszerezzen' egy tulajdonosi jogcímet P javára, és így tovább." [hohfe]
Bár Hohfeld a definícióban egyértelművé teszi, hogy a felhatalmazottság a jogi viszonyok változtatására irányul, igazából nem – vagy legalábbis nem eléggé – reflektál erre a mozzanatra. Pedig ez az új fogalmi négyes pontos értelmezését tekintve kulcsfontosságú. A felhatalmazottságot és a kapcsolódó másik három jogfogalmat ugyanis nem a logikai minőségét tekintve különíti el Hohfeld az igényjog köré épített fogalmaktól, hanem "csak" a fogalmak értelmezési tartományaiban tesz különbséget közöttük."Míg a joghelyzetek első két párja elsőrendű viszonyt, addig a második kettő másodrendűt képez. Az elsőrendű viszonyok közvetlenül az emberek viselkedésére és kapcsolataira vonatkozhatnak, a másodrendű viszonyok közvetítése nélkül; ezzel szemben a másodrendű viszonyok közvetlenül csak az emberek jogcímeire vonatkoznak, s csak áttételesen (bár meghatározó módon) az emberek viselkedésére és kapcsolataira." [M.H.K]
Magasabbrendű normákról von Wright is ír a normák formális elemzésekor [vonwr] bár ő nem a hohfeldi fogalmak közti viszonyok esetében látja alkalmazhatónak a magasabbrendű logikát. Azt, hogy miként lehet a másodrendű fogalmakat ráhúzni a hohfeldi elméletre, rövidesen bemutatom, de előtte még meg kell ismernünk Hohfeld meghatározásait a felhatalmazottság köré építhető jogviszonyfogalmakra. A jogi felhatalmazottságra ott lehet példákat keresni, ahol jogi viszonyok változtatásáról van szó. Ilyen egy miniszter kinevezése vagy felmentése, ilyen a házasság, az örökbefogadás, a végrendelkezés, az örökség visszautasítása, az elővételi jog gyakorlása, a megbízási érdekek képviselete, az ajánlati kötöttség, a telki szolgalom biztosítása. Minden tulajdonviszony jogszerű változtatását eredményező aktus a jogi felhatalmazottságon alapul. Lehet felhatalmazottságból eredő jogviszonyváltozás az, amikor valaki elcseréli a lakását két másikra vagy eladja a boltját, de a felhatalmazottság megnyilvánulhat abban is, ha a boltos megváltoztatja a nyitvatartási idejét, a tulajdonos bezárja a vendéglőjét vagy valaki lemond valamely tulajdonáról. A felhatalmazottság valamiféle jogosultságot jelent, amivel ha él valaki, akkor a felhatalmazottság tartalma, valamely konkrét cselekvés megvalósul, és ezt a többiek tudománsul veszik, "jogosnak" tartják. Ez természetesen nem jelenti azt, hogy ne lehetne valamely cselekvést megtenni úgy, hogy az embernek nincs rá felhatalmazottsága. Ékes példa erre az alábbi jól ismert történet."Hamrák egy újságban olvasta, hogy Székesfehérvár vezetői megelégelték, hogy a piactéren vagy száll a por, vagy öles pocsolyákban tobzódnak a kofák, és elhatározták, hogy faburkolattal látják el a teret. Emberünk szépen levonatozott Fehérvárra, ahol egy kávéházban elhitette néhány fiatal városatyával, hogy a fa ára történelmi emelkedés előtt áll, ám neki van éppen tizenöt vagonnyi használt fatéglája, amit hajlandó 9000 aranykoronáért eladni. A hálás hivatalnokok rögtön a kezébe is nyomtak ezer aranykoronát előlegként, hősünk pedig már másnap munkásokat toborzott Pesten a Rottenbiller utca faburkolatának felszedésére. A módszer egyszerű, de nagyszerű volt; innen-onnan összeszedett néhány úttorlaszt, amikkel a Baross-térnél és a Lövölde-térnél lezárta az utcát, aztán a munkásokat rászabadította a faburkolatra. (Ekkor még sok helyen a macskaköves megoldásnál sokkal olcsóbb fakockás útburkolatot használták.) Mindenkinek azt mondta, hogy a városvezetésnek dolgozik, mely a faburkolat bazaltkőre cserélése mellett döntött. A munkások hat nap alatt szedték föl a majdnem egy kilométeres útszakasz burkolatát, amit a Kelenföldi pályaudvarnál vonatra raktak és elszállítottak Székesfehérvárra. A legszebb az egészben, hogy az egész művelet alig került 600 aranykoronába, így még az előlegből is maradt, a sikeres üzlet után pedig megkapta Székesfehérvártól a fennmaradó 8000 aranykoronát is." [Akiel]
A történet értelmezésekor azt kell mondanunk, hogy Hamrák úrnak "nem volt felhatalmazottsága" az útburkolat felszedésére, értékesítésére, amit azonban úgy is mondhatnánk, hogy "nem volt megengedve neki" mindaz, amit megtett. Ez a helyettesíthetőség önmagában jelzi, hogy a felhatalmazottságot milyen deontikus logikai fogalomhoz lehet majd kötnünk, de ezt csak a későbbiekben fogom kifejteni. A felhatalmazottság korrelatív párja a beavatkozásnak kitettség (liability) és ellentéte a beavatkozásképtelenség (disability). A beavatkozásnak kitettségre Hohfeld az alábbi példát adja."A Booth v. Commonwealth esetben a bíróságnak Virginia egyik törvényi rendelkezését kellett értelmeznie, mely szerint « minden szabad fehér férfi, aki betöltötte huszonegyedik életévét és nem töltötte be a hatvanadikat, esküdtként köteles közreműködni, az alábbi kivételektől eltekintve» . Világos, hogy e törvény csak beavatkozásnak kitettséget keletkeztetett, nem pedig kötelezettséget. Az beavatkozásnak kitettség, ha kötelezettséget róhatnak ránk. Ez utóbbi csak akkor következik be, amikor felhatalmazottságukkal élve a peres felek és a bíróság tagjai megtették mindazt, ami az esküdt funkciójának ellátására vonatkozó specifikus kötelezettség létrejöttéhez szükséges." [hohfe]
Az esküdtszéki munkában való részvétel mint a beavatkozásnak kitettség hohfeldi mintapéldájával párhuzamba állíthatjuk a katonai szolgálat feltételes kötelezettségét, ami számunkra talán ismerősebb lehet. Ha a beavatkozásnak kitettség a felhatalmazottság korrelatív párja, akkor minden olyan példa, amit a felhatalmazottság esetében adtam meg korábban, adekvát lehet a beavatkozásnak kitettségre is (természetesen az ágensszerepek megcserélésével). A beavatkozásnak kitettség alanyának nem feltétlen jelent hátrányt az a jogviszonyváltozás, amit a partnere okoz felhatalmazottságával élve. Ha valaki lemond a tulajdonáról (mondjuk, az órájáról), amire természetesen fel van hatalmazva, akkor ez a jogviszonyváltozás előnyös lehet mindenki más számára, hiszen ezzel az aktussal bárki szabadságot és felhatalmazottságot nyer arra, hogy eltulajdonítsa az órát [hohfe] Ezt a jelenséget figyelhetjük meg a nagyvárosi lomtalanítások során. [♦] Azzal, hogy a tulajdonosok kiteszik a szükségtelenné vált ingóságaikat (bútoraikat, használt ruháikat, háztartási eszközeiket, limlomjaikat) a közterületre, egyben jelzik azt is, hogy lemondanak e tulajdonaikról, és bárki viheti azokat. Ekkor potenciálisan mindenki beavatkozásnak kitetté válik, ami azt jelenti, hogy mindenkinek tudomásul kell vennie, hogy a kirakott ingóságok fölötti jogosultság megváltozott, és onnantól kezdve bárki eltulajdoníthatja azokat (akár az eredeti tulajdonos is, bár ez nyilván nem valószínű opció). Az már egy másik kérdés, hogy ki lehet az új tulajdonos. Robert Sugden érdekes tanulmánya szerint az ilyen helyzetekben az elsőségnek lehet perdöntő szerepe [Sugde] Ha az eddig bemutatott két fogalmat, a felhatalmazottságot és a beavatkozásnak kitettséget összetevőikre bontjuk (ahogy tettük ezt az igényjoghoz kapcsolódó jogviszonyfogalmak esetében is), akkor a következő táblázathoz juthatunk.| jogosult & jogviszony &cselekvő& \multicolumn{2}{l}{cselekvés}\\ | ||||||||||||||
| Ego | felhatalmazottsága | Ego | eladni Ego telkét | |||||||||||
| Alter | beavatkozásnak kitettsége | Ego | eladni Ego telkét | |||||||||||
"X, egy ingatlan tulajdonosa … fel van hatalmazva, hogy elidegenítse az Y vagy bárki más számára. Ugyanakkor X-et számos mentesség is megilleti Y-nal vagy bárki mással szemben. Y ugyanis képtelen beavatkozni (azaz nincs felhatalmazottsága), amíg érdekeltséget nem szerez önmaga vagy bárki más számára. S ami igaz Y-ra, az hasonlóképpen igaz bárki másra is, aki sajátos keletkeztető tények folytán felhatalmazottságot nem szerez Y tulajdonának elidegenítésére." [hohfe]
A Hohfeld-recepció jóval kevesebbet foglalkozik a mentesség fogalmával a felhatalmazottsághoz képest. A fogalom tartalmát akkor lehet jól megérteni, ha arra fókuszálunk, hogy a mentesség a beavatkozásnak kitettség ellentéte. A diplomáciai mentesség lehet talán a legnyilvánvalóbb példája ennek. A diplomáciai rendszámmal rendelkező kocsikat nem lehet büntetni nyilvánvaló szabálytalanság esetén sem, vagyis nem lehet a használójára, tulajdonosára nézve kötelező jellegű jogi döntést hozni, nem lehet ő(ke)t jogi beavatkozásnak kitenni. A beavatkozás-képtelenség (disability) a felhatalmazottság ellentéte (annak hiánya) és a mentesség korrelatív párja. Példaként lehet hozni rá a hatóságok hatáskörének vagy illetékességének hiányát valamely ügyben, a bérbeadó rendelkezési jogának szűkítését a bérbe adott dolog fölött vagy a rendőr beavatkozásképtelenségét a szabálytalankodó, ám diplomáciai rendszámmal rendelkező autóssal szemben, de idetartozik az is, hogy a tulajdonom fölött más nem rendelkezhet, nem adhatja el, nem használhatja, hacsak én nem adtam erre engedélyt. A mentesség és beavatkozásképtelenség fogalmainak összetevőkre bontása eredményeként az alábbi táblázatot kapjuk.| jogosult & jogviszony &cselekvő& \multicolumn{2}{l}{cselekvés}\\ | ||||||||||||||
| Ego | mentessége | Alter | nem | eladni Ego telkét | ||||||||||
| Alter | beavatkozásképtelensége | Alter | eladni Ego telkét | |||||||||||
| jogosult & jogviszony &cselekvő& \multicolumn{2}{l}{cselekvés}\\ | ||||||||||||||
| Ego | felhatalmazottsága | Ego | eladni Ego telkét | |||||||||||
| Alter | beavatkozásnak kitettsége | Ego | eladni Ego telkét | |||||||||||
| Ego | mentessége | Alter | nem | eladni Ego telkét | ||||||||||
| Alter | beavatkozásképtelensége | Alter | eladni Ego telkét | |||||||||||
| jogosult & jogviszony &cselekvő& \multicolumn{2}{l}{cselekvés}\\ | ||||||||||||||
| Ego | szabadsága | Ego | átjárni Ego telkén | |||||||||||
| Alter | igényhiánya | Ego | nem | átjárni Ego telkén | ||||||||||
| Ego | igénye | Alter | nem | átjárni Ego telkén | ||||||||||
| Alter | kötelezettsége | Alter | nem | átjárni Ego telkén | ||||||||||
"A beavatkozásnak kitettség nem más, mint felelősség." [hohfe]
de ez a mondat nem igazán segíti a tisztánlátást. [♦] A felhatalmazottság és a beavatkozásnak kitettség magyarázata során kétféle értelemben is félrevezetőnek, sőt hibásnak tartom a hohfeldi megközelítést, amit sajnos a későbbi Hohfeld-recepció is folyamatosan életben tartott. Egyfelől ezen a ponton kerül be az nézet a hohfeldi elméletbe, miszerint a felhatalmazottság (illetve korrelatív párja a beavatkozásnak kitettség) nem jogok, hanem kapacitások, képességek létezéséről vagy azok hiányáról szól. Az angol terminusok közül a disability már önmagában is ezt a "sugallja". Ennek kritikájára a következő fejezetben fogok kitérni. Másfelől a felhatalmazottság és a beavatkozásnak kitettség kapacitív fogalmait Hohfeld (és utána még sok más szerző is) úgy értelmezi, mintha abban definitív szerepe lenne a feltételességnek. Megismétlem az előző Hohfeld-idézet egy részletét:"… beavatkozásnak kitettség, ha kötelezettséget róhatnak ránk. Ez utóbbi csak akkor következik be, amikor felhatalmazottságukkal élve a peres felek és a bíróság tagjai megtették mindazt, ami az esküdt funkciójának ellátására vonatkozó specifikus kötelezettség létrejöttéhez szükséges." [hohfe]
Az idézetből úgy tűnik, mintha Hohfeld szerint a beavatkozásnak kitettség feltételes kötelezettség lenne. Ez a feltételesség azonban nem köthető kizárólagosan a beavatkozásnak kitettséghez, előfordulhat az "egyszerű" kötelezettségek esetén is. Ha én – felhatalmazottságommal élve – kölcsönadom valakinek egy könyvemet, akkor folyamatos igényem (a partneremnek pedig folyamatos kötelezettsége) lesz arra, hogy, amikor kérem tőle, adja vissza. Ezt értelmezhetem úgy is, hogy a partnerem folyamatos beavatkozásnak kitettségben van, és csak akkor keletkezik kötelezettsége arra, hogy visszaadja a könyvemet, amikor én – felhatalmazottságommal újra élve – ezt valahogy jelzem felé. Amíg azonban nem kérem vissza, addig csak feltételes, potenciális kötelezettséggel rendelkezik. Az itt jelzett problémákat csak akkor tudjuk megoldani, ha megadjuk a másodrendű fogalmak formális definícióit, és így láthatóvá tesszük egyfelől azt, hogy milyen módon kapcsolódnak, hasonlítanak az elsőrendű fogalmakhoz, illetve másfelől bemutatjuk azt, hogy milyen új vonások felvételével lehet őket saját minőségükben megragadni. A következő fejezetben ezt kísérlem meg bemutatni.A másodrendű jogviszonyfogalmak formalizálása
A felhatalmazottság köré építhető hohfeldi fogalmak eddigi elemzéséből kiderült, hogy (i) ezek a fogalmak másodrendűek, (ii) ellentmondás látszik a passzív vagy aktív jog szerinti osztályozásuk, az igényjog vagy szabadság alá való besorolásuk és a korrelatív kapcsolataik eltérő minősége között, valamint (iii) a feltételesség, az állapot- vagy pontszerűség kérdésében eltérő minőséget lehet érezni a komplementer fogalompárok között. A Hohfeld-recepcióban sokan úgy gondolják, hogy azon az alapon különíthetjük el az első- és másodrendű fogalmakat egymástól, hogy az első csoportot jogosultságnak, a másodikat képességnek (potenciálnak, kapacitásnak) minősítjük. Sok példát lehetne hozni arra, hogy miben különbözik a két hohfeldi jogviszonycsoport egymástól. Makinson azt a példát említi, hogy lehet valakinek megengedett vagy tiltott meztelenül fürdeni a tengerparton, de ettől még nem rendelkezik azzal a felhatalmazottsággal, amely alapján ezen a jogosultságon változtatni tudna (megengedhetné vagy megtilthatná azt) [D.Mak] A különbségek megragadása végett egyes szerzők (például Makinson) az elsőrendű fogalmakat deontikus, a másodrendűeket kapacitív képességeknek nevezik. Amikor Frederic B. Fitch egy 1967-es cikkében Hohfeld fogalmaira ajánl egy formalizmust [Frede] akkor, bár nem mondja ki, de a formalizmusból kiderül, hogy eltérő minőségűeknek tartja Hohfeld első és második jogcsoportjába tartozó fogalmakat. Az igényt, szabadságot, kötelességet és joghiányt deontikus operátorokkal, a felhatalmazottságot és a köré rendezett jogfogalmakat a can operátor segítségével definiálja. [♦] Lars Lindahl is ugyanezt a különbséget tartotta fontosnak." … a felhatalmazottságot inkább képességként, nem pedig engedélyként kell értelmezni, tehát inkább úgy, mint » képes«, nem pedig úgy, mint » szabad« (» can« rather than » may«)." [LarsL]
Makinson figyelmeztet rá [D.Mak] hogy maga Hohfeld is erős analógiát tételezett a deontikus és kapacitív képességek egymáshoz való viszonyának tárgyalásakor, amikor így írt."Ha például a közönséges tulajdonos elidegenítési felhatalmazottságára gondolunk, gondosan meg kell különböztetnünk a jogi felhatalmazottságot, a jogi felhatalmazottság » gyakorlásához« szükséges dolgok megtételének fizikai lehetőségét, s végül e dolgok megtételére irányuló szabadságot, már amennyiben ez a szabadság tényleg fennáll. Lehet, hogy fennáll, lehet, hogy nem. Így, ha X mint egy ingatlan tulajdonosa szerződést köt Y-nal, miszerint ingatlanát nem adja el Z-nek, akkor X-nek a Z javára történő értékesítési felhatalmazottság gyakorlásához szükséges magatartások gyakorlására vonatkozó szabadsága X és Y-on kívül mindenki más között fennáll. Világos azonban, hogy X és Y viszonyában az előbbi nem rendelkezik a kérdéses magatartás tanúsítására vonatkozó szabadsággal, vagy megfordítva: Y-nal szemben az a kötelezettség terheli, hogy ne tegye meg azt, ami felhatalmazottsága gyakorlásához szükséges." [hohfe]
Makinson szerint ez a Hohfeld idézet is azt mutatja, hogy a felhatalmazottság és a szabadság nem mindig "jár együtt". A tézis megerősítésére Makinson hoz egy másik példát. Amennyiben egy egyházi közösségen belül a papok csak akkor adhatnak össze két embert, akik közül az egyik nem az egyházközösség tagja, ha mindketten megígérik, hogy a gyereküket a vallási előírások szellemében nevelik fel, akkor "elválhat" egymástól a szabadság és felhatalmazottság kérdése. Ha ugyanis egy pap úgy végzi el a házassági szertartást, hogy nem kapja meg a két házasulandó fél ígéretét, attól még a szabályosan elvégzett szertartás eredményeként a házasság érvényessé válik. Az pedig már egy másik kérdés, ha a pap utána büntetést kap a feletteseitől, mert nem megengedett dolgot művelt. [♦] Makinson szerint két strukturális különbség is van a deontikus és kapacitív modalitások között [D.Mak] Az egyik különbség az, hogy (i) más következményekkel jár az, ha valaki olyat tesz, amire nem volt jogosultsága, illetve nem volt felhatalmazottsága. A másik különbség pedig (amit Makinson Triponodo elvnek nevezett el) azzal kapcsolatos, hogy (ii) mi történik akkor, ha a megengedés, illetve a felhatalmazottság negatív cselekvésre vagyis tartózkodásra vonatkozik. Nézzük meg egy kicsit alaposabban ezt a két elvet."Amikor végrendelkezünk, akkor a tanúk számát illetően vagy 'eleget teszünk' a Végrendeletekről szóló 1837. évi törvény 9. szakaszának, vagy nem. Ha nem teszünk eleget, akkor okiratunk nem lesz jogokat és kötelességeket teremtő 'érvényes' végrendelet; azaz 'joghatás' vagy 'jogkövetkezmény' nélküli 'érvénytelen' végrendelet lesz. De annak ellenére, hogy érvénytelenné válik, a törvényi rendelkezés be nem tartása nem valamilyen kötelezettség 'megszegése', nem is 'vétség', és zavaró lenne erről ilyen fogalmakban gondolkoznunk." [hart:]
Ha a cselekvő nem rendelkezik felhatalmazottsággal egy adott cselekvésre, akkor nem is végezheti el azt. Formálisan kifejezve ezt (feltételezve, hogy a cselekvések tartománya a jogi viszonyok változtatására van leszűkítve).$\lnot\cpower{power}(Agent,\concept{DO}(Agent,F)) \to \lnot \concept{DO}(Agent,F)$
Makinson-tétel (hun) – Makinson theorem (eng)
Ennek a tézisnek igaz kell legyen a kontraponáltja is.$\concept{DO}(Agent,F) \to \cpower{power}(Agent,\concept{DO}(Agent,F))$
Makinson-tétel kontraponáltja (hun) – contraposition of Makinson theorem (eng)
A fenti állítás úgy interpretálható szabad szöveges formában, hogy ha egy ágens végrehajtott egy cselekvést, akkor hatalma is volt végrehajtania azt. A kérdés itt az, hogy mi az az értelem, ami szerint érvénytelennek kell minősíteni egy cselekvést még akkor is, ha sok szempontból teljesen megegyezik azzal, ami érvényes. [♦] Megítélésem szerint a felhatalmazottságot nem képességként, kapacitásként kell értelmezni, és nem is a feltételesség mentén lehet igazán különbséget tenni a beavatkozásban kitettség és a kötelezettség között. Azok, akik a képeséget, a kapacitív modalitást állították szembe a deontikus modalitással, nem tudtak igazán számot adni arról, hogy milyen ontológiai szerkezetbe, hová lehetne beállítani és milyen formulákkal lehetne megragadni a képességet, kapacitív modalitást leíró operátorokat: a felhatalmazottság leírására Fitch ugyan felvette a can operátort [Frede] de nem definiálta, von Wright [vonwr] Makinson [D.Mak] Bulygin [Eugen] pedig még csak kísérletet sem tett a formalizálásukra. A megoldás annak fel- és elismerésében van, hogy a felhatalmazotság (és a többi "társfogalom") egyfelől másodrendű, másfelől összetett, ún. polihierarchikus fogalom. Érdemes ezt az állítást alaposabban kibontani, és levonni a konzekvenciáit. A felhatalmazottság és a "társfogalmai" a jogviszonyok megváltoztatásával kapcsolatosak, míg az "igényjogi csoport" jogfogalmai bármilyen cselekvésre vonatkozhatnak. Ez nagyon fontos mozzanat, amit pontosan kell értelmeznünk. Ha az új fogalmak (a felhatalmazottság és "társai") csak annyiban térnek el a már bevezetett fogalmaktól (az igényjogcsoportba tartozóktól), hogy az egyik fogalmi összetevőjüket, a cselekvés fogalmát tekintve szűkebb terjedelműek, akkor ez az új fogalmak modellbeli helyét is meghatározza. Az új jogviszonyfogalmak nem az eddig megismert fogalmak szintjén, azokkal mellérendelt viszonyban, hanem alárendelt módon jelennek meg, tehát mind a négy új kategória (a felhatalmazottság, a beavatkozásnak kitettség, a mentesség és a beavatkozásképtelenség) valamelyik igényjogi csoportba tartozó kategória alá rendelt fogalomként (altípusként) értelmezhető. Ezt azt is jelenti egyben, hogy amikor a felhatalmazottságot és a mentességet mint a jogosultságok új típusait akarjuk majd formálisan "definiálni", akkor ezeket a már "meglevő" jogosultságfogalmak, tehát az igényjog és a szabadság fogalmai alá sorolhatjuk csak be. [♦] Ha a másodrendű jogosultságfogalmakat az elsőrendű jogosultságfogalmak alá kell rendelnünk, akkor adódik a kérdés, mi hová tartozik. A válasz közel sem egyértelmű. Azt már említettem, hogy ha az aktív/passzív jogi szempontra figyelnünk, akkor a felhatalmazottságot aktív jognak minősítve a szabadság alárendeltjeként kell értelmeznünk, a mentességet mint passzív jogot az igényjog alá kell besorolnunk. Kanger tipizálási javaslata mögött is ez a megfontolás állhatott (☜) Maga Hohfeld azonban ezt a kérdést másként válaszolta meg." … a felhatalmazottság általában ugyanúgy viszonyul a mentességhez, mint a jog [igény] a szabadsághoz. A jog [igény] mással szembeni pozitív igény, a szabadság pedig valaki más jogával vagy igényével szembeni szabadság. Hasonlóképpen: a felhatalmazottság más jogi viszonyának 'alakítására' irányuló lehetőség; míg a mentesség másvalakinek egy jogviszony 'alakítására' szóló jogi felhatalmazottságától való szabadság." [hohfe]
Az előzőekhez képest pont fordított kapcsolatot tételez Hohfeld, amikor az igényjogot és a felhatalmazottságot, illetve a szabadságot és a mentességet köti össze egymással. Igaz, Hohfeld nem beszél alá-fölérendeltségi relációról, és nem is igazán indokolja meg javaslatát. Mindkét másodrendű kategóriát valamiféle megengedésnek (egyszer lehetőségnek, másszor szabadságnak) tartja. Hart is tartja magát a Hohfeld által javasolt struktúrához (vagyis az igény a felhatalmazottsággal, a szabadságot a mentességel köti össze), de ő megpróbál valamiféle indoklást is adni az összerendelések magyarázatául."A következő lehet az egyesítő mozzanat: a jogrendszer mind a négy esetben kifejezetten elismeri az individuum választását vagy negatív értelemben azáltal, hogy nem akadályozza, nem gátolja meg ebben (szabadság és mentesség), vagy megerősítő értelemben azáltal, hogy joghatást rendel hozzá (igényjog és felhatalmazottság). A negatív esetekben nincs olyan törvény, amely akadályozná az egyént abban a választásában, hogy megtegyen valamit vagy tartózkodjon valamely cselekvéstől (szabadság), illetve mindent változatlanul tartson fent saját jogi helyzetét illetően (mentesség); a megerősítő esetekben a jogrendszer joghatást rendel az egyén döntéséhez, amely alapján valaki másnak meg kell tennie valamit vagy tartózkodnia kell valamilyen cselekvéstől, illetve valaki más jogi helyzete megváltozik." [H.L.A]
Hart egy lépéssel többet tesz meg, mint Hohfeld, amikor rögzíti, hogy az igényjog éa a felhatalmazottság esetében " a jogrendszer joghatást rendel az egyén döntséhez", és ez az a mozzanat, ami összeköti e két jogviszonytípust. Az igényjog esetében egyértelmű, hogy ez a hozzárendelt joghatás a másik fél kötelezettsége valamilyen cselekvésre (valaminek a megtételére vagy valamitől való tartózkodásra),) viszont a felhatalmazottság esetében Hart nem mondja meg pontosan, hogy mi is a hozzárendelt joghatás tartalma. Legalábbis abból, hogy Hart csak annyit mond, hogy ilyen esetekben "valaki jogi helyzete megváltozik", nem lehet egyértelműen kikövetkeztetni, milyen joghatásról is van szó. Ahhoz, hogy az egymással "vitatkozó" osztályozási, alá-fölérendelési javaslatok közti ellentmondást feloldjuk, illetve a harti joghatás valós természetét feltárhassuk, szükségünk van a fogalmak formális leírására. Eddig arról beszéltem, hogy a másodrendű fogalmakat az elsőrendű fogalmak alá kell besorolnunk. Ezt mondhatjuk másként is: Hohfeld első és második jogviszonycsoportjába tartozó fogalmak között generikus alárendeltségi reláció (generic subordinate relation) létezését kell feltételeznünk. [♦] A generikus alárendeltségi viszony lehet polihierarchikus (polyhierarchical), illetve monohierarchikus (monohierarchical) jellegű [Szaka] Előbbi azt jelenti, hogy a leszármaztatott fogalomnak lehet több fölérendeltje is, utóbbi esetben csak egy fölöttes fogalom lehetséges. Amellett fogok érvelni a következőkben, hogy Hohfeld felhatalmazottság fogalma polihierarchikus módon rendelhető mindkét elsőrendű jogviszonyfogalom, a szabadság és az igényjog kategóriája alá. Abból kell kiindulnunk, hogy a felhatalmazottság (és a többi másodrendű fogalom) jogviszonyfogalom. Egy jogviszonyt a következő nyitott formulával írhatunk le.$\concept{RIGHT}(Agent,\pm\concept{DO}(Agent,T_1)) $
elsőrendű jogviszony nyitott formulája (hun) – open formula of first-order right relation (eng)
Amikor – Hohfeld nyomán – a felhatalmazottságot úgy értelmezzük, hogy az jogviszonyok megváltoztatására irányuló jogviszony, akkor ezt úgy ragadhatjuk meg, hogy valamely elsőrendű jogviszony (tehát kétféle szabadság vagy kétféle igényjog, illetve ezek korrelatív kötelezettségpárjai) megváltoztatásának jogát jelenti.$\concept{RIGHT}(Agent,\pm\concept{DO}(Agent,\concept{RIGHT}(Agent,\pm\concept{DO}(Agent,T_1)))) $
másodrendű jogviszony nyitott formulája (hun) – open formula of second-order right relation (eng)
A fenti képletbe ekkor a right helyett power-t írhatunk, az Agent-változó helyébe Ego-t, a $T_1$ helyébe pedig valamely korábbi jogviszony megváltoztatását mint cselekvést helyettesíthetjük.$Change(\concept{RIGHT}(Agent,\concept{DO}(Agent,T_0)))$
jogviszonyváltozás (hun) – change of right relation (eng)
A felhatalmazottság definíciójában már nem kell, hogy szerepeljen a $\pm$ jel a do cselekvésoperátor előtt. Azért nincs rá szükség, mert a felhatalmazottság esetén nincs értelme negatív cselekvésről vagyis a felhatalmazottságtól való tartózkodásról beszélni. Az új paraméterekkel a fenti nyitott és általánosított formula erre a speciálisabb alakra hozható.$\concept{POWER}(Ego,\concept{DO}(Ego,Change(\concept{RIGHT}(Agent,\concept{DO}(Agent,T_0)))))$
felhatalmazottság (hun) – power (eng)
Ez a képlet szemléletesen mutatja a fogalom másodrendű jellegét, hiszen egy jogviszonyba beágyazva egy másik jogviszony szerepel paraméterként. Ezen a ponton viszont fel kell tennünk a kérdést, vajon milyen módon lehetne kifejezni a power fogalmát elsőrendű jogviszonyfogalmak segítségével, vajon a szabadság (freedom) vagy az igényjog (claim) alá tartozik. Az első – kézenfekvőnek tűnő – válasz az kell legyen, hogy a power a freedom alárendeltje, hiszen mindkettő aktív jog, és a felhatalmazottság gyakorlásához valamilyen formában szükséges feltételnek tűnik, hogy a jogbirtokos rendelkezzen a jogviszony változtatásához szükséges szabadsággal. Vélhetőleg ez a szerkezeti hasonlóság vezethette Kangert is arra, hogy a szabadság mellé a felhatalmazottságot emelje be a deontikus logikai sémájába. Bár von Wright elsősorban kompetencianormának nevezte, de ő is permisszív normának minősítette a hatalom/felhatalmazottság fogalmát:"A magasabbrendű kompetencianormákat permisszív normáknak nevezem. Azt mondhatjuk, hogy egy kompetencianorma vagyis egy magasabbrendű permisszív norma kibocsátásának aktusában a magasabbrendű felettes hatóság delegálja a felhatalmazottságát egy alacsonyabbrendű alárendelt hatóság számára. A 'felhatalmazottság' itt nem más, mint 'normával teremtett kompetencia normák kibocsátójaként cselekedni'. Úgy is beszélhetünk erről, mint normatív kompetencia vagy felhatalmazottság." [vonwr]
Észre kell azonban azt is vennünk, hogy van egy másik szerkezeti hasonlóság is a hohfeldi fogalmak között. A szabadság korrelatív párja az igényhiány, aminek a hohfeldi másodrendű fogalmak között a beavatkozásképtelenség felelne meg – miközben Hohfeld a felhatalmazottság korrelatívumára, a beavatkozásnak kitettségre állandóan úgy hivatkozik, mint ami szerkezetileg, deontikus modalitását tekintve a kötelezettségnek felelne meg. A feltételes kötelezettség hohfeldi elképzelése is ezt sugallja. Ha a felhatalmazottság mint speciális szabadság aktív jog, akkor annak korrelatív párjának passzív jognak kéne lenni, viszont a beavatkozásnak kitettség szintén aktív jognak tűnik. Ellentmondásos helyzetnek tűnik, de nem az. A látszólagos ellentmondás feloldódik, ha észrevesszük, hogy a felhatalmazottság fogalmában valójában két elsőrendű jogviszonyt érhetünk tetten. A felhatalmazottság "alapja" az a szabadság, amely "lehetővé teszi", hogy a jogbirtokos megváltoztathasson egy jogviszonyt. De ezzel még nincs vége. A jogbirtokos ezzel párhuzamosan egy igényjoggal is fellép a másik féllel szemben arra vonatkozóan, hogy a partnere ismerje el a jogviszony-változtatás tényét (érvényességét). A beavatkozásnak kitettség az ebben az értelemben vett elismerési igénnyel szembeállítható elismerésére irányuló kötelezettséget jelenti. Ennek az elismerésnek kifejezésére fel kell vennünk a modellbe az elismerés fogalmát, aminek segítségével már a felhatalmazottság fogalmát formális módon is kifejezhetünk úgy, hogy két komponensre bontva írjuk le.$\concept{RECOGNITION}\equiv\concept{RECOGNITION}(\concept{DO}(Agent,T_0))$
elismerés (hun) – recognition (eng)
$\concept{POWER}(Ego,\concept{DO}(Ego,\concept{CHANGE}(\concept{RIGHT}(Agent,\concept{DO}(Agent,T_0))))) \defi$
$\concept{FREEDOM}(Ego,\concept{DO}(Ego,\concept{CHANGE}(\concept{RIGHT}(Agent,\concept{DO}(Agent,T_0))))) \land$
$\concept{CLAIM}(Ego,\concept{DO}(Alter,\concept{RECOGN}(\concept{DO}(Ego,\concept{CHANGE}(\concept{RIGHT}(Agent,\concept{DO}(Agent,T_0)))))))$
felhatalmazottság (hun) – power (eng)
Ez az összetettség azt jelenti, hogy a felhatalmazottság polihierarchikus fogalom, vagyis nem egy, hanem több generikus fölérendelt (generic superordinate) fogalom alá lehet besorolni. [♦] Ha így értelmezzük a felhatalmazottság fogalmát, akkor már magyarázhatóak a korábban jelzett "anomáliák", érthetővé válik a beavatkozásnak kitettség és a kötelezettség oly közeli viszonya is. Ha a felhatalmazottságban van egy igényjogi összetevő, akkor annak korrelatívuma egy kötelezettség lesz, ami a beavatkozásnak kitettség fogalmába "kerül be", és ez a mozzanat alapozza meg a kötelezettség és a beavatkozásnak kitettség fogalmai között érzett hasonlóságot. A felhatalmazottság meghatározásából már könnyen levezethetjük annak inverz fogalmát, a beavatkozásnak kitettséget. A két fogalom közt fennálló inverzitás tényét kihasználva, a beavatkozásnak kitettséget is polihierarchikus fogalomként kell értelmeznünk, csak épp a felhatalmazottsághoz rendelt szabadság és elismerési igényjogi összetevők inverzeit kell a beavatkozásnak kitettség két összetevőjeként definiálni.
$\concept{LIABILITY}(Alter,\concept{DO}(Ego,\concept{CHANGE}(\concept{RIGHT}(Agent,\concept{DO}(Agent,T_0))))) \defi$
$\concept{NO-CLAIM}(Alter,\neg\concept{DO}(Ego,\concept{CHANGE}(\concept{RIGHT}(Agent,\concept{DO}(Agent,T_0))))) \land$
$\concept{DUTY}(Alter,\concept{DO}(Alter,\concept{RECOGN}(\concept{DO}(Ego,\concept{CHANGE}(\concept{RIGHT}(Agent,\concept{DO}(Agent,T_0)))))))$
beavatkozásnak kitettség (hun) – liability (eng)
Kicsit meglepő, de tény, hogy a szakirodalomban a felhatalmazottsághoz képest alig foglalkoztak a mentesség fogalmával. Amennyire "egyenrangúan" kezelték, azaz ugyanakkora figyelemmel kísérték az igényjog és a szabadság kategóriáit, annyira figyelmen kívül hagyták a mentesség fogalmát. Az eddigiek alapján már megadható mind a mentesség, mind a korrelatív párja, a beavatkozásképtelenség formális definíciója, nem érzem szükségét a hosszas magyarázatoknak.
$\concept{IMMUNITY}(Ego,\lnot\concept{DO}(Alter,\concept{CHANGE}(\concept{RIGHT}(Agent,\concept{DO}(Agent,T_0))))) \defi$
$\concept{CLAIM}(Ego,\lnot\concept{DO}(Alter,\concept{CHANGE}(\concept{RIGHT}(Agent,\concept{DO}(Agent,T_0))))) \land$
$\concept{CLAIM}(Ego,\concept{DO}(Alter,\concept{RECOGN}(\concept{DO}(Ego,\concept{CHANGE}(\concept{RIGHT}(Agent,\concept{DO}(Agent,T_0)))))))$
mentesség (hun) – immunity (eng)
$\concept{DISABILITY}(Ego,\lnot\concept{DO}(Alter,\concept{CHANGE}(\concept{RIGHT}(Agent,\concept{DO}(Agent,T_0))))) \defi$
$\concept{DUTY}(Alter,\lnot\concept{DO}(Alter,\concept{CHANGE}(\concept{RIGHT}(Agent,\concept{DO}(Agent,T_0))))) \land$
$\concept{DUTY}(Alter,\concept{DO}(Alter,\concept{RECOGN}(\concept{DO}(Ego,\concept{CHANGE}(\concept{RIGHT}(Agent,\concept{DO}(Agent,T_0)))))))$
beavatkozásképtelenség (hun) – disability (eng)
A jogviszonyfogalmak és szabályfogalmak viszonya
Az eddigiekben jogviszonytípusokról, azok értelmezési lehetőségeiről volt szó, és a deontikus operátorokat használtam a fogalmak formális leírásához. A másodrendű jogviszonyfogalmakkal egy olyan pontra értünk, amikor megpróbálhatjuk hasznosítani azokat az elméleteket, fogalmakat, amelyeket az általában vett szabályok tipizálása során alkottak meg, de ehhez az is szükséges, hogy innentől kezdve az általánosabb szabály fogalomról beszéljünk egy darabig az eddigi jogviszonyfogalmak helyett. A jelen kontextusban a szabály fogalmát a norma fogalmával szinonim módon fogom használni, noha egy végső modellben a szabály főfogalma alá gondolom berendelendőnek a norma alfogalmát. Azt azonban fontos rögzíteni, hogy a szabály fogalmát az egész könyvben az emberi cselekvésekre vonatkozó szabályként használom, ebben az értelemben ez a fogalomhasználat szűkebb jelentésű a teljesen általános szabályfogalomhoz képest (a szabály terminus jelentése tehát ebben a könyvben megegyezik a cselekvési vagy viselkedési szabály fogalmának jelentésével). A cselekvési (viselkedési) szabály fogalmát már sokat használtam, több helyen is elemeztem a könyvemben (☜) illetve (☜) így itt csak egy idézettel szemléltetem, miért is fontos a szabály mind a társadalmi cselekvések végrehajtásában, mind azok magyarázatában."Két jel utal arra, hogy a viselkedés szabályvezérelt, nem pedig csupán rendszeresen ismétlődő: a mintától való eltérést valamiképpen hibának vagy tökéletlenségnek tartjuk, valamint a szabályt automatikusan alkalamazzuk új esetekre is. Ha a cselekvő szembekerül egy új esettel, amellyel korábban nem találkozott, tudni fogja, mit tegyen." [JohnS]
Bár ez a szabályfogalom megengedi, hogy mind a normához, mind a szokáshoz igazodó cselekvésre ráhúzzuk, a továbbiakban csak a normativitás körébe tartozó szabályfogalmakkal foglalkozom. Az egyik fontos megválaszolandó kérdés az az, hogy milyen típusai vannak a viselkedési szabály fogalmának. Eugenio Bulygin miután tisztázza, hogy a szabály (rule) és a norma fogalma között nem tesz különbséget, valamit egymás szinonímájaként használja a kompetencia, kapacitás, potencia, hatalom, uralom, képesség, befolyás teminusokat, két szabályfogalmat különböztet meg egymástól: a viselkedési normák (norms of conducts) és a kompetencianormák (competence norms) kategóriáit [Eugen] Von Wright háromféle normát különít el: (i) a preskripciókat vagy regulációkat (prescriptions, regulations), (ii) a determinatív szabályokat (determinative rules) és (iii) a technikai normákat vagy direktívákat (technical norms, directives) [vonwr] A von wright-i hármas felosztás első két eleme, a preskripciók és a determinatív szabályok megfeleltethetők a harti kettős szabályfelfogásnak, a harmadik von wright-i szabályfogalom, a technikai normák fogalma viszont eltér minden eddigi tipizálási kísérlettől. Sokan mások, én magam sem tartom igazán a norma fogalma alá sorolhatónak ezt a fogalmat, mert pont a normativitáshoz szükséges legfontosabb elem, a szankció hiányzik belőle. Bulygin azt javasolja, hogy von Wright determinatív szabály kifejezése helyett inkább a fogalmi szabályok kifejezést használjuk, és tekintsünk el a harmadik von wright-i normatípustól, majd pedig kijelenti, hogy szerinte a kompetencianormákat nem lehet visszavezetni sem a kötelesség, sem a megengedés fogalmára. A viselkedési norma megsértése esetén szankció várható (következik), ezzel szemben a kompetencianorma megsértésekor érvénytelen lesz a felhatalmazottságot közvetítő, átruházó, deklaráló cselekvés [Eugen] Ha nem az előírt feltételekhez igazodva születik meg valami, akkor érvénytelenség, semmisség (nullity) lesz a következménye ugyanúgy, mint bármely játékban (sakk, sport) ez történik, ha megsértik a játékszabályokat. Így ír Bulygin:" … Hart lényeges pontra tapint rá. Szankció és érvénytelenség [nullity] két radikálisan különböző fogalom és bármely kísérlet, amely beolvasztaná az érvénytelenséget a szankció fogalmába, kudarcra van ítélve. Ráadásul a szankcióra és érvénytelenségre jellemző eltérő működésmódok azt is mutatják, hogy lényegi különbség van a két szabálytípus között is. Első pillantásra a konstitutív szabály az, ami definál egy fogalmat vagy egy játékot mint tevékenységet, és ezáltal értelmessé teszi az érvénytelenségről való beszédet. Ha azonban létezik egy definíció, amely szerint ahhoz, hogy egy norma, egy cselekvés vagy egy dokumentum érvényessé váljék, bizonyos feltételeket ki kell elégíteni, akkor bármely feltétel hiánya az adott norma, cselekvés, dokumentum érvénytelenségét idézi elő. Az érvénytelenség nélkül nem létezik maga a definíció sem, így a konstitutív szabály és az érvénytelenség nem választhatóak el egymástól. E kétfajta intézmény, a büntetés és az érvénytelenség együttes létezése egyben jelzi a jogrendszer (legalább) kétféle szabályának létezését: vannak viselkedési normák és konceptuális szabályok, vagy, mindezt searle-i terminusokban kifejezve, vannak regulatív és konstitutív szabályok." [Eugen]
A regulatív és konstitutív szabályok fogalmainak bevezetését John Searle nevéhez kötik, ami a terminológiai szinten természetesen helyénvaló, de Searle-t jócskán megelőzte John Rawls, aki már 1955-ben szembeállította a summázati és gyakorlati szabályokat egymással úgy, hogy Rawls fogalomkettőse fogalmilag teljesen megfeleltethető Searle párosának [rawls] Searle regulatív szabályai (és Rawls summázati szabályai) olyan cselekvésekre vonatkoznak, amelyek akkor is "léteznének", ha nem irányulna rájuk szabályozás. Ezzel szemben a konstitutív szabályok (Rawlsnál a gyakorlati szabályok) maguk "teremtik", maguk teszik lehetővé a cselekvéseket, az ilyen szabályok híján az ilyen cselekvések nem léteznének, értelmetlenekké, értelmezhetetlenekké válnának. A regulatív szabályok alá sorolható cselekvésekre deontikus operátorok irányulhatnak, és ha a szabályok által előírt cselekvések nem valósulnak meg, tehát "szabálysértés" történik, akkor ezt szankció követi. Ez utóbbi összefüggést lehet kifejezni az alábbi két formulával .$((\concept{OBLIGATORY}(A) \land \lnot A) \veebar (\concept{FORBIDDEN}(A) \land A)) \rightarrow \concept{S}$
regulatív szabály (hun) – regulative rule (eng)
A formulában S a szankciót, A a cselekvést jelöli. A konstitutív szabályok által teremtett cselekvéseket máshogy lehet jellemezni. A konstitutivitás mozzanatát John Searle a counts as (valaminek számít) operátor segítségével véli megragadhatónak, és ezért azt javasolja [JohnS] hogy az alábbi módon értelmezzük a konstitutív szabályt: 'valamely X dolog valamely C kontextuson belül Y dolognak számít'. Ezt felírhatjuk a következő formulába, amit nem igazán minősíthetünk tartalmasnak.`$X$ counts as $Y$ in $C$' $\equiv C \to X \leftrightarrow Y$
konstitutív szabály (hun) – constitutive rule (eng)
A szabálynak formáját tekintve olyan a szerkezete, mint egy új fogalom definíciójának. Az "annak számít" kifejezés helyett mondhatnánk azt is, hogy "definiáljuk úgy, hogy". Y az az új dolog, entitás, amelyet a konstitutív szabály alkalmazása révén konstituálunk, X pedig az a dolog, entitás, amely a szabály alkalmazása nélkül (előtt) is létezik a világban. Utóbbira – Searle terminológiáját használva – a nyers tények (brute facts), előbbire az intézményes tények (institutional facts) vonatkoznak [JohnS] Sokan elfogadták, helyeslően átvették Searle formuláját, és persze voltak, akik kritizálták őt ezért. [♦] Joseph Ransdell egy 1971-es tanulmányában azzal "támadta" Searle-t, hogy az intézményes tényeket "hordozó" entitást kifejező Y terminusban összemos két fontos mozzanatot, amit pedig inkább szét kellene választani, és érdemes lenne külön reprezentálni őket [Josep] Ransdell kritikája annyiban jogos, hogy amikor Searle a fenti formuláról beszél, akkor ahhoz képest szövegszerűen maga is további összetevőkre utal, ám ezeket nem emeli be a formalizmusába. Searle szerint azzal, hogy X-re "mutatva" konstituálunk egy intézményes tényt, miközben "létrehozzuk" Y-t, ez utóbbi terminussal egyben specifikálunk egy új státust is, amihez hozzárendelünk egy vagy több funkciót [JohnR] Ezek a funkciók adják a konstitúció értelmét. Ezek a státusfunkciók (status function) olyan szabályok, amelyek a konstituált új entitásra vonatkozóan rögzítik, hogy mit lehet vagy mit nem lehet tenni velük. Hiába állapítja meg ezeket Searle, a konstitutív szabály formalizmusába már nem emeli át őket. Ransdell azt javasolja, hogy a konstituált új entitás két fontos összetevőjét nevezzük meg, válasszuk el egymástól [Josep] Szerinte ugyanis a konstituált entitásnak (terminusnak) mindig van mellékjelentése, konnotációja (connotation) egyfelől, illetve tartalma (import) másfelől. A baseball szabályain szemléltetve Ransdell a következő példákkal világítja meg a két új fogalom jelentését. Vannak Y-terminusok (Ransdell szavaival: játékterminusok/game-terms), mint Ball (labda), Bat (baseballütő), Pitcher (dobó), Batter (ütő), Catcher (elkapó), Inning (menet) stb. Ezeknek legtöbb esetben van konnotációja és tartalma (import-ja). A Bat konnotációjába tartozik a mérete, formája, felépítése, míg a tartalmával azt lehet rögzíteni, hogy mire lehet, mire kell, mire nem lehet használni: például lehet vele ütni a labdát, de nem lehet vele elgáncsolni a futó játékost. Ransdell fontos felismerése, hogy ez utóbbiak elsőrendű játékszabályok (cselekvési szabályok), amelyek "be vannak ágyazva" a másodrendű konstitutív szabályokba. Jobban meg tudom világítani Ransdell gondolatát, ha a szemléltető példákat a baseball helyett inkább a labdarúgás területéről veszem. A labdarúgás szabályait egy több, mint százharminc oldalas könyvben rögzítik [footb] Ez a szabálygyűjtemény tele van konstitutív szabályokkal. A játék játszhatósága végett mindent pontosan definiálni kell, így meghatározás olvasható arról, hogy mit jelent a 'játékos', 'cserejátékos', 'lecserélt játékos', a 'csapat', a 'labda', a 'pálya', a pályára felfestett 'vonalak' és 'pontok', a 'kapu', a 'leshelyzet', a 'szabadrúgás' stb. fogalma. A játék értelme, célja és ezért központi fogalma a 'gól'. Nézzük meg a meghatározását."Gól akkor van, amikor a labda teljes terjedelmével áthalad a kapuvonalon a kapufák között és a keresztléc alatt, feltéve, hogy a gólt elérő csapat előzően nem követett el szabálysértést." [footb]
A definíció támaszkodik olyan, már előzőleg konstituált fogalmakra, mint a 'labda', 'csapat', 'kapuvonal', 'kapufa', 'keresztléc', valamit 'szabálysértés'. Searle formulája úgy konkretizálható, hogy a C kontextus itt a 'labdarúgást játszani', az Y a 'gól' és az X a fenti definíció szinte teljes egészében. A definíciót természetesen csak úgy lehet pontosan és egyértelműen értelmezni, ha ismerjük a meghatározásba ágyazott további konstutitív fogalmak jelentését is. De azok is mind a searle-i logika mentén határozhatóak meg. Eddig tehát tűnhetne úgy is, hogy Searle leírása megfelelő és elegendő, de ez nincs így. Vannak ugyanis olyan szabályok a labdarúgás szabályrendszerében, amelyek kilógnak a searlei formalizmusból. Nézzük meg a büntetőrúgás (tizenegyes) végrehajtásának szabályait! A szabálykönyv korábbi pontjaiban rögzítették, hogy mi az a tíz 'szabálytalanság', amely esetén 'közvetlen szabadrúgást' kell ítélni a szabálysértő játékos csapata ellen [footb] Ezek alapján lehet bevezetni a 'büntetőrúgás' terminusát. A büntetőrúgás konnotációjáként értelmezhetjük azokat a sorokat, amelyekben segítenek abban, hogyan kell a tizenegyesrúgás fogalmát értelmezni."Büntetőrúgás jár az ellen a csapat ellen, amely elköveti a közvetlen szabadrúgást maga után vonó tíz szabálytalanság valamelyikét a saját büntetőterületén, amikor a labda játékban van." [footb]
Miután megadtuk, hogy mit jelent a büntetőrúgás fogalma, milyen esetben kell büntetőrúgást ítélni egy focimeccsen (tehát hogyan, mikor konstituálódik a fogalom), utána kell megadnunk azt, hogy milyen körülmények között és hogyan kell végrehajtani a büntetőrúgást. Ezektől az előírásoktól lesz, lehet érvényes vagy érvénytelen a tizenegyes végrehajtása. Először megadják a büntetőrúgás során előírt elhelyezkedést."A labdát:
\item a büntetőpontra kell helyezni.
\noindent A büntetőrúgást végrehajtó játékost:\item egyértelműen azonosítani kell.
\noindent A védőcsapat kapusának:\item a kapuvonalon a kapufák közt, a rúgó játékossal szemben kell maradnia a rúgás elvégzéséig
\noindent A többi játékosnak:\item a játéktéren \item a büntetőterületen kívül \item a büntetőpont mögött \item a labdától legalább 9,15 méter távolságra kell elhelyezkedni." [footb]
Az elhelyezkedésre vonatkozó szabályok mind a játékosok cselekvésére irányuló, elsőrendű szabályok, melyek a szokásos módon megragadhatóak deontikus operátorokkal. A következő feltételsorban azt rögzítik, hogy milyen módon lehet magát a büntetőrúgást szabályosan végrehajtani. Ezek a szabályok nyilván a büntetőrúgást végző játékosra vonatkoznak csak.
\item "Miután minden játékos a szabály által előírt helyen tartózkodik, a játékvezető jelt ad a büntetőrúgás végrehajtására. \item A büntetőrúgást végző játékosnak a labdát előre kell rúgnia. \item Nem játszhatja meg ismét a labdát, amíg az egy másik játékost nem érintett. \item A labda akkor van játékban, amikor elrúgták és előre elmozdult." [footb]
Ebben a definíciós részben is kötelezések és tiltások vannak, vagyis itt is alkalmazhatjuk az elsőrendű cselekvésekre irányuló deontikus operátorokat. A szabályok harmadik csoportjában a büntetőrúgással kapcsolatos szabálysértéseket és a rákövetkező büntetéseket kapcsolják össze – egymás után felsorolva azokat az eseteket, amikor a büntetőrúgást végző játékos, a kapus, a rúgást végző játékos csapattársa, a kapus csapattársa, illetve mindkét csapat játékosa vét a szabályok ellen. Ha a támadó csapat játékosa sérti meg a játékszabályokat, akkor a játékvezetőnek az alábbiak szerint kell döntenie."Ha a büntetőrúgást végző játékos … [vagy] a rúgást végző játékos csapattársa sérti meg a játékszabályokat:
\item Ha a labda kapuba jut, a rúgást meg kell ismételni. \item Ha a labda nem jut a kapuba, a játékvezető állítsa meg a játékot, és a mérkőzés a védő csapat javára megítélt közvetett szabadrúgással indul újra arról a helyről, ahol a szabálysértés történt." [footb]
Ha a védekező csapat valamelyik játékosa szabálytalankodik, akkor a bírónak a következőképpen kell eljárnia."Ha a kapus … [vagy] a kapus csapattársa sérti meg a játékszabályokat:
\item Ha a labda kapuba jut, gólt kell ítélni. \item Ha nem jut a kapuba, a rúgást meg kell ismételni." [footb]
Ezek a szabályok rögzítik azokat a szempontokat, amelyek alapján a bíró dönthet az érvényesség-érvénytelenség kérdéséről. Fontos különbség, hogy ezek az előírások a bíró tevékenységére vonatkoznak, míg a korábbiak a játékosok cselekvéseire irányultak. Az, hogy mikor lesz gól a büntetőrúgásból, két tényezőtől függ. Egyfelől attól, hogy szabályos volt-e a büntetőrúgás végrehajtása, másfelől attól, hogy a büntetőrúgás eredményeként a labda bekerült-e a kapuba. Feltételezve, hogy a büntetőrúgásra vonatkozó szabályokat betartotta a rúgó játékos, az érvényesség kérdését "leszűkíthetjük" arra a szabályhalmazra, amely a büntetőterületre való belépés tilalmával kapcsolatos (illetve a gól definíciójára). Az alábbi táblázat mutatja, mi a bíró teendője a különböző esetekben.| belép-e valaki: | a labda a kapuba kerül | a labda nem kerül a kapuba | ||||||||||||
| támadó játékos | a büntetőrúgás megismétlése | közvetett szabadrúgás | ||||||||||||
| védő játékos | gól | a büntetőrúgás megismétlése | ||||||||||||
| mindkettő játékos | a büntetőrúgás megismétlése | a büntetőrúgás megismétlése | ||||||||||||
| senki | gól | nem gól, megy tovább a játék | ||||||||||||
Előfordulhat, hogy az érvényesség fogalma mellett más fogalmat is használatba kell venni. Sok esetben meg kell különböztetnünk egymástól az érvényességi feltételt és az eredményességi feltételt. A különbséget a büntetőrúgás példáján szemléltetve azt mondhatjuk, hogy ha a támadó berúgja a labdát, de szabálytalanság történt, akkor érvénytelen lesz a büntetőrúgás, míg ha a támadó nem rúgja be a labdát és nem történt szabálytalanság közben, akkor érvényes lesz a büntető, de eredménytelen. Végül, ha szabályos körülmények között rúgja be, akkor érvényes és eredményes lesz a tizenegyes. A parlamenti választások alkalmával is van érvényességi, illetve eredményességi feltétel. Az érvényességi feltételként azt lehet kikötni, hogy a szavazók x (például 25) százaléka érvényes szavazatot adjon le. Az eredményességhez az kell, hogy valamely jelölt megkapja az érvényes szavazatok valamilyen többségét (például az első fordulóban a szavazatok abszolút, az esetleges második fordulóban a szavazatok relatív többségét). A labdarúgás példáján láthattuk, hogy a konstitutív szabályokat leírásához nem elégséges a searle-i 'counts as' operátor alkalmazása. A szabályok konstitutív jellegét meg lehet ragadni vele, de logikai formalizmus alapjául nem képes szolgálni. A searlei funkció (vagy a ransdelli import) kiegészítő fogalmának szükségessége pedig arra mutat rá, szükség van arra, hogy elsőrendű regulatív szabályokat kapcsoljunk a konstituált fogalmakhoz (társadalmi intézményekhez). Két kérdést is fel kell itt tenni, amelyekre a válaszokat egymással összekapcsolva lehet megadni: (i) milyen logikai formulákkal ragadhatjuk meg a konstitutív szabályokat; (ii) hogyan kapcsolhatjuk össze a konstitutív szabályokat a felhatalmazottság köré szerveződő jogviszony-kategóriákkal vagyis a másodrendű deontikus fogalmakkal. Először is észre kell vennünk, hogy a játékvezető teendőit másodrendű szabályok írják elő, és így a játékvezető cselekvéseit (döntéseit) is másodrendű cselekvésként írhatjuk le. "Ha a kapus megsérti a játékszabályokat büntetőrúgásnál, de közben kivédi a tizenegyest, akkor a rúgást meg kell ismételni." – szól a bíróra vonakozó szabály. Egy előírásba be van ágyazva egy másik előírás (ami a kapusra vonatkozik): ez egyértelmű jele a másodrendű szabálynak. De milyen másodrendű fogalomról van szó? A választ akkor kapjuk meg, ha a hohfeldi fogalmak segítségével próbáljuk meg jellemezni a büntetőrúgás helyzetét. Mit is jelent a büntetőrúgás? Azt a jogot a támadócsapat számára, hogy egy játékosa egyedül rúghassa kapura a labdát a kapussal szemben (és minden más játékos kötelezettségét arra vonatkozóan, hogy ezt az igényjogban kifejezett cselekvést ne akadályozza). Ha a konstitutív szabályok valamelyikét megsértik a büntetőrúgás során, akkor a bíró hozhat döntés az érvényességre vonatkozóan. Amikor a játékvezető úgy ítél, hogy megismételteti a be nem rúgott büntetőt a védőcsapat szabálytalansága miatt, akkor a támadócsapat büntetőrúgásra vonatkozó jogát teremti újra. Tehát a létező jogviszonyok valamelyikét változtatja meg. Ez azt jelenti, hogy a bíró – a hohfeldi értelemben vett – felhatalmazottsággal rendelkezik. Mivel ez a tézis nagyon fontos mozzanat a gondolatmenetemben, ezért szeretnék még egy példát bemutatni, amikor a labdarúgáshoz képest jóval egyszerűbb versenyről szól, ezért jobban áttekinthetőek a viszonyok a játékban. 200 éves hagyomány az angliai Gloucester városában a Cooper-dombi sajtkergetés. [♦] Hosszú ideig hivatalos sportversenynek számított, ám 2009-ben visszavonták a hivatalos minősítést a rendezvénytől a sok balaset miatt. Azóta "nem hivatalosan" gyűlnek össze az évente megrendezett versenyen a versenyzők, nézők. A versenyen a gloucesteri domboldal tetejéről legurítanak egy 3 és fél kilós kerek sajtot, és a résztvevők közül az lesz a nyertes, aki utoléri, és el tudja kapja a sajtot. Ha ilyen nincs, akkor az nyer, aki legelőbb leér a domb aljára. A verseny célja a sajt megszerzése, de ezt gyakorlatilag lehetetlen teljesíteni, tehát a győzelem igazi feltétele a leérés elsősége. A sajtkergetési versenyt mint társadalmi intézményt az alábbi – searle-i értelemben vett 'counts as' – konstitutív szabályokat révén definiálhatjuk.
| Y | (is counted as) X | |||||||||||||
| versenynap | meghirdetett dátum | |||||||||||||
| startvonal | Cooper-domb teteje | |||||||||||||
| célvonal | Cooper-domb alja | |||||||||||||
| pálya | startvonal és célvonal közti terület | |||||||||||||
| sajt | hivatalosan kijelölt sajt | |||||||||||||
| kezdés | elindítják a sajtot a startvonaltól a dombon lefelé | |||||||||||||
| verseny | kezdés után (elkapni a sajtot vagy végigmenni a pályán) | |||||||||||||
| győzelem | versenyen elsőre (elkapni a sajtot vagy végigmenni a pályán) | |||||||||||||
| előírások | szabálytalan/érvénytelen | |||||||||||||
| rajtvonal mögül kell indulni | ha valaki lejjebb indul | |||||||||||||
| kezdés előtt tilos indulni | ha valaki előbb indul | |||||||||||||
| a hivatalos sajtot kell elkapni | ha valaki a saját sajtját kapja el | |||||||||||||
| versenynapon kell versenyezni | ha valaki más napon versenyez | |||||||||||||
"Az egyoldalas " … írásbeli magánvégrendelet alaki szempontból érvényes, ha készítésének ideje az okiratból kitűnik, továbbá ha a végrendelkező azt
\textbf{a)} sajátkezűleg írt végrendelet esetén elejétől végéig maga írja és aláírja;
\textbf{b)} más által írt végrendelet esetén két tanú együttes jelenlétében aláírja, vagy ha azt már aláírta, az aláírást két tanú előtt, azok együttes jelenlétében a magáénak ismeri el, és a végrendeletet mindkét esetben a tanúk is – e minőségük feltüntetésével – aláírják; vagy
\textbf{c)} a sajátkezűleg írt vagy más által írt végrendeletet aláírja, és akár nyílt, akár zárt iratként a közjegyzőnél – végrendeletként feltüntetve – személyesen letétbe helyezi." PTK 7:17. § Az írásbeli magánvégrendelet alaki érvényességi feltételei
[hunpt]
"Borbély József végre elkezdi a beszédét. Elmeséli, hogy ő volt a Tempó, vagyis Tiszta Energiával Magyarországért nevű párt elnöke, mígnem 2009. június 13-án hajnalban 'arra nem ébredtem, hogy Magyarország királyság.' Bármelyikünket megzavarna egy ilyen hír, de Borbély dicséretesen hamar ráeszmélt arra, hogy nemcsak királyság van, de pont ő az 'önkéntes kormányzó'. … 2011. november 11-én véget ért a kettős hatalom időszaka, a Kormányzó visszahelyezte jogaiba az Apostoli Magyar Királyságot, Orbán Viktor pedig azóta nem más, mint egy amúgy is illegitim párt elnöke. … December 28-án Kecskeméten a Kormányzó felavatta az Apostoli Magyar Királyság Kormányzói Hivatalát, egyben betiltotta minden magyarországi párt működését. Ha ez nem lett volna elég, idén február 25-én partra szállt Visegrádon és bátor gerillaakcióval levonta a köztársasági zászlót." [Azapo]
Lehet azt mondani a történet főszereplőjére, hogy "bolond", de ez nem változtat azon a tényen, hogy a hír egy olyan elismerési igény kinyilatkoztatásáról (is) szól, amelyet kevesek azért csak elfogadtak. [♦] Az eddigi fogalmainkat egy táblázaton belül ábrázolva szemléletesebbé tehetők az egyes kategóriák közti szerkezeti hasonlóságok.| kötelező | obligatory$(Ego,$do$(Ego,F)) $ | $\land$ | $ \lnot $do$(Ego,F)$ | $\rightarrow $ | S | |||||||||
| tiltott | forbidden$(Ego,$do$(Ego,F)) $ | $\land $ | do$(Ego,F) $ | $\rightarrow $ | S | |||||||||
| opcionális | optional$(Ego,$do$(Ego,F))$ | $ \land $ | do$(Ego,F) \mid \lnot$ do$(Ego,F) $ | $\rightarrow $ | $\lnot$ S | |||||||||
| megengedett | permitted$(Ego,$do$(Ego,F))$ | $ \land $ | do$(Ego,F) $ | $\rightarrow $ | $\lnot$ S | |||||||||
| mellőzhető | omissible$(Ego,\lnot$ do$(Ego,F))$ | $\land $ | $ \lnot do$(Ego,F) $ | $\rightarrow$ | $ \lnot$ S | |||||||||
| felhat.-tt | authoritative(do$(Ego,F))$ | $\rightarrow$ | $\lnot$ F | |||||||||||
| szabadság | optional$(Ego,$do$(Ego,F))$ | $ \land $ | do$(Ego,F)$ | $\rightarrow $ | $\lnot$ S | |||||||||
| igény | obligatory$(Alter,R(F)) $ | $\land$ | $ \lnot$ do$(Ego,R(F))$ | $\rightarrow $ | S | |||||||||
| nem felhat. | $\lnot $authoritative$(F)$ | $\rightarrow$ | $\lnot$ F | |||||||||||
| szabadság | optional$(Ego,F)$ | $ \land $ | do$(Ego,F)$ | $\rightarrow $ | $\lnot$ S | |||||||||
| igény | obligatory$(Alter,R(F)) $ | $\land$ | $ \lnot$ do$(Ego,R(F))$ | $\rightarrow $ | S | |||||||||
| jogviszony | tartalom | jogkövetkezmény | ||||||||||||
| tilos a dohányzás | cigizem kocsmában | kötelező a szankció | ||||||||||||
| megengedett a dohányzás | cigizem otthon | tilos a szankció | ||||||||||||
| kötelező büntetni | cigizem kocsmában, rendőr büntet | érvényes a szankció | ||||||||||||
| tilos büntetni | dohányzom otthon, rendőr büntet | érvénytelen a szankció | ||||||||||||
| felhatalmazott később nyitni | később nyitok | érvényes | ||||||||||||
| felhatalmazott pénzt nyomni | pénzt nyomtat | érvényes | ||||||||||||
| nem felhat. pénzt nyomni | pénzt nyomtat | érvénytelen+szankció | ||||||||||||
| felhatalmazott lemondani | kiteszi a fotelét lomtalanításkor | érvényes | ||||||||||||
| nem felhatalmazott eladni | eladja a Rottenbiller utca burkolatát | érvénytelen+szankció | ||||||||||||
| felhatalmazott összeadni | anyakönvvezető összeadja a feleket | érvényes | ||||||||||||
| felhatalmazott végrendelkezni | tanuk nélkül írja meg | érvénytelen | ||||||||||||
| nem felhatalmazott kinevezni | kinevezem a minisztert | érvénytelen | ||||||||||||
A jogviszonyfogalmak teljes logikai rendszere
A jog és kötelezettség fogalmainak hohfeldi "finomszemcsés" felbontása "megkívánja" a fogalmak osztályozását, tipizálását. A logikai rend alapján már utaltam egy fontos tipizálási lehetőségre: a hohfeldi jogfogalmakat két típusba rendezhetjük aszerint, hogy első- vagy másodrendű fogalmak-e (elsőrendű jogosultságfogalom a jogigény és szabadság, másodrendű a felhatalmazottság és mentesség). A logikai rend alapján történő megkülönböztetés melletti további tipizálási lehetőségek az aktív és passzív jog, valamint a pozitív és negatív jog megkülönböztetésén alapulnak. A logikai rend, illetve az aktív-passzív dimenzió alapján a négy jogosultságtípusunkat az alábbi módon rendezhetjük el.| aktív jog | passzív jog | |||||||||||||
| elsőrendű jog | szabadság | igényjog | ||||||||||||
| másodrendű jog | felhatalmazottság | mentesség | ||||||||||||
| aktív jog | passzív jog | |||||||||||||
| pozitív jog | pozitív szabadság | pozitív (igény)jog | ||||||||||||
| negatív jog | negatív szabadság | negatív (igény)jog | ||||||||||||
| pozitív jog | pozitív felhatalmazottság | pozitív mentesség | ||||||||||||
| negatív jog | negatív felhatalmazottság | negatív mentesség | ||||||||||||
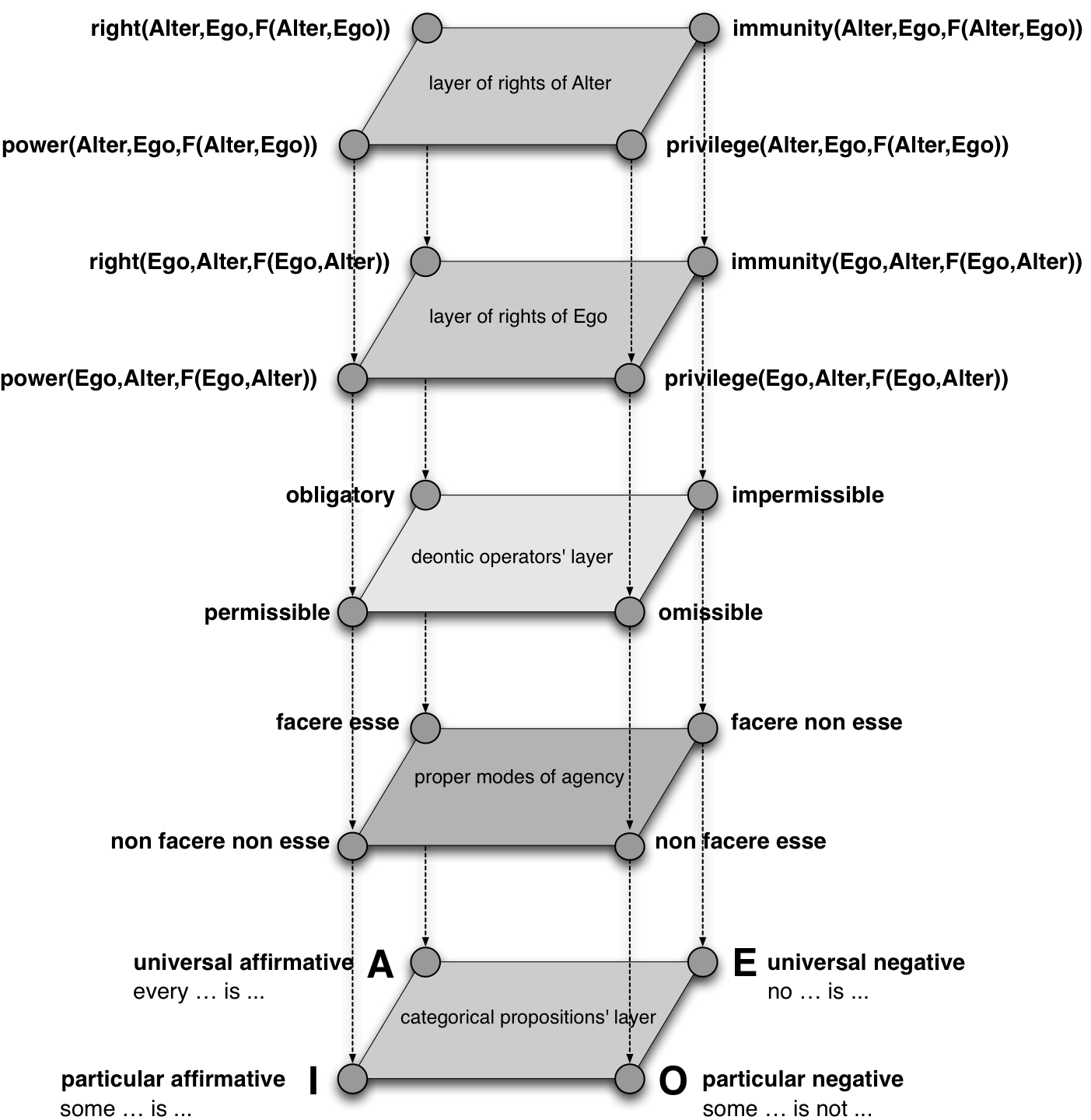
A hohfeldi jogtipológia ugyan nem a JEPD-elvnek (☜) megfelelően különíti el egymástól a négy jogtípust, hiszen nem egymást kölcsönösen kizáró jelentést rendelhetünk hozzájuk, ám ettől még jól megkülönböztethető egymástól a négyféle jogfogalom. A jog terminusában sűrűsödő négyféle jelentésréteg elkülönítése egymástól semmiképpen sem jelenti azt, hogy ezeket csak "magukban" lehetne a tényleges joggyakorlatban jogfogalmainak (tulajdonjog, birtokjog, szerzői jog, vallásszabadság, szólásszabadság stb.) meghatározásához használni. A hohfeldi jogfogalmak segítségével "összetett jogosultságokat" is definiálhatunk. A tulajdonjog példáján kiválóan lehet ezt szemléltetni.
| Ego privilégiuma | Ego birtokolja, használja, hasznosítja saját tulajdonát, hasznot szed belőle | |||||||||||||
| Ego igénye | Alter önhatalmúlag nem birtokolja, nem használja, nem hasznosítja Ego tulajdonát, nem szed hasznot belőle | |||||||||||||
| Ego felhatalmazottsága | Ego rendelkezik a saját tulajdonával (eladja, elcseréli, elajándékozza, haszonbérletbe adja, végrendelkezik vele) | |||||||||||||
| Ego immunitása | Alter nem rendelkezik Ego tulajdonával (nem adja el, nem cseréli el, nem ajándékozza el, nem veszi haszonbérletbe, nem végrendelkezik vele) | |||||||||||||
A jogviszonyfogalmak kiterjesztése
A jogviszonyok eddigi tárgyalása során jogelméleti szerzők gondolataira támaszkodtam. Ez gyakorlati szempontból talán érthető, hiszen ezen a tudományterületen született a legtöbb elemzés e kérdés kapcsán, elméletileg azonban megalapozatlan ez a leszűkítő tárgyalásmód. Az lett volna pontos (és, tán, a helyénvaló), ha a 'jogszonyok' fogalma helyett mindvégig a 'normatív viszonyok' kifejezést használtam volna, de ettől azért tekintettem el, mert nagyon nehézkesnek, kicsit elidegenítőnek, "kontextusvesztőnek" éreztem volna egy jogelméleti gondolatmenet során. A továbblépéshez azonban érdemes ezt az általánosítást megtenni, mert ezzel mód nyílik arra, hogy egyrészt más tudományterületek tudását hasznosíthassuk, másrészt megpróbálkozhatunk azzal, hogy a jogviszonyok elemzése során eddig elért eredményeket máshol is hasznosíthassuk. Az első lépést még egy jogász, Frederick Schauer "segítségével" tehetjük meg. Schauer ugyanis – szigorúan jogelméleti kérdéseket tárgyalva – az intézményeket az általuk hozható döntések típusai alapján különíti el egymástól."Maga a hatáskör fogalma adja azt a hasznos eszközt, mely segítségével különbséget tehetünka döntéshozásra adott felhatalmazás és a meghozott döntés tartalma között. Következésképpen kétféle döntéshozó intézményt különböztethetünk meg: egyfelől azokat, melyek rendelkeznek mind a hatáskörrel felruházó, mind a döntések eredményét meghatározó tartalmi szabályokkal; másfelől pedig azokat, melyek csak az előbbi csoportba tartozó szabályokkal rendelkeznek, s így az eredmény meghatározását a döntéshozó szabályok által nem vezérelt mérlegelésére bízzák." [Frede]
Azért fontos Schauer megkülönböztetése, mert azáltal, hogy az intézményekhez rendelt jogviszonyok – jogelméleti – tárgyalását "áthelyezzük" egy döntéshozatali – szociológiai – kontextusba, láthatóvá, elemezhetővé válhatnak az eltérő jogosultságokkal való rendelkezés szociológiai konzekvenciái. Minden intézményt jogosultságok és kötelezettségek adott rendszerével jellemezhetünk, és minden intézményben a rá jellemző jogviszonyrendszer határozza meg azt, hogy miként cselekszenek, cselekedhetnek a szereplők. Ezek a cselekvések a szereplők döntésein keresztül is értelemezhetők, tehát a döntési kompetenciák különbségei határozzák meg az intézmények közti különbségeket."Azokban a döntéshozó intézményekben azonban, melyekben csak hatáskört megállapító felhatalmazó szabályokat alkalmaznak, hiányoznak a döntések kimenetelét megszabó tartalmi korlátok. A döntéshozó felhatalmazása szélesebb annál, semhogy egyszerűen szabályokat kelljen alkalmaznia a konkrét esetekre. A társadalmi és morális elvek és célkitűzések [policy] teljes készletére támaszkodva kell eldöntenie, hogy mi a teendő az előtte álló konkrét esetekben." [Frede]
Schauer szemléletes példája a rendőr "intézménye", akinek a cselekvését felhatalmazó és tartalmi szabályok egyaránt meghatározzák (Schauer tartalmi szabályon a regulatív szabályokat "érti", bár erre nem igazán reflektál). A kétféle szabály közti viszonyra fény derül az alábbi idézetből."Az a szabály, mely felhatalmaz egy rendőrt arra, hogy mindazokat, de csakis azokat beidézze, akik átlépték az óránkénti kilencven kilométeres sebességhatárt, példaként szolgálhat arra az esetre, amikor a hatáskört megállapító felhatalmazó szabály és az eredményt meghatározó tartalmi szabály együttesen van jelen. Bár a rendőr fel van hatalmazva arra is, hogy idézést adjon ki, s arra is, hogy megállapítsa az autók sebességét, nincs felhatalmazva sem annak meghatározására, hogy mennyi legyen a megengedett legnagyobb sebesség, sem annak meghatározására, hogy mikor mentesülhet valaki a következmények alól, amennyiben átlépte a sebességhatárt." [Frede]
Attól a pillanattól kezdve azonban, amikor már nem jogokról, hanem döntésekről, társadalmi intézményekről beszélünk, hirtelen "kinyílik" a fogalmi, elemzési tér, és a jogrendszeren kívüli normativitásban is ugyanúgy alkalmazhatjuk ezeket a distinkciókat. Nemcsak a döntéshozati jogosítványok alapján megkülönböztetett intézményfogalmakat, hanem minden más, a jogviszonyokról eddig bemutatott fogalmakat is alkalmazhatunk azokon a területeken, ahol jogosultságokról, kötelezettségekről általában beszélhetünk. A jog mint jogrendszer fogalma felől az általánosabb norma fogalma felé elmozdulva más dimenziókba léphetünk át. Bár Somlai Péter a családon belüli társadalmi kapcsolatok világát elemezte "csak", az alábbi meglátása általánosítható mindenféle normatív cselekvést vizsgáló tudományos tevékenység számára."A célracionális cselekvések modelljeivel dolgozó kutatónak tehát nemcsak vágyaktól és szokásoktól, értékvezérelt vagy irracionális döntésektől kell elvonatkoztatnia. Mindezekkel elvonatkoztat a szabályalkotás és intézményesedés folyamataitól is. Attól tehát, hogy (a) lehetnek olyan szabályok, amelyek valamiképp hozzáférhetők a résztvevők számára (akik formálhatják ezeket, illetve felismerhetik érvényességükben a saját kompetenciájukat, jogaikat és felelősségüket) és (b) a szabályok és intézmények is változhatnak a szereplők kapcsolatának és konfliktusainak eredményeként." [Somla]
Bármely társadalmi intézményben, ahol normák szabályozzák a résztvevők cselekvéseit, a kétféle szabály- vagy jogfogalom elemzése adhatja az eszközt az intézményen belüli dinamikák megértéséhez. A jogrendszert elemezve tudtuk az alapvető jogviszonyfogalmakat értelmezni, pontosan definiálni, de ezek a fogalmak – kellő általánosítás után – sok más területen is használhatók. Mindenhol, ahol társadalmi intézményekben emberek saját normatív viszonyaikat próbálják meg szabályozni, fenntartani, változtatni. Vagyis mindenhol, ahol emberek cselekszenek. Pamela Oliver is tett utalást arra, hogy a társadalmi ösztönzők – többek között – arra is alkalmasak, hogy az emberek saját cselekvéseit befolyásoló, jogulstásokkal, kötelezettségekkel teli társadalmi környezetüket megváltoztathassák."Az a lehetőség teszi a szelektív ösztönzőket a kollektív cselekvés dinamikus folyamatainak oly' fontos részévé, hogy megváltoztathatjuk azokat a paramétereket, amelyek meghatározzák mások (és akár sajátmagunk) viselkedését. Az emberek számára nem az az egyetlen lehetőség, hogy reagáljanak saját helyzetükre. Tehetnek is azért, hogy maga a helyzet változzon meg, amely addig korlátozta saját választásaikat." [olive]
Az nyilván nem véletlen, hogy Hart híres másodrendű szabályai között is megtalálhatjuk a változtatási szabályokat (az elismerési szabályok és ítélkezési szabályok mellett) [hart:] hiszen ezek teszik lehetővé egyáltalán a jogszabályok változtatását. De ha a jog egészén mint a normatív rendszerek egy típusán belül szükséges valamely mechanizmus, valamilyen eszköz magának a jogrendnek a változtatásához, akkor ezt nyilván minden más normatív rendszeren (a konvencionális vagy erkölcsi rendszerken) belül is ugyanúgy meg kell találnunk. Nem is kockáztatunk túl sokat, ha azt mondjuk, hogy a magasabbrendű jogosultságokat és kötelezettségeket a társadalmi kapcsolatok dinamikáját biztosító eszközök közé kell sorolnunk. Talán mint a legfontosabbakat.Társadalmi szerep
A hohfeldi jogosultságelmélet logikai formalizmusának kidolgozása után és alapján elég nyilvánvaló volt, hogy ki kellene, ki lehetne dolgozni a társadalmi pozíciók formális elméletét. Mivel azonban nem társadalomtudósok, hanem logikusok, mérnökök álltak neki ennek a feladatnak, ezek a kísérletek nem kapcsolódtak, nem tudtak kapcsolódni a társadalomtudományokban sokféle szempont szerint elemzett, alaposan kiformált társadalmi pozíció-, státus-, szerep- és hatalomelméletekhez. [♦] Pedig lett volna hová. Arra itt nem vállalkozom, hogy bemutassam mindazokat az elméleteket, amelyeket kidolgoztak a társadalomtudomány jeles képviselői a jelzett fogalmakkal kapcsolatban. Egyetlen gondolati ívet szeretnék csak felvázolni, mégpedig azt, amin keresztül össze lehet kötni Hohfeld jogi pozíciókra vonatkozó elméletét a cselekvéselmélet számára különösen fontos uralomelmélettel. Úgy látom ugyanis, amit a könyvem egyik fontos tézisének is tartok egyben, hogy az ontológiai leszármaztathatóság, levezethetőség értelmében, a formális modellépítés szempontjából a jogosultságokra és kötelezettségekre alapozott pozíció fogalma megelőzi a cselekvéselmélet két kiváltképp fontos fogalmát, a norma és az uralom kategóriáját. Hohfeld azt írta le az elméletében, ahogy az által elkülönített jogosultság és kötelezettségtípusok egymással korrelatív kapcsolatban állnak. Itt azonban megállt, és nem vizsgálta tovább, hogy lehet-e még mondani valamit az egymással korrelatív viszonyban álló jogi pozíciókról. Elsőként Sir David Ross [ross:] majd őt követve Alvin W. Gouldner [gould] volt az, aki felfedezte és a társadalomelméleten belül a megfelelő helyére tette a komplementaritás fogalmát. [♦] Gouldner számára az volt az igazi kérdés, hogy a reciprocitás fogalmát hogyan kell értelmezni, és azon belül is különösen az érdekelte, hogy mi a különbség a reciprocitás és a komplementaritás fogalmai között [syiDi] A reciprocitás itt nem annyira fontos, így nyilván a két fogalom viszonya sem érdekes, viszont a gouldneri komplementaritás fogalma annál inkább. Ez a fogalom jelentését tekintve megfeleltethető a hohfeldi korrelativitás kategóriájának vagy a kangeri inverzitás-konverzitás fogalomkettősnek. Ettől persze még nem lenne fontos. A változást és az újdonságot Gouldnernél az jelentette, hogy a komplementaritás fogalmát, illetve a terminussal megragadható jelenséget – tulajdonképpen öntudatlanul – belehelyezte a cselekvéselmélet kellős közepébe azzal, hogy úgy kezelte, mint amivel sok esetben magyarázatot lehet adni a társadalmi cselekvéseink szabályszerűségére. Amikor ugyanis a reciprocitást a komplementaritás kategóriájával állította szembe, akkor a komplementaritás fogalmát vizsgálva a társadalmi szerep fogalmát is elemezte egyben. A társadalmi szerep viszont nem más, mint jogosultságok és kötelezettségek összekapcsolása úgy, hogy egy másik szerephez, a komplementer társadalmi szerephez a komplementer kötelezettségek és jogosultságok vannak hozzárendelve. Vegyünk egy egyszerű példát! Az egyetemen a tanári szerepet egy sor jogosultság és kötelezetség hozzárendelésével határozhatjuk meg. A tanárnak kötelesége órát tartani, tanévkezdéskor be kell jelentenie, mikor lesz zárthelyi a félévben, joga van zárthelyit megíratni a bejelentett napon, joga van rászólni a fegyelmezetlenkedő hallgatóra stb. Ezzel szemben a hallgatói szerephez az tartozik hozzá, hogy joga van órákra járni, joga van tanévkezdéskor rákérdezni, mikor lesznek a zárthelyik, viszont kötelessége beszámolót írnia az adott napon, és szót kell fogadnia a tanár felszólításának. A két társadalmi szerep között igazi komplementaritás létezik. Ami az igazán lényeges itt: nem pusztán az egyes jogosultság- és kötelezettségpárok vannak korrelatív, komplementer viszonyban egymással, de a szereppárok is. Nincs hallgatói szerep a tanári szerep nélkül és fordítva. Tanárként nem állhatok meg a villamoson diákkorú emberek előtt, hogy vegyenek elő papírt, mert lediktálom a zárthelyi dolgozatuk kérdéseit. Ha ezt tenném, értetlenség, kiröhögés várna rám. De nem teszem, mert tudom, hogy a villamoson nem lesznek ott azok, akik a hallgatói szerepben lehetnének, vagy ha netán ott lennének, akkor sem akarnának a hallgatói szerephez igazodni. A cselekvéselmélet számára ez nagyon fontos előrelépés, mert amíg a hohfeldi fókusz a jogi pozíciókon volt, addig nem lehetett az elméletét hatékonyan alkalmazni a tényleges társadalmi cselekvések leírására. A jogi pozíciók túlzottan elemi szintjét jelentik a cselekvéseinknek. Szükség volt és szükség van a hohfeldi alapokra, de szükség volt egy szinttel feljebb lépni, szükség volt arra az általánosításra, amit a társadalmi szerep fogalma hoz(hat)ott el. Ezen a szinten már olyan fogalmakat képezhetünk, amelyek a mindennapi társadalmi gyakorlatban is kezelhető, beazonosítható, kommunikálható szabályszerűségeket ragadnak meg. Azt mondani, hogy tanár, diák, rendőr, eladó, sofőr, gyalogos, anya, gyerek stb., ezek mind olyan szabályszerűségekre mutató fogalmak, amelyeket könnyen és gyakorta felismerhetünk az életünkben. De ennek az a feltétele, hogy minél több, egy adott helyzetekre jellemző jogosultságot és kötelezettséget tudjunk egy komplementer szereppárhoz hozzárendelni. Van még egy további nagyon fontos érv arra vonatkozóan, hogy miért is fontos a társadalmi szerepeknek ez az összekapcsolódása. Talcott Parsons egyik észrevétele érdemes itt felidézni [parso] Parsons úgy érvelt, hogy a komplementer szerepek egyik legfontosabb funkciója az, hogy békés úton old meg egyébként eredetileg, önmagában véve konfliktusos társadalmi kapcsolatokat. Mindegyik társadalmi szerepet betöltő fél számára sokszor rendkívül gazdaságos lehet, hogy a komplementer szerepekbe komplementer módon "bedolgozott" kötelezetségeket önként, békében elfogadják az érintettek, és nem érzik úgy, hogy hatalmi helyzetben, kényszer hatására kellene teljesíteniük a rájuk háruló kötelezettségeket. Tudom, furcsa, sokaknak elfogadhatatlan, mégis azt állítom, hogy sem a jogi pozíciók, sem a társadalmi szerepek nincsenek feltétlen összekötve a normativitás jelenségével. A gyakorlatban persze tényleg nem nagyon lehet elválasztani őket egymástól, fogalmilag azonban a kapcsolat nem szükségszerű köztük. A komplementer szerepek kialakulhatnak és fennmaradhatnak normatív támogatottság, tehát az elvárások megsértése esetén alkalmazott szankció hiányában is. Elképzelhető, hogy kizárólag az érdekviszonyokra támaszkodó szerepmegosztás alakuljon ki a felek között, és bár mindig sérülékeny lehet az ilyen kapcsolat, de attól még az érdek összetarthatja a résztvevőket.Norma
A norma jellemzői
A norma leírásához összetevőire kell bontanunk a fogalmat, hogy ezáltal láthatóvá váljék, milyen elemi adatok szükségesek ahhoz, hogy egyértelműen megadhassunk egy adott normát. Von Wright hat összetevőt tartott elkülönítendőnek [vonwr]- norma tartalma (content of norm)
- norma modalitása (character of norm)
- norma feltétele (condition of norm)
- norma alkalma (occasion of norm)
- norma autoritása (authority of norm)
- norma címzettje (subject of norm)
A norma tartalma
A normatartalom fogalma alatt azt a cselekvést kell értenünk, amire a normatív befolyásolási szándék irányul. Ebben a felfogásban a tartalom valamilyen cselekvés, nem más. Nem világállapot, nem folyamat, nem változás, nem puszta esemény. Cselekvés, mint például a dohányzás, az autóvezetés, a szobába belépés, a köszönés stb. Azt, hogy a cselekvést hogyan lehet leírni a világállapotok, az átmetek, valamint a cselekvésoperátorok segítségével, a könyv egy korábbi fejezetében bemutattam (☜) A normák leírásakor nincs szükség többre, mint, hogy az ott bemutatottak szerint írjuk le a cselekvéseket, és ha így teszünk, egyúttal megadjuk a norma tartalmát is. Fontos figyelni arra, hogy a normatartalom megragadásakor nem vehetjük bele a norma deontikus értékét. A 'Ebben a helységben tilos a dohányzás!' norma esetében a norma tartalma "csak" a dohányzás lesz, a tiltás modalitását a norma másik összetevőjével írjuk le.A norma modalitása
Amit von Wright a norma karaktereként (character of norm) ad meg, azt én a norma modalitásaként nevezem. Modalitáson pedig azt a deontikus operátorral kifejezhető normatív szándékot ragadhatjuk meg, amellyel a normát kibocsátó (ellenőrző, számonkérő) személy a norma címzettjét cselekvésre akarja bírni. A deontikus modalitás kérdését alaposan elemeztem a könyvben, bővebb áttekintésekért ezekre a fejezetekre hivatkozom (☜) illetve (☜)A norma feltétele
Amilyen fontos fogalom a norma felétele, annyira könnyű félreértelmezni a jelentését. A 'feltételesség' sokjelentésű fogalma miatt könnyen zavar alakulhat ki. A norma feltételének – legalábbis a von wright-i interpretáció szerint – nincs köze a norma körülményeihez, ennek ellenére könnyű "összekeverni" őket a két fogalomban "megbúvó" feltételesség mozzanata miatt. Von Wright szerint minden normának van valamilyen alkalmazási feltétele (condition of application), ami lényege szerint a norma tartalmától függ. A sokszor idézett példa szerint ha egy normál ajtóval szemben állunk, akkor kiadhatják nekünk azt a parancsot, hogy 'Csukd be az ajtót!', de ennek az a feltétele, hogy (i) az ajtó nyitva legyen, és (ii) ne csukódjon be magától. Ellenben ha egy magától bezáródó ajtóról van szó, akkor értelmetlen kiadni az előző parancsot, hiszen az világban végbemenő állapotváltozás eredményeként becsukódik az magától. Egy ilyen világállapotban más parancsnak lehet csak értelme, például annak, hogy 'Ne engedd becsukódni az ajtót!'. Fontos hangsúlyozni, hogy minden normához tartozik a fenti értelemben vett alkalmazási feltétel, sőt, pontosabb lenne úgy fogalmazni, hogy tartoznia kell. De természetesen az alkalmazási feltételen kívül lehet még további feltételeket is a normákhoz rendelni, amelyek már nem szükségszerűen kapcsolódnak a normákhoz. Von Wright példája erre a 'Ha esik az eső, csukd be az ablakot!' felszólítás. Egy ilyen feltétel esetlegesen van a normához rendelve – szemben a norma alkalmazási feltételével. A kategorikus normák esetében az alkalmazási feltétel a norma cselekvéstartalma ismeretében is megállapíthatjuk, ezért mondja azt von Wright, hogy a kategorikus normák esetében elég az alkalmazási feltétel a tartalommal együtt adott [vonwr] ezért nincs szükség annak külön jelzésére a normát leíró logikai formalizmusban. Ezzel szemben a norma további feltételeit – ha vannak – meg kell tudnunk adni, ezért van szükség külön paraméter felvételére a normák összetevőkre bontása során. A hipotetikus normák feltételei tetszőlegesek lehetnek, elméletileg bármely világállapot lehet egy norma feltétele. A cselekvéselmélet számára azonban kiemelten fontosak azok a feltételek, amelyek egy másik cselekvésre, még pontosabban: egy másik ágens cselekvésére hivatkoznak (ilyen például a 'szemet szemért' parancs). Ezek a normák a reciprocitás és komplementaritás társadalmi helyzeteiben kiváltképp gyakoriak és fontosak.A norma alkalma
Vigyázni kell, hogy a norma alkalmazási körülményét, alkalmát (occasion of norm) ne keverjük össze a norma feltételével. Persze mondhatjuk azt, hogy a norma körülménye az a feltételrendszer, amely mellett a normát érvényesnek és követendőnek tartják az érintettek (vagy elgalább azok egy része), de ilyenkor is speciális feltételekre kell gondolnunk. A dolgokat kicsit leegyszerűsítve mondhatjuk, hogy a norma tér-idő meghatározottságáról van itt szó. A körülmény azért is fontos összetevő, mert a fogalmi terjedelmébe tartozó adatok alapján tudjuk tipizálni a normákat a partikularitás/univerzalitás dimenziója mentén (legalábbis részben).A norma autoritása
A norma mint a jövőbeni cselekvésekre vonatkozó szándékkinyilvánítás logikailag megköveteli, hogy legyen egy olyan ágens, aki a normát kibocsátja. Ezt a társadalmi szereplőt nevezzük a norma autoritásának. Vannak normák, amelyek esetében könnyen és egyértelműen meghatározhatjuk a norma kibocsátóját, de előfordulhatnak olyan esetek is, amikor igencsak nehéz megmondani, ki volt az adott norma autoritása. Az erkölcsi parancsok, a szokáserkölcs előírásai szinte mind ilyenek: a kibocsátójuk személye a történelem homályába vész. Részben a norma autoritása alapján válik lehetővé, hogy az autonómia kérdését meg tudjuk fogalmilag ragadni, és így egy újabb normatipogizálási lehetőséghez jussunk.A norma címzettje
A norma címzettje (subject of norm) az az ágens, akire vonatkozik a normában megtestesülő cselekvésbefolyásolási szándék, akinek a normában előírt cselekvástartalomhoz a norma modalitásértéke szerint kell (vagy lehet) viszonyulnia. Von Wright másfajta megfogalmazásában: a címzett hajtja végre azt a cselekvést, amelyre vonatkozóan az autoritás toleráns vagy intoleráns viszonyt nyilvánít ki. A címzett lehet partikuláris, egyedi (particular), illetve univerzális, általános (general). Ez a megkülönböztetés később – részben – alapul szolgálhat a normák egyfajta tipizálásához.A normasértés szankciója
Von Wright, bár megemlítette, mint fontos, a normához kapcsolható jelenséget, de nem vette fel külön a szankcionálás jelenségét, a társadalmi szankció fogalmát a norma összetevői közé. Mégha el is fogadom, hogy a szankcióra nem a norma összetevőjeként kell tekinteni, ez nem jelenti, nem jelentheti azt, hogy ne kellene mindenképpen beemelnünk a fogalmat a norma modelljébe. Szankció hiányában nem beszélhetünk normáról, ezért szükség van rá a norma jellemzőinek tárgyalásakor. Amikor von Wright a normák főbb típusait mutatta be, akkor normaként értelmezte a technikai normákat is, de én ezt az interpretációt nem fogadom el. Azon az alapon, hogy a technikai normák, a főzési receptek, a kezelési, szerelési útmutatók (például az IKEA-bútorok összeszerelését támogató vizuális segédletek), a használati leírások, szoftverkezelési kézikönyvek jelenségében nincs ott a társadalmi szankció mozzanata, ezért nem nevezhetjük ezeket társadalmi normának. Ezt Émile Durkheimhez is így gondolta, ahogy az kiderül a következő idézetből:"Ha ügyeimet nem a mesterség szabályainak megfelelően viszem, azt kockáztatom, hogy nem érek el sikert; de a társadalom nem emel szót az ellen, hogy így cselekedjek. Hagyja, hogy cselekvésem teljesen szabadon végbemenjen. Ez a cselekvés nem juthat el azokhoz a célokhoz, amelyek felé törekszik, de ezért még nem tiltatik meg." (Durkheim, idézi: [nemed]
Hiába van egyfajta "előírás", valamiféle mesterségbeli útmutató (technikai norma), és hiába nem követem az abban leírtakat, nem lesz rá társadalmi reakció. Ez nem jelenti azt, hogy ne lesz semmi következménye az útmutatótól való eltérésnek. Lehet, hiszen a technikai norma követése által remélt célt esetleg így nem érem el. De az eltérést ilyen esetekben nem követi szankció. Ha nem a recept szerint főzök, akkor ehetetlen lesz az étel, és ez következményként lehet igen kellemetlen, de társadalmi szankcióra nem kell számítanom. Nagyon fontos tehát, hogy a technikai előírások megsértéséből származó következményeket ne azonosítsuk, ne keverjük össze azzal, amikor a normasértést társadalmi szankció követi."Ha megsértem a higiénia szabályait, amelyek azt parancsolják nekem, hogy tartózkodjam a gyanús érintkezésektől, e cselekedetet automatikusan követi a káros következmény, … a betegség. Az elkövetett cselekmény magától váltja ki a következményt." [durkh]
Ezzel szemben a normasértés mindig valamilyen társadalmi helytelenítéssel találkozik, és a társadalom (közösség) vagy igyekszik megakadályozni a normasértőnek ígérkező cselekvést, vagy – ha ez már nem sikerült, akkor – valamilyen szankcióval sújtja a normától való eltérést."Ha egy cselekvés, amelynek természeténél fogva egy morális szabályhoz kell alkalmazkodnia, attól eltér, a társadalom, ha erről tájékoztatva van, közbelép, hogy megakadályozza ezt az eltérést. … Ez a társadalmi reakció igazi szükségszerűséggel követi a normasértést; gyakran még módjában is előre meghatározott." (Durkheimet idézi: [nemed]
A normasértés helytelenítése és szankcionálása elválaszthatatlan a norma jelenségétől, de persze mindkét jellemzőt (a helytelenítést, illetve a szankcionálást) megfelelő módon kell értelmeznünk. Nem követelhetjük meg azt, hogy akár a helytelenítés, akár a szankcionálás konszenzuális legyen, vagyis mindenki egyetértsen, illetve részt vegyen ezekben. Azt sem állíthatjuk, hogy minden normasértést szankció követne, sőt, ki kell mondanunk egy fontos tételt: amilyen mértékben előzetesen várható a szankcionálás tényleges bekövetkezése, olyan mértékben fognak az emberek igazodni a normákba foglalt előírásokhoz. Az is fontos kérdés, hogy a szankcionálásnak milyen eszközei, lehetőségei vannak, de ezt a normák tipizálásakor fogom megválaszolni (és a típusokat bemutatni).A norma érvényessége
A norma érvényessége alatt legitim érvényességet értek. Ezt a kérdéskörét az uralomról szóló fejezetben tárgyalom (☜)A normához való igazodás
A normavezérelt magatartásnak két fő típusa van: a normasértő vagy a normához igazodó cselekvés. A normasértésről már szóltam, most a normakonform magatartás jellemzésén van a sor. Előtte azonban tisztáznom kell valamit. A normához való igazodás nem feltétlen vonzza maga után a normakövető magatartást. Mind elméletileg, mind gyakorlatilag lényegi és szoros kapcsolatot tételezhetünk a normakövetés és a normához való igazodás között, de ez nem jelent kizárólagosságot. Csontos László a következő tényezőket sorolja fel a normakövetés magyarázata során."A normakövető egyéni cselekvés magyarázata során - durván - négy lehetséges mechanizmusra hivatkozhatunk: (1) a normától eltérő vagy normasértő (deviáns) viselkedés szankcionálása; (2) az egyéni stratégiaválasztástól függő nyeremények pozitiv interdependenciája (a normakövető magatartás – pozitív – externális hatása); (3) az egyéni preferenciákba épített konformizmus; és végül (4) ex ante kommunikáció az ex post normakövető csoport tagjai között." [Csont]
A pontosabb értelmezés érdekében bemutatok egy hétköznapi példát arra vonatkozóan, hogy milyen cselekvési stratégiákat lehet követni a nagyvárosi tömegközlekedési eszközök igénybevétele során. Az alapnorma úgy szól, hogy minden használatért fizetni kell (bérlet- vagy jegyvásárlással), a normasértés esetén pedig büntetést kell fizetni. Ebben a helyzetben az alábbi stratégiákra könnyedén találhatnánk valós példákat az utazóközönség tagjai közt.- 1.)] valaki havi bérletet vált;
- 2.)] valaki minden utazási alkalommal előre jegyet vesz és érvényesíti;
- 3.)] valaki minden utazási alkalommal előre jegyet vesz, de csak akkor érvényesíti, ha ellenőrökkel találkozik;
- 4.)] valaki nem vesz sem jegyet, sem bérletet, de ha a járművön találkozik a kalauzzal, tőle vesz jegyet (ilyen rendszer működik a Szentendrei HÉV-en);
- 5.)] valaki nem vesz sem jegyet, sem bérletet, ha ellenőrök elkapják, büntetést fizet.
"A kollektív érzelmek ugyanis, amelyeket a történelem adott időszakában egy nép büntetőjoga védelmez, csak akkor hatolhatnak be azokba az emlékekbe, amelyek eladdig zárva voltak előttük, s csak akkor tehetnek szert akkora hatalomra, amellyel addig nem rendelkeztek, ha a korábbinál nagyobb lesz az intenzitásuk. Az egész közösségnek erősebben kell éreznie ezeket az érzelmeket. Csakis innen meríthetnek ugyanis ezek az érzelmek olyan, a korábbinál nagyobb erőt, amelynek révén rákényszeríthetik magukat azokra az egyénekre is, akik ezt megelőzően leginkább ellenük szegültek. A gyilkosok csak akkor tűnhetnek el, ha a vérontástól valő irtózás a korábbinál jóval erősebbé válik azokban a társadalmi rétegekben is, ahonnét a gyilkosok rendszerint kikerülnek." [Emile]
Rögtön ezek után persze Durkheim hozzáteszi azt is, hogy a kollektív érzelmek megerősödése, amely – jó esetben – valamely bűntípus visszaszorulását, esetleg eltűnését eredményezi, "hozzájárul" ahhoz, hogy más területeken újfajta bűncselekmények "jelenjenek meg". Durkheim persze ennek is megadja a magyarázatát." … a közös tudat ilyen intenzív állapotai nem erősödhetnek meg anélkül, hogy ne erősítenék fel azokat a gyengébb állapotokat, amelyek áthágása addig csupán erkölcsi vétségnek számított. … [a kollektív] tudat sokkal érzékenyebben reagál majd azokra a sérelmekre, amelyek korábban alig érintették: erőteljesebben lép fel ellenük, jobban elítéli őket, s némelyiküket egyszerű erkölcsi fogyatékosságból bűncselekménnyé változtatja." [Emile]
Ezen a ponton kiváltképp "tetten érhető" a normavezérelt magatartás mélyén kitapintható, elemi erővel hatni képes értékalapja, érzelmi töltete. Eddig arra mutattam példát, hogy a normakövetés és normához való igazodás nem feltétlen esik egybe. Arra is figyelnünk érdemes azonban, hogy nem minden normális, nem minden szabályszerűnek tűnő cselekvést magyarázhatunk valamilyen mögöttes normához való igazodással. Rorbert B. Cialdini és szerzőtársai megkülönböztetnek kétféle kategóriát, a leíró norma (descriptive norm) és rendelkező norma (injunctive norm) fogalmát [Ciald] A leíró norma fogalma alatt ők elsősorban arra gondolnak, hogy ha valamilyen mintát sokan követnek, azt mindenkinek érdemes lesz követni, ezért az normává válik. Az én értelmezésemben Cialdiniék leíró normája nem igazán norma, hiszen nincs mögötte szankcionáló erő. Ezt nevezhetjüük hálózati hatásnak, közös tudásnak, szabályszerűségnek, de normának nem. Szankció nélkül nincs norma.A norma másodrendű kontextusa
A von wright-i normaösszetevők kiegészítését akkor érthetjük meg igazán, ha látjuk (és a modellünkben feltüntetjük), hogy a normavezérelt cselekvések sosem magukban állnak, így nem is értelmezhetők magukban. Az elemzés központjába természetesen a normavezérelt cselekvést kell helyeznünk, de emellett figyelembe kell vennünk még két másik cselekvéstípust is. A normavezérelt cselekvést a norma címzettje hajtja végre. Ennek során vagy igazodik a normába foglalt szándékhoz vagy megsérti a normatív elvárást. A normához való igazodáshoz azonban meg kell előzze az a cselekvés, amelynek során a normát magát kibocsátja valaki (ideértve a norma módosítását is). [♦] Ha viszont azt a szempontot is figyelembe vesszük, hogy a normákat nemcsak kibocsátani lehet, de megszüntetni vagy visszavonni is, akkor szükség van egy olyan általánosabb fogalomra, amely mind a kibocsátás, mind a visszavonás aktusát magába foglalja. Erre alkalmas lehet a deklarálás fogalma. A deklarálás tevékenységét az autoritáshoz köthetjük, és fontos kényszerként rögzíthetjük, hogy ennek a cselekvésnek időben meg kell előznie a normavezérelt cselekvést magát. Mivel pedig a norma deklarálása olyan cselekvés, amely más cselekvést magukba foglaló normákra vonatkozik, így logikai minőségét tekintve a deklarálást másodrendű cselekvésfogalomnak kell tekintenünk. A normavezérelt cselekvéshez tartozik még a szankcionálás aktusa is, ami a cselekvést követően, tehát ahhoz képest időben később valósul meg, de fogalmilag ugyanúgy elválaszthatatlanul kapcsolódik hozzá, mint a a kibocsátás cselekvése. A szankcionálás is másodrendű, hiszen mindig csak valamilyen elsőrendű (alacsonyabbrendű) cselekvésre hivatkozva értelmezhető, önmagában vett szankcióról sosem beszélhetünk. A szankció lehet pozitív, valamilyen jutalom, illetve negatív, valamilyen büntetés. A szankcionálást az autoritás végzi el, de fontos látni, hogy az autoritás szerepfogalom, és nem feltétlen egyezik meg az a két ágens, amely egy adott normával kapcsolatos kibocsátó, illetve szankcionáló szerepeket viszi. A normavezérelt cselekvés másodrendű kontextusán a fent bemutatott másodrendű cselekvéseket értem. A normatív jelenségek értelmezéséhez a norma összetevői mellé fel kell venni ezeket a jelemzőket is.
A norma összetevőinek bemutatása után belevághatunk a norma típusainak tárgyalásába. Ezt többszörös tipizálást lényegleg a normaösszetevőkre támaszkodva végzem majd el.
Normatípusok
A norma összetevői és egyéb jellemzői alapján már módunk nyílik arra, hogy a normákat különböző szempontok szerint tipologizáljuk. Bemutatom, hogy majdnem az összes normakompenens szerint lehet értelmesen normatípusokat képezni, de előfordul majd olyan felosztás is, amelyben egyszerre több összetevőt figyelembe véve lehet majd alábontani a norma fogalmát.Normatípusok a szankció típusa szerint
A normavezérelt cselekvés következménye valamilyen joghatás lesz. Joghatás alatt érthetjük a szankció bekövetkeztét is, nem részletezve azt, mit is érünk szankció alatt. Még azt is mondhatnánk, hogy a szankció lehet pozitív vagy negatív, tehát beszélhetünk jutalomról és büntetésről. A tényleges társadalmi gyakorlatok ismeretében azonban nem tévedünk nagyot, ha a szankció fogalma alatt itt csak a büntetést értjük, és a talán legfontosabb három normatípust a rájuk jellemző szankciók különbsége alapján határozzuk meg. Ezt a hármas tipológiát Max Webertől vehetjük át, akitől most egy kicsit hosszabban idézek:
"6.§. Valamely rend legitimitása biztosítható:
I. tisztán belülről, mégpedig
1. tisztán indulati-érzelmi alapon: érzelmi átéléssel, belső odaadással;
2. értékracionálisan: a végső és kötelező értékek (erkölcsi, esztétikai vagy bármely más értékek) kifejeződéseként fölfogott rend abszolút érvényességébe vetett hittel;
3. vallásos hittel: azzal a meggyőződéssel, hogy a rend betartásán keresztül el lehet jutni az üdvözüléshez;
II. továbbá úgy is (vagy csak úgy), hogy sajátos külső következményekhez kapcsolódnak bizonyos várakozások.
A rendet
a) konvenciónak nevezzük, ha érvényessége külsődlegesen, azáltal van biztosítva, hogy az emberek megadható körén belül a rendtől való eltérés várhatóan (viszonylag) általános és gyakorlatilag érezhető helytelenítésbe ütközik;
b) jognak nevezzük, ha ugyancsak külsődlegesen, de azáltal van biztosítva, hogy az emberek egy külön erre fölkészült csoportja várhatóan (fizikai vagy pszichikai) kényszert alkalmaz a rend betartásának kikényszerítésére, illetve megszegésének megtorlására."
[weber]
- erkölcs (belső szankció: az egyén lelkiismeret-furdalása)
- konvenció (külső szankció: a közösség helytelenítése, kritikája)
- jog (külső szankció: az erőszak-alkalmazással való fenyegetés)
"A » kívülről« biztosított rendnek azért még » belső« garanciái lehetnek. A szociológia számára nem probléma a jog, a konvenció és az » etika« kapcsolata. Az » etikai« mérce itt azt jelenti, hogy az emberek bizonyos speciális értékracionális hite normaként szolgál az olyan emberi cselekvés számára, amely az » erkölcsi jó« predikátumára tart igényt." [weber]
Ebben a gondolatmenetben már egy szinten, egyenrangúan (és kizárólagos módon) szerepel a rend három típusa, a jog, a konvenció és az etika, csak az nincs megfogalmazva, hogy az etikához (erkölcshöz) kapcsolható speciális szankció a lelkiismeretfurdalás. Amikor az alapvető cselekvéstípusok bemutatás végén felrajzoltam egy ábrát (☜) amivel az alapbeálítódások (cél- és értékracionalitás, indulat, habitualitás) egymáshoz való viszonyát próbáltam érzékeltetni, akkor a normavezérelt cselekvést úgy jelöltem, mint ami egyszerre "támaszkodik" az indulati-érzelmi, illetve az értékracionális cselekvéstípusokat jellemző beállítódásra, belső mechanizmusokra. A normák itt megadott – a szankcionálási mechanizmus különbségeire épített – hármas felosztása során már bővebben értelmeztem a norma fogalmát a korábbiakhoz képest. Amikor a társadalmi cselekvések típusait elemeztem, akkor még csak a másoktól független egyénre, egyéni cselekvésre figyeltem. Az egyes cselekvéstípusok elkülönítésekor is csak a belső motivációkra, belső hatásokra támaszkodnak. Most viszont már a külső befolyásolás lehetőségét is figyelembe vettem a normák tipizálása során. A konvenció és a jog fogalmaival már olyan normativitást ragadhatunk meg, amelyben a normához való igazodást külső szankciók figyelembe vételével magyarázhatjuk meg. Mit is jelent ez a cselekvéstípusokra nézve? Azt, hogy ezek a "sajátos külső következményekhez kapcsolódó várakozások" racionális, mérlegelő magatartáson keresztül érvényesülnek. Vagyis amilyen mértékben beszélhetünk a konvencióhoz vagy joghoz igazodó cselekvésről, olyan mértékben válik meghatározóvá a racionális beállítódás, vagyis a racionális megfontolásokkal magyarázható normakövetés. Természetesen mindig elképzelhető, hogy valakiben mindhárom szankcionálási mechanizmus egyszerre van jelen, amikoris azt mondhatjuk, hogy az illető voltaképpen mindhárom normatípushoz igazodik a cselekvésében (vagyis egyszerre erkölcsi, jogkövető vagy konvencionális cselekvést hajt végre). De az is könnyen elképzelhető, hogy egy normához igazodó cselekvést csak hideg mérlegelés alapján hajt végre, és semmi belső motiváció nincs benne a norma követése iránt (például az élvezetből gyorshajtó ember csak akkor tartja be a sebességkorlátokat, amikor komoly esélyét látja a lebukásnak – ez a színtiszta racionális alapon álló normakövetés példája).Normatípusok a logikai rend szerint
A norma tartalma és szankciója alapján elsőrendű vagy magasabbrendű normákat különíthetünk el egymástól. Elméletileg tetszőlegesen magas rendű normát el lehet képzelni, de a gyakorlatban vélhetőleg harmadrendű normáknál nem nagyon találunk magasabbrendűeket. A szakirodalomban az első- és másodrendű normákkal sokat foglalkoznak, harmadrendűekkel már jóval kevesebbet, és arról nem tudok, hogy a harmadrend fölött bármilyen elemzés született volna. Pedig azt gyanítom, hogy egy alaposabb elemzés kideríthetné, hogy – főleg, mióta az európai uniós jogkörnyezetbe kerültünk – előfordulnak negyed-, netán ötödrendű normák tényleges joggyakorlatban, csak ez – már, ha tényleg létezik – azért nem okoz gondot, mert az adott kontextusban, a tényleges jogi környezetben "közelről" nem lehet érzékelni a magasabb rendbe való kerülést. De nem is az az igazán fontos kérdés, hogy milyen másodrendnél magasabb normák vannak (egyáltalán vannak-e), hanem sokkal inkább azt kell látnunk, hogy hol, milyen másodrendű normákat találhatunk. Von Wright a normáról szóló könyve egyik fejezetét a magasabbrendű normáknak szenteli [vonwr] Itt vezeti be a kompetencianorma fogalmát, amire már utaltam a hohfeldi elmélet elemzésekor (☜) A fogalom definíciójából következik, hogy a kompetencianormát (a hohfeldi felhatalmazottságot) delegáló normáknak is tekinthetjük, ami egyfajta normahierarchia kialakítására és kezelésére lehet alkalmas. Jog esetében az állam az alárendelt hatóságok számára átengedhet felhatalmazottságot, hogy így a közjót jobban ki tudja szolgálni."Előfordul, hogy a legfelsőbb hatóság bizonyos dolgokat szabályozni akar, mondjuk úgy, a közjó érdekében. Ilyenkor a jogszabályi részletek kidolgozását olyan alacsonyabb szintű hatóságra hagyhatja, amely megfelelő ismeretekkel rendelkezik a cél, az adott közjó megvalósításához szükséges speciális követelményekről." [vonwr]
Persze, von Wright nem volt se jogász, se szociológus, se antropológus, így a társadalmi cselekvések elemzésével kapcsolatban nem tudott, nem is akart továbblépni. A magasabbrendű normatív fogalmakat a jogviszonyok, jogrendszer elemzése kapcsán először jogászok bontották ki alaposabban. Már Hans Kelsen is beszélt első- és másodrendű jogszabályokról, de ő nem logikai értelmezés szerint sorolta ilyen típusokba a jogszabályokat, hanem a jogrendszer működési logikája szerinti fontosságot tekintette meghatározónak [kelse] Ezért ő a logikai interpretációhoz képest pont fordítva minősítette a jogszabályokat, és a bírókat az ítélkezési folyamat során kötelező szabályokat nevezte elsőrendűnek, míg az egyszerű állampolgároknak, a jog alanyainak tetszőleges, mindennapi tevékenységét szabályozó normákat tekintette másodrendűeknek. Ez a megközelítés pont az ellentéte a logikai-fogalmi gondolkodásnak. Természetesen itt csak eltérő terminológiai választásról van szó, fogalmi hibáról nem beszélhetünk. Amikor H.L.A. Hart elsődleges és másodlagos szabályokról írt, akkor ő már a szokásos logikai interpretációnak megfelelő szemléletben osztotta fel a jogszabályokat [hart:] A három híres másodrendű szabálya közül az elismerési szabály abban az értelemben különbözik a másik kettőtől, az ítélkezési és a változtatási szabályoktól, hogy az előbbi a jog egészének érvényességével kapcsolatos, míg az utóbbi kettő a jogrendszer fontos szereplőinek tevékenységére vonatkozik. A bírónak, rendőrnek másodrendű kötelessége van a szankciókat kiosztani a normasértések esetén, az ítélkezési szabályok a rájuk vonatkozó jogviszonyokat szabályozzák. A törvényhozónak, a jogalkotónak magasabbrendű joga (felhatalmazottsága) van az elsőrendű (olykor a másodrendű) jogviszonyokat megváltoztatni. A felhatalmazottságról szóló fejezetben már jeleztem, hogy a jog elemzése során kialakított jogviszonyfogalmak, az azokkal kapcsolatos tanulságok általánosíthatók és kiterjeszthetők az általánosabb normafogalmakra is. A legkülönfélébb társadalmi intézményekben, a családban, a munkahelyeken, az iskolákban, a társadalmi, kulturális, politikai szervezetekben mindenhol találhatunk elsőrendű szabályokat, normákat, amelyek a résztvevők mindennapi cselekvéseit szabályozzák, és vannak másodrendű normák, szabályok, amelyek az éppen aktuális normarend megváltoztatásának módját határozzák meg. Ezek lehetnek konvenciók, lehetnek szervezeti szabályzatok mint gyenge jogszabályok, de lehetnek akár morális szabályok is. A másodrendű szabályoknak pedig minden esetben, minden területen ugyanazok a funkciói, mint amit már a jog esetében korábban megismertünk: elismerni (eredeztetni), változatni, ítélkezni (fenntartani). Azt jeleztem ugyan, hogy léteznek a másodrendű szabályoknál magasabbrendűek is, de eddig igazából csak a másodrendű normákról beszéltem. Bár a másodrendű szint alapvető fontosságát (elsődlegességét) nem akarom kétségbe vonni, szükségesnek tartom jelezni, hogy minden normatív rendszerben vannak, kellenek, hogy legyenek harmadrendű szabályok. Ezért bemutatok egy egyszerű, hétköznapi példát a harmadrendű norma létezésére, működésére. Egy családnál gyerekzsúrt tartanak, és a kisgyerekeket egyedül hagyják egész délután a nagyszobában játszani. Este, miután minden vendég elment, az anyuka észreveszi, hogy a csokitorta egy részét valaki belepaskolta a drága perzsaszőnyegbe. Amikor kérdőre vonja ezért a kisfiát, a gyerek azzal vág vissza, hogy nem ő volt, aki ezt csinálta, hanem Zsoltika. Az első megszólalásával az anyuka másodrendű cselekvést hajt végre, hiszen elsőre szóbeli feddésben részesíti vagyis szankcionálja a fiát. Amikor azonban kiderül, hogy az elsőrendű cselekvés szintjén nem a fia volt a rendetlen (a normasértő), akkor az anyuka visszakérdez: 'Miért nem szóltál rá Zsoltikára, hogy nem szabad ilyet csinálni?' Ez a feddő kérdés már harmadrendű cselekvésnek számít, hiszen az anya feddése annak a mulasztásnak szól, hogy a fia nem szankcionálta (másodrendű cselekvés) a vendégét, aki rosszalkodott (elsőrendű cselekvés).Normatípusok a deontikus modalitás szerint
A norma modalitása alapján is adott egy természetes tipizálási lehetősége, hiszen a deontikus logikai kategóriák alapján a normákat élesen elkülöníthetjük egymástól. Attól függően, hogy milyen deontikus logikai operátorokat veszünk fel a deontikus logikai modellünkbe, beszélhetünk három, négy vagy hat modalitás szerinti normatípusról (úgymint: kötelező, megengedő, tiltó, mellőzhető, opcionális vagy preskriptív normákról). Ahhoz képest, hogy eldöntjük, hányféle deontikus modalitással akarjuk kezelni a normatív teret, illetve melyek ezek, az már egy másik kérdés, hogy ezeket a deontikus operátorokat fogalmilag, logikailag hogyan írjuk le, és egy formális ontológiába miket hogyan veszünk fel a természetes nyelvi szinten használt kifejezésekből. Von Wright a kötelezést és a tiltást egymásból levezethetőnek tartja, ezért elegendőnek tartja csak az egyiket felvenni a modelljébe [vonwr] Ezt a kötelező normával (O, O-norm) teszi meg. A megengedés aktusát viszont – jelezve annak vitatott státusát – önállóan kezelendőnek ítéli, és ezért külön felveszi saját ontológiájába a permisszív normát (P, P-norm). Mások szerint a logikai szinten elegendő egyetlen deontikus operátor, és minden más egyéb levezethető belőle (bővebben erről (☜) A normák deontikus modalitás szerinti tipizálásában érdemes Hohfeld elméletét, fogalmait is figyelembe venni. Bár a hohfeldi másodrendű jogfogalmak deontikus logikai minőségüket nem jelentenek új típusokat, gyakorlati jelentőségük miatt érdemes felvenni őket a normák deontikus modalitás szerinti osztályozása során. Eközben persze azt is figyelembe kell venünk, hogy a két másodrendű hohfeldi fogalmat, a felhatalmazottságot és a mentességet nemcsak itt használhatjuk önálló altípusként, de a normák logikai rend szerint csoportosításakor is. A klasszifikációhoz ugyan nem járul hozzá a Hohfeld által megállapított jogok és kötelezettségek közti komplementaritás figyelembe vétele, hiszen a hohfeldi korrelativitás csak a normatípus közti viszonyokat ragadja meg, nem ad új alosztályt. De a korrelatív kapcsolatban levő normaviszonyok mégiscsak a deontikus modalitás szerinti normatípusokat kapcsolják össze egymással, így a korrelativitás "követése" révén további tudást lehetséges a normatív viszonyokNormatípusok a tartalom szerint
A logikai elemzésekben nemigen találhatunk olyan kísérleteket, amelyek a norma tartalma alapján tipizálná a normákat. Vélhetőleg azért nem, mert az ilyen vizsgálat kivezet a logika területéről. Ebből a szempontból tekintve nyilván sokféle tipizálás elképzelhető. A legtermékenyebbnek a játékelmélet játékosztályai szerint elvégezhető tipizálási lehetőségeket érzem, amit nagy vonalakban be is mutattam a játékelméleti fejezetben (☜) Robinson és Goforth mind a 144 kétszemélyes alapjátékot nagyobb játékosztályokba sorolta azok "geometriai jellemzői" alapján [Robin] Ugyancsak játékelméleti alapokon állva Edna Ullmann-Margalit az alapjátszmákat három nagy osztályba sorolva be elkülönítette a koordinációs normákat (coordination norms), a fogolydilemma normákat (Prisoners' Dilemma norms) és a részrehajló normákat (inequality or partiality norms) egymástól [ullma] A dawid lewisi konvencióértelmezés [david] nyomán kialakuló diskurzusban a koordinációs problémák két fő osztályát a tiszta koordinációs és az antikoordinációs helyzeteket feloldó konvenciók mentén lehet egyfajta normatipizálást elvégezni. Robert Sugden három konveciótpípust határolt el, amikor elkülönítette egymástól a koordinációs helyzetekkel, a tulajdonnal, valamint a reciprocitással kapcsolatos konvenciókat [sugde] A normák egyik fontos tartalmi altípusának kell tekintenünk a méltányossági normákat, melyek kialakulásáról Ken Binmore cikke ad érdekes áttekintést [Binmo]Normatípusok az érvényesség alapján
A normákat – a jogi normákat biztosan, de a konvencionális és morális normákat is, mégha kicsit nehezebben – tipizálhatjuk az érvényesség, pontosabban a hatályba lépés szempontja szerint. Egy norma lehet hatályos, illetve hatályon kívüli. Hatályos norma esetén az autoritás (a kibocsátói vagy a szankcionáló szerepben) a legitim érvényességre hivatkozva igényli a normához való igazodást a címzettektől, míg a hatályon kívüli norma esetében nincs ilyen igény.Normatípusok az autoritás alapján
Fogalmilag már kivezet a módszertani individualizmus világából, ha az autoritástípusok alapján próbáljuk meg tipizálni a normákat, ám a komoly szociológiai relevanciája miatt mindenképpen be kell mutatnom ezt a klasszifikációs sémát. Ha a széles értelemben vett jogra gondolunk, arra a tételes normarendre, amit emberek hoznak saját életük szabályozására ideértve mind az egységes és centralizált állami jogrendszer, mind az osztottabb, korlátozottabb hatókörű, ám nagyobb számosságú szervezeti világ működési szabályait, akkor a normák kibocsátói szerint elkülöníthetjük az alábbi normatípusokat: törvény, rendelet, ítélet, szabályzat. Az elkülönítés alapja az, hogy milyen típusú szerv a norma kibocsátója. Ha a törvényhoző szerv, akkor a norma törvény, ha államigazgatási hatóság, valamilyen végrehajtó szerv az autoritás:, akkor a norma rendelet, ha bírósági szerv az autoritás, akkor a norma bírósági ítélet, és ha az autoritás nem egy államigazgatási szerv, hanem valamilyen gazdasági, társadalmi, politikai, de államtól független szervezet, akkor a norma szervezeti és működési szabályzat.Normatípusok a címzett és autoritás viszonya alapján
A norma címzettje és autoritása az a két társadalmi szerep, amely mentén az ágenseket a normákhoz kapcsolhatjuk. E két szerep egymáshoz való viszonya alapján egy olyan felosztáshoz juthatunk, amely egy jól ismert és nagyon széles körben használt kettősséget eredményez, jelesül az autonóm (autonomous norm), illetve a heteronóm norma (heteronomous norm) dichotómiáját [vonwr] Ha a norma kibocsátója, tehát az autoritás és a norma címzettje megegyezik egymással, akkor beszélhetünk autonómiáról, autonóm normáról, ellenkező esetben pedig a norma heteronóm. Ez a felosztás jól alkalmazható a jog, a racionális uralom világában, ahol sok helyen megtalálhatjuk mind az autonómia, mind a heteronómia jelenségét (ehhez presze a jogot általánosabb értelemben kell interpretálnunk, mint az állam által teremtett normatív rendszert). Nem ilyen egyértelmű a helyzet a konvenció és a morál területén, hiszen ilyen esetekben nem mindig lehet (vagy szinte sosem lehet) megmondani, hogy ki a norma kibocsátója. Sokszor nem is beszélhetünk kibocsátóról, kibocsátásról. Von Wright ezt pont ellentétesen látja. Szerinte a morál lehet autonóm, a preskripció (durván: a jog) nem igazán. Ezt azon az alapon állítja, hogy a morálnak (és a konvenciónak, bár ezt ő nem említi) nem ismert a kibocsátója, és így az autonómia azt jelenti, hogy nem valaki mástól (nem egy konkrét ágenstől) származik a norma. Ezzel szemben von Wright nem tartja lehetségesnek, hogy valaki önmagának bocsásson ki egy normát, vagyis a preskripció szerinte nem lehet autonóm – legfeljebb csak valami másodlagos, analógiás, átvitt értelemben [vonwr] Ez a von wright-i ellenvetés hamar súlyát veszti, ha az egyéni cselekvők szintjéről egy kicsit elmozdulunk a kollektív cselekvések irányába. Mégha egyet is értenénk von Wright nézetével, a szervezetek világában már egészen biztosan értelmesnek, használhatónak kell gondolnunk az autonóm és heteronóm minősítéseket.Normatípusok a címzett és az alkalom szerint
A norma összetevői között a címzett, az alkalom és a feltétel az a három elem, amelyben egyedi, partikuláris dolgokat is kifejezhetünk. A másik három öszetevőben általános, generális információt adhatunk meg. A normák egyedi, partikuláris minőségét értelemszerűen csak az ennek kifejezésére képes összetevők segítségével ragadhatjuk meg, míg a normák általános, univerzális minőségének reprezentálására bármely normaösszetevőt használhatjuk. Mivel nem minden normához tartozik feltétel, ezért egy norma partikularitását annak címzettjén, illetve alkalmán keresztül jelezhetjük. Ezt teszi von Wright is, amikor a normákat a partikuláris-univerzális dimenzió mentén tipizálja [vonwr] Igazodva az általa javasolt terminológiához elkülöníthetjük a partikuláris, egyedi normákat (particular norm) és az univerzális, általános normákat (general norm) egymástól. Egy norma esetében mind a címzettre, mind az alkalomra teljesen egyedi, teljesen konkrét adatokat megadhatunk. Mondhatjuk azt, hogy egy vagy több konkrét emberre vonatkozik a norma, de egyedi tér-idő adatok megadásával megszabhatjuk a különös vagyis egyedi alkalmazási körülményeket is. Eszerint a norma címzettje és alkalma lehet partikuláris, egyedi, illetve generális, általános. Ezek alapján definiálhatunk új normatípusokat. Az egyedi normákhoz (particular norm) akkor jutunk, ha mind a norma címzettje, mind az alkalma partikuláris, egyedi. Ezzel szemben egy általános normát (general norm) úgy adhatunk meg, hogy vagy a címzett vagy az alkalom (vagy mindkettő) általános [vonwr] Ehhez hozzáteszi még von Wright azt is, hogyha mindkét összetevő általános, akkor a normát teljesen általánosnak (eminently general norm) lehet nevezni.Normatípusok a feltételesség alapján
A norma feltételének fogalma a normák természetes tipizálásra is módot ad [vonwr] Von Wright elkülöníti egymástól a kategorikus (categorical norm) és a hipotetikus normákat (hypothetical norm). Ezt azon az alapon teszi meg, hogy van-e a természetes alkalmazási feltételeken kívül további feltétel a normához rendelve. Ha nincs, akkor beszélhetünk kategorikus normákról, ha van, akkor hipotetikus normákról van szó. A kategorikus és hipotetikus norma bemutatásakor már jeleztem, nagyon vigyázni kell arra, hogy ne keverjük össze egymással (i) a norma kategorikus feltételeit, (ii) a hipotetikus norma "feltételességébe tartozó" feltételeket, valamint (iii) a norma alkalma, alkalmazási körülményei fogalma alá sorolható feltételeket. További nehézséget okozhat az a további körülmény, hogy (iv) a normához tartozó szankciót is kondicionális logikai kapcsolóval, azaz egy feltétellel kötjük össze a normasértés tényét rögzítő propozícióval. A 'feltétel' terminust tehát legalább négyféle értelemben alkalmazhatjuk, és ebben a helyzetben könnyen lehet tévedni. Jakab András a norma szerkezetének vizsgálatáról szóló tanulmányában azt nyilván helyesen állapítja meg [Jakab] hogy a tényállás és jogkövetkezmény között van egy kondicionális kapcsoló, amit lehet többféleképpen is ki lehet fejezni (és ezáltal kategorikus vagy hipotetikus formában reprezentálni), de a von wright-i értelemben vett hipotetikusság-kategorikusság csak a tényállásra, még pontosabban arra a diszpozícióra vonatkozik, amely a cselekvésre vonatkozó előírást tartalmazza. Jakab állításával ellentétben tehát továbbra van értelme hipotetikus normáról beszélni. A hipotetikusság értelmességére (és szükségességére) vonatkozóan bemutatok egy ismert példát, hogy rajta keresztül érzékeltethessem a hipotetikus és kategorikus normák közti különbséget. Vegyük az alábbi bibliai példamondatokat (normákat).
1.)
Ha megdobnak kővel, dobd vissza kenyérrel!
2.)
Szemet szemért, fogat fogért!
1'.)
Dobd meg kenyérrel!
2'.)
Szúrd ki a szemét, üsd ki a fogát!
A normatípusok áttekintése
A különböző tulajdonságok, összetevők mentén megalkotott normatípusokat egyetlen áttekintő ábrában bemutatva láthatóvá válik, hogy az egyes szempontok, dimenziók szerint milyen típusokat különíthetünk el egymástól. Ha pedig arra is gondolunk, hogy ezeket a különböző típusképző szempontokat egyszerre is érvényesíthetjük, tehát további altípusokat kaphatunk, akkor látszik, hogy egy igencsak kiterjedt, sokszempontú normatipológia áll rendelkezésünkre.
A normák tipizálási lehetőségeinek bemutatása után lehetne még a normák kialakulásának és fennmaradásának mechanizmusairól írni, de ezt a kérdéskört most nem tárgyalom (magyar nyelven ajánlom Orthmayr Imre áttekintését a társadalmi normák döntéselméleti és evolúciós magyarázatairól [orthm]
Uralom
Egyáltalán nem szokványos dolog az uralom és hatalom jelenségét egymástól elválasztva tárgyalni. Maga Weber is egymás mellett definiálta a két fogalmat, és a későbbi Weber-recepció egyszerre kezelte őket. Érdekes módon viszont sem Weber, sem követői nem törekedtek igazán arra, hogy megmondják, mi is a két fogalom közti különbség. Ezt a kérdést e fejezet végén próbálom majd a lehető legpontosabban megválaszolni, de addig is érdemes megindokolnom azt, hogy miért itt bontom ki az uralom fogalmát. Már csak azért is, mert az indokolásul felhozandó tételnek köze lesz a hatalom és uralom közti különbség magyarázatához is, és ennyiben megelőlegezi a később kifejtendő választ is. Az uralom fogalmának tárgyalását azért ágyaztam be a jogi viszonyokat és a normákat taglaló fejezetbe, mert a hatalomhoz képest az uralom sajátosságát az utóbbi normatív minősége biztosítja. Illetve még erősebbet lehet mondani: a norma és az uralom fogalma lényegében elválaszthatatlanok egymástól – nemcsak gyakorlati, de fogalmi értelemben is. [♦] Mielőtt ezt a tézist bővebben kifejteném és megvédeném, előtte tisztáznom kell még pár dolgot. Először idézzük fel, hogyan definiálta Weber az uralom fogalmát."Uralomról beszélünk, ha van rá esély, hogy egy meghatározott tartalmú parancsnak megadható személyek engedelmeskedni fognak… az » uralom« szociológiai szempontból csakis azt jelentheti, hogy egy parancs várhatóan engedelmességgel fog találkozni." [weber]
Fontos rögzítenünk, hogy itt elsődlegesen cselekvésbefolyásolásról beszélünk, aminek a központi mozzanata az egyén cselekvésére irányuló akarata. A cselekvésbefolyásolás lényege abban van, hogy valakinek a saját cselekvésére irányuló akarata megváltozik egy másik ember kinyilvánított akaratának hatására. Lehet valakit vitán keresztül befolyásolni, aminek eredményeként megváltoztatja a véleményét. Bármennyire is fontos ez a helyzet a társadalmi cselekvések világában, nem ezen a ponton helyénvaló foglalkozni vele. A véleménybefolyásolás kérdésköre lényegi módon áll távol az uralom (és hatalom) jelenségétől. A véleménybefolyásolásnak lehetnek különböző technikái, módjai, de abban mind közösek, hogy olyan hiedelemvilágot alakítanak ki a másik emberben, ami alapján azt gondolhatja magáról, hogy külső akarati befolyástól mentesen, szabad akarata szerint cselekszik. A hatalom és uralom szempontjából ez az opció érdektelen, legfőképpen azért, mert ilyenkor csak véleménybefolyásolásról, de nem cselekvésbefolyásolásról beszélhetünk. Ez utóbbi lényege (az előbbihez képest) abban van, hogy a cselekvésbefolyásolási szándék a másik ember cselekvését meghatározó akarat befolyásolására irányul. Valamely cselekvést lehet akarni vagy nem akarni, de valamilyen vélekedést nem lehet sem akarni, sem nem akarni, egy vélekedés vagy van, vagy nincs. Természetesen lehet arra törekedni, hogy valaki rendelkezzen valamilyen tudással, ebben az értelemben lehet akarni azt, hogy tudjon valaki valamit, de a tudást, vélekedést akarni nem lehet. [♦] Persze fel lehetne tenni a kérdést, hogy hol is látjuk, láthatjuk-e egyáltalán az akarat fogalmát magát a weberi definícióban. Nos, ott van a parancs fogalmában. Ha meg akarjuk határozni az akarat fogalmát, akkor több összetevőt kell egymás mellé helyezni. Weber egy helyütt kinyilvánított akaratként (manifasted will) hivatkozik rá [MaxWe] Ez fontos komponens, de önmagában még kevés. Hozzá kell tenni azt is, hogy ez a kinyilvánított akarat mások cselekvésére irányul. Önmagunknak nem adunk parancsokat, csak másoknak. Annyit tehát rögzíthetünk, hogy a parancs mások cselekvésére vonatkozó, kinyilvánított akarat. Ehhez azonban hozzá kell még tenni valamit, de azt csak később tudom indokolni, hogy mit és miért. A második észrevételem az uralom meghatározásával kapcsolatban az, hogy az uralom jelenségét egy pillanatig sem szabad úgy felfogni, mint aminek létezését, előfordulását a jog, a politika, az állam világára lehetne leszűkíteni. Az uralom ott van szinte minden társadalmi viszonyunkban, ott van minden társadalmi intézményben, a családban, a párkapcsolatban, az iskolában, a munkahelyen, társadalmi szervezetekben stb. Mivel már összekapcsoltam az uralom és a norma fogalmát, mondhatom, hogy az uralom minden normatív viszonyban megtalálható. És abból bizony "nagyon sok van". Harmadjára azt emelném ki a weberi definícióból, hogy ami parancsadás az egyik oldalról, az engedelmeskedés a másik oldalról nézve. Az uralom fogalmának talán legfontosabb összetevője a mindenféle érdektől független engedelmeskedni akarás mozzanata. A meghatározásban ugyan "csak" várható engedelmeskedésről beszél Weber, de a definícióhoz kapcsolt értelmező szövegrészben már lényegi elemként hangsúlyozza az engedelmeskedni akarás mozzanatát. Ezt azt jelenti, hogy az uralom önkéntes, a parancsnak a címzettek nem valamilyen kényszer hatására engedelmeskednek, hanem önszántukból, szabadon. Akik végrehajtják mások uralmi parancsait, azok valamilyen módon, valamilyen szinten akarják az engedelmeskedést magát. Ez az engedelmeskedni akarás jelenti, ez jelzi, ez konstituálja az uralom érvényességét, elfogadottságát. És ez adja a döntő különbséget a hatalommal szemben, ami mindig a kényszeren alapul. De erről majd később. Fe lehet, sőt fel is kell tenni a kérdést, hogy miért engedelmeskednek egyáltalán az emberek az uralmi kapcsolatokban. Erre megint csak később tudok pontosan válaszolni, de azt – a weberi meghatározás negyedik elemeként – már itt is rögzíthetem, hogy amikor az "alávetettek", vagyis a parancs végrehajtására felszólítottak valóban teljesítik a parancsot, akkor azt úgy kell értelmeznünk, hogy a kiadott parancsot az alávetettek elismerésre méltónak (példaszerűnek, mintaszerűnek), vagyis belsőleg érvényesnek tartják. Azt is mondhatjuk erre, hogy elismerik az uralmat magát. Meg azt, hogy az uralomban mindig van valami autoritás, valami tekintély. Ebből fakad az, amit Joseph Raz a jog preemtív jellegének nevez [Josep] de amit nyugodtan ráhúzhatunk minden uralmi jelenségre, hogy ti. minden uralmi (és tegyük most már hozzá: minden normatív) jelenségben ott van az a sajátosság ("képesség"), hogy a cselekvések gyakorlati indokainak keresése, mérlegelése során képes mindent kizárni, az érvelési teret teljesen kiüresíteni, oda egyedül sajátmagát belehelyezni, minden más gyakorlati indok helyébe lépni. Fel kell tárnom még egy további fontos mozzanatot az uralom jelenségéből, ami a weberi definícióban nincs ugyan explicite jelen, de az értelmező megjegyzések között már felbukkan, fogalmilag pedig nélkülözhetetlen. Ha belegondolunk egy egyszerű uralmi szituációba, akkor észrevehetjük, hogy a parancsot kiadó fél igénnyel lép fel a másikkal szemben, mégpedig engedelmeskedési igénnyel. Nem könnyű észrevenni, hogy a működő, már "beállt" uralmi viszonyok mennyire magától értetődően támaszkodnak erre az engedelmeskedési igényre, ami az uralmat gyakorló fél fejében lapul. Könnyen felfedezhetjük azonban ennek az összetevőnek a fontosságát (mi több, definitív módon szükségszerű létezését), ha elképzelünk egy kísérletet magunkkal. Ha azt a feladatot kapnánk, hogy "menjünk oda az utcán ismeretlenekhez, és mondjuk nekik azt, hogy meg kell írniuk a második zárthelyi dolgozatukat, vegyenek elő papírt, hogy lediktálhassuk a kérdéseket", akkor ezt a – tanárként egyébként havonta rutinosan elvégzett – műveletet képtelenek lennénk megcsinálni. A legfőbb indokunk pedig az lenne a végrehajtás ellen, hogy nem tudunk semmi érvet felhozni annak védelmében, hogy miért kéne az ismeretleneknek végrehajtaniuk a kiadott parancsainkat. Az engedelmeskedési igény hiányozna bennünk a leginkább (amit a tantermi szituációkban annyira természetesnek érezzük, hogy már észre sem vesszük). Tovább bonyolódik azonban a kép, ha felismerjük, hogy a résztvevők még egy másik és másfajta igényt is "kezelnek" ebben a helyzetben. Weber ezt legitimitásigénynek nevezi [weber] A legitimitásigény fogalmának értelmezéséhez H.L.A. Hart egy szembeállítását hívhatjuk segítségül. Hart a jog és a szokás fogalmát úgy állította egymással szembe, hogy a joghoz a belső szemlélet (internal aspect), míg a szokáshoz a külső szemlélet (external aspect) hozzárendelését javasolta."… ahhoz, hogy egy társadalmi szabály létezzen, legalább néhány embernek úgy kell tekintenie a kérdéses magatartást, mint a csoport egésze részéről követendő általános mintát. Egy társadalmi szabálynak létezik tehát egy » belső szemlélete« is, azon a külső szemléleten túl, melyben nem különbözik egy társadalmi szokástól, és ami nem más, mint az ismétlődő viselkedés, amit egy megfigyelő észlelhet." [hart:]
Ez a közös belső szemlélet az, ami képes összetartani – legalább bizonyos emberek számára – a normák, és ezen belül az uralmi normák vagy másként: az uralmi (engedelmeskedési) igények érvényességére vonatkozó hiteket. Az uralom lényegéhez tartozik a parancsot kiadók engedelmeskedési igénye egyfelől, illetve az alávetettek engedelmeskedni akarása másfelől, és ezekre irányuló belső hiteket valamilyen gyakorlati érvekkel meg kell tudni támogatni. Az (uralmi) normák érvényességére (legitimitására) vonatkozóan azonban nemcsak versengő hitek, de a hiteket megelőző, megalapozó versengő világszemléletek is vonatkoznak. Magára a normatív érvényességre, a legitimitásra többféle és – ami fontosabb – többfajta érvet lehet szolgáltatni. A legitimitásigények eltérésének szemléltetésére idézek egy politikai nyilatkozatot, amelyen belül egyértelműen tetten érhető az eltérő legitimitáshitek léte és konfliktusa."Az iráni kormány nem ismer el más tekintélyt vagy hatalmat, csak a Mindenható Istenét, és semmiféle jogi hagyományt, csak az iszlám törvényét. Ilyen feltételek mellett az iráni delegáció újra megerősíti, hogy a nemzetközi szervezetek iszlámmal ellentétes nyilatkozatainak, határozatainak vagy döntéseinek semmiféle érvényessége nincs az Iszlám Köztársaságban. Az » Emberi Jogok Egyetemes Nyilatkozata«, amely a zsidó-keresztény hagyomány világi koncepcióját illusztrálja, nem alkalmazható a muzulmánok által, és egyáltalán nem kapcsolódik az Iráni Iszlám Köztársaság által elismert értékrendhez; az Iráni Iszlám Köztársaság ezért nem habozhat e rendelkezések megsértésekor, ha az ország isteni törvényének megsértése vagy a világi egyezségokmányok megsértése között kell választania." [roula]
A fenti idézet önmagában elég ahhoz, hogy lássuk, miért is kell többféle legtimitásigényről (és legitimitástípusról) beszélni, illetve a konkrét példában az is szépen látszik, hogy ezek a különböző legitimitásigények, legitimitáshitek valóban versengő viszonyban vannak egymással. Összegzésként tehát azt kell rögzítenünk, hogy minden uralmi kapcsolatban kétféle igény, egy engedelmeskedési igény, illetve egy legitmitásigény bújik meg, és az uralom tényleges megvalósulásáról akkor beszélhetünk, ha ezt a két igényt az uralmat gyakorolni kívánók sikeresen el tudják fogadtatni az uralomnak alávetettekkel. A legitimitásigény fogalma kapcsán nyilván fel kell tenni a kérdést, hogy milyen alapon, milyen típusokat lehet elkülöníteni egymástól. Weber ezt a kérdést nem elemezte, ezért szükség lenne a fogalom explikálására. Ezt az elemzést azonban csak a következő fejezetben fogom elvégezni, miután már bemutattam az uralom legfontosabb típusait.Uralomtípusok
Amikor a Gazdaság és társadalom-ban Max Weber kifejti az uralomtipológiáját, akkor három típust mutat be, a tradicionális, a karizmatikus és a racionális uralmat [weber] Korábbi munkáimban én négyelemű utalomtipológiát használtam [Szaka] [syiDi] de nem igazán támasztottam alá, miért gondolom kiegészítendőnek a weberi tipológiát. Most megpróbálkozom vele. Először röviden vegyük a három klasszikus, weberi uralomtípust. Itt még nem foglalkozom azzal, melyik típus értékelhető korábbinak, alapvetőbbnek a másikhoz képest, és nem reflektálok egyelőre az egymáshoz való viszonyukra sem. Az első típus a tradicionális uralom kategóriája. Íme a jól ismert meghatározás." … elsődlegesen az emberemlékezet óta érvényes tradíciók szentségébe és a tradíciók által autoritással felruházott személyek uralmának legitim voltába vetett mindennapi hiten alapul." [weber]
A definíció kulcsmozzanata a szent tradíció. A tradíciók által autoritással felruházott személyek parancsadási jogosultsága, legitimitása nyilván származtatott jelenség, amit nem érthetünk meg a szent tradíció minősége nélkül, viszont az előbbit már levezethetjük az utóbbiból – mind a fogalom jelentését, mind a jelenség létezését. A tradicionális uralom esetében tehát a tisztázásra váró fogalom a (szent) tradíció kategóriája. A következő uralomtípusként nézzük a racionális uralom fogalmát, amire Weber a következő definíciót húzta rá." … elsődlegesen a legalitásba – a tételes rendnek és a tételes rend által az uralom gyakorlására kijelölt személyek utasítási jogának legális voltába – vetett hiten alapul." [weber]
Ebben az esetben is származtatott kategóriának tarthatjuk az uralom gyakorlására kijelölt személyek parancsadási jogának legitimitását (legalitását), és a definíció központi elemeként a tételes rend fogalmát kell megragadnunk. [♦] Mivel Weber a rend kategóriáján durván a norma fogalmát értette, így az igazi minőséget itt a tételes jelző adja, úgyhogy ezt kell jól megmagyarázni. Azt már érdemes jelezni, hogy az eddigi két uralomtípus középpontjában két rendfogalom áll, hiszen a tradícionális uralomhoz rendelt tradíció is egyfajta rendként (normaként) értelmezhető. A harmadiknak maradt klasszikus weberi uralomtípus a karizmatikus uralom." … elsődlegesen nem mindennapi odaadáson alapul egy szent, hősies vagy példamutató személy, illetve az általa kinyilatkoztatott vagy megteremtett rend iránt." [weber]
A definíció kapcsán először arra hívnám fel a figyelmet, hogy Weber itt sorrendet vált abban az értelemben, hogy előbb beszél az uralmat gyakorló személyekről, és csak azután az uralmi rendről. Ez eddig pont fordítva volt, sőt, az előző két típus esetén azt mondtam, hogy a személyek uralmi jogosítványai levezethetőek az adott uralmi rend érvényességéből. A karizmatikus uralom meghatározásának középpontjába viszont a személy került, és akár tűnhetne úgy is – mégha ez tételesen nincs is kimondva –, hogy itt a személyből lehet a származtatni az általa kinyilatkoztatott rendet. Ezt a váltást, illetve az ebből kibontható fogalmi dimenziót nemsokára elemezni fogom, de előtte még lenne pár megjegyzésem a karizmatikus uralom kapcsán. Van egy fontos definíciós összetevő, a 'nem mindennapi odaadáson alapuló' hit eleme, amit Weber itt alkalmaz először, és csak ekkor lehet észre venni igazán, hogy ez szembeállítható a tradícionális uralomban alkalmazott, ellentétes minősítéssel, a 'mindennapi hitre' való alapozás momentumával. Ez a különbségtétel azért fontos, mert a mindennapiság kontra nem mindennapiság szempontrendszere olyan elemzési dimenziót biztosít, amely mentén később oszályozni tudjuk az uralomtípusokat. Értelmeznünk kell a magának a karizmának a fogalmát is. Ezzel kapcsolatban azt szokás idézni Webertől, hogy a karizmát egyfajta "kegyelmi ajándékként" foghatjuk fel – ami nyilván valamilyen transzcendenciától származhat csak. Amikor Weber meghatározást próbál adni erre a fogalomra, akkor a felsorolásszerű indoklásai közé bevon olyan példákat is, amelyek voltaképp kilógnak a meghatározás hatálya alól, és ezzel kicsit kétértelművé teszi Weber ezt a kategóriát. A karizmáról a következőket írja."»Karizmának« nevezzük egy személyiség nem mindennapinak számító képességeit …, amelyek miatt ezeket a személyeket természetfölötti vagy emberfölötti vagy legalábbis sajátos, nem mindennapi, nem mindenki számára hozzáférhető erőkkel vagy tulajdonságokkal [megáldott] embereknek vagy isten küldöttének vagy példaképnek, s ezért » vezérnek« tekintették." [weber]
Weber itt a karizmatikus uralmat jellemző nem mindennapiságot akarja megragadni, amit – több helyen, itt is, máshol is – érezhető szándéka szerint kirárólagos módon szeretne összekötni a természetfölöttivel, emberfölöttivel. Amikor azonban a fenti felsorolásba beemeli a kivételes (ám – és itt ez a fontos – nem transzcendes minőségű) tulajdonságokra való hivatkozást is, akkor ezzel megszünteti az éles határvonalat a kivételes emberi és az emberfölötti között. Az, hogy mennyire fontos Weber számára a karizma transzcendes eredet, szolgáljon újabb bizonyítékul a következő rövidebb passzus."A karizma akkor érvényes, ha valamiképpen – eredetileg mindig csoda folytán – beigazolódik, s ennek következtében az alávetettek szabadon – csupán a megnyilatkozás iránti odaadásból, a hős iránti tiszteletből vagy a vezér iránti bizalomból – elismerik. De (a valódi karizmánál) ez az elismerés nem a legitimitás alapja, hanem kötelesség …" [weber]
A természetfölötti minőség adja a karizma lényegét, ami mindig csak valami csoda folytán igazolódhat be. De fontos nekünk a fenti idézet egy másik momentuma is, mert segítségével rendbe tehetjük a fent jelzett kétértelműséget. Javaslatom szerint úgy explikálhatjuk a karizmatikus uralomra vonatkozó, eredeti weberi intenciót, hogy Weber meghatározását a következő tézisekre bontjuk: (i) az eredeti karizmatikus uralom transzcendens világképen alapul, (ii) az engedelmeskedni akarás a transzcendenciának való alárendelődési hitből és az annak való megfelelési szándékból fakad, (iii) a karizma a transzcendencia felől érkező kegyelmi ajándék, ami a vezér mint szükségképpen földi személy kiválasztottságát is jelzi egyben a többiek számára, végül (iv) a vezér személyét és utasításait nem annak kivételes képességei miatt ismerik el az emberek, hanem az a hit kötelezi őket a vezér követésre, hogy ő a transzcendencia kiválaszottja, és őt követve voltaképp a transzcendencia akarata szerint járnak el. Ebbe az interpretációba nem férnek bele Weber azon példái, amelyek a vezérek nem mindennapi, de földi eredetű, kivételes képességeire vonatkoznak. Ha jobban megfigyeljük a következő idézetet, akkor kiderül, hogy Pierre Bourdieu is másként értelmezte a karizmatikus uralom fogalmát az eddigiekhez képest."A karizmatikus vezető, ahelyett, hogy – ahogy az a szimbolikus küzdelemben alulmaradottak esetében fennáll – saját maga számára is az lenne, aminek a többiek tartják, eléri azt, hogy az őt vezetővé választó csoport számára is azzá váljék, aminek saját maga véli magát. Ő teremti meg az őt magát megteremtő közvéleményt." [bourd]
Weber példái a nem mindannapi, de földi képességekkel rendelkező vezérekről, Bourdieu nézete a sajátmagát megteremtő karizmatikus vezérről felvetik annak a lehetőségét, hogy esetleg képezhetünk egy új, egy negyedik uralomtípust. Bármennyire is kimondja szószerint és többször is Weber maga, hogy három uralomtípust definál, bármennyire is csak három uralomtípust mutat be az uralom szociológiájában, bármennyire is ugyanezt visszhangozzák a követők Weber óta, maga Weber az, aki tesz egy olyan gesztust a Gazdság és társadalom egy pontján, amit értelmezhetünk úgy, mint egy tétova kísérletet a negyedik uralomtípus elkülönítésére vonatkozóan. Az uralom szociológiájáról szóló fejezet hetedik pontjának címe A karizma uralomellenes átértelmezése, és erről a következőeket Weber a fejezet kezdő paragrafusában."Az elsődeges értelme szerint a tekintélyuralmat megalapozó karizmatikus legitimitáselv olyan értelmezést is kaphat, amelyben már nem a tekintélyuralmat támasztja alá. A karizmatikus tekintély tényleges érvényessége ugyanis valójában teljes egészében azon múlik, hogy karizmája » beigazolódik-e«, mert ez a feltétele annak, hogy az alávetettek elismerjék, ami persze a karizmatikus képességekkel rendelkező és ebből következően legitim úrral szemben kötelességük. A szervezeti kapcsolatok növekvő racionalizálása esetén azonban kézenfekvő, hogy ezt az elismerést már nem a legitimitás következményének, hanem e helyett a legitimitás alapjának fogják tekinteni … s végül a közösség részéről történő elismerést úgy fogják föl, mint » választást«." [weber]
Mivel mindez a karizmatikus uralomról szóló fejezetbe van ágyazva, mondhatnánk azt, hogy itt továbbra is csak a karizmatikus uralomról van szó. Weber nem mondta ki, hogy ő úgy értelmezi a fenti részt, mint amelyben egy új, önálló uralomtípust vezetne be. Ebből következően nyilván nem mondhatom, hogy Weber négy típusról beszélt (vagy akart volna beszélni). Ennek ellenére érvelni fogok az elkülönítés mellett, és javaslom felvenni az újabb kategóriát, mert ha így teszünk, konzisztensebb és hézagmentesebb uralomtipológiához jutunk az eredeti hármas felosztáshoz képest. Weber ugyanis úgy jellemzi a átértelmezett karizmatikus uralom kategóriáját, ami egyrészt szöges ellentétben áll egy adott dimenzióban az eredeti karizmatikus uralom jelentésével, másrészt viszont egy kétdimenziós fogalmi térben értelmezve látványosan ki is egészíti azt, ami nélkül hiányos lenne, amivel együtt viszont teljessé válna az uralomtípusok felosztása, vagyis pótolni lehetne vele a "hiányzó láncszemet". A megoldás felé elindulva elsőként idézzük fel azt a tényt, hogy Weber az uralomtípusokat a hozzájuk kapcsolható legitimitásigény alapján tartotta elkülöníthetőnek egymástól." … célszerű az uralom fajtáit a rájuk jellemző legitimitásigény szerint megkülönböztetni. … Itt az a mérvadó, hogy maga az uralom milyen fajta legitimitásra tart igényt, és saját legitimitásigénye releváns mértékben érvényesül-e …" [weber]
Ez a weberi tipizálási javaslat teljesen érthető és elfogadható, ha belegondolunk abba, mi az uralom lényege. Valaki kiáll egy másik ember elé, és megfogalmaz egy parancsot a másiknak. A parancsot kiadó félben ott van az igény arra, hogy a másik ember teljesítse a kiadott parancsot, és a parancsolónak ezzel párhuzamosan fel kell készülnie arra is, hogy milyen érveket sorakoztathatna fel abban az esetben, ha a másik oldalon vitatnák az ő parancsadási igényét. Az, hogy milyen típusú érvekkel tudná, akarná megvédeni saját uralmi igényét, leginkább attól függ, hogy milyen érvényességfogalommal rendelkezik saját felhatalmazottságára vonatkozóan. Weber ezt nevezi legitimitásigénynek. Ha a legitimitásigény alapján határozhatjuk meg az uralomtípusokat, akkor nyilván meg kell tudnunk mondani azt, hogy milyen szempontok szerint lehet a legitimitásigény fogalmának típusait megalkotni. Két dimenziót javaslok figyelembe venni itt, amelyek segítségével konzisztens módon értelmezhetjük az általam javasolt négyes felosztást az uralom fogalmára vonatkozóan. Émile Durkheim a társadalmi jelenségek magyarázata során elkülönített két fontos kategóriát, a szent és a profán fogalmát. Ez a fogalomkettős segíthet minket a normativitás és az uralom értelmezésében, valamint az uralom tipizálásában egyaránt. Durkheim így ír a két fogalomról." … a szentet a profánhoz viszonyítva már csakis különneműségük alapján határozhatjuk meg. E különneműség azért elegendő a dolgok ezen osztályozásának jellemzéséhez és az összes többitől való megkülönböztetéséhez, mert igen sajátos: abszolút. Az emberi gondolkodás történetében nincs még egy példa a dolgok ennyire mélyen különböző, ennyire ellentétes két kategóriájára." [Emile]
Durkheim ezt a kettősséget tartja a leginkább egymást kioltó fogalmi minőségnek, amihez képest például a jó és rossz vagy az egészség és betegség közti viszony jóval enyhébb szembenállást jelent. Utóbbiakban ugyanis van valami közös. A jó és rossz fogalma az erkölcsiség két ellentétes minősége ugyan, de mindkettő az erkölcs kategóriája alá sorolható be, ennyiben valamilyen minimális közös vonásnak léteznie kell mindkettejükben. Ezzel szemben ami szent vagy ami profán, abban nincs semmi közös."Amikor azt állítjuk róluk, hogy szentek, ezen azt értjük, hogy értékük nem mérhető össze a többi értékkel. Szent az, amit elkülönítettek, aminek nem lehet közös mértéke a profánnal." [durkh]
Van tehát két fogalmunk, amelyekkel jelezhetünk, összeköthetünk egy-egy világot, egy-egy világnézetet is. Mindazon társadalmak, amelyeknek a tagjai domináns módon transzcendens világképpel rendelkeztek, a szent, a szentség minőségével kapcsolták össze az uralmi kapcsolataikat (mint minden más egyebet is). Ezzel szemben azokban a társadalmakban, amelyekben a transzcendenciában való hit legalább abból a szempontból megszűnt, visszaszorult, hogy az emberek közti uralmi igények indoklásai során nem hivatkoz(hat)tak a földöntúli akaratokra, ott az uralmi kapcsolatokat a – szentséggel élesen szembenálló – profán minőség jellemez(het)te. Ez a dichotómia adja az uralmi osztályozáshoz szükséges egyik fogalmi dimenziót. A tradicionális és karizmatikus uralom érvényességi igényei esetében lehet hivatkozni emberfeletti akaratokra vagy földöntúli akaratokra is, a racionális és átértelmezett karizmatikus uralom esetében nem. Utóbbiakban csak az emberi akaratokra való hivatkozást fogadják el érvényesnek. Ennek nagyon fontos következménye az, hogy amíg az emberi akaratokra hivatkozó szabályokat mindig meg lehet támadni, mindig lehet vitatkozni fölöttük, addig a emberfeletti akaratokra épített, pontosabban azokra hivatkozó szabályokat sosem lehet nyíltan támadni. [♦] (☜) A másik fogalmi dimenziót úgy találhatjuk meg, ha felidézzük, hogy milyen módon szólt Weber az uralom rend vagy uralmi szabályok, illetve az uralmat gyakorló személyek viszonyáról, "sorrendiségéről". Felhívtam rá a figyelmet korábban, hogy a tradícionális és a racionális uralom meghatározásakor Weber az uralmat gyakorló személyekhez képest előbbre vette, bizonyos értelemben fontosabbnak tartotta a parancsadási lehetőségeket rögzítő, azokat folyamatosan megteremtő szabályokat, rendtípusokat, a tradíciót, illetve a tételes rendet. Ezzel szemben a karizmatikus uralom definíciójában megcserélte ezt a sorrendet, és a vezér személyét tette a fogalom központjába mint olyan fogalmi összetevőt, amelynek ismeretében már levezethető az általa kinyilatkoztatott rend, szabály is. Ugyanezt természetesen elmondhatjuk az átértelmezett karizmatikus uralomra vonatkozóan is. A nagy kérdés itt az, hogy milyen címkékkel, milyen leírással láthatjuk el ezt a dimenziót, amely tehát egyik oldalra teszi a tradicionális és racinális uralmakat, amelyeket a központba tett szabállyal, rendtípussal azonosíthatunk, míg a másik oldalra sorolja a személyeket előtérbe helyező kétféle karizmatikus uralmat. Értelmezésem szerint az a legáltalánosabb közös része ennek a kétféle besorolásnak, hogy valamely uralomban milyen módon lehetséges a parancsadási lehetőségeket, az uralmi szabályokat, különösen azok tartalmát megváltoztatni. A tradicionális uralomban nincs, vagy alig van, vagy csak trükkösen van mód megváltoztatni a tradíciókba lefektetett szabályokat, de amilyen mértékben ez mégis lehetséges, úgy mindig a tradíciókra, tehát a szabályokra magára hivatkozva lehet ezt megtenni. Ugyanez igaz a racionális uralomra is, csak ott az érintettek által korábban lefektetett, tételes rend (általában a jogszabályok) újbóli tételezésén keresztül lehet változtatásokat elérni. Mindkét esetben az a közös, hogy a szabályváltoztatás a szabályok (újra)értelemzésén keresztül történik. Ezzel szemben a karizmatikus uralmak esetében a személyt kell változtatni ahhoz, hogy az uralom jellege megváltozhasson. A karizmatikus uralomban mindig van egyfajta "önkény" abban az értelemben, hogy elválaszthatatlan tőle a vezér személyéhez való kötöttség, önkényesség. Jézus paradigmatikus példáját idézve: "Hallottátok, hogy a régiek ezt a parancsot kapták:… Én pedig azt mondom nektek …" [szent] Amíg a vezért követik az önkéntesek, addig mindig beszélhetünk önkényességről. Ebben a viszonyrendszerben az uralom jellegének, az uralmi szabályok megváltoztatásának nincs más módja, mint a vezér személyének lecserélése. A két most bevezetett dimenziót egyszerre figyelembe véve konzisztens osztályozási lehetőséghez jutunk, amit az alábbi táblázatos formában írhatunk fel [Szaka]| &\multicolumn{2}{c}{az uralmi szabályok változtatásnak módja:}\\ | ||||||||||||||
| {a legitimititásigény indoklásakor:} | szabályértelmező | személycserélő | ||||||||||||
| emberfeletti akaratra is hivatkoz(hat)nak | tradicionális | karizmatikus | ||||||||||||
| csak emberi akaratra hivatkoz(hat)nak | racionális | átértelmezett karizmatikus | ||||||||||||
| &\multicolumn{2}{c}{az uralmi szabályok változtatásnak módja:}\\ | ||||||||||||||
| {a legitimititásigény indoklásakor:} | szabályértelmező | személycserélő | ||||||||||||
| emberfeletti akaratokra (is) hivatkoznak | zártrendű | karizmatikus | ||||||||||||
| csak emberi akaratokra hivatkoznak | racionális | átértelmezett karizmatikus | ||||||||||||
"A tradíciókhoz köthető korszakokban a karizma jelenti a nagy forradalmi erőt. Eltérően a másik, ugyancsak forradalmasító erőtől, a » ratio«-tól amely vagy egyenest kívülről hat – úgy, hogy megváltoztatja az életkörülményeket és az életproblémákat, és ezzel közvetve a hozzájuk való viszonyulást is – vagy azon keresztül hat, hogy intellektualizálja a problémákat, a karizma kínból vagy lelkesedésből fakadó belső átalakulást tud előidézni, amely különféle viszonyulásokban – minden egyes életformához és általában a » világhoz« való viszonyulásban – kialakuló tökéletesen új beállítottság hatása alatt teljesen megváltoztatja a leglényegesebb érzületi és cselekvési irányokat." [weber]
Webernek természetesen igaza van akkor, amikor azt állítja, hogy a tradíciókhoz képest a ráció is lehet forradalmasító erő abban a közvetett értelemben, ahogy azt Weber leírja, de a karizmatikus uralom érzelmi alapjait, a kínből és lelkesedésből fakadó belső átalakulás mozgosító, forradalmi erejét ugyanúgy érdemes kiterjeszteni az átértelmezett karizmatikus uralomra vonatkozóan is. Ha viszont az átértelmezett karizmatikus uralmat is figyelembe vesszük ebben a közös értékelésben, akkor mondhatjuk azt, hogy a modern vezérek megjelenése, létezése ugyanolyan forradalmasító potenciállal bír a racionális uralommal, mint a hagyományos karizmatikus uralom a tradicionálissal uralommal szemben – és az okok természetesen ugyanazok mindkét esetben. E tézis további alátámasztásra érdemes felidézni azt, amit a racionalitás és az érzelmek, vágyak, késztetések egymáshoz való viszonyáról (arról, hogy a racionalitás önmagában nem rendelkezik mozgósító erővel) írtam korábban (☜) A gondolatmenet lezárásaként annyit jegyeznék meg, hogy történelmileg is, fogalmilag is az a legvalószínűbb, hogy a karizmatikus uralom jelent meg legelsőként az emberek között, majd idővel valamelyik karizmatikus uralom emlékeire már úgy hivatkoztak, hogy a tényleges uralomgyakorlás formái egyre inkább a tradicionális uralomra kezdtek hasonlítani. A racionális uralom a világ varázstalanításával párhuzamosan terjedt el, majd kezdett idővel dominássá válni. Ahogy megjelent a racionális uralom és elkezdte a kinevezés elvén álló, hierarchikus uralmi szerkezetekbe rendezni az uralmi viszonyokat, úgy jelent meg – szükségszerűen – az az igény, hogy a hierarchikus szerkezetek csúcspontjain levő pozíciókba, amelyeket nem lehet(ett) a kinevezés elve alapján betölteni, a (személy)választás elvét alkalmazva keressenek megfelelő – karizmatikus képességekkel rendelkező – személyeket.Hatalom és uralom viszonya
Korábban már explikáltam a hatalom fogalmát (☜) ebben a fejezetben bemutattam a norma és az uralom kategóriáit, így minden adott, hogy megpróbáljam tisztázni a köztük levő kapcsolatot. Emlékezzünk rá, hogy a hatalom definiálásakor a két szembenálló fél ellentétes akaratáról volt szó, és ez a két konfliktusos akarat ugyanarra a cselekvésre irányult. Ez utóbbi kötötte őket össze, és ezen az alapon lehet egyáltalán a köztük levő konfliktusról beszélni. Az A személy áll az ajtóban, mire egy másik ember odalép, B rászól, hogy álljon félre az útból, mert szeretne bemenni. Ha A nem akarja B-t beengedni mondván, hogy ő a bank biztonsági őre, és a bank még nem nyitott ki, akkor megállapíthatjuk, hogy akaratkonfliktus van köztük. Ennyit elmesélve még nem tudhatjuk, hogy a hatalom vagy az uralom jelenségéről van-e szó. Amennyiben B előránt egy pisztolyt, és A-nak szegezve követeli a banki trezorban levő pénzt, akkor már megállapíthatjuk, hogy hatalomról beszélhetünk – már amennyiben a rablás sikeres lesz. A lényeg az, hogy a hatalom megvalósulásához kényszer alkalmazására volt/van szükség. Ehhez képest nagyon más logika mentén működik az uralom jelensége. Weber alapján azt mondtuk, hogy az uralomhoz mindig kell engedelmeskedés, amit a hatalom esetében nem találtunk. De mit is jelent az engedelmesség?"Az » engedelmesség« azt jelenti, hogy az engedelmeskedő személy cselekvése úgy megy végbe, mintha az illető a parancs tartalmát pusztán a parancsért tette volna a viselkedése maximájává, s csakis a a formális engedelmességi viszony miatt tett volna így, függetlenül attól, hogy mi a saját véleménye a parancsról mint olyanról, értékesnek tartja-e vagy sem." [weber]
Az uralom vagyis a más által kiadott parancsnak való engedelmeskedés azért valósul meg, mert az alávetett fél elfogadja a másik parancsadási jogosultságát. Ez azt jelenti, azt kell, hogy jelentse, hogy az alávetett félnek adott esetben önként, kényszer nélkül is fel kell tudnia adni saját akaratát azért, hogy végrehajtsa a kiadott parancsban foglaltakat. Könnyen elképzelhető, hogy a parancskiadás pillanatában a parancs tartalmával ellentétes akarattal rendelkezik, de ezt – ha uralomról van szó – figyelmen kívül kell hagynia. Az előző banki példára utalva: lehet, hogy B személy azért akar bemenni a bank ajtaján, mert ő az új főnök, és ezt még a biztonsági őr nem tudja. Ebben az esetben B-nek nem kényszer alkalmazására van szükség, hogy bejusson, hanem nyilvánvalóvá kell tennie azt A felé, hogy ő az új fiókvezető, és abban a pillanatban, ahogy ez sikerül neki, az őr már feladja saját korábbi – a beengedést tiltó – akaratát. Kétféle módon is lehetne interpretálni azt a tényt, hogy a biztonsági őr megváltoztatja az akaratát. Mondhatnánk azt, hogy a cselekvést megelőző mérlegelése során erősebb érvnek bizonyult a főnök státusának felismerése az illetéktelenek beengedésére vonatkozó tiltás, vagyis az akaratokat kezelhetnénk úgy, mint amik ugyanazon a szinten helyezkednek el. Ezzel szemben pontosabbnak tartom azt az értelmezést, amely szerint az uralmi helyzet felismerése egy másodrendű akarat megjelenését okozta, ami a személy eredeti, elsőrendű akaratát mintegy zárójelbe tette, felülértelmezte. Ez a jelenség teljesen analóg a jogosultságok és kötelezettségek rendszerében belül elkülönített első- és másodrendű fogalmak egymáshoz viszonyulásával (☜) A helyzet uralomként való (át)értelmezése azért következett be, mert a biztonsági őr a belépni kívánkozó emberben a főnökét felismerve felhatalmazottság tartalmú jogosultságot tulajdonított neki, amivel szemben benne egy beavatkozásnak kitettség tartalmú kötelezettség keletkezett, és e másodrendű késztetés hatására megváltoztatta saját korábbi elsőrendű akaratát. Az analógia csak annyiban nem mondható száz százalékosan megalapozottnak, hogy az uralom esetén akaratokról, a perszonális pozícióknál pedig jogosultságokról és kötelezettségekről beszélünk. De ezen az eltérésen túl a szerkezeti hasonlóságot teljesnek ítélhetjük. A hatalom és uralom kategóriáját – bármennyire is hasonló jelenséget írhatunk le velük – szigorúan el kell választanunk egymástól. Így tette ezt egyébként maga Weber is. Erre természetesen a legfontosabb bizonyíték az, hogy eleve különböző fogalomként definiálta őket, és az uralom szociológiáját messze külön kezelte a gazdasági hatalom kérdésétől. De az alábbi idézetben explicit módon figyelmeztetett arra, hogy a két jelenséget nem szabad összemosnunk."Másfelől viszont a monopolhelyzetből származó gazdasági » hatalmat«, vagyis azt a lehetőséget, hogy az egyik cserepartner » diktálja« a csere feltételeit a másiknak, önmagában véve még nem nevezzük » uralomnak«, mint bármilyen más – teszem azt az erotikában, a sportban, a vitában, vagy egyebütt élvezett – fölényből eredő » befolyást«." [weber]
A hatalom fogalmának tárgyalásakor bemutattam az a folyamatábrát (☜) ami az uralom értelmezésében is segíthet. Amikor ugyanis az elsőrendű akaratok különbsége, konfliktusa nyilvánvaló válik a kapcsolat résztvevői számára, akkor az lesz a nagy kérdés, hogy milyen gyakorlati érveket szolgáltat a kapcsolat domináns szereplője. Amennyiben valamilyen létező, legitimnek tartott normára mutat rá, amely az ő parancsadási igényét alátámasztja, és az alávetett fél ezt elfogadja, akkor uralmi helyzetről beszélhetünk. Ez jelenti a döntő különbséget a hatalom és uralom között. Az uralmi igény alátámasztására mindig kell valamilyen norma, a hatalomhoz ez sosem szükséges. Ennek következményeként a hatalomgyakorlást mindig méltánytalannak érzi az azt elszenvedő fél, míg a normakövetésből eredő engedelmeskedni akarás nem jár együtt a méltánytalanságérzet kialakulásával.Közösségi döntések
A kő kicsorbítja az ollót.
Az olló elvágja a papírt.
A papír becsomagolja a követ.
Aggregálás mint közösségi döntési technika
Amikor a közösségi döntésre gondolunk, elsőre valóban a választás/szavazás technikája ugrik talán mindenkinek, de az induláskor nem árt leszögezni, hogy azért nem ez az egyetlen módszer arra, hogy közösség kitermeljen magából egy közösségi döntést a közösség tagjainak egyéni teljesítményeire támaszkodva. Csak jelzésszerűen, anélkül, hogy ismertetném az egyes lehetőségeket, felsorolok pár aggregálási, közösségi döntési technikát. A közösségi döntési módszer alapulhat az egyének közti harcon (combat), versengésen, versenyen (contest) vagy a tagok közti alku(dozás) (bargaining) folyamatán. Dönthet egy közösség úgy, hogy a tagok közti eszmecserét, tárgyalást (discussion on merits) addig tartja fent, amíg egységes vélemény ki nem alakul közöttük, de gyorsabban elintézheti a döntést, ha a szavazás (voting) vagy a véletlen sorshúzás (chance) technikáját alkalmazza. Végül igazodhat egy közösség valamilyen autoritatív eljárás (authoritative determination) során született döntéshez is. A társadalmi választások elméletének fókuszában az a folyamat áll, amelynek keretében (és eredményeként) az egyéni választásokból (döntésekből) közösségi választás (döntés) lesz valahogy. Közösségi döntést egyéni döntésekből többféleképpen lehet "csinálni". A történelmileg leggyakoribb megoldás a döntési privilégium kialakítása és fenntartása, amikor egy társadalmi norma kijelöli az emberek valamely körét, akiknek a kezébe teszi a közösség egészét érintő döntés jogát. Ezt a lehetőséget - bármennyire is fontos a történelemben - itt nem vizsgáljuk. A másik közösségi döntési mód az érintettek közötti konszenzus megteremtése: olyan mechanizmus kidolgozása és működtetése, amelynek révén mindenki ugyanazt a döntést fogadja el egységesen. Mivel ez a döntési mechanizmus nagyon erős feltételen nyugszik, hisz a konszenzus megteremtése sokszor nagyon idő- és energiaigényes folyamat, a módszer fontos eszköze a vétó technikájának alkalmazása. A teljes pozitív konszenzus eléréséhez képest gyengébb a negatív konszenzus, amikor ha nem is teljes mértékben értenek egyet a felek, de legalább nem ellenzik a vita során javasolt dolgokat. Hogy ilyen alkalmak során ne lehessen eltérni a konszenzus követelményétől, a vétójog az utolsó eszköz az egyet nem értők kezében. A konszenzusos döntések fontos típusát jelentik a kompromisszum alapú döntési eljárások, amelyekről Max Weber mint kompromisszumtestületekről ír [weber] A kompromisszum elve "gyengített" konszenzus elvként minősíthető, és akkor alkalmazzák, amikor azonos társadalmi szerepek mentén csoportosuló emberek meg kell, hogy egyezzenek egymással úgy, hogy a csoportok (vagy azok képviselői) között fenntartják a konszenzus elvét, de a csoport tagjai egyénileg valamennyien már nem nem vesznek részt a vitában. A kompromisszumtestületek működésére az érdekképviseleti szervek (állami szervek, munkaadók, illetve munkavállalók képviseleti szervei) közti tárgyalások szolgáltatják a legjobb példát. Ilyenkor a döntéshozó testületnek olyan konszenzusos döntést kell hoznia, ami minden oldal számára elfogadható, ami szinte mindig valamilyen kompromisszum eredménye. A kompromisszum jelenségét találjuk meg a stratégiai szavazás, azon belül is a szavazatcsere intézménye mögött (☜) Amikor mindenki egyenrangú félként beleszól(hat) a közös ügyek megvitatásába, akkor már szavazótestületekről, szavazás alapú döntéshozatalról beszélhetünk. Itt mindig valamilyen többségi elv alapján születik a döntés úgy, hogy valamilyen szavazási eljárással összegzik az egyéni véleményeket egyetlen közösségi döntéssé. A továbbiakban erről a közösségi döntési módszerről lesz szó.A szavazás elve
A szavazás tehát a közösségi döntéshozatal egyik fontos, bár nem kizárólagos módszere. A szavazásra jogosult szavazók leadják a szavazataikat és egy összegző eljárás segítségével közös döntést hoznak ki – ezt jelenti a szavazás fogalma. Az egész döntési folyamatban sok elemzendő kérdés van, amelyek közül párat később még tárgyalni fogok. Bármennyire is fontos kérdés, hogy pontosan milyen is a szavazási eljárás menete, hogyan bonthatjuk fel összetevőkre a szavazás folyamatát, itt nem foglalkozom ezzel. Létezik egy "bonyolult", sok összetevős és sok lépésből álló folyamat, amely az emberek fejében levő sok-sok egyéni véleményt valahogyan egyetlen közösségi véleménnyé aggregálja. Ehhez először a véleményt szavazattá kell alakítani, aztán – olykor, ha szükséges – a véleményt polarizálni kell (eközben preferencia esetén azt kell figyelni, hogy az egyén mit preferál, faktuális vélemény esetén azt, hogy hogyan vélekedik). Előfordulhat az is, hogy a (binárisan polarizált) véleményeket súlyozni szükséges. A folyamat végén valamilyen algoritmus szerint összegezni kell az egyéni szintű adatokat. Sok technikai kérdést lehetne vizsgálni, de nem teszem. A teljes szavazási folyamatot le lehet írni pontos képletekkel, formulákkal. A választások elméletéről matematikailag nagyon jól megalapozott szakkönyvek születtek, úgyhogy én kihagyom ezt a kérdéskört. Ami egy cselekvéselmélet számára fontos lehet, azt megemlítem itt-ott, a részletek pedig már nem az emberről szólnak, hanem a technikáról. Ebben a könyvben ez másodlagos. Azzal sem foglalkozom, hogy milyen szavazási eljárások, szabályok, algoritmusok léteznek. Alan D. Taylor vagy húsz szavazási szabályt mutat be alaposan a könyvében [Taylo] Korábban Mészáros József kollégámmal együtt mi is összeállítottunk egy könyvecskét erről, ott sok részlet olvasható e tárgyban [Mszro] E könyv alapján mutatok be egy összefoglaló ábrát a legismertebb választási eljárásokról.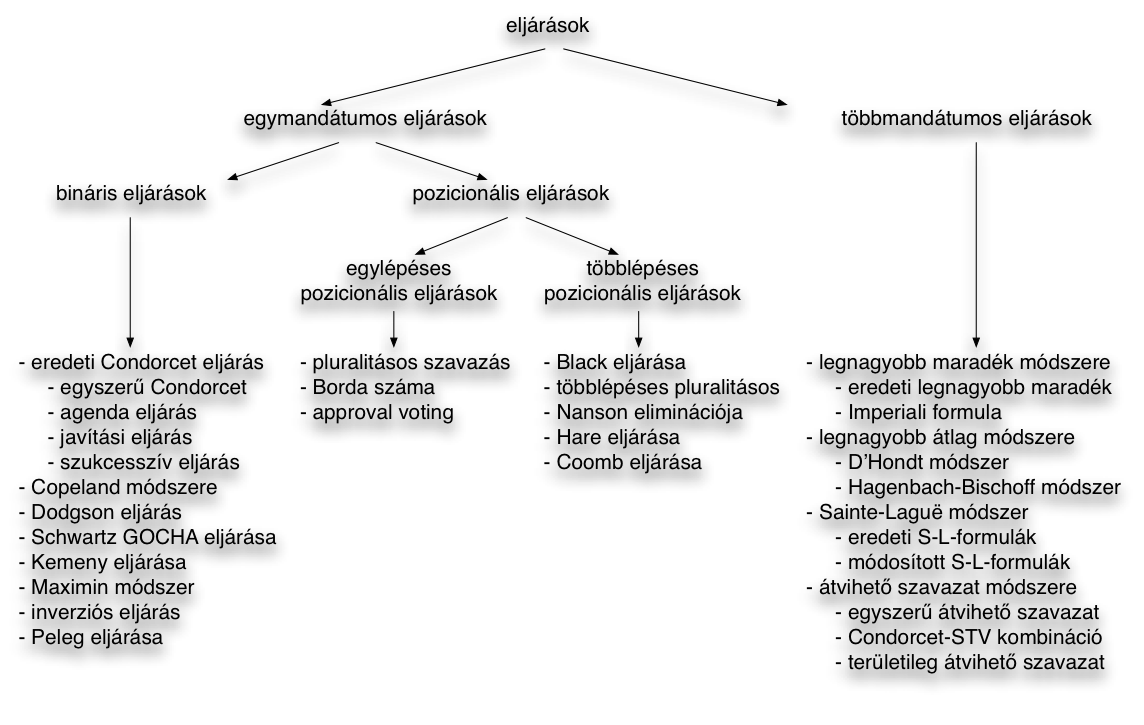
Nem állítom, hogy az ábra kimerítően bemutatná az összes fontos algoritmust. Vannak, akik másként csoportosítanák az eljárásokat. Az egészből csak azt tartom lényegesnek, hogy az ábra azt mutatja, nincs is olyan sok szavazási eljárás. Arra a kérdésre, hogy mit is kell aggregálni a közösségi döntések során, a legáltalánosabban adható válasz az, hogy véleményeket, amiből fakadóan a társadalmi választások elméletét tarthatjuk a véleményaggregálások elméletének is. A vélemények aggregálásának gyakorlati szempontból tekintve két ága, két fajtája létezik. Előfordulhat, hogy:
- egy személy több, különböző értékelési szempontok szerint képzett véleményhalmaza alapján kell egyetlen aggregált döntést hozni, vagy az, hogy:
- több személy véleményhalmaza alapján kell egyetlen aggregált döntést hozni.
- milyen problémák, paradoxonok keletkez(het)nek a véleményaggregálás (judgement aggregation) folyamata során;
- milyen társadalmi elvárásoknak, feltételeknek lehet (illetve nem lehet) egyszerre megfelelni a preferenciaaggregálás (preference aggregation) folyamata során;
- milyen hatása van az aggregálási eljárásoknak a folyamat végeredményre;
- milyen módon lehet biztosítani az egyéni megnyilatkozások őszinteségét (sincerely voting) vagy másként a csalásbiztosságot, illetve hogyan lehet kezelni (ha kell, elkerülni) a stratégiai vagy taktikai szavazást (strategic or tactical voting).
$\mathscr{L}_{AL}$($\mathscr{L}_{PL}, \mathbb{S}, \mathbb{A}, \Phi, \mathbb{C}, \{x,y,z\}, \{\alpha, \beta, \gamma\}, \rel{F})$
| $\mathscr{L}_{PL}$ | propozícionális logika |
| $\mathbb{S}$ | világállapotok halmaza |
| $\mathbb{N}$ | ágensek halmaza |
| $\Phi$ | vélemények halmaza |
| $\mathbb{C}$ | választások halmaza |
| \rel{F} | választási függvény |
$\mathbb{N} = \{1, \dots, i, \dots, |\mathbb{N}|\} $, ahol $|\mathbb{N}|$ a szavazók száma
szavazók halmaza (hun) – set of voters (eng) – set of individuals (eng)
$\mathbb{X} = \{m,n,\dots, o \} $
választható (világ)állapotok (hun) – conceivable (social) state (eng)
$\phi_i \equiv \rel{R}_i \;|\; \rel{P}_i \;|\; \rel{I}_i$
egyéni preferenciarendezés (hun) – egyéni vélemény (hun) – voter's preference (eng) – individual's opinion (eng)
$\{\rel{R}_i\}_{i\in \mathbb{N}} \defi \{\rel{R}_1, \rel{R}_2, \dots, \rel{R}_{|\mathbb{N}|} \} \equiv \{\phi_i\}_{i\in \mathbb{N}} \equiv \{\phi_1, \phi_2, \dots, \phi_{|\mathbb{N}|} \}$
egyéni preferenciarendezések halmaza (hun) – véleményhalmaz (hun) – set of voters' preferences (eng) – set of individuals' opinions (eng)
$a \defi \langle \rel{R}^a_1, \;\dots\;, \rel{R}^a_i, \;\dots\;, \rel{R}^a_{|\mathbb{N}|} \rangle \equiv \langle \rel{R}^a_i \rangle_{i \in \mathbb{N}} \equiv \Phi \equiv \langle \Phi_i \rangle_{i \in \mathbb{N}} \equiv \langle \phi_k, \dots, \phi_m \rangle$
(preferencia)profil (hun) – véleményprofil (hun) – (preference) profile (eng)
$\rel{F}(a) \equiv \rel{F}(\langle \Phi_i \rangle_{i \in \mathbb{N}}) \equiv \rel{F}(\langle\rel{R}^a_i \rangle_{i \in \mathbb{N}})\defi C(\langle \rel{R}^a_i \rangle_{i \in \mathbb{N}}) \equiv C^a \equiv \rel{F}: \mathbb{D}_F \mapsto \mathbb{X}$, ahol $\mathbb{D}_F \subseteq \mathbb{X}^{|\mathbb{N}|}$
közösségi vélemény függvény (hun) – csoportdöntési fügvény (hun) – group decision function (eng) – társadalmi jólét függvény (hun) – social welfare function (eng) – preferenciaaggregálási függvény (hun) – preference aggregation function (eng) – constitution (eng) – közösségi preferencia (hun) – social preference (eng) – kollektív választás(i szabály) (hun) – collective choice (rule) (eng) – kollektív döntés(i szabály) (hun) – collective decision (rule) (eng) – allokációs mechanizmus (hun) – allocation mechanism (eng) – (társadalmi) választási függvény (hun) – (social) choice function (eng) – társadalmi döntési módszer/függvény (hun) – social decision method/function (eng) – szavazási rendszer (hun) – voting system (eng) – voting scheme (eng) – voting mechanism (eng) – social choice procedure (eng)
Bár a közösségi döntések elméletében mindig abból indulunk ki, hogy a közösségi döntést az egyéni döntések, preferenciarendezések határozzzák meg, az elmélet középpontjában nem annyira az egyéni rendezések, hanem inkább az egyéni rendezések, egyéni véleménynyilvánítások halmaza, de még inkább rendezett struktúrái állnak. Ezeket nevezzük profiloknak, és a későbbiekben ezekre hivatkozva tudjuk megadni a legfontosabb fogalmak definícióját. A bemutatandó elmélet javarésze a preferenciaaggregálások kérdéseivel foglalkozik, ezért a legtöbbször a preferenciarendezésekre utaló jelöléseket fogom használni, de a végefelé szóba kerülnek a véleményaggregálás problémái, és akkor majd váltani fogok egy általánosabb jelölésmódra. Az alapfogalmak bevezetése után érdemes egy közös ábrában is feltüntetni a most jellemezni kívánt aggregálási folyamat legfontosabb összetevőit, az ezek közti kapcsolatokat.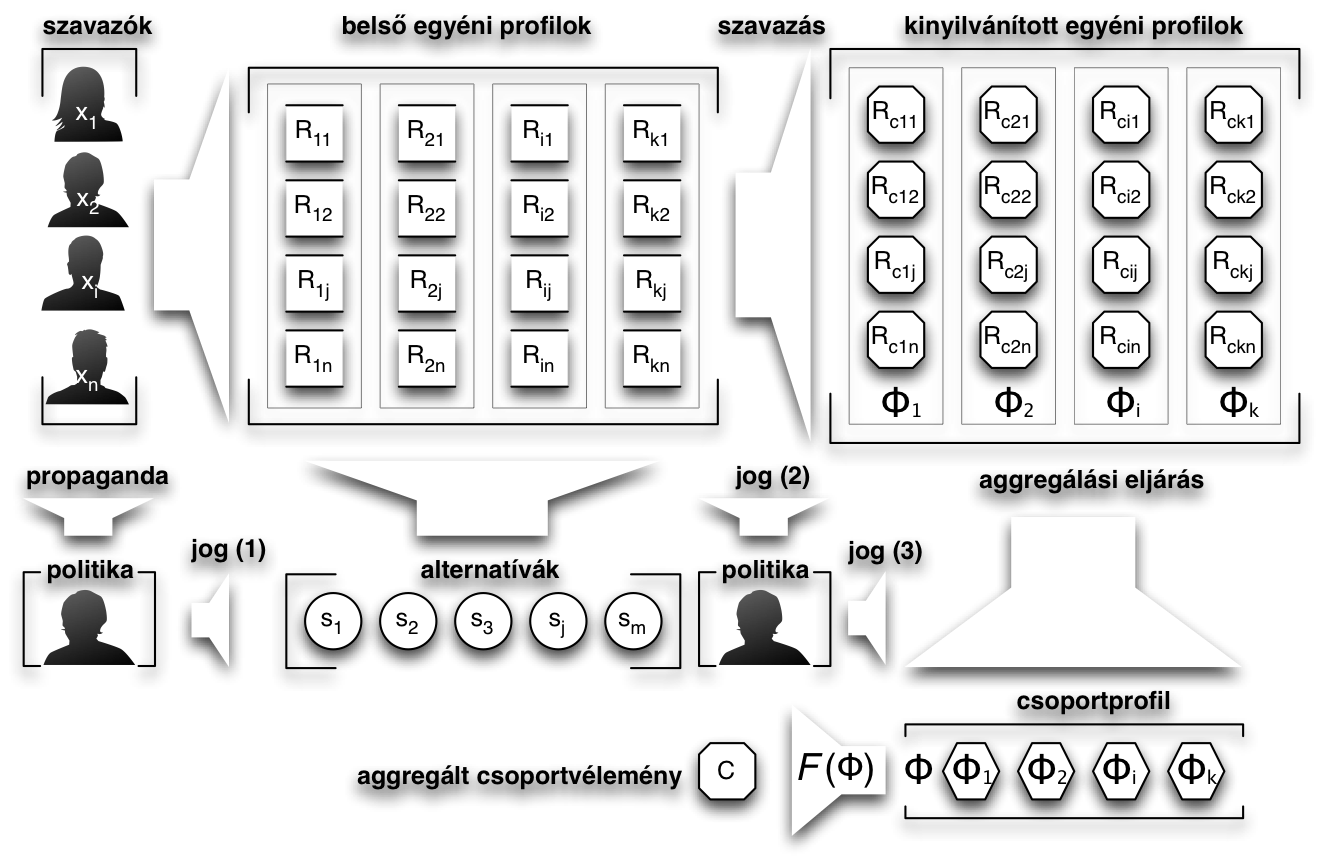
A helyzet legfontosabb viszonya az egyének és a világállapotok közti kapcsolat, amelyről itt semmit sem tudunk mondani. Tényként vesszük itt tudomásul, hogy egy adott csoport tagjai kifejezik a véleményüket a világállapotok valamely halmazáról. Attól függően, hogy melyik véleményaggregálási helyzetben vannak, más lesz az egyéni vélemények típusa. Az egyéneknek véleményük lehet a világállapotok kívánatosságáról, amit preferenciarendezés formájában fejezhetnek ki, de véleményük lehet a világállapotokra vonatkozó faktuális kijelentés is. Ezek az egyéni vélemények – alapértelmezés szerint – még őszinték, viszont nem nyilvánosak abban az értelemben, hogy az ágensek nem nyilvánították ki őket valamilyen szavazási aktus keretében. Ha ez a szavazás megtörténik, akkor beszélhetünk az ágensek kinyilvánított véleményeiről, és ezeket az ágensekhez rendelve megkapjuk a külső egyéni profilokat. A szavazás aktusában lehet megragadni a stratégiai szavazás jelenségét. A külső egyéni profilok alapján lehet létrehozni a csoportprofilt, majd ez alapján a közösségi döntés végeredményét. Az aggregálási eljárás – szűkebb értelemben vett – fogalma ezt a véleményösszesítési folyamatot ragadja meg. Ez az ábra az aggregálási folyamat legáltalánosabb értelmezését jelenti. Magába foglalja az aggregálási feladatok mindkét ágát, a vélemény- és a preferenciaaggregálás jelenségét. A következő két nagyobb fejezetben bemutatom mindkét területet, előbb a preferenciák, majd a vélemények aggregálásának mikéntjét. Mivel a társadalmi választások elmélete 50-60 éven át a preferenciák aggregálásának kérdéseivel foglalkozott, és igazából csak a 2000-es években kezdték el vizsgálni a faktuális ítélek aggregálásának kérdéseit, így az előbbi témáról sokkal több ismeret felhalmozódott. Ennek köszönhetően én is sokkal többet foglalkozom a preferenciaaggregálás területével.
Preferenciaprofilok tipológiája
Ha az egyéni preferenciák helyett társas vagy közösségi preferenciákat vizsgálunk, akkor az egyéni preferenciák valamely összességét preferenciaprofilnak hívjuk. Ezek a preferenciaprofilok rendelkezhetnek olyan tulajdonságokkal, amelyekre támaszkodva fontos és érdekes tételek vezethetők le. Ebben a fejezetben ezeket a speciális mintázattal rendelkező profilokat mutatom be, de itt nem foglalkozom a belőlük levezethető tételekkel. Amikor preferenciaprofilokat jellemzünk, akkor nemcsak az összahasonlítandó alternatívákra vonatkoztatjuk az állításainkat, de a minősítésbe bevonjuk a preferenciarendezéseket végrehajtó személyeket is. Ezt persze interpretálhatjuk úgyis, hogy ilyenkor magukra az egyéni preferenciarendezésekre mondunk ki állításokat, ami logikai szempontból azt jelenti, hogy másodrendű logikai konstrukciókat kell kezelnünk (☜) hiszen relációk (predikátumok) tulajdonságaira, kapcsolataira kell a kvantorainkat vonatkoztatni. Az első elemzett preferenciaprofil az egycsúcsú preferencia volt, amivel kapcsolatban fontos, ún. lehetségességi tételeket mondtak ki a társadalmi választások elméletén belül (☜) Ken-ichu Inada volt az, aki először tett kísérletet egy – bizonyos szemponból – kimerítőnek minősíthető preferenciaprofil-tipológia kidolgozására [Ken-i] [Ken-i] Inada 1969-es cikkében véglegesített tipológiáját befolyásolta Amartya K. Sen javaslata, amely eredményeként egy általánosabb kategória alá be lehetett sorolni Inada legfontosabb típusait, az ún. értékkorlátozott preferenciákat [Amart] [Amart] Inada profiltipológiáját később – egy új szempont figyelembe vételével – egy további típussal kibővítették, viszont az inadai típusok közül többeket elhagytak idővel, és inkább csak a Sen által is fókuszált értékkorlátozott profilokkal foglalkoztak alaposabban. Az egyes preferenciaprofilok ismertetésekor kezdetben igazodom Inada logikájához, de később eltérek az általa követett gondolatmenettől, és néhány típus bemutatását már más szerzők alapján végzem el.Inada preferenciaprofiljai
Ken-ichu Inada három olyan preferenciaprofilt mutatott be [Ken-i] amelyek tetszőleges számú szavazó esetén tranzitív közösségi preferenciát képesek adni az egyszerű többségi döntési eljárással. A preferenciaprofil-típusok leírásához Inada abból a kérdésből indult ki, hogy elméletileg milyen egyéni preferenciarendezések lehetségesek. Ha adva van három alternatívánk ($m,n,o$), akkor azokat tizenháromféleképpen lehet preferenciasorba állítani. Hatféleképpen rangsorolhatjuk őket úgy, hogy szigorú rendezést feltételezünk mindhárom alternatíva között, három-háromféle sorrend lehetséges akkor, ha egy alternatívát jobbnak, illetve rosszabbnak tartunk a másik kettő, egymással közömbös alternatívához képest, valamint egyféleképpen fordulhat elő az a helyzet, amikor mindhárom alternatíva közömbös egymással szemben. A szemléletesebb megjelenítés miatt kivételesen eltérve az eddigi gyakorlattól, a preferenciarelációk argumentumait infix-jelölésmódban kezelve, az alábbi táblázatban mutatom be a fent kifejtett lehetőségeket (csak a példa kedvéért jelzem, hogy az infix jelölésmód alkalmazásával a következő két formula ekvivalens egymással: $\rel{P}(m,n)\land \rel{P}(n,o) \equiv m \rel{P} n \rel{P} o$).| $m \rel{P} n \rel{P} o$ | $m \rel{P} n \rel{I} o$ | $ m \rel{I} n \rel{P} o$ | $m \rel{I} n \rel{I} o$ | |||||||||||
| $m \rel{P} o \rel{P} n$ | $n \rel{P} o \rel{I} m$ | $ n \rel{I} o \rel{P} m$ | ||||||||||||
| $n \rel{P} m \rel{P} o$ | $o \rel{P} m \rel{I} n$ | $ o \rel{I} m \rel{P} n$ | ||||||||||||
| $n \rel{P} o \rel{P} m$ | ||||||||||||||
| $o \rel{P} m \rel{P} n$ | ||||||||||||||
| $o \rel{P} n \rel{P} m$ | ||||||||||||||
$\concept{(DIP)} \defi \forall x \forall y \forall z \forall i(\lnot (\rel{P}_i(x,y) \land \rel{P}_i(y,z)))$
dichotóm (preferencia) (hun) – dichotomous preference (eng)
Inada kimondott egy tételt az ilyen preferenciaprofil esetére vonatkozóan, de ezt később mutatom majd be (☜) A következő preferenciaprofilokat már úgy kapjuk meg az inada építkezés során, hogy feltételezzük azt, hogy előfordulhatnak szigorú egyéni preferenciarendezések (vagyis a preferenciaminták között szerepelnek a fenti táblázat első oszlopából). Ez a feltétel önmagában azonban még nem szolgáltat érdekes mintázatot számunkra, további feltételeket kell megfogalmaznunk. Az egyik ilyen pluszfeltétel lehet, hogy kikötjük azt, hogy amikor fennáll egy adott szigorú hármas preferenciarendezés, akkor kizárjuk a rendezés két végén álló alternatíva közti fordított irányú szigorú rendezés létezését. A fenti táblázat alapján ez azt jelenti, hogy az első oszlop mintái közül megengedjük azokat, amelyek az egyik alternatíva (x) szigorúan jobb, mint a másik (z), de fordítva nem áll fent a kapcsolat köztük, vagyis az első három sorban levő típusok létezését engedjük csak meg. Inada ezt a típust nevezte el visszhangzó preferenciának. A kifejezéssel arra akart utalni, hogy ha van egy szavazó, aki tranzitív preferenciákkal rendelkezik, és a többiek is követik (visszhangozzák) őt ebben, akkor nyilvánvalóan teljesen a közösségi szavazat tranzitivitása is. Ezt a triviális esetet lehet általánosítani a most megfogalmazott feltétellel, amit a következő módon formalizálhatunk.$\concept{(ECP)} \defi \forall x \forall y \forall z \forall i(\rel{P}(x,y) \land \rel{P}_i(y,z)\to\lnot\rel{P}_i(z,x))$
visszhangzó (preferencia) (hun) – echoic preference (eng)
A következő preferenciaprofil felvezetéséhez Inada újracsak egy triviális példát hozott értelmezési mintául. Ha a szavazó közösség két diszjunkt csoportra osztható a szavazók "ízlése" szerint, azaz amíg az egyik csoport tagjai $x\rel{P}y\rel{P}z$ sorrend szerint szavaznak, addig a másik csoportba tartozók a $z\rel{P}y\rel{P}x$ mintát követik, akkor a többségi eljárás konzisztens közösségi végeredményt képes kihozni. Ezt a triviális esetet úgy lehet általánosítani, hogy amennyiben vannak, aki az $x\rel{P}y\rel{R}z$ sorrend szerint preferálják az alternatívákat, akkor vagy vannak olyanok is, akik a fordított rendezési sort preferálják ($z\rel{P}y\rel{R}x$), vagy vannak, akik a két szélső értéket tekintve közömbösek ($x\rel{I}z$). Ha ez így van, akkor – Inadát követve – antagonisztikus preferenciáról beszélhetünk, ami az alábbi formulával fejezhetünk ki.$\concept{(ANP)} \defi \forall x \forall y \forall z \forall i ((\rel{P}_i(x,y) \land \rel{P}_i(y,z)) \to (\rel{P}_i(z,y)\land \rel{P}_i(y,x)) \lor \rel{I}_i(x,z)) $
antagonisztikus (preferencia) (hun) – antagonistic preference (eng)
A dichotóm, a visszhangzó és az antagonisztikus preferenciaprofilok fogalmával szemben Inada úgy vezette be a tabu preferencia fogalmát, hogy jelezte, hogy utóbbi létezése esetén csak páratlan számú szavazó esetén remélhetünk konzisztens végeredményt a többségi eljárás alkalmazása során. A tabu preferencia lényege az, hogy egyfajta "preferenciaminta" nem fordulhat elő. Ezt azzal a kettős feltétellel vélte megragadhatónak Inada, hogy kizárta az alternatívák közti teljes közömbösség, valamint a kizárandó preferenciarendezés lehetőségét az egyéni preferenciarendezések köréből. Ezt az alábbi módon írhatjuk le.$\concept{(TAP)} \defi \forall x \forall y \forall z \forall i(\lnot (\rel{I}_i(x,y) \land \rel{I}_i(y,z)) \land \lnot \rel{P}_i(y,x))$
tabu (preferencia) (hun) – taboo preference (eng)
Az első három bemutatott inadai preferenciaprofil tetszőleges számú, a negyedjére elemzett mintázat csak páratlan számú szavazó esetén képes konzisztens végeredményt produkálni. Az első három, illetve a negyedik típus között elemezte Inada azokat a preferenciamintákat, amelyekre később Sen az értékkorlátozott minősítést alkalmazta. Mivel az idők során ezek a preferenciarendezések kerültek igazán az elemzői figyelem fókuszába, ezeket önállóan, a következő fejezetben mutatom be.Értékkorlátozott preferenciaprofilok
A legelőször vizsgálatba vont és azóta is a legtöbbet hivatkozott preferenciaprofil-típus az egycsúcsú preferencia. A fogalmat Duncan Black nevezte meg 1948-ban [Dunca] Arrow is hivatkozott rá 1951-es könyvében [Kenne] majd utánuk még sokan mások használták a kategóriát. Ha a szigorúan rendezett alternatívák halmazában van olyan elem, amely minden más elemhez képest jobbnak minősül, és a többi alternatíva értékelése (rendezése) speciális mintázat szerint, montonon módon csökkenve változik a maximális elemtől két irányban távolodva adott skálán mérve, akkor beszélünk egycsúcsú preferenciáról. Ekkor a lineárisan rendezett alternatívákra vonatkozóan a szavazók preferenciái vagy mindig szigorúan növekvő vagy szigorúan csökkenő vagy egy pontig először szigorúan növekvő, majd a ponttól szigorúan csökkenő függvényképet mutatnak. A fogalom értelmezéséhez segítséget jelenthet, ha bemutatok néhány példát az egycsúcsú preferenciákkal kapcsolatban. Az egyik példa hétköznapi. Ha egy nagy teremben több ágy van sorban egymás mellé rakva (mint egy laktanya körletében), és csak egy melegítőtest van, akkor minden egyes ágy birtokosának egycsúcsú a preferenciája, vagyis mindenki meg tudja mondani, hogy hol lenne számára a hőforrás ideális helye. Ez a hely természetesen mindenki esetében más és más pont lehet a teremben, ami részben a terem hossztengelye mentén elfoglalt pozíciótól, részben az ágytulajdonos "hőigényétől", "fázósságától" függ. Akik jobban szeretik a meleget, azok közelebb szeretnének a kályhához lenni, de lehet egy olyan pont, aminél közelebb már nem lenne annyira jó nekik, mert túlzottan sok meleg jönne rájuk. Ilyen helyzetben mindenki meg tudja valahogyan határozni azt, hogy neki mi lenne a hőforrás ideális elhelyezése, és az mindenki számára egycsúcsú preferencia elrendezést jelentene a lehetséges helyek halmazán. Gyakran hivatkoznak az egycsúcsú preferenciákra a közgazdaságtanban, illetve a politikai szociológia világában. Az érdeklődést Harold Hotelling híres cikke váltotta ki először [Hotel] amiben a szerző egy tengerparti sétányon vagy egy kisváros főutcáján működő boltok elhelyezkedéséről állított fel egy meglepő és igencsak "erős" tézist. Hotelling modellezte az a jólismert tényt, hogy amikor két konkurrens boltos helyet keres magának a város főutcáján (vagy az üdülőövezet sétányán), akkor mindketten a főutca (sétány) közepén fogják megnyitni a boltjukat. A magyarázat egyszerű. Ha feltételezzük, hogy a verseny miatt a boltosok minden minőségükben (árban, kínálatban, kiszolgálásban) megegyeznek, akkor a potenciális vevőknek csak az marad meg döntési szempontként, hogy melyik bolt van közelebb hozzájuk (a lakásukhoz, nyaralójukhoz). A Hotelling tétel szerint a boltosok akkor remélhetik a legnagyobb forgalmat, ha a lehető legtöbb vevőnek a lehető legkisebb sétálnivalója lesz, ezt pedig akkor érhetik el, ha valamennyien az utca, a sétány közepére települnek. A tétel azért érdekes számunkra, mert a magyarázat erősen támaszkodik az egycsúcsú preferencia létezésére (illetve annak tulajdonságaira). A szavazói preferenciák egycsúcsúságával magyarázzák a politikai pártok medián szavazókra optimalizáló viselkedését, és hasonló okok miatt kap fontos szerepet ez a fogalom a társadalmi választások elméletén belül a lehetségességi tételek között (☜) Az egycsúcsú preferenciák jellegzetessége az, hogy van egy maximális elem és a többi alternatíva ehhez képest egyre rosszabbnak minősül, bármelyik irányban is távolodunk a maximális elemtől. Ennek a speciális mintázatnak elképzelhetjük egyfajta tükörképét is, amikor van egy minimális elem, és minden más elem ehhez képes egyre jobbra értékelt, minél jobban távolodunk a minimális elemtől mindkét irányban. Az ilyen preferenciát Ken-ichi Inada egymélypontú preferenciának (vagy egyvölgyű preferenciának) nevezte el [Ken-i] Az egymélypontú preferencia fogalmával kifejezhetjük például a "közrosszhoz" való viszonyunkat. Amikor olyan döntést kell hozni, amit nem nagyon támogatnak az érintettek (hol épüljön a börtön, a menekülttábor, a hulladéktároló telep, a szemétfeldolgozó üzem stb.), akkor a preferenciáinkat nem a jobb, hanem inkább a rosszabb alternatívák szerint fejezzük ki. William Vickrey már Inada cikke előtt is utalt erre a preferenciatípusra, bár ő egymélypontú (single troughed) preferenciának nevezte el [Willi] Úgy tűnik, hogy az inadai 'single-caved' kifejezés helyett végül inkább a 'single-dipped' nyelvi szerkezet terjed el a szakirodalomban [Klaus] [Klaus] [Salva] Inada egy harmadik profiltípust is definiált, amit ugyanazzal a módszerrel határozott meg, mint amivel az egymélypontú preferencia fogalmát is "elválasztotta" az egycsúcsú preferencia fogalmától. Ekkor azonban a legnagyobb (legjobb) elem helyett nem a legkisebb (legrosszabb) elem cseréjét javasolta, hanem ehelyett inkább a hármas összehasonlítás harmadik elemére fókuszált az új fogalom definiálásakor. A szeparált preferenciának elnevezett új típus lényege az, hogy az alternatívák közül a szavazók mindig a két szélsőértéket hasonlítják össze vagyis minden esetben figyelmen kívül hagyják a "középső értéket". A három preferenciaprofilt a következőképpen definálhatjuk.$\concept{(SPP)} \defi \forall m\forall n\exists! o\forall i(((m< n \land n \le o) \to \rel{P}_i(n,m)) \land ((m>n \land n \ge o) \to \rel{P}_i(n,m)))$
egycsúcsú preferencia(profil) (hun) – egycsúcspontú preferencia(profil) (hun) – single-peaked preference (profile) (eng)
$\concept{(SDP)} \defi \forall m\forall n\exists! o\forall i(((m< n \land n \le o) \to \rel{P}_i(m,n)) \land ((m>n \land n \ge o) \to \rel{P}_i(m,n)))$
egymélypontú preferencia(profil) (hun) – egyvölgyű (hun) – egyvermű (hun) – single-caved (eng) – single-dipped preference (profile) (eng) – single troughed (eng)
$\concept{(GSP)} \defi \forall m \forall n \exists \mathbb{M}_1 \exists \mathbb{M}_2 \forall i(m \in \mathbb{M}_1 \land n \in \mathbb{M}_2 \land \mathbb{M}_1 \cap \mathbb{M}_2 = \emptyset \land \mathbb{M}_1 \cup \mathbb{M}_2 = \mathbb{X} \land \rel{R}_i(m,n) \lor \rel{R}_i(n,m))$
(szeparált preferencia) (hun) – (two-)group-separated preference (eng) – group-separable preference (eng)
Inada preferenciafogalmainak vagyis az egycsúcsú, az egymélypontú és a szeparált preferencia általánosításaként Amartya Sen javasolta használatba venni az értékkorlátozott preferencia (value-restricted preference) fogalmát [Amart] [Amart] Sen abból indult ki, amit már Inada is észrevett (sőt, ki is használt), hogy Arrow a lehetségességi tételeinek bizonyításakor (☜) valójában csak hármas összehasonlításokat tett, vagyis nem használta ki azt, hogy a tétel feltételei az összes alternatívára "egyszerre" vonatkoznak. Sen a három inadai preferenciatípust arra a közös vonásra hivatkozva vonta egy felettes kategória alá, hogy azok az alternatívák hármas összehasonlításakor mindig kizárják valamelyik elemet. Három elem ($m,n,o$) viszonylatában ki lehet hagyni a legrosszabb, a legjobb és a középső elemet, és ennek megfelelően beszélhetünk alsó-kizáró (worst-restricted), felső-kizáró (best-restricted) és közép-kizáró (medium-restricted) preferenciáról. Az egycsúcsú preferenciák Sen jellemzésében az alsó-kizáró típusba tartoznak, hiszen ebben az esetben nincsen legrosszabb elem egyik szavazó összehasonlításában sem. Az egyvölgyű preferenciáknak a felső-kizáró preferenciaprofil felel meg, hiszen senki preferenciarendezésében sem szerepel a legjobb elem. A szeparált preferencia esetében pedig közép-kizáróságról beszélhetünk, amikoris a középső alternatívát hagyja ki az összes szavazó a rendezéséből. Sen generikus alá-fölérendeltséget állapított meg az inadai típusok és saját értékkorlátozott preferenciaprofiljai között, de nem szabad elfeledkeznünk arról, hogy ez a kapcsolat "egyirányú". Ez azt jelenti, hogy minden egyvölgyű (egymélypontú, illetve szeparált) preferencia felső-kizáró (alsó-kizáró, illetve közép-kizáró) profilú, de a fordított kapcsolat nem áll fent. A kérdés az, hogy milyen további feltételekkel lehet egyértelműen meghatározni az inadai típusokat a Sen-féle értékkorlátozott mintázatokból. Miguel A. Ballester és Guillaume Haeringer erre a kérdésre adott választ további feltételek kidolgozásával [Balle] A szerzőpár egyfelől fölöslegesnek tartotta az alternatívák lineáris rendezését megkövetelő feltételt mondván, sok esetben nem lehet értelmesen interpretálni az alternatívák szigorú rendezettségét, másfelől bebizonyította, hogy két tulajdonság feltételezésével egyértelműen – és az alternatívák rendezettségére való hivatkozás nélkül – meghatározható az egycsúcsú (egymélypontú, szeparált) preferenciaprofil fogalma. Ballesterék szerint a Sen által bevezetett értékkorlátozott típusokra úgy tekinthetünk, mint amelyek szükséges feltételt jelentenek a három inadai profil definiálásához. Az elégséges feltételhez a szerzők új tulajdonságokat ($\alpha, \alpha^{- 1}, \beta$) definiáltak. Az $\alpha$-tulajdonság akkor érvényesül, ha két szavazónak három alternatívára vonatkozóan teljesen ellentétes a preferenciarendezése, de egy negyedik alternatívát mindketten jobbnak tartanak a hármas alternatívasor középső eleménél. Az inverz $\alpha$-tulajdonság csak annyiban különbözik ettől, hogy a negyedik alternatívát rosszabbnak tartja mindkettő szavazó a hármas sor középső eleménél. A $\beta$-tulajdonsággal azt az helyzetet írhatjuk le, amelyben egyrészt két tetszőleges szavazó által legrosszabbnak, illetve legjobbnak tartott alternatívák különböznek egymástól, másrészt amíg az egyik szavazó két szélsőértékének sorrendjében megegyeznek a szavazók, addig a másik szavazó két szélsőértékének sorrendjében eltérően értékelik. A tulajdonságok formulái a következők. [♦]$\alpha\concept{-RESTRICTED} \defi \exists m \exists n \exists o \exists r \exists i \exists j((m \rel{P}_i n \rel{P}_i o \land n \rel{P}_i r) \land (o \rel{P}_j n \rel{P}_j m \land n \rel{P}_j r))$
$\alpha$-tulajdonság (hun) – $\alpha$-property (eng)
$\alpha^{- 1}\concept{-RESTRICTED} \defi \exists m \exists n \exists o \exists r \exists i \exists j((m \rel{P}_i n \rel{P}_i o \land r \rel{P}_i n) \land (o \rel{P}_j n \rel{P}_j m \land r \rel{P}_j n))$
inverz $\alpha$-tulajdonság (hun) – converse $\alpha$-property (eng)
$\beta\concept{-RESTRICTED} \defi \exists m \exists n \exists o \exists r \exists i \exists j((m \rel{P}_i n \rel{P}_i o \rel{P}_i r) \land (n \rel{P}_j r \rel{P}_j m \rel{P}_j o))$
$\beta$-tulajdonság (hun) – $\beta$-property (eng)
Mindhárom tulajdonságot összekapcsolhatjuk valamelyik érték-korlátozott preferenciaprofillal, de ezt tagadó módon tehetjük meg. Ha ugyanis azt tapasztaljuk, hogy valamelyik tulajdonság igaz egy "ismeretlen" preferenciaprofilra nézve, akkor mondhatjuk, hogy ez a profil nem tartozhat abba a típusba, amit hozzárendeltük a szóban forgó tulajdonságot. Ez azt is jelenti egyben, hogy az inadai három preferenciaprofil-típusát definiálhatjuk úgy is, hogy a meghatározásaikba belevesszük a velük összekapcsolt tulajdonságok tagadását.$\concept{(SSP)} \equiv\concept{SINGLE-PEAKED} \leftrightarrow \concept{WORST-RESTRICTED} \;\land \neg \alpha\concept{-RESTRICTED}$
Ballester-Haeringer egycsúcsú preferencia tétele (hun) – Ballester-Haeringer's theorem on single-peaked preference profile (eng)
$\concept{(SDP)} \equiv\concept{SINGLE-DIPPED} \leftrightarrow \concept{BEST-RESTRICTED} \;\land \neg \alpha^{- 1}\concept{-RESTRICTED}$
Ballester-Haeringer egymélypontú preferencia tétele (hun) – Ballester-Haeringer's theorem on single-dipped preference profile (eng)
$\concept{(GSP)} \equiv\concept{GROUP-SEPARATED} \leftrightarrow \concept{MEDIUM-RESTRICTED} \; \land \neg \beta\concept{-RESTRICTED} $
Ballester-Haeringer szeparált preferencia tétele (hun) – Ballester-Haeringer's theorem on group-separated preference profile (eng)
Ezzel az újraértelmezéssel könnyebben felismerhetjük az egycsúcsúság (egymélypontúság, szeparáltság) tulajdonságát, amikor egy "ismeretlen" preferenciaprofilt reprezentáló adatokra tekintünk [Aleja] Az alábbi két példára nézve "könnyen" megállapíthatjuk, hogy az első táblázat nem elégíti ki az egycsúcsúság feltételét, hiszen mindhárom alternatíva szerepel a legrosszabb helyen valamelyik egyéni preferenciarendezésben. Ezzel szemben a második tábla adatai alapján ráismerhetünk az egycsúcsú preferenciaprofilra, ha észrevesszük, hogy van olyan elem (n), amely sosincs a legrosszabb pozícióban a hármas összehasonlítások során (praktikusan ez azt jelenti, hogy a 2. példa adatait "oszlopszerűen" nézve az alternatívák utolsó két oszlopában nem fordul elő az n alternatíva).| 1. példa | 2. példa | |||||||||||||
| $m \rel{P}_1 n \rel{P}_1 o$ | $m \rel{P}_1 n \rel{P}_1 o \rel{P}_1 r$ | |||||||||||||
| $m \rel{P}_2 o \rel{P}_2 n$ | $o \rel{P}_2 n \rel{P}_2 m \rel{P}_2 r$ | |||||||||||||
| $o \rel{P}_3 n \rel{P}_3 m$ | $n \rel{P}_3 m \rel{P}_3 r \rel{P}_3 o$ | |||||||||||||
Az ábrákra tekintve egyből látható a kétféle preferencia különbsége, az, ahogy a csúcsosság felfelé vagy lefelé érvényesül – az előbbi az egycsúcsú, az utóbbi az egymélypontú preferenciák esetében. Ha a harmadik inadai típust is ábrázolni akarjuk, akkor ahhoz az alábbi adatokból érdemes kiindulnunk.
| $\rel{Q}_1 = m \rel{I} n \rel{P} r \rel{P} o$ | ||||||||||||||
| $\rel{Q}_2 = m \rel{P} n \rel{P} o \rel{P} r$ | ||||||||||||||
| $\rel{Q}_3 = n \rel{P} m \rel{P} o \rel{I} r$ | ||||||||||||||
| $\rel{Q}_4 = r \rel{P} o \rel{P} m \rel{P} n$ | ||||||||||||||
| $\rel{Q}_5 = o \rel{P} r \rel{P} n \rel{P} m$ | ||||||||||||||
| $\rel{Q}_6 = o \rel{I} r \rel{P} m \rel{I} n$ | ||||||||||||||
A második és harmadik grafikonon jól látszik, hogy az ott látható három-három görbe hasonló egyéni preferenciaprofilokat takar. A $Q_1, Q_2, Q_3$ esetben az m és n alternatívák mindig többre vannak értékelve a másik kettőnél, a $Q_4, Q_5, Q_6$ esetben ez pont fordítva van, és az o és r alternatívákat mindig jobbnak tartják az m-nél vagy n-nél. A szeparált preferenciaprofil további fontos vonása még (ami persze itt nem látszik), hogy bináris gráffal lehet reprezentálni [Ken-i]
Egyszerváltó preferencia
A preferenciaprofilokról szóló diskurzusba az inadai típusok mellé a hetvenes-nyolcvanas évektől kezdve bekerült még egy további mintázat, az egyszerváltó preferencia (single-crossing preference) profiltípusa is. A fogalommal kapcsolatos példaként gyakran hivatkoznak az adózási kulcsokra vonatkozó szavazások jelenségére. Kevin W.S. Roberts volt az, aki elsőként leírta ezt a jelenséget, bár ő még más terminust használt rá, amikor bevezette a hierarchikus tapadás feltétel (hierarchical adherence condition) fogalmát [Kevin] Egyszerváltó preferenciáról akkor beszélhetünk, amikor nemcsak az alternatívák halmaza, de a szavazók halmaza is lineáris sorba rendezhető. Gondolhatunk itt arra a helyzetre, amikor az adókulcsok mértékről kell szavazni, és eközben maguk a szavazók egyértelműen sorba rendezhetők a jövedelmi-vagyoni helyzetük szerint. Ilyen esetben megtapasztalhatjuk az egyszerváltó preferencia jelenségét, ami azt jelenti, hogy az embereket a jövedelem (vagyon) alapján szigorú sorba rendezve észrevehetjük, hogy amíg a gazdagabbak kisebb adókulcsokat szeretnének, addig a szegényebbek magasabb (és progresszív) adókulcsokra szavaznának. Ez érthető is, hiszen az adózás értelme – ebből a szempontból tekintve – éppen az, hogy a magasabb jövedelműek rétege felől áramoltassanak át erőforrásokat az alacsonyabb jövedelműek rétegei felé. Ebben a helyzetben az egyszerváltó tulajdonság azt jelenti, hogy az egyéni preferenciákra vonatkozóan – elég egyértelműen – kijelenthetjük, hogy a "szegényebb" pólus felől indulva sokáig a magasabb kulcsokat támogatják a szavazók, a másik irány felől indulva visszafelé sokáig az alacsonyabb kulcsokat preferálják, és az is elképzelhető, hogy valahol a két pólus között van egy olyan átmeneti réteg, amely indifferens ebben a kérdésben, de az is előfordulhat, hogy nincs ilyen halmaz, és ilyenkor létezik egy pont, ahol az egyéni preferenciák "előjelet", értéket váltanak. Ez az egyszeri trendváltás az egyszerváltó preferenciaprofil lényege. A pár oldallal korábban bemutatott kettős példára hivatkozva azt mondhatjuk, hogy az első példa nemcsak az egymélypontú, de az egyszerváltó preferenciára is vonatkoztatható lenne. Ahogy Miguel A. Ballester és Guillaume Haeringe megmutatta azt, hogy milyen feltételekkel lehet Inada és Sen profiltípusai között egyértelmű megfeleltetést találni, úgy Robert Bredereck, Jiehua Chen és Gerhard J. Woeginger elvégezte azt a munkát az egyszerváltó preferenciák esetében is [Rober]
$\concept{(SCP)} \defi \forall m \forall n \forall i\forall j(({n}>{m} \land \rel{P}_j \succ \rel{P}_i \land \rel{P}_i(n,m))\to \rel{P}_j(n,m)) \land $
$\forall m \forall n \forall i\forall j(({n}>{m} \land \rel{P}_j \succ \rel{P}_i \land \rel{P}_j(m,n))\to \rel{P}_i(m,n))$
egyszerváltó preferencia (hun) – single-crossing preference (eng)
Ennek a preferenciatípusnak komoly szerepe van a reprezentatív szavazó elméletében, és lehetségességi tételek is megfogalmazhatók vele kapcsolatban. A most tárgyalt kategóriák alapján meg lehetne próbálkozni a fogalmak valamiféle általánosításával, de erre a feladatra én nem vállalkozom. Ilyen kísérletek természetesen vannak, Salvador Barber\'{a} és Bernardo Moreno például a topmonotonitás kategóriáját az egycsúcsú és az egyszerváltó preferenciák fölérendelt fogalmaként javasolta alkalmazni [Barbe] de az effajta absztrakciónak egyelőre nem látom az igazi hozadékát.Preferenciaaggregálás
A preferenciáról szóló fejezetben bemutattam, hogy e jelenségről szólva mindig négyféle preferencia-vonatkozású relációt kell figyelembe vennünk (☜) A társadalmi választások elméletében - csakúgy, mint más preferencia-vonatkozűsú elméletekben – elsősorban a gyenge preferenciarendezés (☜) és az erős preferenciarendezés (☜) fogalmait használják, de olykor-olykor felbukkan a preferenciarelációk körébe sorolható közömbösség (☜) illetve az összehasonlíthatatlanság (☜) relációja is. Mielőtt a preferenciaggregálás sajátosságainak tárgyalásába kezdenék, röviden felvázolok egy olyan értelmezési keretet, amely végig segítségemre lehet a jelenségek bemutatásában azáltal, hogy összeköti az egyes elemzendő kérdésköröket.Manipuláció
A társadalmi választások elméletén belül a szavazás jelenségének talán legfontosabb vonása a manipuláció lehetősége. Az egyéni preferenciák aggregálása egyetlen közösségi véleménnyé nem kizárólag az egyéni véleményektől függ, hanem sok minden mástól, és ezeket mind – valamilyen szinten – meg lehet változtatni, amivel a végeredményt is lehet befolyásolni. A manipulációnak sok értelme, sok formája, sokféle "színtere" lehetséges. A társadalmi választások elméletében legelterjedtebb manipulációértelmezés az egyéni preferenciák kinyilvánításával, a leadott szavazatok őszinteségével kapcsolatos (☜) A stratégiai szavazásnak nevezett jelenség a szavazók által direkt módon megvalósított szavazatmanipulációt jelenti, amikor a saját egyéni preferenciarendezésüket megváltoztatják a szavazatgazdák vagyis a szavazók. Ezzel szemben áll az az indirekt szavazatmanipuláció, amikor ugyanúgy az egyéni preferenciarendezések változnak meg, de itt nem a szavazók maguk változtatják meg tudatosan saját véleményüket, hanem mások hatására, a külső véleménybefolyásolások eredményeként lesz más a vélemény. Ekkor a szavazók őszintén szavaznak, szemben a stratégiai szavazás őszintétlenségével. A külsődleges véleménybefolyásolás hatására bekövetkező véleményváltoztatás jeelnségét azonban, bár fontossága nem kérdőjelezhető meg, itt mégsem vizsgálom, mivel ez más tudományterület elemzési körébe tartozik. Másfajta manipulációról beszélhetünk akkor, amikor az alternatívák halmaza változik meg valamiért. Az nagyon fontos kérdés, hogy miért is változ(hat)nak meg az értékelendő alternatívák. A dolgokat itt is leegyszerűsítve azt mondhatjuk, hogy szavazási kontextusban az alternatívák maguktól, a szavazók felől tekintve nem változnak meg. Ha változik valami e téren, akkor mindez azoknak a hatására történik, akik felelnek a szavazásért, akik kontroll alatt tartják a választási folyamatot. Ha ezeket elnevezzük aggregációgazdáknak, akkor azt mondhatjuk, hogy az alternatívamanipuláció, amikor az alternatívák, a jelöltek listáját megváltoztatják az aggregációgazdák, kívül esik az aggregációs folyamatok logikáján. Ez a kérdés a választás normatív kontextusában elemezhető, ezért ennek tárgyalását is elhagyom. Fontos kérdés, de nem az aggregálás jelenségébe tartozik. Hasonlókat mondhatunk a szavazójog-manipuláció kérdéséről is. A szavazások, választások végeredményét befolyásolja az a tény, hogy kik a szavazók, kiknek a véleménye számít. Ez is fontos történelmi, társadalmi kérdés, gondoljunk csak a nők választójogának megjelenésére, a cenzus alapú választójog eltűnésére, a 'ki a szabad', 'ki a felnőtt' kérdésekre adott válaszok történetére, a szavazati jog megvonása mint egyéni vagy kollektív büntetés jelenségére, vagy a Magyarország határain kívül élő magyarok, magyar állampolgárok szavazati jogának kezelésére. Ebben a jelenségben is van manipulációs potenciál, ez is a választáshoz tartozik, de ezt sem elemzem itt. Ugyanazért nem, mint ahogy a korábbi témaköröket is elhagytam: más tudományterület relevanciájába tartozik. Van azonban két olyan manipulációs lehetőség a választásokkal kapcsolatban, amit végre már "elemezhetek". Az egyik az algoritmusmanipuláció, [♦] amikor az aggregálási eljárást megváltoztatják az aggregációgazdák, hogy ezzel befolyásolják a végeredményt, a másik a körzethatár-manipuláció, amikor a körzethatárokat változatják meg politikai, gazdasági előnyök reményében. Az első kérdéskört a következő fejezetekben alaposabban körbe járom, a második problémát csak röviden említem (☜) [♦]Algoritmusmanipuláció
Azt, hogy a szavazási eljárás választása önmagában befolyásolhatja a csoportszavazás végeredményét, már legalább a rómaiak óta tudjuk. Nem lehet nem megidézni azt a mesét, amiről ifjabb Plinius egyik levelében számolt be [Ifjab] és ami a társadalmi választások elméletének talán leggyakrabban idézett példájává vált [Robin] [Willi] [Peter] A történetet Plinius eredeti meséjéhez képest kicsit megváltoztatva mutatom be, hogy szemléletesebb, karakteresebb legyen a tanulsága. Ifjabb Plinius beszámolója szerint Afranius Dexter szenátor holtan találják a villájában, és a gyanú a felszabadított rabszolgáira terelődik. Tegyük fel, hogy a szenátorok egy 12 tagú csoportjának kell meghoznia kell a végső döntést, akik három alternatíva közül választhatnak.| $F$ | felmentés | |||||||||||||
| $K$ | kivégzés | |||||||||||||
| $S$ | száműzés | |||||||||||||
| 1. csoport | $FSK$ | 5 | ||||||||||||
| 2. csoport | $KSF$ | 4 | ||||||||||||
| 3. csoport | $SFK$ | 3 | ||||||||||||
| $F$ | 5 szavazat | az 1. csoport mindegyik tagja ide szavaz | ||||||||||||
| $B$ | 3 szavazat | a 3. csoport mindegyik tagja ide szavaz | ||||||||||||
| $K$ | 4 szavazat | a 2. csoport mindegyik tagja ide szavaz | ||||||||||||
| bűnös: | 4+3 szavazat | a 2. és 3. csoport tagjai ide szavaznak | ||||||||||||
| nem bűnös: | 5 szavazat | az 1. csoport mindegyik tagja ide szavaz | ||||||||||||
| $K$ | 4 szavazat | a 2. csoport mindegyik tagja ide szavaz | ||||||||||||
| $B$ | 3+5 szavazat | a 3. csoport az elsődleges preferenciája, míg az 1. csoport a másodlagos preferenciája szerint szavaz ide | ||||||||||||
| 1. szavazó | $x y b a$ | |||||||||||||
| 2. szavazó | $a x y b$ | |||||||||||||
| 3. szavazó | $b a x y$ | |||||||||||||
| 1. | 2. | 3. | 4. | 5. | 6. | 7. | alternatíva | Borda-pont | ||||||
| $a$ | $b$ | $c$ | $a$ | $b$ | $c$ | $a$ | $a$ | $18 = (3\times 4) + (2\times 2) + (2\times 1)$ | ||||||
| $b$ | $c$ | $x$ | $b$ | $c$ | $x$ | $b$ | $b$ | $19 = (2\times 4) + (3\times 3) + (2 \times 1)$ | ||||||
| $c$ | $x$ | $a$ | $c$ | $x$ | $a$ | $c$ | $c$ | $20 = (2\times 4) + (2\times 3) + (3\times 2)$ | ||||||
| $x$ | $a$ | $b$ | $x$ | $a$ | $b$ | $x$ | $x$ | $13 = (2\times 3) + (2\times 2) + (3\times 1)$ | ||||||
| 1. | 2. | 3. | 4. | 5. | 6. | 7. | alternatíva | Borda-pont | ||||||
| $a$ | $b$ | $c$ | $a$ | $b$ | $c$ | $a$ | $a$ | $15 = (3\times 3) + (2\times 2) + (2\times 1)$ | ||||||
| $b$ | $c$ | $a$ | $b$ | $c$ | $a$ | $b$ | $b$ | $14 = (2\times 3) + (3\times 2) + (2 \times 1)$ | ||||||
| $c$ | $a$ | $b$ | $c$ | $a$ | $b$ | $c$ | $c$ | $13 = (2\times 3) + (2\times 2) + (3\times 1)$ | ||||||
| MSZP | SZDSZ | MDF | FKGP | FIDESZ | KDNP | |||||||||
| legnagyobb maradék módszere | 54,1 | 17,9 | 9,8 | 6,7 | 5,2 | 5,7 | ||||||||
| Imperiali módszer | 55,4 | 17,9 | 9,6 | 6,7 | 4,7 | 5,2 | ||||||||
| d'Hondt módszer | 57,5 | 19,4 | 9,1 | 6,0 | 3,3 | 4,1 | ||||||||
| Hagenbach-Bischoff módszer | 54,9 | 17,1 | 9,6 | 7,0 | 5,2 | 5,7 | ||||||||
| Sainte-Laguë módszer (osztó: 1) | 53,9 | 17,1 | 10,4 | 7,0 | 5,2 | 6,0 | ||||||||
| Sainte-Laguë módszer (osztó: 1,4) | 55,7 | 18,4 | 9,8 | 5,2 | 4,4 | 4,9 | ||||||||
| Sainte-Laguë módszer (osztó: 1,2) | 54,1 | 17,9 | 9,8 | 6,7 | 5,2 | 5,7 | ||||||||
Condorcet-paradoxon
Nicolas de Condorcet francia matematikus és filozófus már a 18. században leírta azt a paradoxont, amit később róla neveztek el. Legalább Condorcet óta tudjuk tehát, hogy amikor az egyéni preferenciák alapján egy közösségi sorrendet kell kialakítani valamilyen alternatívahalmazon, akkor a többségi eljárással nem remélhetünk minden esetben végeredményt. A Condorcet-féle módszer a Condorcet-győztes elemet úgy hozza ki, hogy az egyéni rendezések alapján összehasonlítja az összes alternatívát egymással, és a páros összehasonlítások részeredményeit összesítve a többségi elv alapján hirdeti ki a győztest. A Condorcet-paradoxon lényege az, hogy könnyen preferenciakör, tranzitív kör alakulhat ki az ilyen eljárás során. A körkörös többség jelenségét szemléltethetjük az alábbi táblázat segítségével (szigorú preferenciarendezést feltételezve).| feltétel | következmény | |||||||||||||
| 1. egyéni vélemény | $\rel{P}(m,n) \land \rel{P}(n,o)$ | $\rel{P}(m,o)$ | ||||||||||||
| 2. egyéni vélemény | $\rel{P}(n,o) \land \rel{P}(o,m)$ | $\rel{P}(n,m)$ | ||||||||||||
| 3. egyéni vélemény | $\rel{P}(o,m) \land \rel{P}(m,n)$ | $\rel{P}(o,n)$ | ||||||||||||
| többségi vélemény | $\rel{P}(m,n)\land \rel{P}(n,o) \land \rel{P}(o,m)$ | $?$ | ||||||||||||
Arrow lehetetlenségi tétele
Nem nagyon vitatkoznék azzal, ha valaki azt állítaná, hogy a preferenciaaggregálás egész világa Kenneth J. Arrow lehetetlenségi tétele körül forog. Arrow 1950 fogalmazta meg először híres tételét [K.J.A] majd 1951-ben egy kis könyvet jelentetett meg ugyanerről a kérdésről [Kenne] [♦] Az egyéni preferenciákat aggregáló függvényt társadalmi jóléti függvénynek (social welfare function) nevezve, az aggregálási folyamatra vonatkozóan különböző elvárásokat megfogalmazva, Arrow kimondott egy tételt, miszerint azok az elvárások, amelyeket elég széles körű egyetértés alapján a véleményösszegzési eljárásokkal szemben támasztunk, nem elégíthetők ki egyszerre. Vegyük sorba egymás után, milyen elvárásaink lehetnek az összegző függvénnyel szemben. [♦] Nyilván meg kell követelnünk az aggregálási szabálytól azt, hogy mindenféle konstellációban képes legyen eredményt produkálni – akárhogyan is alakulnak az alternatívák és az egyéni preferenciarendezések. Ez az elvárás azonban kétféle dolgot is jelent, ami alapján a bemenetre és a kimenetre is megfogalmazhatunk egy-egy részfeltételt. A bemenetre vonatkozó feltételünk az lehet, hogy mindenféle bemenetet be tudjon fogadni a rendszer, ebben az értelemben legyen egyetemes, univerzális. A kimenetre vonatkozóan pedig azt az elvárást rögzíthetjük, hogy egyetlen, tehát egyértelmű végeredményt adjon ki a rendszer az összesítés után. Az persze előfordulhat – szinte bármelyik aggregáló szabály esetében –, hogy a szavazatok összegzése döntetlent eredményez. Ilyenkor szükség lehet egy másodlagos döntetlentörő szabályra (tie-break rule), ami segít a döntetlent megszüntetni. Ez azonban a főszabályra vonatkozó elvárásunkat nem érinti lényegi módon. A két tulajdonság, amit a fentiek alapján definiálhatunk a következő.$\concept{(UNI)}\equiv\concept{UNIVERSAL}(\rel{F})\defi \mathbb{D}_F = \mathbb{X}^n$
univerzális (értelmezési tartomány) (hun) – korlátozatlan értelmezési tartomány (hun) – universal (domain) (eng) – unrestricted domain (eng)
$\concept{(DEC)}\equiv\concept{DECISIVE}(\rel{F})\defi \forall a (|\rel{F}(a) |= 1)$
döntésképes (hun) – (ügy)döntő (hun) – decisive (eng)
Az első követelmény az univerzalitás tulajdonsága, ami tehát azt jelenti, hogy az összegző függvény értelmezve van minden lehetséges bemenetre. Matematikailag ezt úgy ragadhatjuk meg, hogy az $\rel{F}$ aggregáló függvény $\mathbb{D}_F$ értelmezési tartományát egyenlővé tesszük a teljes állapotteret jelző $\mathbb{X}^n$ halmazzal. Az univerzalitás felétele azt jelenti tartalmilag, hogy az aggregáló függvénytől elvárjuk azt, hogy bármilyen (bárki által megfogalmazott) lehetséges preferenciarendezést figyelembe vegyen a közösségi vélemény kialakításakor, ami egyet jelent azzal, hogy az egyének szabadon alakíthassák ki saját egyéni sorrendjeiket a világ dolgait illetően. Ez az elv tehát az szabad véleménykinyilvánítás egy fontos esetét írja le. Ha elhagyjuk az univerzalitás követelményét, akkor valamilyen módon korlátozott tartományról kell beszélnünk. Erre példa az egycsúcsú preferenciák esete (☜) amelyre vonatkozóan Duncan Black fontos tétel fogalmazott meg, amit később fogok bemutatni (☜) Bár a jelenség lényegét tekintve nem ide tartozik, de azért érdemes megjegyeznem, hogy amikor a diktatórikus rendszerek megakadályozzák, hogy a szavazáson tetszőleges jelöltek indulhassanak, akkor voltaképpen az itt tárgyalt univerzalitási kritériumnak nem tesznek eleget. Amíg az első elvárás a függvény bemenetére rögzített egy kritériumot, addig az aggregáló függvény döntésképes jellegére irányuló feltétel a függvény kimenetére irányul. A fentebb már jelzett elvárás, miszerint az összegző eljárásnak minden lehetséges bemenetre egyértelmű végeredményt kell adnia, azt a szimpla és nagyon praktikus elvet akarja érvényesíteni, hogy értelme legyen az aggregálási eljárás lefolytatásának. Arra ugyanis pont azért van szükség, mert a sok egyéni vélemény nem egyezik meg egymással, tehát nincs konszenzus az egyéni szinten, az érintettek nem tudnak kollektíve dönteni. Ilyen helyzetekben azért kell az aggregálási eljárást elindítani, hogy legyen kollektív döntés. De csak akkor beszélhetünk döntésről, ha egyetlen kimenetünk van. Ez biztosítja az eljárás döntésképes tulajdonsága. A lehetetlenségi tétel első megfogalmazásakor Arrow még öt tulajdonságot különített el egymástól [K.J.A] és csak később alakította át úgy az elméletét, hogy négy tulajdonságról legyen szó. A tétel első megfogalmazásában még szerepelt a monotonitás fogalma is, amit a relációelméleti fejezetben mi már definiáltunk, mint fontos függvénytulajdonságot (☜) A monotonitás kritériumát itt nyilván az $\rel{F}$ összegzőfüggvényre kell vonatkoztatnunk.$\concept{(MON)}\equiv\concept{MONOTONE}(\rel{F})\defi \forall a \forall b \forall m((\rel{F} (\langle \rel{R}^a_i \rangle_{i \in \mathbb{N}})=m \land (\rel{R}^a_i=m \to \rel{R}_i^{b}=m))\to \rel{F} (\langle \rel{R}_i^{b} \rangle_{i \in \mathbb{N}})=m)$
monoton (hun) – monotone (eng)
Arrow ezt az egyéni és csoportos értékek közti pozitív kapcsolat (positive association of social and individual values) elvárásaként is értelmezi [K.J.A] Ha az egyéni rendezésekben az egyik alternatíva mindig egy másik előtt szerepel, akkor ugyanennek a rendezésnek kell megjelennie a kollektív preferencia szintjén is. A monotonitás helyett azonban nagyon hamar egy másik tulajdonság került be a lehetetlenségi tétel(ek)ről folytatott diskurzusba, az irreleváns alternatíváktól való függetlenség elvárása. [♦] (☜) A fogalom értelmezését kezdhetjük azzal, amit Arrow maga mondott erről. [♦]"Az ordinális hasznossághoz való újkeletű ragaszkodást a megkülönböztethetetlenek azonosságának leibniz-i elvével magyarázhatjuk. Csak a megfigyelhető különbségeket tehetjük meg a magyarázataink alapjául. … Az Irreleváns Alternatívák Függetlenségének Feltétele egy lépéssel tovább megy a megfigyelhetőség követelményén. Ha adott a társadalom számára választható alternatívák halmaza, akkor – elméletileg – elvárható, hogy valaki képes lehet az összes alternatíva mérlegelésére, de nem várhatjuk el azt, hogy figyelembe vegyen a társadalom számára nem elérhető (nem létező) alternatívák közti preferenciákat." [Kenne]
Azt az elvárást kell itt megfogalmazni valahogyan, hogy a közösségi preferenciarendezések eredményei csak az összehasonlításba bevont alternatívákra vonatkozó egyéni preferenciáktól függjenek, semmi mástól. Ha az egyéni preferenciák két alternatíva között nem változtak, de – esetleg – más alternatívák között igen, akkor a közösségi preferencia sem változhat a szóbanforgó alternatívákra.$\concept{(IIA)}\equiv\concept{IIA}(\rel{F})\defi\forall i \forall a \forall b \forall m \forall n((\rel{R}_i^a(m,n) \leftrightarrow \rel{R}_i^{b}(m,n))\to (\rel{F}(a)(m,n)\leftrightarrow \rel{F}(b)(m,n)))$
független az irreleváns altenatíváktól (hun) – independent from the irrelevant alternatives (eng) – binary independence (eng)
Az elv szemléltetésére nézzünk meg egy egyszerű példát. Tegyük fel, hogy van három szavazónk, $v_1, v_2$ és $v_3$, valmint négy alternatívánk, $m, n, o$ és p. A következő táblázatban tüntessük fel azt, hogy a szavazók hogyan rangsorolják az alternatívákat, illetve milyen sorrendet hoz ki az $\rel{F}$ szavazási függvény két alternatíva, m és n között. Az irreleváns alternatívák függetlensége azt jelenti, hogy ha az első sorban feltüntetett egyéni rendezésekből az összegző függvény a m alternatívát hozza ki a n elé, akkor minden más profilegyüttesre is tartania kell ezt a sorrendet.| $v_1$ szavazó | $v_2$ szavazó | $v_3$ szavazó | $\rel{F}$ | |||||||||||
| $(m,n,o,p)$ | $(n,p,o,m)$ | $(o,m,p,n)$ | $m > n)$ | |||||||||||
| $(m,o,p,n)$ | $(o,n,p,m)$ | $(m,n,o,p)$ | $m > n)$ | jó | ||||||||||
| $(p,m,n,o)$ | $(n,m,o,p)$ | $(o,p,m,n)$ | $m > n)$ | jó | ||||||||||
| $(n,p,o,m)$ | $(o,p,n,m)$ | $(p,m,o,n)$ | $m > n)$ | rossz | ||||||||||
| $(m,n,o,p)$ | $(n,p,o,m)$ | $(o,m,p,n)$ | $m < n)$ | rossz | ||||||||||
$\concept{(WPE)}\equiv\concept{WEAKLY\_PARETO\_EFFICIENT}(\rel{F})\defi \forall a \forall m \forall n((a=(\rel{R}_1^a, \rel{R}_2^a, \dots, \rel{R}_{|\mathbb{N}|}^a)\land (m,n)\in \mathbb{X} \land C^a=\rel{F}(a))$
$\to ((m,n)\in \bigcap\limits_{i \in \mathbb{N}} \rel{P}(\rel{R}_i^a) \to (m \in C^a(\{m,n\}))))$
gyengén Pareto hatékony (hun) – weakly Pareto efficient (eng) – gyengén Pareto optimális (hun) – weakly Pareto optimal (eng) – wPo (eng)
$\concept{(PE)}\equiv\concept{PARETO\_EFFICIENT}(\rel{F})\defi \forall a \forall m \forall n((a=(\rel{R}_1^a, \rel{R}_2^a, \dots, \rel{R}_{|\mathbb{N}|}^a)\land (m,n)\in \mathbb{X})\to ((m,n)\in \bigcap\limits_{i \in \mathbb{N}} \rel{P}(\rel{R}_i^a) $
$\to (m \in S \to n \notin C^a(S))))$
Pareto hatékony (hun) – Pareto efficient (eng) – Pareto optimális (hun) – Pareto optimal (eng) – Po (eng)
$\concept{(SPE)}\equiv\concept{STRONGLY\_PARETO\_EFFICIENT}(\rel{F})\defi \forall a \forall m \forall n((a=(\rel{R}_1^a, \rel{R}_2^a, \dots, \rel{R}_{|\mathbb{N}|}^a)\land (m,n)\in \mathbb{X}\land C^a=\rel{F}(a))$
$\to ((m,n)\in \bigcap\limits_{i \in \mathbb{N}} \rel{P}(\rel{R}_i^a) \to (m \in S \to n \notin C^a(S))))$
erősen Pareto hatékony (hun) – strongly Pareto efficient (eng) – erősen Pareto optimális (hun) – strongly Pareto optimal (eng) – sPo (eng)
A Pareto-feltételeket egyfajta egyhangúságnak, egyöntetűségnek minősíthetjük, aminek az a lényege, hogy ha az m alternatívát minden szavazó prefereálja az n-nel szemben, akkor n nem lehet győztes. Fontos azonban jelezni, hogy ha az egyöntetűséget mint a konszenzus elvének megvalósítását értelmezzük, vagyis a szavazás egyhangúságával a teljes konszenzust várjuk el, akkor a szavazók a szavazás során könnyen stratégiai szavazókká válhatnak, és elkezdhetik "működtetni" a szavazatcsere intézményét (☜) Az is fontos elvárás lehet a választási függvénnyel szemben, hogy ne egyetlen személy (vagy csoport) véleménye érvényesüljön az aggregálás során, vagyis azt várjuk el, hogy mindenki véleménye számítson az összegzés során, és ne fordulhassanak elő oligarchikus vagy diktatórikus megoldások. Ha arra a szempontra figyelünk, hogy milyen az egyéni és csoportos vélemények közti viszony, kétféle tulajdonságot is definiálhatunk, a kikényszerítettséget és a diktatórikusságot (illetve ezek komplementerét). Ezeket akkor érthetjük meg jól, ha előtte még más fogalmakat is bevezetünk a modellünkbe. Először képeznünk kell a szavazók tetszőleges csoportját, koalícióját, amelyek közül kiemeljük majd azokat, amelyeknek valamilyen módon meghatározó befolyása van a szavazás kimenetére.
$\concept{(DEC)}\equiv\concept{DECISIVE}(\rel{V})\defi \exists \mathbb{V} \forall a \exists m \exists n(((m,n)\in \mathbb{X} \land \mathbb{V}\subset\mathbb{N}\land \mathbb{V}\ne\emptyset)\to ((m,n)\in \bigcap\limits_{i \in \mathbb{V}} \rel{P}(\rel{R}_i^a) \to $
$\{m\}=C^a(\{m,n\})))$
(lokálisan) döntő (hun) – (locally) decisive (eng)
$\concept{(ADE)}\equiv\concept{ALMOST\_DECISIVE}(\rel{V})\defi \exists \mathbb{V} \forall a \exists m \exists n(((m,n)\in \mathbb{X} \land \mathbb{V}\subset\mathbb{N}\land \mathbb{V}\ne\emptyset)\to (((m,n)\in \bigcap\limits_{i \in \mathbb{V}} \rel{P}(\rel{R}_i^a) \land $
$(n,m)\in \bigcap\limits_{i \in \mathbb{N} \setminus \mathbb{V}} \rel{P}(\rel{R}_i^a)) \to \{m\}=C^a(\{m,n\}))$
(lokálisan) majdnem döntő (hun) – (locally) almost decisive (eng)
$\concept{(BLO)}\equiv\concept{BLOCKING}(\rel{V})\defi \exists \mathbb{V} \forall a \exists m \exists n(((m,n)\in \mathbb{X} \land \mathbb{V}\subset\mathbb{N}\land \mathbb{V}\ne\emptyset)\to ((m,n)\in \bigcap\limits_{i \in \mathbb{V}} \rel{P}(\rel{R}_i^a) \to $
$m \in C^a(\{m,n\})))$
(lokálisan) blokkoló (hun) – (locally) blocking (eng)
$\concept{(ABL)}\equiv\concept{ALMOST\_BLOCKING}(\rel{V})\defi \exists \mathbb{V} \forall a \exists m \exists n(((m,n)\in \mathbb{X} \land \mathbb{V}\subset\mathbb{N}\land \mathbb{V}\ne\emptyset)\to (((m,n)\in \bigcap\limits_{i \in \mathbb{V}} \rel{P}(\rel{R}_i^a) \land $
$(n,m)\in \bigcap\limits_{i \in \mathbb{N} \setminus \mathbb{V}} \rel{P}(\rel{R}_i^a)) \to m \in C^a(\{m,n\}))$
(lokálisan) majdnem blokkoló (hun) – (locally) almost blocking (eng)
Az itt megadott, a szavazók koalíciójára vonatkozó 'döntő' (decisive) értelmezés eltér a korábban definiált 'ügydöntő' (decisive) tulajdonságtól (☜) amit majd később, a May-tételhez kapcsolódva használunk fel (☜) A majdnem döntő minőség formulája itt azt fejezi ki, hogy a majdnem döntő koalíció tagjai egyhangú véleménye határozza meg a közösségi döntés végeredményét úgy, hogy eközben mindenki más preferenciája pont a koalíció tagjainak preferenciájával ellentétes. Ha tehát a majdnem döntő csoport tagjai mind m-t preferálják n-nel szemben, és rajtuk kívül mindenki más az n-t az m ellenében, legyenek utóbbiak akármennyien, akkor is a koalíció véleménye számít, tehát az m alternatíva lesz a győztes. A majdnem döntő koalíció definíciójában szerepel a koalíción kívüliek ellenkező véleménye, míg a döntő csoport meghatározásából ez a mozzanat hiányzik. Éppen ezért a döntő csoport fogalma általánosabb, mert a definíciójában nincs semmilyen további feltétel kikötve. Kicsit félrevezetőnek is tűnhet a 'majdnem döntő' kifejezés, mert ha a meghatározása szerint a majdnem döntő csoport tagjai a csoporton kívüli összes szavazó egyhangú ellenvéleménye ellenére képesek meghatározni a közösségi végeredményt, akkor felmerülhet a kérdés, hogy a teljes ellenkezés dacára elért győzelemnél mi lehet még erősebb (hogy ne legyen szükség a 'majdnem' jelző alkalmazására). A válasz pedig az, hogy logikailag általánosabb, tehát erősebb az a fogalom (a 'döntő koalíció' fogalma), amire semmilyen feltétel sem vonatkozik. A (majdnem) döntő, illetve a (majdnem) blokkoló koalíció fogalmak még lokálisak abban az értelemben, hogy két adott alternatíva (m és n) összehasonlításán alapulnak, de a definíciók nem követelték meg, hogy minden alterntatívára igazak legyenek a megadott feltételek. Globálissá tehetjük a fogalmakat akkor, ha minden alternatíva összehasonlítására kiterjesztjük a feltételek érvényességét (vagyis az alternatívákra vonatkozóan egzisztenciális kvantorok helyett univerzális kvantorokat alkalmazunk).
$\concept{(GDEC)}\equiv\concept{GLOBALLY\_DECISIVE}(\rel{F})\defi \exists \mathbb{V}\forall a \forall m \forall n(((m,n)\in \mathbb{X} \land \mathbb{V}\subset\mathbb{N}\land \mathbb{V}\ne\emptyset)\to ((m,n)\in \bigcap\limits_{i \in \mathbb{V}} \rel{P}(\rel{R}_i^a) $
$\to \{m\}=C^a(\{m,n\})))$
(globálisan) döntő (hun) – (globally) decisive (eng)
$\concept{(GADE)}\equiv\concept{GLOBALLY\_ALMOST\_DECISIVE}(\rel{F})\defi \exists \mathbb{V} \forall a \forall m \forall n(((m,n)\in \mathbb{X} \land \mathbb{V}\subset\mathbb{N}\land \mathbb{V}\ne\emptyset)\to $
$(((m,n)\in \bigcap\limits_{i \in \mathbb{V}} \rel{P}(\rel{R}_i^a) \land (n,m)\in \bigcap\limits_{i \in \mathbb{N} \setminus \mathbb{V}} \rel{P}(\rel{R}_i^a)) \to \{m\}=C^a(\{m,n\}))$
(globálisan) majdnem döntő (hun) – (globally) almost decisive (eng)
$\concept{(GBLO)}\equiv\concept{GLOBALLY\_BLOCKING}(\rel{F})\defi \exists \mathbb{V} \forall a \forall m \forall n(((m,n)\in \mathbb{X} \land \mathbb{V}\subset\mathbb{N}\land \mathbb{V}\ne\emptyset)\to $
$((m,n)\in \bigcap\limits_{i \in \mathbb{V}} \rel{P}(\rel{R}_i^a) \to m \in C^a(\{m,n\})))$
(globálisan) blokkoló (hun) – (globally) blocking (eng)
$\concept{(GABL)}\equiv\concept{GLOBALLY\_ALMOST\_BLOCKING}(\rel{F})\defi \exists \mathbb{V} \forall a \forall m \forall n(((m,n)\in \mathbb{X} \land \mathbb{V}\subset\mathbb{N}\land \mathbb{V}\ne\emptyset)\to $
$(((m,n)\in \bigcap\limits_{i \in \mathbb{V}} \rel{P}(\rel{R}_i^a) \land (n,m)\in \bigcap\limits_{i \in \mathbb{N} \setminus \mathbb{V}} \rel{P}(\rel{R}_i^a)) \to m \in C^a(\{m,n\}))$
(globálisan) majdnem blokkoló (hun) – (globally) almost blocking (eng)
A döntő-, illetve blokkolóképesség fogalmaira támaszkodva definiálhatjuk az oligarcha (oligarchikus szavazó) és a diktátor (diktatorikus szavazó) fogalmát, amelyekre a lehetetlenségi tételek kifejtése során fogunk hivatkozni. Mind az oligarcha, mind a diktátor fogalma szavazók halmazára vonatkozik, tehát az oligarcha és a diktátor fogalma alatt alapértelmezés szerint koalíciót értünk, ami természetesen megengedi azt, hogy adott esetben a koalíció egyelemű legyen, vagyis az oligarcha vagy a diktátor fogalma valóban egy szavazóra utalhasson (ahogy a terminusok hétköznapi használata ezt megkívánná).$\concept{(OLI)}\equiv\concept{OLIGARCHIC}(\rel{F})\defi \concept{GLOBALLY\_DECISIVE}(\rel{F}) \land \concept{GLOBALLY\_BLOCKING}(\rel{F})$
oligarchikus (hun) – oligarchic (eng)
$\concept{(NOLI)}\equiv\concept{NON-OLIGARCHIC}(\rel{F})\defi \lnot\concept{OLIGARCHIC}(\rel{F})$
oligarchamentes (hun) – nem-oligarchikus (hun) – non-oligarchic (eng)
$\concept{(DIC)}\equiv\concept{DICTATORIAL}(\rel{F})\defi \forall a \forall m \forall n \exists! i\in \mathbb{N}(\rel{F}(\rel{R}^a(m,n))\leftrightarrow \rel{R}_i^a(m,n))$
diktatórikus (hun) – dictatorial (eng)
$\concept{(NODIC)}\equiv\concept{NON-DICTATORIAL}(\rel{F})\defi\lnot\concept{DICTATORIAL}(\rel{F})$
diktátormentes (hun) – nem-diktatórikus (hun) – non-dictatorial (eng)
Az $\rel{F}$ véleményösszegző függvény diktatórikus, ha az általa aggregált kollektív vélemény minden esetben megegyezik egyetlen (az $i.$) szavazó $\rel{R}_i^a(m,n)$ véleményével. [♦] Ha ilyen nincs, akkor a szavazási rendszer nem diktatórikus. Meg kell jegyezni, hogy a diktátormentesség követelménye – a dolgokat a tényleges társadalmi praxis felől szemlélve – nem igazán erős. Az egyszemélyi akarat (a diktatúra) érvényesülését ugyanis ki lehet zárni már azzal is, ha két személy (egy kisebb csoport) véleménye érvényesül. A diktátormentesség megkövetelése a véleménymonopólium kizárását biztosítja, de a véleményoligopóliumét már nem. Bár Arrow már a tétele első megfogalmazásakor definálta és használta a kikényszerítettség fogalmát, a témakör diskurzusában kevesebb figyelmet kapott ez a kategória, ezért én sem szentelek neki több figyelmet. A nem-kikényszerítettség tulajdonságát Arrow az állampolgári szuverenitás (citizen's sovereignty) feltételének is nevezte [K.J.A] A társadalmi jóléti függvényre vonatkoztatható feltételek bemutatása után következhet Arrow lehetetlenségi tételének kimondása: nem létezik olyan társadalmi jóléti függvény, amely minden preferenciaprofilra helyes rendezést eredményez (tehát reflexív, tranzitív és anti-szimmetrikus relációt) és teljesíti az (uni), (Pe), (iia) és (nod) feltételeket.$\lnot\exists \rel{F}(\concept{(UNI)}(\rel{F}) \land \concept{(PE)}(\rel{F}) \land \concept{(IIA)}(\rel{F}) \land \concept{(NODIC)}(\rel{F}))$
Arrow lehetetlenségi tétele (hun) – Arrow's impossibility theorem (eng) – General Impossibility Theorem (eng) – Arrow's paradox (eng)
Arrow saját bizonyítása a diktátor szavazó fogalmára épül. [♦] A tételt az idők során sokféleképpen is bizonyították. Sen két lépésben adta meg a bizonyítást [Amart] Először egy segédtételben kimondta, hogy ha egy aggregálási metódusra teljesül a (uni), a (Pe) és a (iia) feltétel, illetve van legalább egy olyan szavazó, aki az összes alternatívapárra vonatkozóan majdnem döntő, akkor annak a szavazónak diktátornak kell lennie. Második lépésben pedig megmutatta, hogy ha az első három feltétel teljesül, akkor mindig van ilyen majdnem döntő szavazó, aki – a segédtétel értelmében – diktátor is egyben. Másfajta bizonyítást mutatott be Salvador Barber\'{a} [Salva] Bizonyítását egy új fogalomra támaszkodva adta meg, amikor bevezette a pivotális szavazó fogalmát. E fogalommal azt a szavazót jelölte meg, akinek a szavazata fordulópontot jelent a szavazás során, vagyis ha ő megváltoztatja a saját szavazatát, akkor a közösségi döntés maga is megváltozik. A jól ismert, széles körben alkalmazott kollektív döntési eljárások közül, amelyek megsértik valamelyik feltételt a fenti négyből, a többségi eljárás kielégíti a (Pe), a (iia) és a (nod) feltételeket, de az univerzalitási kritériumot már nem [Amart] Sen bemutatott egy konkrét példát arra, hogy a Borda-pontozási rendszer hogyan sérti meg az irreleváns alternatívák függetlensége elvét.| \multicolumn{4}{c}{1. szavazás}&\multicolumn{4}{c}{2. szavazás}\\ | ||||||||||||||
| \multicolumn{2}{c}{preferenciák}&\multicolumn{2}{c}{Borda-pontok}&\multicolumn{2}{c}{preferenciák}&\multicolumn{2}{c}{Borda-pontok}\\ | ||||||||||||||
| 1. szavazó: | $m n o$ | $m:$ | $7= 1\times 3+ 2\times 2$ | 1. szavazó: | $m o n$ | $m:$ | $7= 1\times 3+ 2\times 2$ | |||||||
| 2. szavazó: | $o m n$ | $n:$ | $4= 1\times 2 + 2\times 1$ | 2. szavazó: | $o m n$ | $n:$ | $3= 3\times 1$ | |||||||
| 3. szavazó: | $o m n$ | $o:$ | $7= 2\times 3 + 1\times 1$ | 3. szavazó: | $o m n$ | $o:$ | $8= 2\times 3 + 1\times 2$ | |||||||
Gibbard oligarcha tétele
Érdekes története van Allan Gibbard oligarcha tételének, mert a tételt megfogalmazó írását a szerző sosem publikálta hivatalos helyen, így csak kéziratban terjedt a szakmán belül [Allan] Mégis sokan olvasták, sokan is hivatkoztak rá, úgyhogy az 1969-es születése után nem sokkal a szakmai diskurzus megkerülhetetlen hivatkozási alapjává vált a "cikk". [♦] Gibbard később sem publikálta soha a tanulmányát, de az állandó érdeklődés miatt a 2000-es években saját honlapján elérhetővé tette mindenki számára. A tétel a következő formulával írható le.$|\mathbb{X}|\ge 3 \land (\concept{WEAK\_ORDER}(\rel{R}^m) \lor \concept{LINEAR\_ORDER}(\rel{R}^m)) \land \concept{(PE)}(\rel{F}) \to \concept{(OLI)}(\rel{F})$
Gibbard oligarcha tétele (hun) – Gibbard's oligarchy theorem (eng)
Tegyük fel, hogy az alternatívák halmaza több, mint két elemből áll ($|\mathbb{X}| \ge 3$). Legyen az $\rel{F}$ egy kvázi Arrow-típusú összjóléti függvény, amelyre teljesül a következő két feltétel: (i) az alternatívák értelmezési tartományán képzett rendezett m-esek gyengén rendezettek (☜) vagy lineárisan rendezettek (☜) illetve (ii) érvényesül a Pareto-hatékonyság. Ekkor az $\rel{F}$ függvény oligarchikus.Sen libertárius paradoxona
Az Amartya Sen által először megfogalmazott libertárius paradoxon nemcsak a társadalmi választások elmélete iránt érdeklődők számára vált fontossá, de sok más irányból is felkapták ezt a témát [Amart] [Amart] [Amart] Ennek elsősorban az lehetett az oka, hogy az elemzett problémának, a libertárius viszonyulásban, értékelésben benne rejlő ellentmondásnak nyilvánvalóan erős politikai, értékelvű konzekvenciái voltak. [♦] Sen példája 'Lady Chatterly szeretője' című könyvvel kapcsolatos. Tegyük fel, hogy van két szereplő, M, a prűd, merev gondolkodású és N, a nyitott, érdeklődő ember. [♦] M nem szeretné, ha az általa szabadosnak vélt könyvet bárki elolvasná, mert károsnak tartja a tartalmát (legyen ez az o alternatíva). Ha mégis döntenie kell, hogy kettejük közül ki olvassa el, akkor inkább magát választaná úgy gondolván, hogy ő "ellent tudna állni" a káros hatásoknak (legyen ez az m alternatíva, és legyen n az az opció, amikor N olvasná el a könyvet). Az M számára tehát a következő preferenciarendezés adott: $o m n$. [♦] Ezzel szemben feltételezhetjük azt, hogy a nyitottabb gondolkozású N nemcsak azt szeretné legkevésbé, hogy senki se férhessen hozzá a könyvhöz, de a prüdéria csökkentése érdekében azt pártolná leginkább, hogy M olvassa azt el elsőként. A N rendezése így: $mno$. Ha úgy akarunk közösségi döntést hozni, hogy minimális liberalizmus elvét betartjuk, vagyis tiszteletben tartjuk az egyének döntési jogát ebben a kérdésben, akkor a következőféleképpen érvelhetünk. Mivel M nem szeretné, viszont N szeretné elolvasni a könyvet, ezért az lenne a liberális kollektív döntés, ami igazodna az $om$, valamint az $no$ preferenciákhoz, amiből viszont következik a $nom$ hármas rendezés.| $M$ | $o m n$ | |||||||||||||
| $N$ | $m n o $ | |||||||||||||
| liberális elv | $n o m$ | |||||||||||||
Lehetségességi tételek
Az Arrow tétel és az azt követő további lehetetlenségi tételek azt mutatták meg, hogy mi lehetetlen, vagyis mit nem tehetünk meg, de nyitva hagyták a kérdést, hogy mi lehetséges, vagyis mit tehetünk meg. Tudunk-e pozitív állításokat tenni a társadalmi választási függvényekre vonatkozóan. A válasz természetesen az, hogy igen. Ritkábban szokták idézni, de ettől még tény, hogy Arrow a lehetetlenségi tételéről szóló könyvében foglalkozott azzal a kérdéssel is, hogy vannak-e lehetségességi tételek, és rá is mutatott két esetre, amikor létezhet megoldás. A továbbiakban ezekkel a lehetőségekkel foglalkozom röviden.Black tétel
Duncan Black 1948-ban, tehát még Arrow lehetetlenségi tételének "felbukkanása" előtt megfogalmazott egy tézist, ami egy speciális preferencia esetén az Arrow-féle kritériumok együttes kielégíthetőségét állította [Dunca] Black tézise nem az Arrow-tétel cáfolata, hiszen a preferenciák egy szűkebb tartományára, mégpedig az (spp) egycsúcsú preferenciákra (☜) vonatkozóan áll csak fent az igazsága. Az egycsúcsú preferenciák létét csak úgy feltételezhetjük, ha a választási függvény értelmezési tartományára nem áll fent az univerzalitás kritériuma, vagyis korlátozott tartományról beszélünk. A Black tétel éppen ezért "létezhet" az Arrow-féle lehetetlenségi tétel mellett, mert az előbbi érvénytelenként kezeli az utóbbi egyik alapfeltételét. A Black tétel az alábbi kondicionálissal írható le.$(\rel{F}=\rel{F}^{AP} \land \concept{(SPP)}(\rel{P})) \to (\concept{(NODIC)}(\rel{F}) \land \concept{(IIA)}(\rel{F}))$
Black tétel (hun) – Black theorem (eng)
A Black-tétel értelmében tehát amennyiben az egyéni preferenciák egycsúcsúak, akkor a(z egyszerű) többségi döntési szabály nem diktatórikus és kielégíti az irreleváns alternatívák függetlenségének elvét. Újra csak hangsúlyozom: a Black-tétel úgy tudta megkerülni Arrow lehetetlenségi tételét, hogy korlátozott tartományra vonatkozva mondta ki a lehetségességi tételét.Inada tétel
Ken-ichi Inada különböző preferenciatípusokra mondta ki a konzisztens társas preferencia létezését egyszerű többségi szabály mellett [Ken-i] [Ken-i] Korábban bemutattam, hogy vannak preferenciák, amelyek jól meghatározott profillal rendelkeznek (☜) Ezek közül néhány esetben – Inada alapján – kimondhatunk lehetségességi tételeket a társadalmi választási függvényre vonatkozóan. Idézzük fel Inada preferenciaprofil-típusait.- (dip) – dichotóm preferencia
- (ecp) – visszhangszerű preferencia
- (anp) – antagonisztikus preferencia
- értékkorlátos preferencia
- (spp) – egycsúcsú preferencia
- (sdp) – egyvölgyű preferencia
- (gsp) – szeparált preferencia
- (tap) – tabu preferencia
$(\rel{F}=\rel{F}^{SM}\land ((\concept{(DIP)}\veebar\concept{(ECP)}\veebar\concept{(ANP)}) \veebar ((\concept{(SPP)}\veebar\concept{(SDP)}\veebar\concept{(GSP)}\veebar\concept{(TAP)})\land |\mathbb{N}|=\concept{(ODD)})))\to \concept{TRANSITIVE}(\rel{F})$
Inada tétel (hun) – Inada theorem (eng)
Az Inada tétel középpontjában az az elképzelés áll, hogy a többségi eljárás tranzitivitása nem azonos a racionális döntéssel, valamint, hogy konzisztens társas preferencia létezéséhez a tranzitivitás túl erős követelmény, elég hozzá gyengébb feltétel is [Amart]May tétel
Az Arrow-féle lehetetlenségi tételre azonnal reagált Kenneth O. May, aki egy 1952-es cikkében fejtette ki azt a tételét, amit később róla neveztek el [may:e] May kétalternatívás helyzetet (m és n választási alternatívával), benne minden egyén számára három döntési lehetőséget ($\rel{P}(m,n)$, $\rel{I}(m,n)$, $\rel{P}(n,m)$) feltételezett, és a közösségi döntések jellemzésére bevezette a csoportdöntési függvény (group decision function) kifejezést, ami ugyanaz a fogalmat jelöli, mint a véleményösszegző függvény terminusa. Ezek után megfogalmazott négy feltételt, amelyek teljesülését az $\rel{F}$ csoportdöntési függvénytől "el lehet várni". May elsőként a döntésképesség (decisive) tulajdonságát vezette be. Mivel nem adott pontos formulákat a fogalmaira, ezért a szóbeli leírásait nekünk kell interpretálni és formalizálni. A szakirodalomban ezt a may-i kritériumot leggyakrabban az univerzalitás fogalmával azonosítják [Amart] [Csaji] Ezt a fogalmat korábban már bemutattam (☜) Én kicsit másként értelmezem May felfogását. Szerintem ő azt akarta rögzíteni, hogy a csoportdöntési függvény legyen minden lehetséges bemenetre értelmezve, és minden bemenő értékre adjon egyértelmű kimenetet. Nem véletlen, hogy May maga döntésképesnek (decisive) nevezte ezt a feltételt: a tétel bizonyítása során az egyértelmű végeredmény elvárására hivatkozott. Igaz, hogy ettől még a feltételek közé kell sorolnunk a tetszőleges bemenet "kezelésének" elvárását, tehát az univerzalitást is. Ebből az következik, hogy – megítélésem szerint – May a döntésképes fogalma alatt az $\rel{F}$ választási függvény döntésképes és univerzális jellegét értette. [♦] (☜) May következő két tulajdonsága valamifajta szimmetriát fejez ki – egyfelől a szavazók, másfelől az alternatívák között. A szavazók közti szimmetriát az anonimitás, az alternatívák köztit a semlegesség tulajdonságaival ragadhatjuk meg. A szimmetricitást itt úgy kell érteni, hogy mind a szavazók, mind a választható alternatívák egyenrangúak egymással, nincs egyik sem kivételezett helyzetben a többihez képest, és ebben az értelemben nincs semmiféle aszimmetria közöttük. Az anonimitás definiálásához szükség van egy $\sigma$ segédfüggvényre, amely a szavazók sorrendjét képes tetszőleges módon előállítani (matematikailag ez annyit jelent, hogy a $\sigma: \mathbb{N} \mapsto \mathbb{N}$ függvény a szavazók $\mathbb{N}$ halmazának tetszőleges permutációját képes létrehozni). A segédfüggvény segítségével már meghatározhatjuk az anonimitás tulajdonságát.$\concept{(ANYM)}\equiv\concept{ANONYM}(\rel{F})\defi \forall a \forall b \forall m\forall n\forall i(\rel{F} (\langle \rel{R}^a_i(m,n) \rangle_{i \in \mathbb{N}} ) = \rel{F} (\langle \rel{R}^b_{i}(m,n)\rangle_{i \in \mathbb{N}}))$
anomin (hun) – egalitáriánus (hun) – egalitarian (eng) – anonym (eng)
Az anonimitás feltétele azt jelenti, hogy a csoportdöntés nem változik, ha a bemenő egyéni szavazatok sorrendjét tetszőleges módon megváltoztatjuk. [♦] Ebből azonnal következik, hogy egyfelől mindenki szavazata egyenlőnek számít, másfelől ezáltal teljesíteni lehet az anonimitás követelményét, hiszen a végeredményt tekintve nem számít, hogy ki, mikor, melyik szavazólapon adta le szavazatát. May meg is jegyezte, hogy lehetne ezt a tulajdonságot egalitáriánusnak is nevezni, amely kategória egyértelműen utal a szavazók körében elvárt "egyenlőség" szimmetriájára. A másik szimmetricitási tulajdonság az alternatívákra, jelöltekre vonatkozik. Ahogy a neutralitásnál azt kellett biztosítani, hogy egyik szavazó se legyen se jobb, se rosszabb helyzetben a többihez képest, úgy itt valami hasonlót kell az alternatívákra megkövetelni. Elvárjuk, hogy minden jelölt helyzete legyen ugyanolyan, vagyis az alternatívák egyenlő eséllyel rendelkezzenek, ne legyen köztük bármiféle aszimmetria. Az anonimitás kritériumával azt fejezhetjük ki, hogy a csoportdöntés érzéketlen az alternatívákra, nem kedvez egyik számára sem.
$\concept{(NEUT)}\equiv\concept{NEUTRAL}(\rel{F})\defi \forall a \forall b\forall m\forall n\forall o\forall p((\forall i\forall\sigma(\rel{R}^a_i)(m,n)\leftrightarrow \rel{R}^b_{i})(o,p)) \land (\forall i(\rel{R}^a_i)(n,m) \leftrightarrow \rel{R}^b_{i})(p,o))) $
$\to ((\rel{F} (\langle \rel{R}^a_i(m,n) \rangle_{i \in \mathbb{N}})) \leftrightarrow \rel{F} (\langle \rel{R}^b_{i}(o,p) \rangle_{i \in \mathbb{N}}))\land ((\rel{F} (\langle \rel{R}^a_i(n,m) \rangle_{i \in \mathbb{N}})) \leftrightarrow \rel{F} (\langle \rel{R}^b_{i}(p,o) \rangle_{i \in \mathbb{N}})))$
semleges (hun) – neutral (eng)
A formula értelmezéséhez figyelembe kell venni azt a tényt, hogy May olyan helyzetet feltételezett, amelyben három döntés, tehát háromféle szavazat képzelhető csak el, amit leegyszerűsíthetünk arra, hogy adott alternatívára vagy $igen$-nel vagy $nem$-mel szavaz(hat)tak a szavazók. Ekkor viszont az egy jelöltre leadott igenlő szavazatok komplementer viszonyban vannak a jelöltre nem adott szavazatokkal, és ha ilyenkor minden szavazat esetében megcseréljük a szavazatok minőségét ($igen$-ről $nem$-re és fordítva), majd így végezzük el az összegzést, akkor ugyanazt a végeredményt kell kapjuk. Ha ez a feltétel teljesül, akkor valóban biztosíthatjuk az alternatívák semlegességét, hiszen ebben az esetben nem tudunk különbséget tenni a jelöltek között. Az alternatívák iránti semlegességet csak a döntetlen esetén kell feladni, amikor egy másodlagos, döntetlentörő szabály segítségével kell eldönteni, ki legyen a győztes. Ez a szabály azonban kivételszabálynak minősül, nem tartozik a csoportdöntési függvény magjába. May negyedik kritériumként bevezette a pozitív érzékenység tulajdonságát, amiről ő maga megjegyezte, hogy erősebb Arrow második feltételéhez képest, és amiről mi megjegyezhetjük, hogy ez az új kategória nagyon hasonlít a korábban már bemutatott monotonitás fogalmára (☜)
$\concept{(POSR)}\equiv\concept{POSITIV\_RESPONSIVENESS}(\rel{F})\defi \forall a \forall b \forall m\forall n(\forall i(((\rel{P}_i^a(m,n)\to \rel{P}_{i}^b(m,n)) \land (\rel{I}_{i}^a(m,n) \to $
$\rel{R}_{i}^b(m,n))) \land \exists j((\rel{I}_j^a)(m,n) \land \rel{P}_{j}^b(m,n)) \veebar (\rel{P}_j^a(n,m) \land \rel{R}_{j}^b(m,n)))\to (\rel{R}^a(m,n) \to \rel{P}^b(m,n)))$
pozitív érzékenység (hun) – pozitív reakciókészség (hun) – positive responsiveness (eng)
May azt az interpretációt adta a fogalomra, hogy ha a csoportdöntés m alternatívára nézve kedvező (vagy legalább indifferens), és az egyéni szavazók közül valaki megváltoztatja a korábbi döntését n-ról m-re, akkor a csoportdöntési függvény továbbra is kedvező kell maradjon m-re nézve. Az aggregáló függvények fenti tulajdonságaira, valamint az egyszerű/többségi többségi szavazás (simple majority voting) [♦] eljárásra támaszkodva May a következő tételt fogalmazta meg:$(|\mathbb{X}|=2 \to \rel{F}=\rel{F}^{SM}) \leftrightarrow \concept{DEC}(\rel{F})\land\concept{ANYM}(\rel{F})\land\concept{NEUT}(\rel{F})\land\concept{POSR}(\rel{F})$
May tétel (hun) – May theorem (eng)
A két-alternatívás $\rel{F}$ csoportdöntési függvény akkor és csak akkor (abszolút) többségi szavazás, ha $\rel{F}$ ügydöntő, anonim, semleges és monoton. [♦] A May-tételben az ekvivalenciának mindkét iránya fontos. Egyfelől igaz, hogy ha egyszerű többségi szavazási eljárást alkalmazunk, akkor teljesítjük a fenti négy igazságossági feltételt, másfelől igaz az is, hogy ha a jelzett négy – a méltányosságérzetünket kielégítő – tulajdonság teljesül egy véleményaggregáló függvényre, akkor az egyszerű többségi eljárás lesz. A tétel jelentőségének és helyének érzékeltetéséhez hozzátartozik, hogy tudjuk: csak kétalternatívás közösségi döntési helyzetekben érvényes. A többségi szavazással hozható kapcsolatba a logrolling, a szavazatcsere jelensége, ami a többségi és kisebbségi véleményeket valló emberek csoportjai közti különös viszonyból fakad, a jelenséget azonban csak azután tudom bemutatni (☜) miután már bevezettem a stratégiai szavazás fogalmát.Young tétel
A többségi szavazás mellett gyakran alkalmazott aggregálási technika a pontozásos szavazás, a Borda-pontok módszere, úgyhogy adta magát a kérdés, hogy vajon milyen feltételek mellett alkalmazható ez a szavazási technika. J. Smith cikke volt az első 1973-ban, ami ezzel a kérdéssel foglalkozott [JohnH] de (el)ismertebbé H.P. Young tétele vált, amit Young egy 1975-ös cikkében publikált [H.P.Y] Young a pontozásos módszer alkalmazhatósági feltételeire vonatkozóan újabb tulajdonságokat definiált, és ezekre támaszkodva mondta ki tételét. Két új tulajdonságot vezetett be, és további kettőt használt a korábban definiált tulajdonságok közül. A pontozásos módszer axiomatizálását Young egy korábbi cikkében már elvégezte [young] de ott még - részben – más tulajdonságokat használt. Mivel ekkor már közismert volt, hogy a pontozásos módszer ellentmond az irreleváns alternatívák függetlensége elvének, ezért Young javasolta elhagyni ezt a feltételt. Rögtön javasolt viszont bevezetni két új fogalmat, az egyik egy konzisztenciafeltételt, a másik egy folytonossági elvet fogalmazott meg.
$\concept{(RIF)}\equiv\concept{REINFORCED}(\rel{F})\defi \exists m((\mathbb{N}_1\cup\mathbb{N}_1=\mathbb{N} \land \mathbb{N}_2 \cap \mathbb{N}_2=\emptyset \land C_1(\mathbb{N}_1) \cap C_2(\mathbb{N}_2) \ne \emptyset \land $
$m \in C_1(\mathbb{N}_1)\cap C_2(\mathbb{N}_2)) \to C(\mathbb{N})=C_1(\mathbb{N}_1)\cap C_2(\mathbb{N}_2))$
megerősített (hun) – reinforced (eng) – konzisztens (hun) – consistent (eng)
Ez a konzisztenciakritérium fontos, intuitívnak mondható elvárást fogalmaz meg, amit Young a Pareto-hatékonyság kiterjesztéseként értelmezett. Ha a szavazók két körzetben ($\mathbb{N}_1$ és $\mathbb{N}_2$ csoportban), egymástól teljesen elkülönítve szavaznak ugyanazokra a jelöltekre, az $\mathbb{N}_1$ csoportban a $C_1$, az $\mathbb{N}_2$-ben $C_2$ a győztesek halmaza, és van legalább egy olyan jelölt, aki a győztesek mindkét csoportjában benne van, akkor a két szavazói csoport ($\mathbb{N}_1 \cup \mathbb{N}_2$) szavazatainak összesítése után a győztesek halmaza a két részgyőztes halmazának metszete lesz ($C_1\cap C_2$). Peyton Young a konzisztens terminust használta erre a tulajdonságra, Roger B. Myerson szerint H. Moulin volt az, aki kicserélte ezt a 'reinforcement' terminussal megtartva a fogalom eredeti jelentését [Roger] és a javaslatot Myerson is elfogadta, én pedig a 'reinforcement' terminusát más szófaji alakkal helyettesítettem. A később bemutatandó paradoxonok közül a többkörzetes paradoxonnal (☜) kapcsolatban játszik szerepet ez a kritérium, mert a reinforcement tulajdonság létezése biztosíthatja azt, hogy az adott szavazási módszer esetén ne lépjen fel a többkörzetes paradoxon. A következő tulajdonság értelmezéséhez újra azt kell feltételeznünk, hogy két teljesen elkülönült csoportban zajlik a szavazás ($N_1$ és $N_2$). A két csoportban legyen A és B jelölt a nyertes külön-külön. Ilyen helyzetben fel lehet tenni a kérdést, hogy van-e olyan feltétel, amely mentén ki lehet hozni győztesnek az egyik jelöltet a másik ellenében, ha a két körzetet (csoportot) egyesítjük. Erre az egyik igenlő válasz az lehet, hogy elvárjuk az arkhimédeszi tulajdonság érvényesülését, amit egyszer már megragadtunk a sorrendezés vagy archimédeszi rendezés fogalmával (☜)$\concept{(CONT)}\equiv\concept{CONTINUOUS}(\rel{F})\defi \concept{ARCHIMEDEAN\_ORDER}(\rel{F})$
folytonos (hun) – continuous (eng) – arkhimédeszi (hun) – Archimedean (eng) – ellenállhatatlan többség (hun) – overwhelming majority (eng)
Az újonnan definiált arkhimédeszi tulajdonság akkor áll fenn, ha az egyik csoport részgyőztesét úgy hozhatjuk ki az egyesítés utáni győztesnek, hogy egy kellően nagy számmal beszorozzuk a csoport létszámát, és ezáltal a győztesre leadott szavazatok számát, amivel már le lehet győzni a másik csoport részgyőztesét. Ugyanezt a minőséget fejezi ki az arkhimédeszi preferencia fogalma is, amit máshol elemezek a könyvben (☜) Az 'ellenállhatatlan többség' kifejezést Roger B. Myerson javasolta, [♦] mint ami tartalmilag legpontosabb fejezi ki a szóban forgó tulajdonságot [Roger] Az újonnan bevezetett tulajdonságokat kettő korábban definiált kritériummal kiegészítve Young már megfogalmazhatta saját lehetségességi tételét, amelyben a Borda-pontozási függvényre vonatkozóan tett állítást.$\concept{(SCR)}(\rel{F}) \leftrightarrow \concept{(ANYM)}(\rel{F})\land \concept{(NEUT)}(\rel{F}) \land \concept{(RIF)}(\rel{F}) \land \concept{(CONT)}(\rel{F})$
Young tétel (hun) – Young theorem (eng)
A tétel azt mondja ki, hogy egy társadalmi döntési módszer akkor és csak akkor lehet anoním, semleges, megerősített és folytonos, ha az a pontozásos szabály. Young összetett tulajdonságokat is képzett, és részben ezekre támaszkodva mondta ki tételét (így például az anoním és semleges függvényt Young szimmetrikusnak nevezte, amivel pusztán csak azt akarta kifejezni, hogy az adott eljárás mind a szavazókat, mind az alternatívákat egyenlő módon, elfogultság nélkül kezeli).No-show paradox
A monotonitás feltétele magától értetődőnek tűnik, hiszen ha egy alternatívára több szavazat érkezik, akkor azt érezzük intuitívnek, hogy ez a többletszavazat ne rontson az alternatíva helyzetén. Mégsem mindig ez a helyzet. Vannak olyan összegzőeljárások, amelyek megsértik a monotonitási tulajdonságot. Fishburn és Brams cikkéből idézhetünk ide egy példát szemléltetésképpen [Fishb] Egy kisvárosban három jelölt indul a polgámesteri címért: Mrs. Bitt, Mr. Huff és dr. Wogg. A szavazás során a Hare-féle preferenciális szavazás eljárását alkalmazzák. Ennek a lényege röviden annyi, hogy ha az első preferenciaként megadott jelöltek közül valaki megszerzi a szavazatok felét, akkor ő nyer. Ha nem ez a helyzet, akkor az első helyes szavazatok alapján kihúzzák a legkevesebb szavazatot szerző jelöltet, és a többi alternatívára szűkítve folytatják tovább az eljárást – az első fordulóhoz hasonló logika mentén. [♦] A szavazás során mindenkinek meg kell adnia a szavazólapon, hogy milyen sorrendben támogatja a három jelöltet. A szavazás napján a Smith házaspár kocsija lerobban útban a szavazóhelység fele, és lekésik a szavazást. Mindkettejük preferenciája megegyezett az alábbi minta szerint: Bitt > Huff > Wogg, tehát a szavazólapra a BHW sorrendet írtak volna. A másnapi újságban megjelent a hír, miszerint a választást Mr. Huff nyerte. Közölték a szavazási eredményeket is.| szavazatok | sorrendek | H > W | W > H | |||||||||||
| 417 | BHW | 417 | 0 | |||||||||||
| 82 | BWH | 0 | 82 | |||||||||||
| 143 | HBW | 143 | 0 | |||||||||||
| 357 | HWB | 357 | 0 | |||||||||||
| 285 | WBH | 0 | 285 | |||||||||||
| 324 | WHB | 0 | 324 | |||||||||||
| 1608 | 917 | 691 | ||||||||||||
| Bitt | 499 (417 + 82) | |||||||||||||
| Huff | 500 (143 + 357) | |||||||||||||
| Wogg | 609 (285 + 324) | |||||||||||||
| szavazatok | sorrendek | B > W | W > B | |||||||||||
| 419 | BHW | 419 | 0 | |||||||||||
| 82 | BWH | 82 | 0 | |||||||||||
| 143 | HBW | 143 | 0 | |||||||||||
| 357 | HWB | 0 | 357 | |||||||||||
| 285 | WBH | 0 | 285 | |||||||||||
| 324 | WHB | 0 | 324 | |||||||||||
| 1610 | 644 | 966 | ||||||||||||
| szavazatok | sorrendek | H > W | W > H | |||||||||||
| 419 | BHW | 419 | 0 | |||||||||||
| 80 | BWH | 0 | 80 | |||||||||||
| 143 | HBW | 143 | 0 | |||||||||||
| 357 | HWB | 357 | 0 | |||||||||||
| 287 | WBH | 0 | 287 | |||||||||||
| 324 | WHB | 0 | 324 | |||||||||||
| 1610 | 919 | 691 | ||||||||||||
Reprezentációs paradoxon
Az előző fejezetben tárgyalt problémához sok szepontból hasonlít a reprezentáció paradoxona, amit Thomas Schwartz írt le először 1985-ben [Schwa] Schwartz azt a közkeletű nézetet támadta meg, amely szerint a közösségi döntési helyzetekben valamilyen vélemény képviseletének sikeressége mindig arányos a véleményt képviselő reprezentációs erő nagyságával. Másként, kicsit konkrétabban mondva: ha egy szavazótestületben (például parlamentben) egy véleménycsoport (például egy párt) érvényesíteni szeretné a véleményét, akkor annál biztosabban teheti ezt meg, minél több szavazattal rendelkezik. Schwartz szerint nem mindig van ez így. Előfordulhat, hogy a kevesebb szavazat, pontosabban az alacsonyabb reprezentációs szint előnyösebb kimenetet eredményezhet.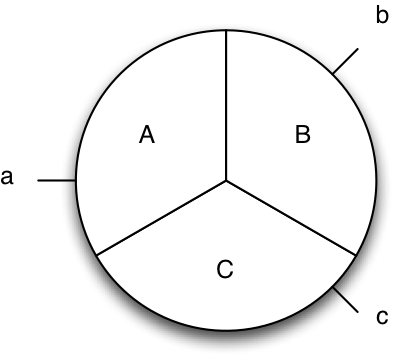
Ebben a történetben három körzethez (A-hoz, B-hez, C-hez) tartozó 100 képviselőnek kell dönteni abban a kérdésben, hogy építsenek-e új haditengerészeti bázist vagy ne, és ha igen, akkor hova. A döntés pillanatában már van egy bázis, az a pontban, és a lehetséges döntések között van az az eset is, hogy minden marad a régiben, nem épül új hadikikötő (status quo). Három hely közül csak az egyiken lehet támaszpont, mert túl drága lenne kettőt fenntartani, viszont egyet mindenképpen meg kell finaniszírozni. A három körzet és a három potenciális bázis helyét, ezek egymáshoz való viszonyát mutatja az ábra. A szavazócsoportokat (pártokat, lobbicsoportokat stb.) a körzetek nevével tudjuk azonosítani. Az A csoportba 23, a B-be 28, a C-be 49 mandátum (szavazási lehetőség) tartozik. A három körzet képviselői rendre a következő preferenciákkal rendelkeznek.
| körzet | szavazatszám | preferencia | ||||||||||||
| $A$ | 23 | $a b c$ | ||||||||||||
| $B$ | 28 | $b c a$ | ||||||||||||
| $C$ | 49 | $c a b$ | ||||||||||||
| körzet | szavazatszám | preferencia | ||||||||||||
| $A$ | 25 | $a b c$ | ||||||||||||
| $B$ | 24 | $b c a$ | ||||||||||||
| $C$ | 51 | $c a b$ | ||||||||||||
Szavazatmanipuláció
A társadalmi választások kimenetét elsődlegesen az egyéni szavazók által leadott szavazatok határozzák meg. Már az is egy kérdés, hogy miért úgy szavaznak, ahogy szavaznak, és tudjuk jól, hogy a végeredményt azáltal is lehet módosítani, megváltoztatni, hogy az egyéni szavazók véleményére próbálnak meg hatást gyakorolni még a szavazás előtt, esetleg a szavazás során. Az előzetes véleménybefolyásolás, a lojalitáskialakítás és lojalitásfenntartás, a kampányolás indirekt technikái többnyire legális módokon hatnak, míg a szavazás közben alkalmazott direkt befolyásolási technikák (például nyílt szavazás során kifejtett nyomásgyakorlás) döntően illegálisak, de ettől még létez(het)nek. Bármennyire is fontosak ezek a befolyásolási jelenségek, velük itt – egyetlen kivételtől eltekintve – nem foglalkozom. Ezen a ponton azt mondom, vegyük tudomásul, hogy a szavazók valamilyen módon, korábban kialakult véleménnyel, preferenciarendezéssel érkeznek el a szavazás pillanatához. Ideális esetben ennek megfelelően adják le a szavazatukat, amikoris azt mondhatjuk, hogy őszintén szavaztak, vagyis mindenféle stratégiai megfontolás nélkül pontosan a saját preferenciáiknak megfelelően adják le a szavazataikat. Elképzelhető azonban az is, hogy mégsem ez a helyzet, vagyis vannak szavazók, akik valamiért az elsődleges/eredeti preferenciáktól eltérnek a szavazás során. Érdemes megfontolni, hogyan is nevezzük az ilyen helyzeteket, mert bár sokféle kifejezés verseng e tárgyban, ezek némelyike rossz konnotációt hozna be a diskurzusba. A stratégiai szavazás vagy taktikai szavazás még értéksemleges, a hazug szavazó (liar) vagy manipulatív szavazó (manipulation of voter) kifejezéseknek már egyértelműen negatív felhangja van. Akármelyik terminust is használjuk, a lényeg persze nem változik. Azt is látni kell azonban, hogy az a definíciós mozzanat, miszerint minden szavazás stratégiai, amennyiben nem a tényleges preferenciarendezése alapján szavaz valaki, nagyon hétköznapi, nagyon gyakori jelenségekre is ráhúzható. Eszerint ugyanis már azt is stratégiai szavazásnak kell tartanunk, ha egy politikai választáson két nagy párt és egy kis párt jelöltjei közül egy szavazó inkább valamelyik nagy párt politikusára szavaz, noha szíve szerint a kis párt politikáját követné. Ha viszont tudja, hogy a két nagy versengése mellett a kicsinek esélye sincs megnyerni a választást, és így a kis pártra adott szavazata "elveszne", nem értékesülne, és ezért inkább a neki szimpatikusabb nagy párt képviselőjére teszi le a voksát, akkor már stratégiai, hazug, manipulatív szavazónak kell minősítenünk. Lehet azon vitatkozni, ki mennyire érzi hazugnak, manipulatívnak az ilyen magatartást, de itt nem az ilyen helyzetek gyakorlati értékelését, hanem csak ezek elméleti leírását szeretném elvégezni. [♦] A stratégiai szavazás során tehát a szavazó azért ad le az igazi preferenciájához képest eltérő, tehát "színlelt" szavazatot, mert azt előnyösebbnek véli az eljárás végeredményét tekintve. Nézzük meg egy egyszerű példát erre a jelenségre [P.Fal] Legyen három alternatíva (U, B, L) és a szavazólapokon lehesen mindegyik alternatívára szavazni úgy, hogy a teljes rendezés során az első alternatíva kapjon 2 pontot, a második 1 pontot, a harmadik ne kapjon semmit (ez a Borda-szavazásnak felel meg). A táblázat baloldali része mutatja az egyenes, tiszta szavazás eredményét, amikor mindenki a valósi preferenciáinak megfelelően szavazott. A jobb oldalon látható a stratégiai (színlelt) szavazás eredménye, ami olyan módon állt elő, hogy mindhárom szavazótábor úgy szavazott, hogy megcserélte a második és harmadik helyen álló alternatíváit.| &\multicolumn{3}{c}{egyenes szavazás}&\multicolumn{3}{c}{színlelt szavazás}\\ | ||||||||||||||
| LBU | BLU | UBL | LUB | BUL | ULB | |||||||||
| szavazat | 104 | 98 | 7 | 104 | 98 | 7 | ||||||||
| pontszám | 306 | 307 | 14 | 208 | 203 | 216 | ||||||||
Szavazatcsere
A szavazatcsere (logrolling) vagy szavazatkereskedelem (voting trade) jelenségét ugyan a stratégiai szavazás körébe kell sorolnunk, mégis érdemes önálló fejezetben tárgyalni. A jelenségnek vannak ugyanis olyan jellemzői, amelyek túlmutatnak a szavazás, azon belül is a stratégiai szavazás intézményén. Minél inkább a szavazatcsere interakciós vonásaira koncentrálunk, vagyis minél inkább figyelembe vesszük a jelenségben rejlő dinamikát, annál inkább távolodunk el az egyszerű szavazás jelenségétől, és közeledünk másfajta, dinamikus módon kezelhető társadalmi kapcsolatokhoz. Na, de nézzük meg, mit is jelent a logrolling jelensége. A megértéséhez abból a megállapításból kell kiindulnunk, hogy a (többségi) szavazás nem veszi figyelembe az egyéni preferenciák intenzitásában meglevő különbségeket [Bucha] Egy adott ügy iránt nagyon elkötelezett ember egyetlen támogató szavazata ugyanannyit ér, mint egy majdnem teljesen közömbös szavazóé, aki valamiért ellenző szavazatot ad le. Amikor ilyen érzelmi intenzitáskülönbségek tapasztalhatók a szavazók körében, akkor lehet értelme a szavazatcsere intézményének. Ha ugyanis az erősen elkötelezett támogató hajlandó valamilyen előnyt kínálni az addig a másik oldalon álló fél támogató szavazatának megszerzéséért, és az az egy szavazat megváltoztatása épp elég ahhoz, hogy a szavazás végeredménye megforduljon, akkor mindkét résztvevő jobban járhat a logrolling révén. Az elkötelezett ember nyereménye a szavazási eredmény megváltozása, a közömbös szavazó pedig a szavazatáért kapott előny miatt jobban járhat, mint anélkül. A logrolling alkalmazása így Pareto-optimális helyzetet teremthet. Nézzünk meg egy példát [David] Legyen két kérdés ($\phi$ és $\psi$), amiben három szavazónak (A-nak, B-nek és C-nek) kell döntenie, és a két kérdés elfogadásához rendeljük a következő nyereményeket (illetve veszteségeket). Ezekből a két kérdés elfogadása esetén származó nettó társadalmi nyereséget is ki lehet számolni.| $\phi$ esetén | $\psi$ esetén | $\phi$-re | $\psi$-re | |||||||||||
| $A$ nyereménye | -100 | -100 | $A$ szavazata | nem | nem | |||||||||
| $B$ nyereménye | -200 | 500 | $B$ szavazata | nem | igen | |||||||||
| $C$ nyereménye | 600 | -300 | $C$ szavazata | igen | nem | |||||||||
| nettó társadalmi nyereség | 300 | 100 | többségi szavazat | nem | nem | |||||||||
| &\multicolumn{3}{c}{szavazatcsere nélkül}&\multicolumn{3}{c}{szavazatcserével}\\ | ||||||||||||||
| A-i út | B-i út | C-i út | A-i út | B-i út | C-i út | |||||||||
| $A$ városrész lakóinak szavazata | igen | nem | nem | igen | igen | nem | ||||||||
| $B$ városrész lakóinak szavazata | nem | igen | nem | igen | igen | nem | ||||||||
| $C$ városrész lakóinak szavazata | nem | nem | igen | nem | nem | igen | ||||||||
| többségi szavazat | nem | nem | nem | igen | igen | nem | ||||||||
Csalásbiztos eljárás
Miután "kiderült", hogy egyfelől a tényleges társadalmi gyakorlatban létezik a stratégiai szavazás intézménye, másfelől az erre reflektáló elméletekben is meg lehet ragadni, jellemezni lehet a jelenséget, akkor felmerül a kérdés, vajon vannak-e olyan társadalomtechnikák, amelyek segítségével meg lehet akadályozni vagy legalább meg lehet nehezíteni azt, hogy emberek "csaljanak", hazudjanak a preferenciáinkat illetően. Van-e – szavazatmanipulációs szempontból vett – csalásbiztos aggregálási technika? A válasz az, hogy bizonyos helyzetekben elképzelhető. Nézzünk meg egy példát Csontos László egyik cikkéből [Csont] amelyben a következő történet szerepelt a Clarke-adó mint csalásbiztos technika hasznával kapcsolatban. Képzeljünk el egy szigeten elterülő kisvárost, ahol felmerül egy híd építésének az ötlete a sziget és a szárazföld között. Ilyenkor hihetőnek tűnik azt is feltételezni, hogy a városka lakói között lesznek, akik ellenzik, és lesznek, akik támogatják az ötletet. Ha nem akarják, hogy egy ilyen fontos kérdésben a többségi akarat alapján döntsenek, mivel az a vesztes kisebbségre túl nagy "terheket" róna, ezért más döntési technikát kell keresni. A következő megfontolásból lehet kiindulni. Minél erősebben támogatja vagy ellenzi valaki a tervet, annál inkább hajlandó lehet pénzzel is támogatni a híd felépítését, ha támogatja a tervet, vagy – épp ellenkezőleg – hajlandó lehet kárpótlást fizetni azért az ötlet támogatóinak, hogy ne épüljön meg a híd. Ezt a – pro és kontra – fizetési hajlandóságot kellene valahogyan figyelembe venni a döntés során. A probléma csak az, hogy egy egyszerű szavazás során nem könnyű biztosítani azt, hogy a szavazók megvallják a többiek számra ezeket az elköteleződéseiket. Az ellenzők igyekeznének úgy szavazni, hogy ne derüljön ki, hogy ők hajlandóak lennének kárpótlásra, míg a támogaták azt nem fednék fel szívesen, mennyire érné meg nekik az ötlet megvalósítása. Az egyik megoldása lehet ennek a problémának az ún. Clarke-adó kivetése. Ennek logikáját akkor érthetjük meg jól, ha egy táblázatban feltüntetjük, hogy az érintetteknek (háztartásoknak) milyen fizetési hajlandóságaik vannak (amikor is feltételezhetjük, hogy ezek a felajánlások nyilvánosak és egyben igazak).| &\multicolumn{2}{c}{fizetési hajlandóság (\$-ban)}&\multirow{2}{*}{Clark-adó}\\ | ||||||||||||||
| háztartás | híd mellett | híd ellen | ||||||||||||
| 1. háztartás | 0 | 9000 | 0 | |||||||||||
| 2. háztartás | 0 | 6000 | 0 | |||||||||||
| 3. háztartás | 0 | 1000 | 0 | |||||||||||
| 4. háztartás | 4000 | 0 | 0 | |||||||||||
| 5. háztartás | 17000 | 0 | 12000 | |||||||||||
| összes háztartás | 21000 | 16000 | 0 | |||||||||||
Gibbard-Satterthwaite tétel
A szavazás során lehetséges manipuláció további lehetőségét jelenti a taktikai szavazás (tactical voting) intézménye. Ebben az esetben a szavazó tudja befolyásolni a végeredményt azzal, hogy nem a valós preferenciái szerint, azaz nem őszintén szavaz abban a reményben, hogy ezzel a maga számára kedvezőbb végeredmény születik a szavazás során. Sok más manipulációs lehetőséghez képest ez bizonyos értelemben talán a "legdemokratikusabb" formája a manipulációnak, hiszen míg a manipulációs lehetősége a legtöbb esetben csak kevesek számára adottak, a taktikai szavazással elvileg mindenki élhet. A taktikai szavazást a szavazatok manipulációjának is mondhatjuk. A szavazatmanipulációval kapcsolatos leghíresebb tételt ketten is kimondták nagyjából egyidőben, Allan Gibbard [Gibba] illetve Mark Allen Satterthwaite [Satte] ezért kettejük nevét összekötve hivatkoznak a "közös" Gibbard-Satterthwaite tételre. Gibbard azzal indítja az elemzését, hogy a preferenciaaggregálási függvények (vagy ahogy Gibbard nevezi őket: a szavazási sémák) a – játékelméleti értelemben vett – játékok speciális eseteit jelentik. Ahogyan megadunk egy játékot, ugyanúgy kell leírni egy szavazási sémát is. Ami a játékokban a stratégiát jelenti, az a szavazásban megfelel egy adott preferenciarendezésnek (egy leadott szavazatnak). Ez a hasonlóság azonban még kevés ahhoz, hogy megragadhassuk a stratégiai szavazás jelenségét. Az igazi, illetve a hazug szavazatok "kezeléséhez" még tudnunk kell azt is, hogy az adott játékos (szavazó) melyik preferenciarendezése az "igazi", az őszinte és melyik nem (tehát stratégiai). Ezt megadhatjuk egy függvénnyel, ami minden szavazóhoz hozzárendeli a lehetséges preferenciarendezések halmazából az egyetlen őszinte preferenciarendezést. A manipulálhatóság tulajdonsága ezek alapján viszont már nem a játékok, hanem csak a szavazások sajátosságaként értelmezhető. Meg kell tehát adni, hogy mit jelent az, hogy egy szavazási eljárás manipulálható vagyis az szavazók számára lehetővé teszi a taktikai szavazást. Ehhez be kell vezetnünk egy segédfogalmat, a feltételes preferenciaprofil fogalmát, amivel azt a helyzetet lehet kifejezni, amikor egy és csak szavazó meg változtatja saját preferenciarendezését, miközben mindenki más kitart a szavazata mellett.$\langle\rel{R}^c_i\rangle_{i\in\mathbb{N}}\equiv \langle\rel{R}^a_i\rangle_{i\in\mathbb{N}}/\rel{R}^b_i \defi \forall j \exists a \exists b((i\ne j \to \rel{R}^c_i = \rel{R}^a_i) \land (i=j)\to \rel{R}^c_i = \rel{R}^b_i)$
feltételes preferenciaprofil (hun) – conditional preference profil (eng)
$\concept{(MAN)}\equiv\concept{MANIPULABLE}(\rel{F})\defi \exists a \exists b \exists i(\rel{P}_i(\rel{F}(\langle\rel{R}^a_i\rangle_{i\in\mathbb{N}}/\rel{R}^b_i ),\rel{F}(\langle\rel{R}^a_i\rangle_{i\in\mathbb{N}}))) $
manipulálható (hun) – manipulable (eng) – színlelt szavazás (hun) – stratégiai (szavazás) (hun) – taktikai (szavazás) (hun) – strategic (voting) (eng) – tactical (voting) (eng) – sophisticated (voting) (eng) – insincere (voting) (eng)
$\concept{(STRP)}\equiv\concept{STRATEGY-PROOF}(\rel{F})\defi \lnot \concept{MANIPULABLE}(\rel{F})$
színlelésbiztos (hun) – nem manipulálható (hun) – hazugságbiztos (hun) – őszinte (voting) (hun) – strategy-proof (eng) – non-manipulable (eng) – sincere (voting) (eng) – straightforward (voting) (eng)
[♦] Csak az egyértelműség kedvéért rögzítem, hogy ezek a tulajdonságok két dologra is vonatkozhatnak. Egyfelől irányulhatnak magára a szavazásra, azaz a szavazat leadásának aktusára, másfelől vonatkozhatnak a szavazási eljárás egészére. Az egyéni szavazó lehet a taktikai szavazó, a szavazási rendszer lehet színlelésbiztos, nem manipulálható vagy épp fordítva, lehet manipulálható, de nem mondhatjuk, hogy az eljárás taktikai vagy stratégiai lenne (legfeljebb csak azt, hogy az eljárás megengedi vagy épp megakadályozza a taktikai vagy stratégiai szavazást). A színlelésbiztosság tulajdonságára támaszkodva már fel lehet írni Gibbard és Satterthwaite tételét.$(\concept{(STRP)} \land \concept{(UNI)})\to \concept{(DIC)}$
Gibbard-Satterthwaite tétel (hun) – Gibbard-Satterthwaite theorem (eng)
A tétel szerint egy legalább háromszemélyes helyzetben nincs olyan racionális döntési mechanizmus, amely egyszerre kielégítené az univerzalitás (uni) és a színlelésbiztosság (strp) feltételét, és eközben nem-diktatórikus (nodic) maradna. [♦] A tételből következik: ha azt akarjuk elérni, hogy a racionális döntés őszinte, taktikai szavazásoktól mentes legyen, azaz mindenki a legpreferáltabb alternatíváját nyilvánítsa ki, akkor szükségképpen a racionális választás elitista/diktatórikus jellegű lesz, azaz lesz egy olyan diktátor, aki a döntési helyzetben belül 'túl nagy' hatalommal rendelkezik, és preferenciája automatikusan kollektív preferenciává válik. A Gibbard-Satterthwaite tétel széleskörű elfogadásával párhuzamosan megindult a tétel finomítása, újraértelmezése, újfajta bizonyításokat dolgoztak ki. Salvador Barber\'{a} alternatív bizonyítást adott a tételre a pivotális szavazó fogalmára támaszkodva [Barbe] Alan D. Taylor pedig megmutatta [Taylo] hogy az Arrow-tétel és a Gibbard-Satterthwaite tétel ekvivalens egymással.McKelvey tétel
A lehetetlenségi tételek egymást kizáró feltételeket állapítanak meg a közösségi vélemény-aggregálások világában. A preferenciákkal kapcsolatos lehetetlenségi tételek sorában az Arrow-tétel mondta ki a legfontosabbat: amikor az egyéni véleményeket összegezzük, nem úszhatjuk meg a diktatórikus mozzanatot, a közösségi vélemények kialakításakor valaki(k) mindig döntő szerepbe kerül(nek). A Gibbard-Satterthwaite tétel azzal pontosította mindezt, hogy ráirányította a figyelmet a stratégiai szavazás, a szavazatmanipuláció jelenségére. A tétel középpontjában két egymást kizáró feltétel került, amelyek közül választanunk kell: a szavazási rendszerünk vagy az őszinte szavazást vagy a diktátormentességet biztosíthatja, a kettőt együtt nem. A most bemutatandó, harmadik lehetetlenségi tétel szerint a szavazás során minden megtörténhet (anything might happen), mert a szavazás lebonyolítása, a szavazási napirend vagy menetrend (agenda setting) kialakítása olyan erőt ad annak kezébe, aki e fölött rendelkezik, amivel bármilyen végeredményt ki tud hozni. És ez a végeredmény nyilvánvalóan az az alternatíva lesz, amit ő (a napirendkezelő) legjobban preferál. Richard Drummond McKelvey volt az, aki 1976-ban írt egy cikket, amiben megfogalmazta a – később róla elnevezett – tételét [McKel] amit aztán némely ponton kiegészített, módosított egy három évvel későbbi tanulmányában [McKel] Érdekes kapcsolatot jelez az a tény, hogy nagyon gyakran káosz-tételként hivatkoznak McKelvey tézisére. A káosz metafora használatának azonban vannak előzményei. Harold Hotelling első tétele óta (☜) a preferenciák kezelésére, értelmezésére a téri metaforát használták. Duncan Black tétele (☜) az egycsúcsú preferenciák (☜) létezése esetén áll fent, és ez a feltétel természetesen nem mindig teljesül. Nem is teljesülhet minden esetben, hiszen az Arrow-tétel pont ennek lehetőségét tagadja. A Black-tételt így lehetségességi tételként is értelmezhetjük, és feltehetjük a kérdést, vajon vannak-e másfajta feltételek, amelyek alapján ki lehetne másfajta lehetségességi tételeket is mondani. Természetesen léteznek további ilyen feltételek és tételek. 1966-ban Plott cikkében megírta, hogy a preferenciák sugaras vagy radiális szimmetriája (radial symmetry) esetén a többségi eljárás diktátormentesen is képes racionális végeredményt produkálni. 1972-ben Otto A. Davis, Morris H. DeGroot és Melvin J. Hinich bebizonyította az euklideszi preferenciákra, hogy $W(x^\ast) = \emptyset$ nyerőhalmaz eleme(i) akkor és csak akkor többségi Condorcet-győztes(ek), ha megegyeznek a teljes mediánnal (total-median) [Davis] A lehetségességi tételek feltételei összefüggenek egymással: a Black-tételben kihasznált feltétel, a preferencia egycsúcsúsága speciális esete a sugaras szimmetriának, utóbbi pedig a teljes medián egyik altípusa [GaryW] Ezek a feltételek azonban nem mindig teljesülnek a tényleges társadalmi gyakorlatban. McKelvey meg is jegyezte egy helyen, hogy a teljes medián követelménye olyan erős, hogy gyakorlatilag lehetetlen kielégíteni. Minél több szavazó van, annál könnyebb megsérteni az elvet, hiszen elegendő egyetlen szavazó preferenciájának miniális megváltoz(tat)ása, és borul a feltételekben megfogalmazott kényes egyensúly [McKel] McKelvey az 1976-os cikkében még feltételezte a preferenciákra vonatkozóan az euklideszi tulajdonság létezését, vagyis azt, hogy az alternatívák tere euklideszi, de az 1979-es tanulmányában ezt tovább általánosította, amikor az euklideszi tér feltételezése helyett elegendőnek tartotta tetszőleges topológiai tér létezését. David Austen-Smith és Jeffrey Banks 1999-ben pedig azt bizonyította be, hogy az euklédeszi preferencia feltételezése helyett elég lehet a folytonossági feltétel rögzíteni [Auste] McKelvey gondolatmenetének kiindulópontjában egy olyan lehetségességi tétel áll, amely kimondja ugyan, hogy a többségi szabály biztosíthatja a Condorcet-győztest bizonyos feltételek mellett, ám McKelvey ezek után épp azt mutatja meg, hogy ez az elvi lehetőség – az alternatívák terében tapasztalható kaotikus viszonyok miatt – gyakorlatilag sosem valósulhat meg. Emiatt húzható rá a káosz-tétel minősítés. A tétel formulája a következő.$(|\mathbb{X}|>2 \land |\mathbb{N}|>2\land \concept{(CONT)}(\rel{F})) \to \concept{(DICT)}(\rel{F})$
McKelvey (káosz) tétel (hun) – McKelvey (chaos) theorem (eng)
A tétel szerint tehét ha több, mint három szavazó van, és legalább három politikai kérdés van napirenden, akkor a döntési folyamat nem diktátormentes. Ebből viszont már levezethető az is, hogy ilyen esetben a napirendet a "diktátor", azaz a napirendkezelő (agenda setter) fogja irányítani (feltételve, ha ismeri a többiek preferenciáit, illetve az ügyletnek nincsenek – komoly – tranzakciós költségek).AI-válasz
A társadalmi választások elméletének egyik kulcseleme az aggregálási, választási eljárás fogalma. A közösségi döntések meghozatalához szükséges választási eljárások matematikai algoritmusok, így nem kell azon meglepődnünk, hogy az 1990-es évektől kezdve megjelentek matematikusok, mérnökök, informatikusok is ezen a kutatási terepen. A formális eszközök iránti igény korábban is vonzotta az ilyen felkészültségű szakembereket ide. Miután egyre másra jelentek meg olyan új feladatok, amikor számítástechnikai környezetben kellett szimulálni ilyen-olyan választási helyzeteket, [♦] érthető, hogy a fejlesztések, fejlesztők oldalán is erősödött az igény a szavazáselméletek tanulságainak becsatlakoztatására. Az azonban mégiscsak meglepő, hogy milyen technikákat hoztak be ebbe az új diskurzusba az informatika, matematika oldaláról. Ahhoz, hogy érteni lehessen, milyen fogalmakkal, elméletekkel operálnak a mérnökök, informatikusok ezen a terepen, tudnunk kell valamit a témánk szempontjából nagyon fontos bonyolultságelmélet világából. A számítástechnika fejlődése során a matematikusok, informatikusok sokat foglalkoztak az algoritmusok problémakörével. Az egyik kiemelten fontos kérdés az volt számukra, hogy milyen számítási feladatot jelentenek a különféle algoritmusok a gépek számára, vagyis mennyi idő szükséges valamely probléma megoldására, a hozzá tartozó algoritmus lefuttatására. Anélkül, hogy a fogalmak lényegi tartalmát, és főleg a mögöttük levő elméleteket megértenénk, szükségünk van arra, hogy tudjuk, milyen fogalmak mit jelentenek, mire és miért használják őket a mérnökök. P- és NP-problémáról, illetve utóbbiakon belül NP-nehéz és NP-teljes problémáról szoktak beszélni. Nekünk csak annyit kell tudni, hogy ezek a megoldandó feladatok bonyolultságát, és a megoldáshoz szükséges számításigény nagyságrendjét fejezik ki. A P osztály a polinom időben megoldható problémákból áll, azaz olyan problémákból, melyekhez létezik olyan k konstans, hogy a probléma n hosszú bemenet esetén $O(n^k)$ idő alatt megoldható. Ez annyit jelent, hogy az ide tartozó algoritmusok vállalható idő alatt lefutnak a számítógépeken. Ezzel szemben az NP-nehéz (NP-teljes) osztályba tartozó problémák olyanok, hogy nagy elemszám mellett gyakorlatilag megoldhatatlanok. A megoldhatatlanságot itt csak abban az értelemben kell érteni, hogy kiszámíthatatlanok, vagyis ha elindítanánk tetszőleges képességű és méretű számítógépen a problémát elvileg megoldani képes algoritmust, akkor az sosem jutna a futási idő végére. Elvileg tehát megoldható lenne, csak gyakorlatilag nem számítható ki. Ezek a problémaosztályok "normál ügymenetben" kihívást jelentenek a matematikusok számára, amikor a cél az ilyen bonyolult problémák megoldása valamilyen eszköz, trükk segítségével. Kiderült azonban, hogy nagyon praktikus haszna is lehet az ilyen problémáknak. Praktikus védelmet jelenthetnek ugyanis olyan helyzetekben, amikor valamilyen informatikai erőforráshoz való hozzájutást effajta problémák megoldásának közbeiktatásával lehet megfelelő módon kezelni ("csak akkor léphetsz be ezen a ponton, ha megoldod ezt a problémát"). A NP-osztályba tartozó feladatok tehát egyfajta kapuőrként is használhatók. Ez a kifordított gondolat segített abban, hogy a mérnökök megjelenjenek a szavazáselméletek világában és használni kezdjék ezeket a bonyolultságelméleti fogalmakat. Ha ugyanis az a feladat, hogy megakadályozzuk az – egyéni vagy koalíciós – stratégiai szavazás lehetőségét, akkor erre meg kell keresni, és ha van, hasznosítani kell azokat a számítástechnikai eszközöket, amelyek más területeken már beváltak. Az 1990-es évek kezdetén Bartholdi szerzőtársaival olyan megoldásokat dolgozott ki, amelyek a fenti elveket ültették át a gyakorlatba. Kiderült, hogy a társadalmi választási eljárásokat valóban annál kevésbé lehet manipulálni, minél bonyolultabbak ezek az eljárások algoritmuselméleti szempontból. Ez praktikusan azt jelenti, hogy az aggregálási mechanizmusok integritásának a szükséges számításigény értelmében vett komplexitás az igazi biztosítéka [J.Bar] [Barth] Bartholdiék megoldási javaslatai mind a jelöltek, mind a szavazók számára nagy számokat írtak elő, így tudták biztosítani a megfelelő számítási bonyolultságot. Vincent Conitzer, Tuomas Sandholm és Jérôme Lang azzal érveltek, hogy a jelöltekre vonatkozó számossági elvárások nem mindig életszerűek, hiszen a választási helyzetek egy részében csak kevés alternatíva közül kell választani, ezért olyan számításokat végeztek, és ezek alapján olyan új javaslatokat tettek le az asztalra, amelyek úgy biztosítottak megfelelő számítási bonyolultságot az egyes választási eljárásokkal kombinálva, hogy a kisebb jelöltszám esetében is működött a dolog [V.Con] Tanulmányukban először röviden bemutatták, milyen dimenziókban, milyen kérdések mentén vizsgálják a jelenséget. Kik a manipulátorok? Lehetnek egyéni vagy csoportos, koalícióba szerveződő szavazók. Mit tudnak a manipulátorok a tiszta szavazók szavazatairól, preferenciáiról? Lehet teljes vagy tökéletlen a tudásuk. Súlyozottak-e vagy sem a szavazók? Ezáltal lehet különbséget tenni különböző szavazótípusok, szavazók között (például részvényesi szavazás során). Mi a manipuláció célja? Vagy az, hogy egy adott jelölt nyerjen (ekkor beszélhetünk konstruktív szavazásról), vagy az, hogy ne nyerjen (ez a destruktív szavazás). A vizsgálatba bevontak 9-10 szavazási módszert, és a fenti szempontok alapján sorra mondtak ki tételeket arra vonatkozóan, hogy a különböző feltételek mentén adott eljárások esetében adott (2-7 fős) jelöltszámok mellett milyen számítási problémát jelent a manipulációs szavazás végrehajtása (megakadályozása). Csak a szemléltetés kedvéért bemutatok itt egy táblázatot a cikkből, ami a súlyozott, koalíciós, konstruktív manipulációkkal kapcsolatos adatokat tartalmazza.| jelöltek száma | 2 | 3 | 4, 5, 6 | $\ge$7 | ||||||||||
| Borda | P | NP-teljes | NP-teljes | NP-teljes | ||||||||||
| véto | P | NP-teljes | NP-teljes | NP-teljes | ||||||||||
| STV | P | NP-teljes | NP-teljes | NP-teljes | ||||||||||
| kétfordulós többségi | P | NP-teljes | NP-teljes | NP-teljes | ||||||||||
| Copeland | P | P | NP-teljes | NP-teljes | ||||||||||
| maximin | P | P | NP-teljes | NP-teljes | ||||||||||
| randomizált kupa | P | P | P | NP-teljes | ||||||||||
| reguláris kupa | P | P | P | P | ||||||||||
| többségi | P | P | P | P | ||||||||||
Párosításelmélet
A kollektív preferenciák kezelésének egy speciális területét jelentik azok a problémák, amelyeket a párosításelmélet vizsgál a hatvanas évek elejétől fogva. David Gale és Lloyd S. Shapley írta le először azt a problémát, amit párosítási feladatnak, majd később a problémát leíró elméletet párosításelméletnek neveztek el [D.Gal] A probléma megoldásra Shapleyék egy olyan algoritmus javasoltak, ami a mai napig Gale-Shapley algoritmus néven ismert és hivatkozott szerte a világban. A stabil házasítási vagy párosítási probléma (stable matching problem) arról szól, hogy össze kell párosítani lányokat és fiúkat egymással azok preferenciarendezései alapján a lehető legoptimálisabb módon, vagyis úgy, hogy mindeki a lehető leginkább kedvelt partnerével kerülhessen egy párba. A stabil megoldást itt úgy értelmezhetjük, hogy a kapcsolatok között nincs egyetlen blokkoló pár sem, vagyis nem létezik olyan fiú-lány kettős, akik nem házastársak, de mindketten boldogabbak lennének egymással a jelenlegi párjukhoz képest. Ezt úgy is fogalmazhatjuk, hogy ha egy fiú és egy lány nem házas, akkor legalább az egyikük jobban szereti a jelenlegi házastársát, ezért nem lehet őt elcsábítani, vagyis az algoritmus válásbiztos (divorce-proof). Azt természetesen nem várhatjuk el, hogy minden esetben mindenkit össze lehessen kapcsolni a legjobban akart partnerével, de azt mindenképpen biztosítani kell, hogy mindenki olyan jelöltet kapjon a végén, aki rajta van a preferencialistáján (vagyis mindenki találjon magának valakit a preferencialistájáról). [♦] Shapleyék erre a feladatra dolgozták ki azt az algoritmust, ami végül is képes volt minden esetben stabil megoldást szállítani. A késleltetett elfogadási algoritmus (deferred acceptance algorithm) lényege az, hogy a fiúk minden körben felkérik a lányokat a preferencialistájuk alapján, [♦] hogy legyenek a párjuk (táncpartnerük stb.), a lányok pedig a kérők közül a nekik legjobban tetsző fiúknak feltételes igen-t (talán-t) mondanak (ha van ilyen), míg a többieknek nem-et. Az elküldött fiúk a következő körben felkérik a preferencialistájukon szereplő következő lányt. A lányok az új kérőket elutasítják, ha azok hátrébb vannak, mint a már esetleg talán-nal talonba tett fiú vagy ha annál jobb helyen áll az új jelölt, akkor lecserélik a régit az újra. A lecserélt fiú újra beáll a kérők közé, és a következő fordulóban – a többi visszautasított társával együtt – megy a preferencialistája következő helyén szereplő lányhoz. Ekkor a lányok újra választanak. Ez így megy addig, amíg minden fiú ki nem köt valahol, vagyis amíg talán választ nem kap. Mivel a jelenség szemléltetésére Gale és Shapley nehezebben követhető példát adott, ezért itt inkább egy Biró Péter és társai által bemutatott példát ismertetek [biro_] A példában szereplő négy lány és négy fiú az alábbi sorrendben szeretne magának társat választani.| lányok rangsorai | fiúk rangsorai | |||||||||||||
| Anna: | Gábor > Henrik | Endre: | Dóra > Anna > Bea > Csilla | |||||||||||
| Bea: | Gábor > Ferenc > Endre > Henrik | Ferenc: | Dóra > Csilla > Anna > Bea | |||||||||||
| Csilla: | Gábor > Henrik > Endre > Ferenc | Gábor: | Dóra > Csilla > Bea > Anna | |||||||||||
| Dóra: | Henrik > Gábor | Henrik: | Bea > Anna > Csilla | |||||||||||
| 1. kör | 2. kör | 3. kör | 4. kör | |||||||||||
| Anna | Endre | $\underline{Henrik}$ | ||||||||||||
| Bea | $\underline{Henrik}$ | $\underline{Henrik}$ | $\underline{Endre}$, Henrik | $\underline{Endre}$ | ||||||||||
| Csilla | $\underline{Ferenc}$ | $\underline{Ferenc}$ | $\underline{Ferenc}$ | |||||||||||
| Dóra | Endre, Ferenc, $\underline{Gábor}$ | $\underline{Gábor}$ | $\underline{Gábor}$ | $\underline{Gábor}$ | ||||||||||
"Vegyük észre, hogy az itt vizsgált központosított piacok nem jelentenek központi tervezést, ahogyan a legtöbben ezt értelmezik, mivel ezek a piacok úgy lettek megalkotva, hogy érzékenyek legyenek a szereplők kinyilvánított preferenciáira, ahelyett, hogy egy tervező ezektől független céljainak elérését szolgálnák. Ami itt központosítva van, az nem az elérendő cél, hanem a piaci mechanizmus maga." idézi: [BiroP]
Mielőtt foglalkoznék még a késleltetett elfogadási algoritmus náhány fontos következményével, bemutatom, hogy lehet a tételt formális módon leírni. Amennyiben $\mathbb{M}$-vel jelöljük a férfiak halmazát, $\mathbb{W}$-vel a nőkét, $>_a$-vel valamely a ágens preferenciarendezését és $\mu$-vel ($\mu:\mathbb{M}\cup\mathbb{W}\mapsto \mathbb{M}\cup\mathbb{W}$) a párosítási függvényt, akkor néhány tulajdonság definiálása után formálisan is megadhatjuk a Gale-Shapley tételt, miszerint a házassági problémának mindig létezik stabil megoldása.$\exists m\exists w(\mu(m)=w\leftrightarrow \mu(w)=m) \land \forall w \forall m((\mu(w)\in\mathbb{M}\lor \mu(w)=w)\land (\mu(m)\in\mathbb{W} \lor \mu(m)=m))$
párosítás(i függvény) (hun) – matching (function) (eng)
$\concept{BLOCKED\_INDIVIDUALLY}(\mu)\defi \exists a\in\mathbb{M}\cup\mathbb{W}(a >_a \mu(a))$
egyénileg blokkolt párosítás (hun) – matching blocked individually (eng) – matching blocked by an individual (eng)
$\concept{BLOCKED\_COLLECTIVELY}(\mu)\defi \exists w\in\mathbb{W} \exists m\in\mathbb{M}(w >_m \mu(m)\land m >_w \mu(w))$
párosan blokkolt párosítás (hun) – matching blocked collectively (eng) – matching blocked by a pair of agents (eng)
$\concept{STABLE}(\mu)\defi \lnot \concept{BLOCKED\_INDIVIDUALLY}(\mu) \land \lnot\concept{BLOCKED\_COLLECTIVELY}(\mu)$
stabil párosítás (hun) – stable matching (eng)
$\exists \mu (\concept{STABLE}(\mu))$
Gale-Shapley tétel (hun) – Gale-Shapley theorem (eng)
A tételre Gale és Shapley konstruktív bizonyítást adtak, amikor megmutatták, hogy az algoritmust, aminek alkalmazásával mindig el lehet jutni a feladat stabil megoldásához [D.Gal] Annak ellenére, hogy a házasítási problémának mindig van stabil megoldása, azért az is fontos tény, hogy ez az algoritmus nem mindig és nem mindenkinek biztosítja a legjobb párosítást. A Gale-Shapley algoritmus ismeretében Lester E. Dubins és David A. Freedman egy 1981-es cikkben feltette a kérdést, hogy abban az esetben, ha a játékosok között vannak olyanok, akik ismerik a többiek preferenciáit, akkor van-e esélyük arra, hogy a saját preferenciakinyilvánításaik megváltoztatásával befolyásolják az algoritmus menetét és ezzel a végerdményt – nyilván úgy, hogy számukra kedvezőbb lehessen. Lehet-e manipulálni, érdemes-e hazudni, vagyis lehet-e itt machiavellizmusról beszélni – tette fel a kérdést Dubins és Freedman [L.Dub] A válasz az volt, hogy az egyetemek esetében elképzelhető, hogy némelyiküknek előnyösebb lehet hazudni, azonban a hallgatók esetében ez a lehetőség már nem áll fent. [♦] Minden hallgatóra (és azok minden koalíciójára) igaz, hogy az algoritmus biztosítja a legjobb stabil megoldást számukra, és ezen nem tudnak semmilyen taktikázással javítani. Dubinsék cikkére válaszul David Gale és Marilda Sotomayor példát és bizonyítást hozott arra, hogy több stabil illeszkedés esetén a másik irányban mindig lehetséges hazugsággal előnyt szerezni legalább egy szereplő számára [D.Gal] [♦] Sok más tétel és alkalmazási lehetőség lenne még bemutatható a késleltetett elfogadási algoritmussal kapcsolatban, de ezek elemzésével itt nem foglalkozom tovább. Az elmélet további tételeiről, az elméleti eredmények konkrét gyakorlati alkalmazásairól értő összefoglalást nyújt Alvin Roth 2008-as áttekintő tanulmánya [A.E.R]Körzethatár-manipuláció
Az egyéni vélemények közösségi véleményekké transzformálásának következő befolyásolási lehetősége a körzetesítés vagyis a körzethatárok megváltoztatása (gerrymandering). Itt azokról a körzethatárokról van szó, amelyek meghatározzák az aggregálási számítások alapjául szolgáló területi egységeket. Még pontosabban: a földrajzi térben szétszórtan elhelyezkedő szavazópolgárokat egy-egy szavazataggregációs közösségbe egybefogó határokról van szó, amelyeket természetesen – mindig és szükségszerűen önkényes – politikai döntések határoznak meg. Ez a körzetesítés így mindig rendelkezik valamilyen mértékű manipulációs potenciállal. Mielőtt bemutatnék egy egyszerű példát a körzethatárok átszabásában rejlő manipulációs lehetőségre, fel kell hívnom a figyelmet arra, hogy két fontos körzetfogalmat el kell különítenünk egymástól, nem szabad őket összekevernünk egymással. A szavazatokat szavazókörökben gyűjtik össze. Ezeket a körzeteket kicsire kell szabni, mert igazodni kell ahhoz az elváráshoz, hogy a szavazópolgárok kis fáradsággal fel tudják keresni. A szavazókörökhöz így viszont csak kevés embert lehet hozzárendelni, amiből következően a mandátumokat sem lehet egy-egy szavazókörben kiosztani. Ezért van szükség a választókerület fogalmára, ami a mandátumok kiosztásának területi egysége. Természetesen szükség van arra is, hogy kapcsolatot teremtsünk a kétféle körzetfogalom között, vagyis összerendeljük a szavazatok összegyűjtésének színtereit, a szavazóköröket és a mandátumok kiosztásának egységeit, a választókerületeket egymással. Akármilyen elveket is rögzítünk azonban, amikhez igazodni kell a szavazókörök és választókerületek párosításakor, mindig marad hely az eseti (önkényes) döntésnek, és ez adja a körzethatár-átszabások elvi lehetőségét. Ezek alapján nézzük meg, hogyan is működhet ez. Képzeljük el, hogy van két párt, harminchat szavazókörzet. Feltételezzük fel még, hogy minden körzetben ugyanannyi ember szavaz, és az egyszerűség kedvéért tegyük fel azt is, hogy minden szavazókörzetben az egyik vagy másik pártra adják le az összes szavazatot (ez ugyan életszerűtlen feltételezés, de a lényeget ez nem érinti). Tegyük fel még fel azt is, hogy egy-egy mandátumot lehet kiosztani négy választókerületben. A kérdés már csak az, hogy a harminchat szavazókörből hogyan csináljunk négy választókerületet, ahol egy-egy mandátumot lehet nyerni. A következő ábrán a harminchat szavazókör kétféle választókerületi besorolását mutatom be.
A szürke és fehér négyzetek jelölik az egyik vagy másik pártra egységesen szavazó szavazóköröket (nevezzük a két pártot fehér és szürke pártnak). A választókerületi felosztást jelzik a szavazókörök köré rajzolt körzethatárok. Ha egyszerű többségi szavazással döntünk, akkor nagyon eltérő végeredményt ad a két felosztás. A baloldali besorolás alapján a négy választókerület mindegyikében a fehér párt nyeri el a mandátumot, míg a jobboldali felosztásban a szürke párt három, a fehér párt egy mandátumot kap. Bár a gerrymandering valóban létező, "művelhető" manipulációs lehetőség és technika, ahhoz képest, hogy mennyire sokat hivatkoznak rá, nincs akkora potenciál benne. Sok országból, sok történelmi helyzetből lehet példákat hozni arra, hogy alkalmazták, sőt, sokszor sikerrel alkalmazták ezt a technikát, de ettől még tudni kell a helyén kezelni a dolgokat. Mivel az 1990-ben megállapított választókerületi határok sok esetben nem feleltek meg a törvényi előírásoknak (az időközben lezajlott népmozgalmi folyamatok eredményeként), 2008-ban készítettünk egy olyan alkalmazást, ami a 2006-os parlamenti választások adataira támaszkodva, bizonyos paramétereket szabadon változtatva átszabta a választókerületek határait. [♦] Bár az alkalmazás használatakor különböző paramétereket beadva egészen eltérő választókerületi határokat és ezzel eltérő szimulált végeredményeket lehetett kihozni, az is kiderült az ilyen próbálkozásokból, hogy nagyon radikálisan eltérő végeredményeket nem lehetett elérni, akárhogy is változtak a körzethatárok. [♦]
Többkörzetes paradoxon
Sorolhatnánk a körzetmanipuláció, a gerrymandering fogalma alá azt a körzethatárokkal kapcsolatos jelenséget, amit Peter C. Fishburn és Steven J. Brams szerzőpáros többkörzetes paradoxonnak nevezett el, és amire egy 1983-as cikkében mutatott be egy szemléltes példát [Fishb] A helyzet azonban pont fordítva van. A többkörzetes paradoxon létezése biztosítja a körzethatár-manipuláció elvi lehetőségét, vagyis az előbbi jelenség logikailag megelőzi az utóbbit. A többkörzetes paradoxon ugyanis azt a helyzetet írja le, amikor a szavazatokat – a szavazók térhez való kötöttsége miatt, tehát pusztán gyakorlati okokból – körzetekbe rendezve gyűjtik össze, és a szavazási adatok összegzése során paradoxon adódik. Ha nem lennének körzetek, akkor nem adódna semmi gond, de ha vannak körzetek, akkor paradoxon keletkezhet. És ha már van paradoxon, akkor az ilyen helyzeteket már lehet manipulálni, vagyis akkor már helye van a gerrymanderingnek is. A többkörzetes paradoxon tehát az alap, de még nem tudjuk, miről is szól pontosan ez a paradoxon. A no-show paradoxon kapcsán korábban már bemutatott kisváros (☜) szavazási anomáliái közé tartozik ez az új eset is. Bramsék cikkének főszereplője, Mrs. Smith csinált egy újabb kimutatást a kisvárosi választás adatai alapján. A szavazást két szavazókerületre bontva, egy keleti és egy nyugati körzeten belül végezték el a városka lakói. Az adatok így a két körzetre bontva is rendelkezésre álltak Mrs. Smith számára. Az alábbi táblázat mutatja a különböző preferenciasorrendekre leadott szavazatokat a két körzet szerinti bontásban.| összes szavazat | sorrendek | keleti körzet | nyugati körzet | |||||||||||
| 417 | BHW | 160 | 257 | |||||||||||
| 82 | BWH | 0 | 82 | |||||||||||
| 143 | HBW | 143 | 0 | |||||||||||
| 357 | HWB | 0 | 357 | |||||||||||
| 285 | WBH | 0 | 285 | |||||||||||
| 324 | WHB | 285 | 39 | |||||||||||
| 1608 | 588 | 1020 | ||||||||||||
| jelöltek | keleti körzet | nyugati körzet | ||||||||||||
| Bitt | $160 (160 + 0)$ | $339 (257 + 82)$ | ||||||||||||
| Huff | $143 (143 + 0)$ | $357 (0 + 357)$ | ||||||||||||
| Wogg | $285 (0 + 285)$ | $324 (285 + 39)$ | ||||||||||||
| jelöltek | keleti körzet | nyugati körzet | ||||||||||||
| Bitt | $303 (160 + 143 )$ | $624 (257 + 82 + 285)$ | ||||||||||||
| Huff | $396 (357 + 39)$ | |||||||||||||
| Wogg | $285 (0 + 285)$ | |||||||||||||
Többesetes paradoxon
Bizonyos értelemben a választási paradoxonok vég nélkül szaporíthatóak, ezért fontos kérdés, hogy ezek között vannak-e olyanok, amelyek visszavezethetők valamely más paradoxonra. A többkérdéses vagy többesetes választás paradoxona (multiple-elections paradox) jelenségét egy 1998-ban megjelent cikkben Steven J. Brams, D. Marc Kilgour és William S. Zwicker nevezte meg először [S.J.B] és bár a cikk végén megmutatták azt is, hogy a jelenség értékelhető a szavazási paradoxon egyik változataként, mégis önálló névvel, újfajta minőséggel hivatkoztak erre a problematikára. A paradoxon olyan választási helyzetekben jelentkezhet, amelyekben egyfelől egyszerre több témában is szavazni kell, másfelől mindegyik témában igen vagy nem lehet a választási lehetőség. Bramsék az egyes témákat, szavazási kérdéseket propozícióknak, míg az összes szavazási kérdés együttesét kombinációnak nevezték el. Az ilyen szavazások során a szavazókat annyiféle szavazói profilba sorolhatjuk be, ahány szavazatkombináció lehetséges elméletileg. Ha valóban csak ${igen/nem}$ értékek közül lehet választani, akkor k szavazási kérdés esetén a szavazatkombinációk száma összesen $k^2$ lehet. Az egyes szavazók által leadott tényleges szavazatkombinációkat mindig besorolhatjuk valamelyik szavazatkombináció-profilba, és összeszámolhatjuk, mennyi szavazat érkezett összesen ezekre. A szavazatkombinációkat az adott sorszámú kérdésre adható igen vagy nem szavazatok szerint I-vel vagy N-nel jelölhetjük, tehát egy szavazatkombináció mindig annyi I vagy N betűből áll, ahány kérdést tesznek fel a választás során. Hogy miként lesz ebből paradoxon, érthetővé válik, ha megnézünk egy konkrét példát. Tegyük fel, hogy három kérdésről kell szavazni, csak $igen/nem$ válasz lehetséges, 13 szavazónk van, és az alábbi szavazatok érkeztek az egyes szavazatkombinációkra.| profilok | $III$ | $IIN$ | $INI$ | $INN$ | $NII$ | $NIN$ | $NNI$ | $NNN$ | ||||||
| szavazatok | 1 | 1 | 1 | 3 | 1 | 3 | 3 | 0 | ||||||
| profilok | $IIII$ | $IIIN$ | $IINI$ | $INII$ | $NIII$ | $IINN$ | $ININ$ | $INNI$ | ||||||
| szavazatok | 0 | 4 | 4 | 4 | 4 | 1 | 1 | 1 | ||||||
| profilok | $NIIN$ | $NINI$ | $NNII$ | $INNN$ | $NINN$ | $NNIN$ | $NNNI$ | $NNNN$ | ||||||
| szavazatok | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 5 | ||||||
| kombináció | DDD | DDR | DRD | DRR | RDD | RDR | RRD | RRR | ||||||
| 1976 | 40,8 | 5,7 | 2,6 | 1,9 | 11,7 | 8,2 | 8,5 | 20,6 | 100% (n=316) | |||||
| 1980 | 22,2 | 2,5 | 2,2 | 0,6 | 16,8 | 12,7 | 14,3 | 28,6 | 100% (n=315) | |||||
Anscombe-paradoxon
A G.E.M. Anscombe nevével jelzett paradoxon a többségi elv egy furcsa deficitjére mutat rá [G.E.M] A jelenség szemléltetésére Anscombe adott egy példát, amelyben tizenegy szavazó (A,B, …, K) tizenegy kérdésről szavazott. Az eredményt mutató táblázatban az $igen$ szavazatokat 1, a $nem$-eket 0 jelöli. Mivel a többségi szavazással hozott csoportdöntés minden esetben $igen$ (1) volt (6:5 arányban), ezért azt mondhatjuk, hogy az egyéni $igen$ (1) szavazatok sikeres voltak, mivel a csoportdöntéssel megegyeztek, az egyéni $nem$-ek pedig sikertelenek.| A | B | C | D | E | F | G | H | I | J | K | csoportdöntés | |||
| 1. kérdés | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | ||
| 2. kérdés | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | ||
| 3. kérdés | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | ||
| 4. kérdés | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | ||
| 5. kérdés | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | ||
| 6. kérdés | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| 7. kérdés | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| 8. kérdés | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | ||
| 9. kérdés | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | ||
| 10. kérdés | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | ||
| 11. kérdés | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | ||
| sikeres szavazat | 4 | 4 | 4 | 4 | 4 | 4 | 5 | 9 | 9 | 9 | 10 | |||
| kérdések: | $A$ | $B$ | $C$ | |||||||||||
| 1. szavazó véleménye | igen :-) | igen | nem | |||||||||||
| 2. szavazó véleménye | nem | nem :-) | nem | |||||||||||
| 3. szavazó véleménye | nem | igen | igen :-) | |||||||||||
| 4. szavazó véleménye | igen :-) | nem :-) | igen :-) | |||||||||||
| 5. szavazó véleménye | igen :-) | nem :-) | igen :-) | |||||||||||
| többségi vélemény | igen | nem | igen | |||||||||||
"Amikor a többséget képviselők megkapják, amit akartak, ezt a kisebbség frusztrációja árán érik el ugyan, de legalább senki sincs kivételezett helyzetben … annak a módszernek, amely úgy ad eredményt, hogy minden személy vágyához [szavazatához] egyenlő súlyt rendel, a lehető legnagyobb számú vágyat [szavazót] kell kielégítenie, hogy a legjobb és legigazságosabb legyen." [G.E.M]
Még durvább a helyzet, ha az előző táblázatban bemutatott szavazói vélemények létezését feltételezve és képviseleti demokráciát "szimulálva" olyan jelöltekre kell szavazni, akik a három kérdésben előre kinyilvánítják a preferenciáikat, és ez alapján szavaznak rájuk a szavazók. Tegyük fel, hogy két jelölt van, az alábbi "ígéretekkel".| kérdések: | $A$ kérdés | $B$ kérdés | $C$ kérdés | |||||||||||
| 1. jelölt meghirdetett profilja | igen | nem | igen | |||||||||||
| 2. jelölt meghirdetett profilja | nem | igen | nem | |||||||||||
| 1. kérdés | 2. kérdés | 3. kérdés | ||||||||||||
| 1. szavazó véleménye | Y :-) | Y | Y :-) | |||||||||||
| 2. szavazó véleménye | X | X :-) | Y :-) | |||||||||||
| 3. szavazó véleménye | X | Y | Y :-) | |||||||||||
| 4. szavazó véleménye | Y :-) | X :-) | X | |||||||||||
| 5. szavazó véleménye | Y :-) | X :-) | X | |||||||||||
| többségi vélemény | Y | X | Y | |||||||||||
Osztrogorszkij paradoxon
Noha Mojszej Jakovlevics Osztrogorszkij [♦] már az 1900-as évek elején írt arról a paradoxonról, amit később róla neveztek el, a társadalmi választások elméletével foglalkozó kutatók csak a hetvenes években figyeltek fel erre a problémára [Hannu] A paradoxon lényege a következő. Legyen három kérdéskör, és négy választói csoport ($A,B,C,D$), amelyek a szavazók 20-20-20-40 százalékát reprezentálják valamint két párt (X és Y). Tegyük fel, hogy a három kérdésben a választói csoportok az alábbi táblázat szerint szavaznak a két párt (programjai) közül valamelyikre.| csoport | 1. kérdés | 2. kérdés | 3. kérdés | támogatott párt | ||||||||||
| $A$ (20%) | $X$ | $X$ | $Y$ | $X$ | ||||||||||
| $B$ (20%) | $X$ | $Y$ | $X$ | $X$ | ||||||||||
| $C$ (20%) | $Y$ | $X$ | $X$ | $X$ | ||||||||||
| $D$ (40%) | $Y$ | $Y$ | $Y$ | $Y$ | ||||||||||
| győztes párt (1) | - | - | - | $X$ | ||||||||||
| győztes párt (2) | $Y$ | $Y$ | $Y$ | $Y$ | ||||||||||
| szavazók | képviselőház | szenátus | kormányzóság | |||||||||||
| 1-3 szavazó | D | D | D | |||||||||||
| 4 szavazó | D | D | R | |||||||||||
| 5 szavazó | D | R | D | |||||||||||
| 6 szavazó | D | R | R | |||||||||||
| 7-9 szavazó | R | D | R | |||||||||||
| 10-12 szavazó | R | R | D | |||||||||||
| 13 szavazó | R | R | R | |||||||||||
Véleményaggregálás
A közösségi döntések alapkérdése évtizedeken kereszül az volt, hogy az egyéni preferenciák aggregálásának milyen jellemzői, esetleg milyen problémái vannak. Sokáig evidencia volt, hogy a közösségi döntéseket az egyéni preferencirendezések alapján kell meghozni. A vélemény egyet jelentett a preferenciarendezések kifejezésével, a véleményaggregáláson pedig a preferenciaaggregálást kellett érteni. Az 1990-es évek azzal hozták el fordulatot e téren, hogy a véleményaggregálás fogalma alá besorolva megjelentek azok a cikkek, amelyek a kijelentések aggregálásának problémáival kezdtek el foglalkozni. Innentől kezdve a véleményaggregálás (judgement aggregation) már két dolgot jelenthetett: a hagyományos értelemben vett preferenciaaggregálást és az újonnan "érkezett" kijelentésaggregálást. [♦] A következőkben utóbbi problémakör fontosabb kérdéseit tekintem át.Doktrinális paradoxon
Miközben Wijnand J. Schoenmakers egy 1986-os kétoldalas cikkében az adatbázisok egyesítésének veszélyeire akarta felhívni a figyelmet, a probléma forrását egy olyan képzeletbeli példával szemléltette, ami teljes mértékben alkalmas arra, hogy a véleményaggregálás problámájára is rá lehessen mutatni vele [Schoe] Schoenmakers történetében egy bíró két tanút kérdezett ki különböző időpontokban. Az első tanú azt állította, hogy az A állítás igaz, a második pedig azt, hogy az $A \to B$ összetett kijelentés igaz. A két kijelentés alapján a bíró levonta azt a következtetést, hogy B is igaz (és erre hivatkozva halálra ítélte a vádlottat). Később kiderült, hogy mindkét tanú hamisnak tartotta a B állítást, bár más indokok alapján. Az első tanú nem gondolta sem B-t, sem $(A \to B)$-t igaznak, de mivel a bíró ezt nem kérdezte tőle, nem szólt semmit erről. A második tanú pedig úgy vélte, hogy az $A \to B$ állítás igaz ugyan, de tudta azt is, hogy a B nem. Ebből levonhatta magának a következtetést, hogy akkor az A nem lehet igaz, de ezt magától értetődőnek tartotta, ezért ezt nem is mondta el a bírónak. A két tanútól átvett állítások alapján a bíró helyes logikai következtetést vont le, ám mégis rossz ítéletet hozott. Példájával Schoenmakers azt akarta szemléltetni, hogy a különböző forrásokból származó adatok egyesítése könnyen ellentmondásokhoz vezethet. A mérnökök, informatikusok számára azért volt fontos mindez, mert az ilyen paradoxon lehetősége komoly fenyegetést jelenthet az adatbázisok egyesítése során, mivel az egyébként önmagukban konzisztens adatbázisok az egyesítés után (az egyesítés eredményeként) inkonzisztenssé válhatnak. A történet tanulsága azonban messze túlmutat az adatbázisok egyesítésének problémáján. Ugyanez a probléma rejlik a doktrinális paradoxon mélyében. A doktrinális paradoxon (doctrinal paradox) vagy más néven bírói paradoxon problémáját Kornhauser és Sager fedezte fel [Kornh] Kornhauserék felismerése az volt, hogy ha egy ügyben nem egyetlen, hanem több bíró dönt valamiért (ahogy Amerikában a fellebbviteli bírósági tárgyalások esetében ez így van), és többségi eljárással összegzik a bírók véleményeit, akkor könnyen paradoxonhoz juthatunk. Nem mindegy ugyanis, hogy a döntéshozatal melyik fázisában összegzik az egyéni véleményeket. Az egyik megoldás szerint előbb közösen tisztázni kell a tényállást. Ehhez a büntethetőséget implikáló egyes feltételekről kell közös véleményt kialakítani, és minden tényállási kérdésben többségi szavazást kell alkalmazni. Az egyes feltételekre így megállapított közös vélemény alapján lehet aztán a büntetésre vonatkozó konklúziót levonni. Létezik azonban egy másik módszer is, ami szerint mindenkinek magának kell döntenie a tényállási feltételeről, és a közösségi döntésre csak – az egyéni döntések alapján – a bűnösség kimondásakor, az ítélethozatal során van szükség. Egy egyszerű példa segítségével szemléltethető, hogy miként juthatunk így ellentétes eredményekhez [Kornh] Tegyük fel, hogy egy olyan ügyben kell dönteni, amelyben két szempont (A és B) alapján kell megállapítani, hogy bűncselekmény történt-e, amit szankcionálni kell (S) vagy sem ($\lnot S$). A két feltétel és a szankció legyen a következő.| $A$ | – $x$ és $y$ között érvényes a szerződés |
| $B$ | – $x$ megszegte a szerződést |
| $S$ | – $x$ kártérítésre kötelezett |
| döntési alternatívák: | $A$ | $B$ | $ A \land B \to S$ | |||||||||||
| 1. bíró véleménye | igen | nem | nem | |||||||||||
| 2. bíró véleménye | nem | igen | nem | |||||||||||
| 3. bíró véleménye | igen | igen | igen | |||||||||||
| közösségi vélemény (1) | igen | igen | – | |||||||||||
| közösségi vélemény (2) | – | – | nem | |||||||||||
| $A$ | – megengedhető a költségvetési hiány |
| $B$ | – az oktatásra többet kell költeni |
| $A\to B$ | – ha megengedhető a költségvetési hiány, akkor az oktatásra többet kell költeni |
| döntési alternatívák: | $A$ | $A \to B$ | $ B$ | |||||||||||
| 1. csoport véleménye | igen | igen | igen | |||||||||||
| 2. csoport véleménye | igen | nem | nem | |||||||||||
| 3. csoport véleménye | nem | igen | nem | |||||||||||
| közösségi vélemény (1) | igen | igen | – | |||||||||||
| közösségi vélemény (2) | – | – | nem | |||||||||||
Diszkurzív paradoxon, lehetetlenségi tétel
2002-ben Christian List és Philip Pettit a doktrinális paradoxon "belső logikáját" elemezve, és a problémát általánosítva bevezették a diszkurzív paradoxon fogalmát, majd megfogalmaztak egy lehetetlenségi tételt, amire azóta List-Pettit tételként hivatkoznak a szakirodalomban [Chris] A vizsgált szakterület is ekkortól kezdve kapott saját nevet, hiszen egyre inkább úgy hivatkoztak erre a vizsgálati irányra, mint a véleményaggregálás (judgement aggregation) elemzésével foglalkozó tudományterületre. Egy 2002-es cikkben List és Pettit Kornhauserék doktrinális paradoxonát értékelve rögtön bemutattak egy másik példát, amely a doktrinális paradoxont "kitermelő" élethelyzethez képest teljesen eltérő világból, a gazdaság területéről származott. Ezzel a kiterjesztéssel azt akarták szemléltetni, hogy az élet minden területén felbukkanhat a doktrinális paradoxonhoz hasonló jelenség. A példában szereplő kisvállalat dolgozóinak, akik egyben tulajdonosai is a cégnek, közösen kell dönteniük arról, lemondjanak-e fizetésük egy részéről annak érdekében, hogy egy biztonsági berendezést felszereljenek a cég telephelyén. Három szempontot mérlegelhet mindenki egyéni döntése során: (i) mennyire komoly az elhárítandó veszély, (ii) mennyire ígérkezik hatékonynak a berendezés, illetve (iii) személy szerint képes-e viselni a lemondás pénzügyi terheit. Ezek alapján – feltételezve, hogy hárman vesznek részt a döntésben – az alábbi táblázat szerint összegezhetjük az egyéni és közösségi döntéseket (itt is elég az igen vagy nem döntéseket feltüntetni).| \multirow{2}{*}{szempontok:} & komoly & hatékony & viselhető & \multirow{2}{*}{lemond-e}\\ | ||||||||||||||
| veszély | berendezés | anyagilag | ||||||||||||
| 1. személy véleménye | igen | nem | igen | nem | ||||||||||
| 2. személy véleménye | nem | igen | igen | nem | ||||||||||
| 3. személy véleménye | igen | igen | nem | nem | ||||||||||
| közösség véleménye (1) | igen | igen | igen | – | ||||||||||
| közösség véleménye (2) | – | – | – | nem | ||||||||||
$\concept{COMPLETE}(\Phi_i)\defi\forall i \forall k (\phi_k \in \Phi_i \lor \lnot \phi_k \in \Phi_i)$
teljes (hun) – complete (eng)
$\concept{CONSISTENT}(\Phi_i)\defi\forall i \forall k \lnot(\phi_k \in \Phi_i \land \lnot \phi_k \in \Phi_i)$
konzisztens (hun) – consistent (eng)
$\concept{DEDUCTIVELY\_CLOSED}(\Phi_i)\defi\forall i \forall k ( \Phi_i \vdash \phi_k \to \phi_k \in \Phi_i)$
deduktíve zárt (hun) – deductive closed (eng)
A teljességi feltétel szerint az $i.$ szavazó $\Phi_i$ véleményprofilja teljes, ha tartalmaz minden propozíciót vagy annak negáltját (akár mindkettőt). Ez a feltétel azt biztosítja, hogy mindenki állást foglaljon valahogy az adott véleménytér minden propozíciókettősével kapcsolatban, de ez az elvárás önmagában még nem eredményez racionális véleményprofilt, hiszen ez a kritérium "megengedi", hogy valaki egyszerre elfogadjon egy állítást és annak tagadását. Ezt "korrigálja" a konzisztenciakritérium, amely azt mondja ki, hogy az $i.$ szavazó $\Phi_i$ véleményprofilja akkor konzisztens, ha egy propozíció és annak negáltja közül csak az egyiket tartalmazza. [♦] Ez annyit jelent, hogy csak az ellentmondó állítások lehetőségét kizáró profilokat tartjuk racionális véleménynek. A deduktív zártság feltétele pedig azt "garantálja", hogy ha valamely $\phi_k$ propozíció logikailag levezethető a véleményprofilba tartozó propozíciókból, akkor a propozíció is beletartozik a véleményprofilba, azaz a szavazók egyénileg mind képesek levonni a logikailag szükséges következtetéseket. [♦] A három fenti tulajdonság alapján már megfogalmazhatjuk mind az egyéni, mind a csoport véleményprofilokra vonatkozó racionalitáskritériumot.$\concept{RATIONAL}(\Phi_i)\defi\concept{COMPLETE}(\Phi_i)\land \concept{CONSISTENT}(\Phi_i) \land \concept{DEDUCTIVELY\_CLOSED}(\Phi_i)$
egyénileg racionális (hun) – individually rational (eng)
Akkor beszélhetünk arról, hogy a $\Phi_i$ egyéni véleménykészlet (personal set of judgement) racionális, ha arra igaz, hogy teljes, konzisztens és deduktíve zárt. Az aggregált (csoportos, közösségi, kollektív) véleményprofilra vonatkozóan értelmét tekintve ugyanezt a racionalitáskritériumot követelhetjük meg, bár utána ki kell még egészítenünk azt valami mással is.$\concept{RATIONAL}(\Phi)\defi\concept{COMPLETE}(\Phi)\land \concept{CONSISTENT}(\Phi) \land \concept{DEDUCTIVELY\_CLOSED}(\Phi)$
csoportosan racionális (hun) – groups rational (eng)
A $\Phi$ csoportos véleménykészlet (collective set of judgement) racionalitásához szükséges feltételként kell megfogalmaznunk, hogy az legyen teljes, konzisztens és deduktíve zárt. Elégséges feltételként meg kell még fogalmaznunk azt az elvárást is, hogy az aggregáló függvénynek is racionálisnak kell lennie. Ehhez az univerzalitás (☜) és az anonimitás tulajdonságainak (☜) megkövetelésén túl egy további feltételt ki kell kötnünk, a szisztematikusság, szisztematicitás kritériumát. [♦]
$\concept{SYSTEMATIC}(\rel{F}(\Phi))\defi\forall \Phi, \Phi^{'} \in \mathbb{D}_F: \forall \phi, \psi \in X:(\forall i: \phi \in \Phi_i \leftrightarrow \psi \in \Phi_i^{'}) \to (\phi\in F(\Phi) \leftrightarrow $
$\psi \in F(\Phi_i^{'}))$
szisztematikus (hun) – systematic (eng)
Ez a kritérium az összegző függvényre vonatkozik. Az $\rel{F}(\Phi)$ függvényt akkor mondjuk szisztematikusnak, ha van két véleményprofilunk ($\Phi$ és $\Phi^{'}$), illetve két állításunk ($\phi$ és $\psi$), amelyekre igaz, hogy minden ($i.$) csoporttag esetén teljesül, hogy az egyik állítás akkor és csak akkor sorolható az egyik egyéni véleményprofilba ($\phi\in\Phi_i$), ha a másik vélemény a másik egyéni véleményprofilba ($\psi\in\Phi^{'}_i$) tartozik, akkor teljesülnie kell annak is, hogy a szóbanforgó két állítás beletartozik a két csoportos véleményprofilba is ($\phi\in\Phi$, illetve $\psi\in\Phi^{'}$). Csáji Balázs Csanád és Rédei Miklós a szisztemetikusság követelményét két tulajdonságra bontja fel.
"A szisztematicitás két tulajdonságot foglal magában:
1. Az, hogy a napirendnek egy bizonyos $\phi$ állítása igenelve van-e az összegezett véleményben, csak attól függ, hogy hogyan szavaztak a szavazók erre a $\phi$ napirendi pontra (és így nem függ attól, hogy a napirenden szereplő más állításokkal kapcsolatban ki hogyan szavazott).
2. Az a függvény, amely a $\phi$-re leadott N darab szavazat függvényében megadja, hogy $\phi$ el van-e fogadva az $F(\Phi)$ összesített véleményben, ugyanaz a függvény minden $\phi$ napirendi pont esetén."
[Csaji]
$\exists i(\lnot(\concept{RATIONAL}(\Phi)\land \concept{RATIONAL}(\Phi_i)\land \concept{UNIVERSAL}(\rel{F})\land \concept{ANONYM}(\rel{F})\land \concept{SYSTEMATIC}(\rel{F})))$
List-Pettit tétel (hun) – List-Pettit theorem (eng)
A List-Pettit tétel szerint nem létezik olyan $\rel{F}$ véleményaggregáló függvény, amely univerzális, anonim és szisztematikus, valamint minden racionális egyéni véleményprofilt racionális csoportos véleményprofillá összegez. Ez egy újabb lehetetlenségi tétel, csak most a racionalitásra vonatkozó intuitív elvárásaink a véleményaggregálás területére vonatkoztatva nem teljesül(het)nek. [♦] A tétel nagyon erőset állít, és úgy tűnhet, mintha a társadalmi gyakorlat nem is igazolná vissza az igazát. List és Pettit válasza erre az, hogy a ténylegesen létező, ebben az értelemben működőképes véleményösszegzési eljárások során mindig megsértünk valamilyen racionalitási elvet a fent definiáltak közül. Ha így van, akkor a következő fontos kérdés az lehet, hogy milyen módokon lehet enyhíteni a fenti elvárásokon, hogy még "vállalható" racionalitású és a megvalósíthatósági, lehetségességi elvárásoknak is megfelelő technikákat, eljárásokat kapjunk. [♦] Mark Pauly és Martin van Hess a List-Pettit tétel feltételeit az anonimitás elengedésével enyhítette, és következő fontos tételt tudta bebizonyítani [Pauly]$\forall i(\concept{RATIONAL}(\Phi)\land \concept{RATIONAL}(\Phi_i)\land \concept{UNIVERSAL}(\rel{F})\land \concept{SYSTEMATIC}(\rel{F}))\to \concept{DIC}(\rel{F})$
Pauly-van Hees tétel (hun) – Pauly-van Hees theorem (eng)
A Pauly-van Hees tétel azt mondja ki, hogy egy véleményösszegző függvény, amely kielégíti az univerzális értelmezési tartomány és a szisztematicitás feltételeit, akkor és csak akkor összegez racionális véleményprofilokat racionális csoportos véleményprofilba, ha a függvény diktatórikus. Már csak ezért is, de persze más okok miatt is, az (S4)-sémára szükség lesz a cselekvéselmélet tárgyalása során.